空间目标自适应光学图像椭圆部件检测

寇 鹏，智帅峰，程 耘，刘永祥*

（1.国防科技大学 电子科学学院,湖南 长沙 410073；2.西安卫星测控中心,陕西 西安 710600）

1 引言

随着光学成像技术的发展，特别是自适应光学成像技术的成熟，一定程度上解决了长期以来困扰空间目标成像的大气湍流问题，使空间目标高分辨率成像成为可能[1]。利用高分辨率自适应成像，可以提取空间目标的形状特征，对空间目标的实际尺寸形态进行估计，进一步分析空间目标及其部件结构。然而由于自适应成像尚未完全消除大气湍流等因素影响，造成目标轮廓模糊[2-3]。本文在对自适应光学图像进行复原和增强的基础上，通过一系列图像处理方法，检测在轨空间目标的椭圆型部件。

自适应图像中存在边缘杂乱、运动模糊、光照遮挡及湍流噪声等问题，如何高效准确地检测图像中的椭圆目标成为一个难题。现有常用的椭圆检测方法大致可分为3 大类：基于Hough变换（HT）、基于机器学习和基于边缘连接的方法。

基于HT 的椭圆检测是最常用的方法。HT椭圆检测的基本思想是将任意边缘像素投票到5D 参数空间。当累加器超过投票阈值时，将出现局部峰值，这意味着需要检测椭圆。但由于计算量大、内存消耗过多，直接将HT 应用在实际中几乎是不可行的。基于HT 的椭圆检测方法仍存在易受图像噪声和复杂背景的影响，且调整模型参数较为困难等问题[4-5]。基于机器学习的方法具有创新性，但由于人工标注昂贵，导致数据集获取相对困难，致使该类方法仍然不适合直接处理自适应光学图像[6-8]。

近年来，基于边缘连接的检测方法大大提高了椭圆检测性能。这类方法的主要问题是如何确定属于同一椭圆的椭圆弧。ELSD(Ellipse and Line Segment Detector)方法通过检测LS(Line Segments)和对LS 分组，充分利用了椭圆的梯度和几何特征，可以在不调整任何参数的情况下减少对各种类型图像的错检率[9]。文献[10]结合基于HT 和基于边缘链接的方法的优点来检测工业图像中的椭圆，但它们不适用于一般的椭圆检测。文献[11] 提出了一种弧段基于弧邻接矩阵的快速椭圆检测方法，但该方法对缺失椭圆的检测效果不够理想。文献[12] 提出了一种基于弧支撑线段(Arc-support Line Segments,ASLS)的椭圆检测方法，该方法能够精确高效检测出椭圆，尤其对有遮挡的椭圆检测较为理想。

本文首次将ASLS 方法引入空间目标自适应光学图像领域，针对ASLS 算法使用的Canny[13]等边缘提取算法弧段过分割的问题，提出了基于多尺度组合分组(Multiscale Combinatorial Grouping,MCG)的边缘提取算法[14]。针对ASLS 算法使用优度指标等验证方法存在部分虚假椭圆的情况，综合利用了优度、形状、位置、梯度和加权等几何特性约束较好地消除了虚假椭圆。

2 基于MCG 光学图像边缘提取

ASLS 方法使用Sobel 或Canny 等传统边缘检测算法提取图像中目标的边缘，Sobel 算法对噪声较多、灰度渐变的图像处理效果较好，但对边缘定位不是很准确且对灰度的变化不敏感；Canny 方法使用两种不同的阈值分别检测强边缘和弱边缘，该方法会尽可能多地标识出图像中的边缘，可能会将图像噪声标识为边缘。传统边缘提取算法对于自然图像能够取得较好的效果，但空间目标自适应光学图像具有目标暗弱、纹理复杂的特点，与普通的自然图像具有较大差别，使用传统边缘提取算法处理时常会出现自适应能力差且易出现伪边缘等问题。MCG 是一种自下而上的图像分层分割和目标建议生成相统一的边缘提取算法。MCG 首先开发了一种快速归一化分割策略，然后提出了一种有效利用多尺度信息的分层分段器，最后通过有效地探索多尺度信息空间组合，形成多尺度区域组合成图像边缘，对空间目标自适应光学图像边缘提取具有较好的效果，算法流程如图1 所示。

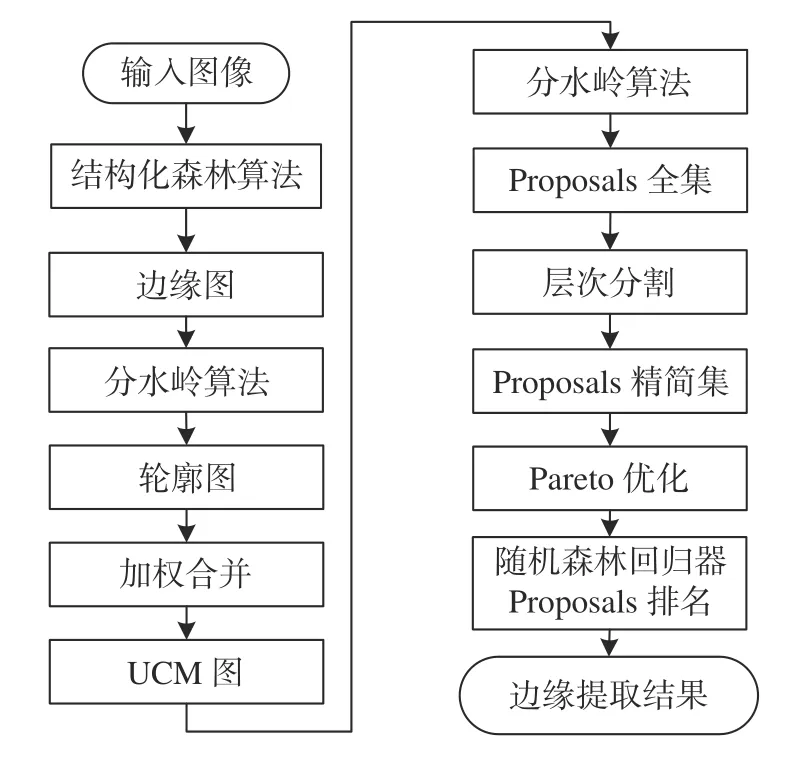
图1 MCG 算法流程图Fig.1 Flow chart of the MCG algorithm

MCG 算法首先使用结构化森林算法来产生“可能”的边缘图，即图像的像素点属于某边缘的概率。然后利于分水岭算法[15]对边缘图进行分界得到轮廓图，通过对轮廓图进行加权合并得到UCM(Ultrametric Contour Map)。在UCM 里通过白色线条分离黑色的连接区域，从而获取图像的N个连接区域，任意两个相邻区域之间都有一个差异度值。将N个叶子节点两两合并，得到N-1 个非叶子节点从而构造了一颗完全二叉树，二叉树的根部是整个图像区域，叶子节点是N个区域，这样一张UCM 图可以得到一个层次分割。初始的N个区域和组合后的非叶子节点可以认为是一个候选区域(Regional Proposal,RP)，一共是2N-1 个RP。然后使用Pareto 优化[16]得到多个自下而上的“单”、“双”、“三”和“四”共4 种RP，筛选覆盖率大于0.95 的RP，再进行孔洞填充。计算所有RP 的面积、周长、边界强度等特征，用这些特征训练随机森林回归器来对这些RP 排名，排名最高的即边界提取结果。图2 为实测Lacrosse4 卫星的自适应光学原始图像[17]、Sobel、Canny 和MCG 边缘检测图像。由图2 可知，MCG 边缘提取结果较Sobel 和Canny 结果具有伪边缘少和语义清晰等优点。

图2 空间目标自适应光学原始和边缘图像Fig.2 Adaptive optics original and edge images of space target

3 改进ASLS 算法的椭圆检测方法

图像中椭圆检测指标可使用准确率(P,Precision)、召回率(R,Recall)和F值(F-measure)来评价。P为检测出的正确椭圆个数与检测出的椭圆总数比值。R为检测出的正确椭圆个数与样本内所有正确椭圆个数的比值。P和R指标有时候会出现的矛盾的情况，可用P和R加权调和平均F值来综合评价：

重叠面积可作为评价椭圆准确率的重要指标，重叠面积表示检测出的椭圆面积与真实椭圆面积的比值。但重叠面积也有局限性，如两个重叠面积近似的椭圆可能位置不重合，因此，本文提出使用椭圆参数误差来评价两个椭圆的近似程度。如图3 所示，椭圆参数，即中心点的位置O(x,y)、方向角 φ、半长轴a和半短轴b，椭圆参数误差定义为检测得到椭圆参数与真值差的绝对值。

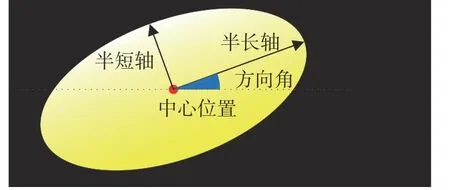
图3 椭圆参数定义Fig.3 Definition of ellipse parameters

3.1 ASLS 算法椭圆检测原理与流程

ASLS 定义为椭圆中一小段圆弧两个端点形成的“直线段”，但它不同于普通直线段，实际上是一小段弧，分布像曲线一样变化，只是局部近似为直线段[12]。弧支撑组(Arc-support Group,ASG)是具有相似几何特性的连续ASLS 连接形成的，每个ASG 同时被分配显著性分数。然后通过局部和全局方法将ASG 生成初始椭圆集，利用椭圆拟合的叠加原理和新的几何约束，即极性约束、区域约束和自适应内插准则，提高了算法的精度和效率。接着，根据椭圆中心、方向和半轴将5D椭圆参数空间分解为3 个子空间，并进行三阶段高效聚类。最后，通过优度度量和椭圆几何特性等约束剔除虚假椭圆，整个算法流程如图4 所示。

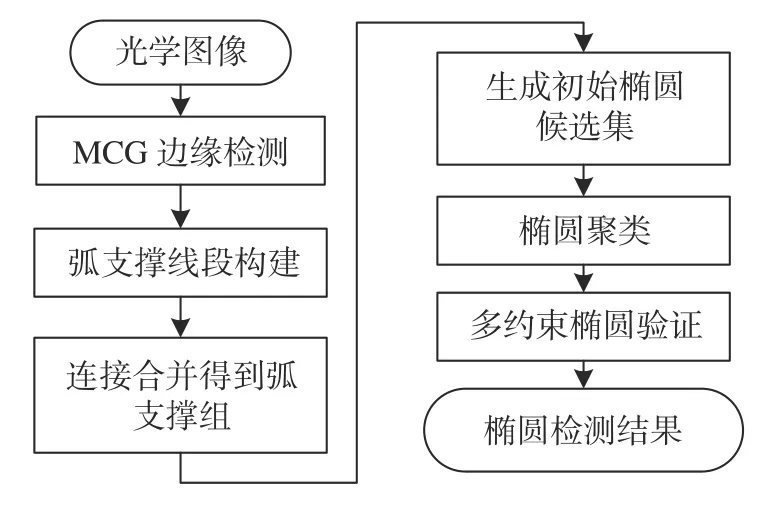
图4 改进ASLS 算法流程Fig.4 Flow chart of the improved ASLS algorithm

3.2 弧支撑组生成

与传统弧线段不同，ASLS 具有凸性，代表着椭圆弧的椭圆中心方向即弧支撑方向。满足连续性和凸性条件的ASLS 具有可链接性，连续性条件指一个ASLS 的头部与另一个ASLS 的尾部之间的距离应足够近。凸性条件指可连接的ASLS 均为顺时针或者逆时针。此外，为了避免在噪声的情况下出现错误的ASLS 链接，算法在当前ASLS 终点附近的局部统计区域内计算每个可能的下一个ASLS 的支撑点数量，并创建一个直方图，用于选择与当前ASLS 连接的统计数最大的ASLS。

3.3 生成初始椭圆候选集

考虑到一个ASG 可能包含一条曲线的所有ASLS，或仅包含一个独立的ASLS，因此使用阈值将显著度分数高的ASG 单独拟合到椭圆上和全局搜索所有有效的ASG 两种互补的方法来生成初始椭圆候选集，所有椭圆候选集应满足以下3 个约束：

(1)极性约束：观察椭圆边缘周围的图像区域后，椭圆的内部始终比外围亮或暗，其中亮表示ASLS 的极性为正，暗表示ASLS 的极性为负，通常同一个椭圆的极性也应该相同。

(2)区域约束：如果两个ASG 配对，则它们应位于相互有效区域中，区域约束表示为：

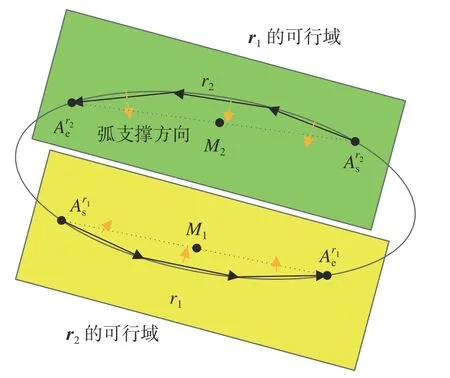
图5 两个弧支撑组生成候选椭圆Fig.5 Candidate ellipse generated by two arc-support groups

(3)自适应内边界约束：能够构成成对ASG的{r1,r2}的每个ASLS 的长度应该大于分割线段的总长度，即：

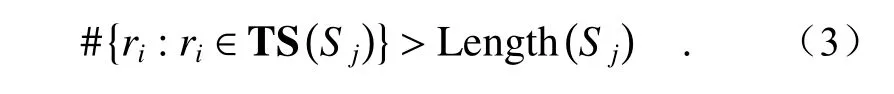
这里 TSS j表示ASLS 中S j的内边界集(j=1,2,···，Nr1+Nr2)，Nr1和Nr2分别为ASG 的r1和r2的数量。

3.4 椭圆聚类

聚类采用基于Mean Shift[18]的分层聚类方法，将5D 椭圆参数空间聚类分解为3 个低维级联空间的聚类，即中心O(x,y)i、方向角 φi和半轴(a,b)i。若初始椭圆集为Cinit共Minit个椭圆，则

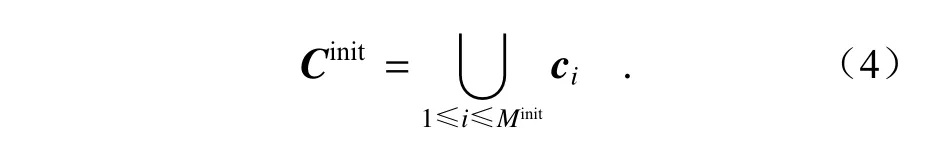
这里ci={(x,y)i,φi,(a,b)i}，即椭圆中心点、方向角和半轴。首先通过均值漂移有限迭代对椭圆中心进行聚类，然后再对方向角和半轴聚集，生成椭圆候选集Ec，可表示为

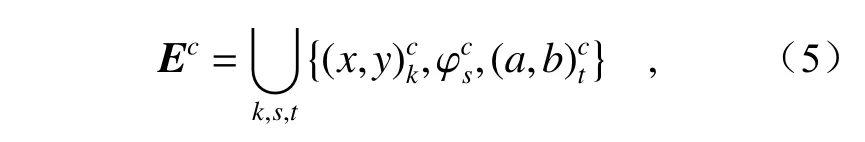
其中k,s,t分别表示中心，方向角和半轴个数。

3.5 椭圆候选验证

在进行椭圆候选验证时，在ASLS 算法所使用的优度等指标(Gd,Goodness)的基础上，结合AAMD[11](Arc Adjacency Matrix-Based Fast Ellipse Detection)思想，综合沿用了形状指标、位置指标、梯度指标和加权指标等约束，进一步提高了检测椭圆的质量。若候选椭圆由采样点集Ri,(i=1,2,···),Rv构成，采样点的采样方法是从拟合椭圆的极坐标出发，如果椭圆周长小于360，那么采样点个数就是周长，否则就采360 个点，即

φ为相对于椭圆长轴正向的角度，可以得到

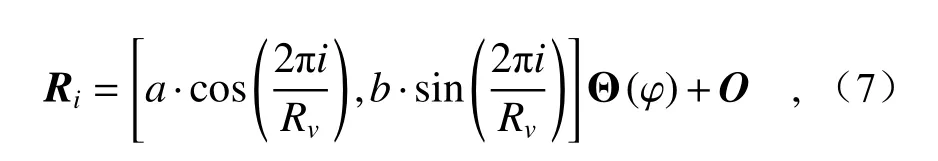
其中O为椭圆中心位置，Θ (φ)表示如下：

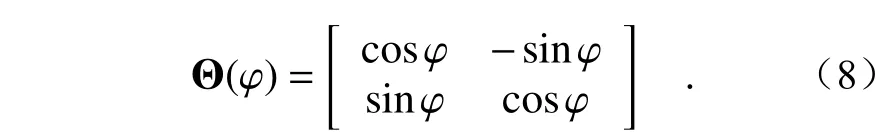
各项指标的计算公式如下：

（1）优度指标Gd。反映ASLS 数量和角度覆盖率，可用下面公式计算：

（2）形状指标HI。形状指标主要用于约束椭圆的几何形状，避免过小或过扁的椭圆。公式如下：

φarc是 一个阈值，一般取 π/3。约束主要由多√边形逼近椭圆的斜向像素距离最小值应大于推导得到，并根据实验结果调整了约束强弱程度。

（3）位置指标PI。如果第i个采样点Ri落在边缘点的一个8 邻域上，则认为其满足位置指标，对应指标值PIi=1，否则PIi=0。

（4）梯度指标VI。梯度指标用于验证当前采样点估计梯度Iξi和理论梯度gξi的差异，估计梯度可由有界正切误差估计[19]得出，理论梯度为，则梯度指标值为

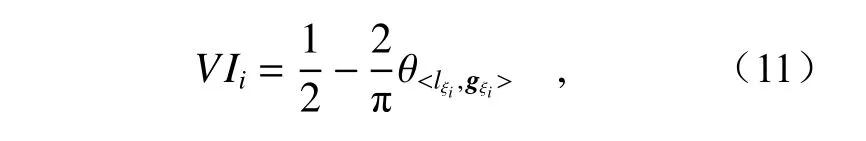
其中 ξi为第i个 采样点Ri的离心角，Θ(∗)的定义见式(8)，θ为Iξi和gξi夹角的锐角。

（5）加权指标。采样点是在极坐标下的角度均匀采样，从而导致采样点在图像上分布并不均匀，长轴两端点多，短轴两端点少，由此可以对每个采样点进行加权以提高椭圆验证精度。其中，每个采样点的加权指标为AIi=A(ξi)，则

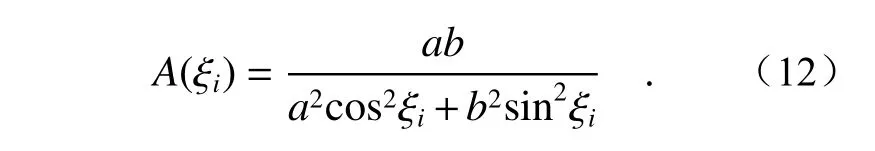
综合上述指标，可以用综合验证置信度Pe公式

得到所有候选椭圆的置信度，再通过门限去除置信度较低的椭圆。

4 实验与结果

实验使用空间目标的仿真和实测图像,验证了本文算法对空间目标自适应光学图像中椭圆部件检测的有效性和准确性。

4.1 边缘提取算法实验

实验的目的是验证不同边缘提取算法对不同类型光学图像边缘提取的效果。实验首先对自适应光学图像进行RL(Richardson-Lucy) 方法复原[20]，该方法具有不需要点扩散函数尺寸先验信息的优点和湍流退化模式的特点。然后分别采用Sobel、Prewitt、Canny 和MCG 算法提取复原后的图像边缘，边缘提取部分结果见图6。

图6(a)为原始目标自适应光学图像，图6(b)RL 为图像复原后的空间目标自适应光学图像，图6(c)～6(d)为实测Lacrosse4 卫星的光学图像[17]，图6(e)为实测Lacrosse2 卫星的光学图像[21]，图6(f)为实测哈勃太空望远镜光学图像[22]，图6(g)为实测国际空间站光学图像[23]。相比其它几种边缘提取算法，MCG 边缘提取算法边缘轮廓清晰，语义信息明确，且不容易受噪声干扰的优点。

4.2 椭圆检测结果

实验利用ELSDc[24]、AAMD、ASLS 和本文算法分别检测复原后的空间目标自适应光学图像中椭圆部件的个数和图像位置。算法实验平台主要参数为：Windows10 操作系统，PC 机(I7-8750H @2.2 GHz，16 GB RAM)，Matlab2016a 环境运行。为了检测出真实椭圆尤其是被遮挡的不完整椭圆，同时尽量减少虚假椭圆，实验中AAMD 算法参数设置为：曲线弯曲度为 π/3（该值越小，检测出的结果越像是一个圆），目标完整度比例为0.1（检测弧段与整个椭圆的最小比例）。ASLS 算法和本文算法参数设置为：完整度30°（检测弧段与整个椭圆的最小比例），边缘点数量比例系数0.2（检测点在整个椭圆的最小比例），无极性设置（极性正表示内白外黑，极性负表示内黑外白，无极性设置表示极性正负均检测），典型椭圆检测结果如图7（彩图见期刊电子版）所示。图中红色圆圈为检测出的置信度最高的若干个椭圆，椭圆参数误差结果见表1。

图7 空间目标自适应光学复原图像椭圆检测结果Fig.7 Ellipse detection results of adaptive optics restored images of partial space targets

表1 仿真图像椭圆参数平均误差Tab.1 Average error of linear structure components for test

ELSDc 算法检测平均误差非常高；对应仿真图像AAMD 和ASLS 算法存在一定的检测误差，尤其对实测图像检测误差仍然较高；除方向角外，本文算法检测的平均误差最小。

表2 给出了整个数据集算法的检测指标及平均耗时。在重叠面积门限为0.65 时，本文算法具有最高的准确率、召回率、F 值指标。图8 给出了不同重叠面积门限条件下各种算法的检测指标，本文算法均取得了最好的椭圆检测性能。本文算法的候选椭圆综合指标约束验证，能够有效剔除过扁及过小椭圆，因此准确率最高；同时MCG 边缘检测算法，能有效避免边缘过分割和语义信息不足的问题，因而召回率最高。但本文算法平均耗时最高，原因是MCG 边缘检测较经典的边缘检测算法步骤多速度慢，且对候选椭圆的综合指标验证计算时间相对较长。相比于传统椭圆检测算法，本文算法更适合在时效性要求不高的事后分析时应用。

表2 算法检测指标及平均耗时Tab.2 Average consumed times of those algorithms and the error detection rates

图8 重叠面积门限与检测指标关系Fig.8 Relationship between overlapping area threshold and detection index

5 结论

根据自适应光学图像纹理结构复杂及边缘模糊的特点，在对自适应光学图像进行图像复原的基础上，提出了基于改进ASLS 算法的空间目标椭圆部件的检测方法。不同于经典ASLS 方法使用传统算法提取边缘轮廓，该方法使用多尺度语义信息MCG 提取边缘轮廓，解决了传统边缘提取算法弧段过分割的问题。同时针对ASLS 算法使用优度指标等验证方法存在部分虚假椭圆的情况，综合利用了多种几何指标约束有效地消除了虚假椭圆。实验结果证明：椭圆检测中心点误差优于3 像素；半长轴误差优于4 像素；方向角误差优于3°；在重叠面积门限为0.65 时，本文算法的准确率为85.7%、召回率为93.3%和F 值为0.893，优于传统椭圆检测算法。本文算法在检测像素过少的小椭圆存在漏检现象，尤其是存在多个椭圆时的小椭圆检测效果较差，对过扁椭圆的检测效果也不够理想，同时本文算法时效性较差，后续将研究耗时较短且检测覆盖范围更全面的椭圆检测算法。

致谢：感谢北京航空航天大学图像处理中心李兆玺博士对本文工作的指导与支持。