基于卡尔曼滤波算法的精密数控加工方法
赵 铭 张 宇 贾志纲 马清涛
(太原科技大学 机械工程学院,太原 030024)
精密加工和超精密加工是机械制造中的重要领域,对尖端技术和国防工业的发展具有重要影响。确保零件加工精度的方案有两个方面:一种方案是靠机床自身的精度,制造超精密机床技术方面难度很大,且随着精度不断逼近极限,耗资越来越高,技术难度越来越大;另一种方案是误差补偿技术。
精密机床都装有在线检测系统,检测机床运动部件的位移位置,并有精密反馈闭环控制系统,以保证加工的尺寸精度[1]。然而,加工过程的热变形、切削液和削屑引起的震动、传感器的安置以及传感器的性能等,会导致在线检测数据包含一定频率的噪声干扰信号,造成在线监测获得的观测值出现偏差而影响误差补偿,影响加工精度。
卡尔曼滤波算法是当前热门的去噪声算法,广泛应用于导弹制导、无人驾驶以及机器人视觉定位等。分析精密机床自身加工误差规律和机床在线监测系统观测误差的规律,通过卡尔曼滤波算法对在线检测数值进行去噪处理,以获得工件加工状态的最优估计值,然后进行加工误差补偿。这种方法可以降低由于在线检测系统误差导致的加工误差,提高精密机床的加工精度。
1 加工方法
基于卡尔曼滤波算法的精密数控加工方法流程,如图1所示。针对当前检测系统中存在的不确定性噪声,采用卡尔曼滤波算法对所获的检测数据进行滤波处理,以获得零件实际加工过程中加工状态的最优估计值,随后数控机床反馈调节,补偿运动。
2 卡尔曼滤波算法模型构建
卡尔曼滤波(Kalman filtering)是利用线性动态系统状态方程,结合观测值和观测系统状态方程,计算获得系统状态最优估计值的算法[2]。由于存在不确定性精密数控加工过程,实际上是一个随机过程,即在线观测系统也存在不确定性,观测值也可以看作是一个随机过程。
一方面,研究精密数控机床的加工性能和在线检测系统的性能。刀具定位的误差噪声的波动服从高斯分布,确定噪声波动的方差,建立状态转移方程[3];在线检测系统获得的观测值与加工状态的真实值也存在误差噪声,噪声波动服从高斯分布,确定噪声的方差,建立观测方程。另一方面,根据工艺系统的状态转移方程和观测方程的参数建立卡尔曼滤波算法模型,对观测值进行降噪处理。
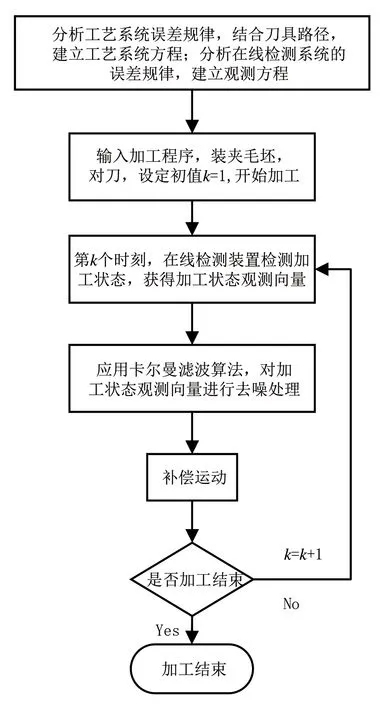
图1 基于卡尔曼滤波算法的精密数控加工方法流程图
2.1 建立工艺系统状态转移方程和观测方程
建立精密数控加工过程的离散系统模型,如图2所示。
反复检测误差出现的规律,分析其数值和方向,寻找规律,找出影响误差的主要因素,确定误差项目,并分析误差的期望值和方差。加工误差产生的原因一般包括原理误差、装夹误差、工艺系统精度及刀具磨损等[4]。
根据加工过程刀具路径和误差规律建立工艺系统方程,其中Mk为工艺系统状态向量,Hk、uk为状态转移矩阵,于是建立k-1时刻到k时刻的加工状态转移过程方程:
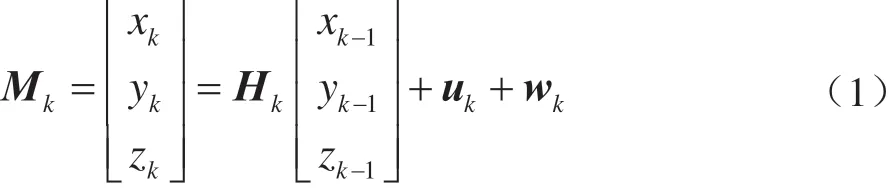
工艺系统噪声服从高斯分布:

分析在线观测系统的误差,找出其规律,在线观测系统的期望值和方差。检测值误差产生的原因一般包括加工过程的热变形、切削液和削屑引起的震动、传感器的安置以及传感器的性能。建立观测方程,Ak为在线检测系统获得的观测向量:
观测噪声vk服从高斯分布vk~N(0,Q)。
2.2 卡尔曼滤波算法对在线观测系统的观测值去噪处理
根据离散系统的参数,建立卡尔曼滤波算法模型,如图3所示。
对误差信号,应用卡尔曼滤波算法进行去噪声处理,获得加工状态的最优估计值。
通过卡尔曼滤波算法获得加工状态的最优估计值需要5步[5]。
(1)通过k-1时刻加工状态向量及系统方程计算k时刻工艺状态向量的预测值:
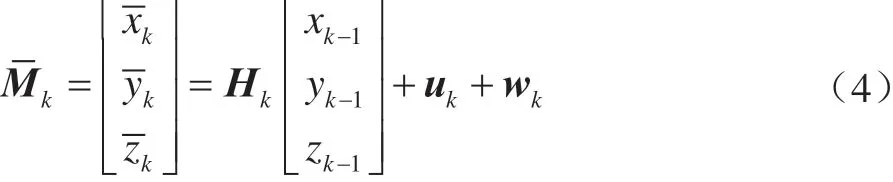
(2)协方差预测值:

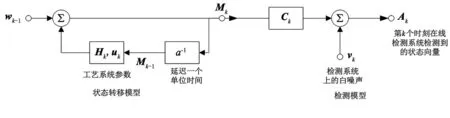
图2 离散系统模型

图3 卡尔曼滤波算法计算加工状态最优估计值模型
(3)卡尔曼增益:

(4)k时刻观测系统降低噪声后加工状态向量的最优估计值:
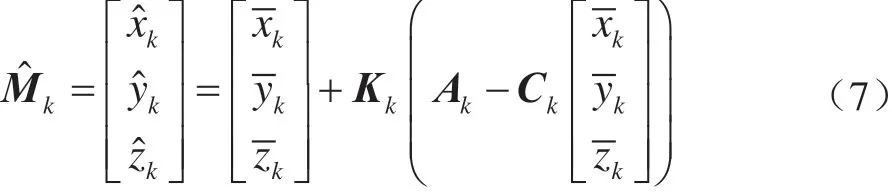
(5)k时刻协方差的最优估计值,用于下一个时刻计算:

闭环系统根据去噪后的观测向量也就是卡尔曼滤波算法的最优估计值作补偿运动。
3 仿真实验与结论
本文以直线度为衡量标准,精密加工直线度小于0.1 μm。为了验证通过卡尔曼滤波算法降噪后的检测值精度优于传统精密数控机床在线检测系统的检测值的精度,利用Matlab对这一问题进行仿真实验。
3.1 仿真实验
首先,建立离散系统方程。利用Matlab的随机数函数模拟未作补偿运动前的真实状态。加工状态波动k-1时刻和k时刻的关系为R(k)=R(k-1)+u,设置u~N(0,m),m=0.000 9,R(0)=0,生成50个加工状态真实值。
其次,观测系统的观测值G(k)=R(k)+v,设置v~N(0,n),n=0.000 4,在加工状态真实值的基础上生成50个观测值。
最后,设P(k)为卡尔曼滤波算法最优估计值,L(k)为协方差最优估计值,将卡尔曼滤波算法模型5个步骤简化为2个步骤:

设置P(1)=1,L(1)=0,k=1,2, ,50,应用Matlab编程进行递推运算获得加工状态的真实值,在线观测系统获得加工状态观测值,卡尔曼滤波算法计算获得加工状态最优估计值。
3.2 仿真结果与结论
通过仿真实验获得50个真实值(A1,A2, ,A50),在线检测系统获得的50个测量值(B1,B2, ,B50),50个卡尔曼(Kalman)滤波算法最优估计值(C1,C2, ,C50),一次仿真结果如图4所示。

图4 基于卡尔曼滤波算法的精密数控加工仿真结果
检测装置的精度可以通过检测噪声的方差体现。检测噪声方差越小,检测装置的精度越高。下面计算卡尔曼滤波最优估计值的噪声方差D(G)和检测值的噪声方差D(L)进行对比,分别为:

同样方法仿真5次,卡尔曼滤波最优估计值噪声与测量值噪声对比如表1所示。
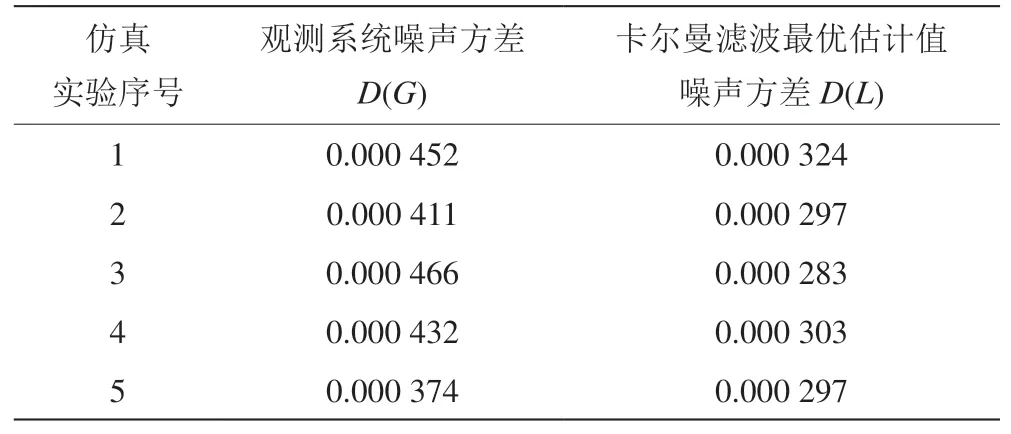
表1 卡尔曼滤波最优估计值噪声与测量值噪声对比
4 结语
由仿真实验可以看出,通过卡尔曼滤波算法对机床在线检测获得的检测数据进行去噪处理,卡尔曼最优估计值的噪声方差明显低于观测值的噪声方差。可见,通过卡尔曼滤波算法明显提高了在线检测系统的精度,提升了数控机床的加工精度。

