基于改进型随机共振的滚动轴承振动信号降噪方法研究
张羽薇 张春红* 赵 丹 刘广鑫
(1.沈阳航空航天大学,沈阳 110136;2.中国航发四川燃气涡轮研究院,成都 610500;3.空军装备部驻沈阳地区第一军事代表室,沈阳 110136)
作为双转子航空发动机的重要组成零件之一,滚动轴承工作状态的可靠性将影响发动机的安全运行。滚动轴承所处的环境中存在大量的噪声,极易对故障信号产生干扰,再加上故障信号的传输距离较远,故障信息的衰减严重,因此建立有效的信号增强模型可以有效分析信号[1]。
随机共振理论(Stochastic Resonance,SR)是由BENZI等提出的[2],能够从强噪声背景中有效提取微弱信号,在早期微弱特征信号的检测中应用广泛[3]。基于随机共振理论,MITAIN等提出了参数可调的自适应随机共振系统,通过调节噪声强度或改变随机共振系统的参数,使系统满足随机共振发生的条件,当输入微弱信号时,协同产生随机共振[4]。随着随机共振理论的成熟,许多学者利用随机共振理论进行航空发动机的故障检测。QIAO等提出了一种基于分段双稳态模型的自适应非饱和双稳态SR方法,用于机械故障的诊断[5]。LU等研究了一种基于全波信号构造策略的增强SR方法,并在轴承故障诊断中应用[6]。
基于上述理论,本文提出了一种基于改进型遗传算法对滚动轴承振动信号进行降噪处理。为验证所提出算法的有效性和可行性,将提出的方法应用于轴承实验信号的检测分析。结果表明,该方法能够有效降低噪声信号对故障信息的影响。
1 双稳态随机共振系统
1.1 随机共振原理
在信号分析中,噪声会干扰到有用信号的提取。但在特定的非线性系统中,噪声的存在可以与有用的周期信号共同作用,使得微弱信号被增强输出,此时的信号、噪声以及非线性随机系统产生的系统现象即随机共振。
1.2 振动信号双稳态系统
非线性系统一般存在两种状态,分别为稳定状态和非稳定状态。双稳态系统是指存在两个稳定状态的系统,是应用最为广泛的一类系统,其势函数为:
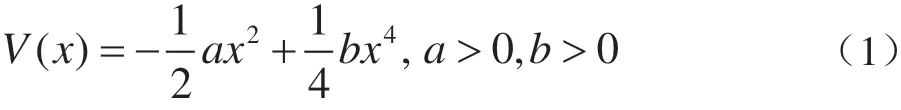
式中:V(x)为双稳态系统的势函数;x为系统的输出;a和b为系统的结构参数。
对于非线性系统而言,其非稳定状态为x=0,稳定状态时此时系统外界作用和噪声干扰,其势垒宽势垒高为∆V=a2/4b。
2 基于容忍的自适应遗传算法的建立
遗传算法(Genetic Algorithm,GA)是由John Holland提出的一种寻找最优解的方法。该算法可以在没有任何体系经验的条件下对参数进行二进制编码,并可以在多条路径下进行全局寻优。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
结合自适应遗传算法与容忍度的思想,提出一种容忍遗传算法。容忍遗传算法是将自适应的容忍适应度极限TFL增加或减去适应度波动的标准差,即针对遗传算法迭代的性能将变异概率Pm和交叉概率Pc的函数分段点分别进行不同的调整。
(1)初始化编码。采用经典二进制编码法对参数a和b进行编码初始化,并对参数a和b的阈值进行预测和估计。
(2)容忍遗传算子构建。遗传算子的建立对于优化效果具有重要意义。容忍遗传算子交叉概率为:
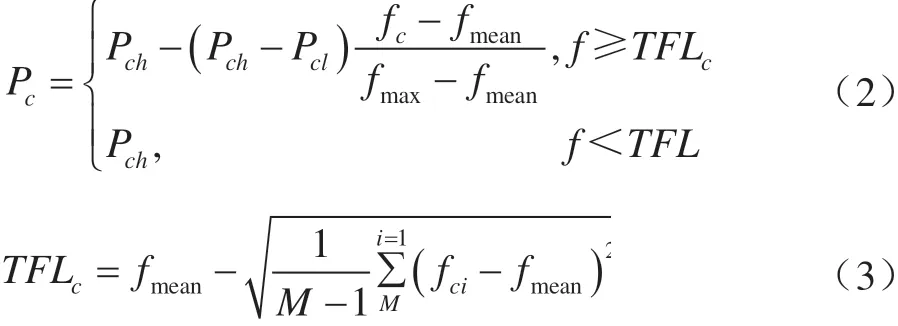
(3)选择适应度函数。采用改进的输出信噪比作为适应度函数,即:

SNRout表示输出信噪比,定义为:

式中:Sigpsd表示输出信号的功率谱密度;Nigpsd表示背景噪声的功率谱密度。
(4)终止条件。随着迭代次数的增加和个体的不断优化,当最优个体a和b的适应度值与平均适应度值的偏差d<10-6或者迭代次数达到预设的200代时,进化结束。
3 基于改进型随机共振的滚动轴承振动信号降噪方法
3.1 改进型随机共振系统模型
基于遗传算法基本思想,建立了一种基于容忍的自适应遗传算法随机共振模型。首先,对中介轴承的故障信号进行采集,包括故障部位的微弱特征信号和其他的噪声信号;其次,根据故障信号的信噪比构建适应度函数,建立GATA算法,之后利用GATA算法对系统的结构参数a和b进行自适应优化;最后,根据优化得到的结构参数a和b建立双稳态随机共振系统对故障信号进行信号增强处理,从而提取故障特征信息实现降噪。改进型随机共振算法原理图如图1所示。
3.2 实验验证
为了验证所提改进型随机共振模型的有效性和可行性,利用提出的模型对美国西储大学滚动轴承实验数据进行分析[7]。
本文验证所采用的轴承是6205-2RS JEM SKF深沟球轴承。采用线切割的方法在轴承的外圈制造了表面缺陷,外圈表面缺陷的尺寸直径为0.177 8 mm,深为0.279 4 mm。为了验证基于容忍遗传算法的自适应双稳态随机共振模型的有效性和可行性,在电机转速为1 797 r·min-1、12 000 Hz频率下采集轴承外圈故障特征信号,理论外圈故障频率为66.0 Hz,高压转子转频为5.0 Hz,低压转子转频为10.0 Hz。时域信号中存在一定的冲击成分,但是没有规律可言,主要是因为外部的噪声信号将故障信号掩盖,导致冲击的周期性并不明显。故障信息大多存在于0~2 000 Hz,在高频部分存在峰值,在低频部分峰值杂乱,无法有效提取故障特征频率。
利用基于改进型随机共振系统对结构参数a和b进行优化处理,设定双稳态随机共振的结构参数的可行域分别为a∈(0,10 000],b∈(0,10 000],最大的迭代次数为2 000,最终获得的最优结构参数为a=0.838,b=7 223.61。
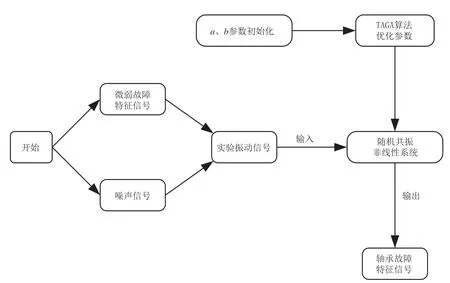
图1 改进型随机共振原理图
经过随机共振处理的故障信号滤掉了大量高能量噪声,冲击成分更具周期性且峰值更趋稳定,故障信号在低频区域更加密集和明显。随机共振不仅过滤掉了大量的高频噪声信号,而且削减了低频区域冗余的噪声信号能量,放大了低频区域的故障信号,使得故障信息更加明显,包络谱频率成分清晰。在降噪之前的振动信号中,噪声信号能量过大,掩盖了故障信号,导致故障特征频率提取产生误差,远不及降噪后的故障冲击明显。通过降噪前后的信号特征可见,提出的改进型随机共振算法增强了故障信号的冲击特性,实现了中介轴承振动信号的有效降噪。
4 结语
通过研究双稳态随机共振的机理,在传统的自适应遗传算法中融合容忍度思想,建立了基于容忍的自适应双稳态随机共振模型。采用改进型随机振动算法来降低噪声信号对故障信息的影响,并通过实验数据进行验证,处理了滚动轴承的外圈故障,得到了良好的效果,验证了该算法的可行性与可靠性。

