基于主成分分析与K近邻分类算法的化工干燥分类模型

张婷暄，邓久宁，汪洁，孙怀宇

（沈阳化工大学化学工程学院，辽宁 沈阳 110142）

流化床干燥过程是一个复杂的过程，原因之一是流化床内部是动态流动、传热和传质的过程，而不是一个稳态的过程。正是由于过程的复杂性，单纯从机理出发的模拟难于解决实际流程中的问题。基于大数据分析的模型建立及人流化床干燥过程是一个复杂的过程，原因之一是流化床内部是动态流动、传热和传质的过程，而不是一个稳态的过程。正是由于过程的复杂性，单纯从机理出发的模拟难于解决实际流程中的问题。工智能是一种有效的方式。对于传统化工的流程工业领域来说，人工智能与其融合度较低，仍然存在较大的发展空间[1]。

PVC 流化床干燥器是生产中重要的一个干燥设备。湿物料以流体的形式被输送到流化床干燥其中，在流化床干燥器内部进行干燥操作。由于测温点只存在于固定的几个位置，所以如果在产品干燥结束后发现产品含水量不合格，那就会增加成本。这时如果有可以实时监控产品含水量的设备，那就会在产品干燥结束前发现不合格的产品，从而进行继续干燥，这样可以节省很多时间和成本。

本文试通过于实际生产数据的分析，得到较准确的数据驱动模型。主要解决了下述问题：现场得到的数据中存在一些意外及缺失数据，影响数据分析的进行。本文通过使用KNN 的思想，采用python 3.0 的sklearn 库中的KNNImputer 方法，对异常值进行填充；由于物料在干燥器中的流动，使得不同位置的数据变化存在时间上的先后次序影响。本文通过计算不同测温点和产品出口处的含水量的相关性系数，来确定最佳的时间间隔，从而消除时间的影响；实际的测量点较多，文章通过主成分分析法（PCA）进行降维，简化了数据的特征，并在此基础上进行了分类模型的构建。

本文通过数据预处理，找出每个测温点到产品出口的时间长度，构建同一物料在不同时间不同测温点的数据表格，随后将主成分分析法（PCA）和K 近邻分类算法（KNN）相结合，构造实时监测的分类模型。

1 基于主成分分析法（PCA）的K 近邻（KNN）分类模型的设计

1.1 KNN 算法填充异常值的描述

常见的缺失值填充的方法有以下几种方法：固定值填充、均值填充、众数填充、中位数填充、上下数据填充、插值法填充等。这些常见的填补异常值的方法，虽然可以对大部分数据集进行填充，但是对于个别数据波动较大的数据集来说，这些填充进去的数据不会很精确[3-4]。而通过KNN 算法填充时根据邻近的多个“邻居”来计算所需填充的异常值，会让计算得到的填充值更为贴近邻近的数据，让得到的数据相对于上述方式得到的数据更加精准，所以本文采用 KNN 算法来对异常值进行填充。KNNImputer 方法的思想是找到数据空间中距离最近的K 个样本，然后通过这K 个样本来估计缺失数据点的值。缺失值可以用K 个相邻样本点的均值、中位数、众数或者常数进行填充。KNNImputer 预测的步骤是选择其他不存在缺失值的列，同时去除需要预测缺失值的行和列，然后计算欧氏距离找到K 个近邻点。如果是离散的缺失值，则使用KNN分类器，投票选出K 个邻居中最多的类别进行填补；如果是连续的变量，则用KNN 回归器，使用K 个邻居的平均值进行填补[7]。

1.2 主成分分析法（PCA）描述

主成分分析法（PCA）是一种用于探索高维数据的技术。PCA 通常用于高维数据集的探索与可视化。还可以用于数据压缩，数据预处理等。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。PCA 的基本思想如下：将具有一定相关性的多个原始变量，通过组合变换，得到一组互相无关的综合变量。从中选取几个较少的能够在很大程度上反映原始变量信息的综合变量，就是主成分，新的低维数据集会尽可能地保留原始数据的变量，可以将高维数据集映射到低维空间的同时，尽可能地保留更多变量。主成分之间是互不相关的，且是原始变量的线性组合[1]。

1.3 K 近邻（KNN）分类算法的描述

K 近邻算法的核心思想是：如果一个实例在特征空间中的K 个最相似（即特征空间中最近邻）的实例中的大多数属于某一个类别，则该实例也属于这个类别。所选择的邻居都是已经正确分类的实例。

该算法假定所有的实例对应于N 维欧式空间中的点。通过计算一个点与其他所有点之间的距离，取出与该点最近的K 个点，然后统计这K 个点里面所属分类比例最大的，则这个点属于该分类[1-2]。该算法涉及3 个主要因素：实例集、距离或相似的衡量、K 的大小。

KNN 算法的实现就是取决于，未知样本和训练样本的“距离”。而计算“距离”可以利用欧式距离算法，如式（1）：

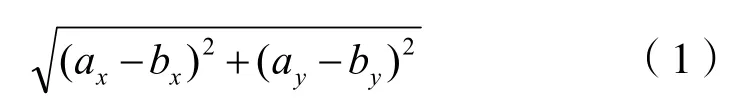
1.4 基于PCA 的KNN 分类模型的实现方案

1）获取工厂实际数据，整理数据，对数据进行预处理。

2）数据清洗。数据清洗是一项复杂且繁琐的工作，同时也是整个数据分析过程中最为重要的环节。实际的工作中确实如此，数据清洗的目的有两个，第一是通过清洗让数据可用。第二是让数据变得更适合进行后续的分析工作[5]。本文通过箱线图四分位方法计算得到异常值，并通过KNN 算法计算得到的数据对异常值进行替换，从而完成数据清洗的工作。

3）通过python3.0 的内置函数计算相关系数，通过相关性系数的大小来寻找时间步长。由于工厂操作人员给出整个流程时间不超过120 min，所以通过循环，从时间间隔为0 到120 进行循环计算，找出相关性最高的对应的时间长度，此时的时间长度就是最佳的时间间隔。随后再在经过预处理的数据文件上减去时间步长，将数据处理成为同一流股物料在不同测温点时对应的数据。

4）由于实际数据的特征有10 个，和一个干燥后的产品的含水量。所以本文通过主成分分析法（PCA）对数据进行操作。通过python3.0 的sklearn库来调用PCA 方法，并做出降维时保留90%的数据信息的限制。通过PCA，既可以减少数据的特征值的个数，又可以极大的保留最大程度地数据信息，不会因为降维，使数据信息丢失很多。

5）经过PCA 降维后的数据，通过调用sklearn库的train_test_split 方法将他们划分训练集与测试集，用来训练KNN 分类模型。其中训练集占比80%，测试集占比20%。

6）划分好训练集与测试集后，将训练集给KNN模型进行训练，通过对训练集的训练，构造KNN模型。

7）通过测试集来验证训练的KNN 模型的准确率。

2 数据预处理

2.1 实验平台描述

通过Anaconda3.0 自带的Jupyter Notebook 中的python3.0 进行实验。

2.2 获取数据

数据是由工厂现场的数据文件获得的。由于温度对于含水量的影响是最大的，本次分析主要对温度测量值进行分析。其中测温点有 10 个。而AIA2203.PV 为产品的含水量。样本包括了1 440 个时间点的数据。

2.3 数据清洗

1）判断数据中的异常值

通过箱线图四分位方法计算，此方法可用于识别一组数据中的异常值。具体方法如下：

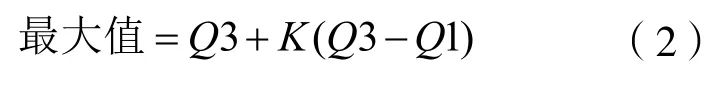
式中：Q3—上四分位数；

Q1—下四分位数；

K—代表系数，可以取值1.5。

在最大值最小值之间的值就是可接受范围内的数值，这两个值之外的数认为是异常值[6]。

2）异常值填充

这里选择用KNN 算法对异常的数据进行填充，使用Sklearn 中的KNNImputer 方法[8]对缺失值进行填充，这个基于KNN 算法的新方法使得我们现在可以更便捷地处理缺失值，并且与直接用均值、中位数相比更为可靠。利用“近朱者赤”的KNN 算法原理，这种插补方法借助其他特征的分布来对目标特征进行缺失值填充。

表1 各工位异常值个数表

2.4 寻找最优时间间隔

由于流化床干燥过程属于过程工艺，所以是持续作业。也正是由于流动，所以测温点每次读取的数据，都不是同一物料对应的温度，这就导致在同一时刻读取的产品含水量和产品在干燥时的温度并不是对应的。为了解决这个问题，就要找到某一微元物料在不同测温点距离到产品干燥结束时的时间间隔。在考虑时间间隔后，这时每条的数据才是同一微元物料在不同测温点的数据信息，也才与最终的含水量相关[9-10]。

通过工厂现场的数据得知，整个干燥流程不超过2 h，所以采用了逐步计算不同测温点在不同时间长度下（2 h 内）的相关性系数，寻找相关性最大时对应的时间差，以此来判断不同测温点距离产品出口的时间间隔。通过自定义函数里采用循环来执行此计算过程。最后得到的时间差如表2。

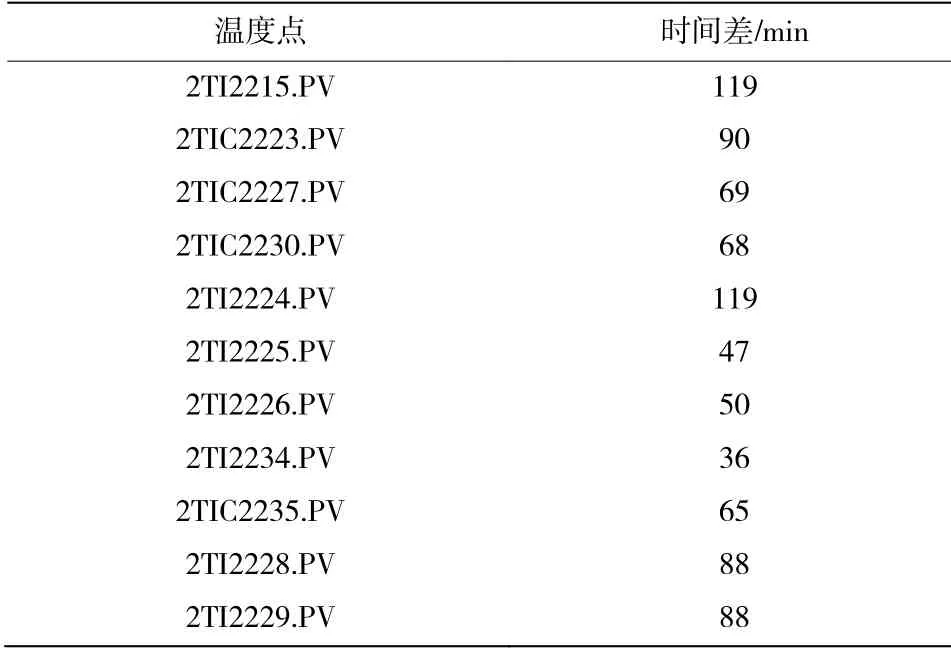
表2 各个测温点与产品含水量之间最佳时间差

3 模型的建立

3.1 通过主成分分析法（PCA）对数据降维

通过调用sklearn 库中的PCA 方法，对数据进行降维。在降维时，规定保留90%的数据信息，使数据在降维时较少的损失数据信息。其中，表3为降维后的主成分部分特征数据；表4为主成分的方差贡献率。

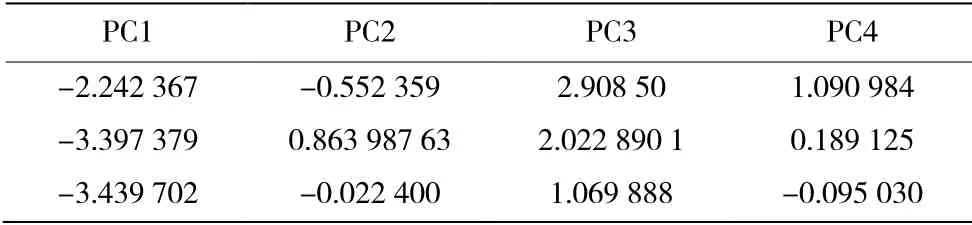
表3 降维后的主成分部分特征数据

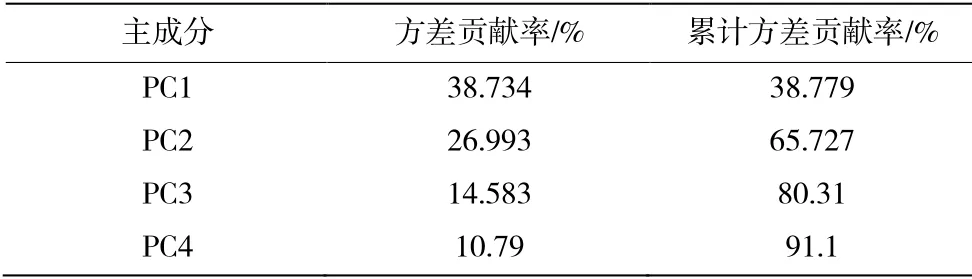
表4 主成分的方差贡献率

根据上表可知，经过PCA 降维，降成了4 个维度，而这四个维度的数据信息包含了91.1%的原始数据信息。所以选择这4 个主成分进行构建KNN分类模型。含水量合格情况计数表见表5。

表5 含水量合格情况计数表

3.2 划分训练集与测试集

通过调用sklearn 库的train_test_split 方法来进行训练集与测试集的划分。把新构建的数据集new_X 中经过PCA 降维后得到的4 个主成分PC1，PC2，PC3，PC4 对应的数据作为X，将新构建的数据集new_X 中的产品是否合格对应的数据作为Y。分别对X 和Y 进行划分为X_train，X_test，Y_train，Y_test。分别对应X 与Y 的训练集与测试集。。

3.3 训练KNN 分类模型

通过调用sklearn 库中的KNN 方法，对划分好的训练集X_train，Y_train 进行训练，得到一个KNN分类模型。

3.4 验证模型的精确度

根据式4 计算KNN 分类模型的预测准确率为87.547%，可以认为该训练模型拥有较好的分类准确率，可以用于实时监测产品的含水量。

4 结 论

本文在数据清洗时，使用KNN 算法对异常值进行填充，随后将主成分分析法（PCA）和K 近邻分类算法（KNN）相结合，构造了一个基于低维度数据的同时，保留了90%的数据信息的分类模型。可以极大地减少基于机理的化工建模计算中的复杂信息，大大地提高了计算效率。同时，建立的分类模型的准确率高达87.547%，是拥有不错的分类能力的一类模型。而且由于很多温度点的变化时刻早于含水量的变化时刻，从而可能构建在线的预测监视系统，及时对于生产条件进行调整。本文还存在一些不足。例如在考虑测温点距离产品出口的时间长度时，采用的是计算相关值来确定的时间，并未考虑到变化在时间轴上的发散。同时，本文是基于数据驱动进行的分析，还没有更多地应用化工过程的机理进行支持。在后续的研究中会考虑加入化工方面的机理建模，将两者结合起来，以期得到更好的模型。