在思维结构的突破中促使学习发生
陈六一
一、单点唤醒
学生在学习新知识时,一般都是从他原有的思维结构出发,以“旧知”来解释“新知”。所以几乎所有的认知理论,都强调学生的数学现实会对当前的数学学习产生作用。徐老师深谙理论,通过唤醒学生对小数意义、性质等单点知识的理解,使其自然地通向多点知识的融通。
【教学片段1】
師:本学期我们接触到的最多的知识是什么?
生:小数。
师:我们学过了小数的哪些知识?
生:加、减、乘、除。
师:这是四则运算。
生:还有小数的性质。小数的简便计算。
师:除了计算,还学过小数的什么?
生:近似数。
师:学习小数的性质之前学了什么?
生:小数的意义。
师:对呀,小数是怎么产生的呢?
生:和分数、整数有关。在数学中产生,也在生活中产生。
师:的确,整数不够用了,产生了分数、小数,小数能精准地表达。
生:十进分数可以用小数表示。
师:讲得好,那接下来大家在作业单中,画图表示一些小数。
生:整数1,平均分成10份,其中一份用分数表示是十分之一,写成小数是0.1;平均分成100份,其中一份用分数表示是一百分之一,写成小数是0.01;平均分成1000份,其中一份用分数表示是一千分之一,写成小数是0.001。
【赏析】透过教学片段可以看出,凭借着回忆,学生大多对小数概念只是具备单点状理解,还不能将多点知识进行关联,进而领悟到每一个知识点都指向核心概念——计数单位。而这,正是复习课的教学任务所在。所以徐老师一边让学生尽情地说,一边将学生的思维聚焦到核心概念。
二、多点关联
基于片段1的教学,可以看见学生心中的小数缺乏系统性与整体性,这样的小数知识只是小数的实然状态,需要通过释然加以结构化,以达到小数与整数的一致性同构。这样,学生在思考“新知”与“旧知”不是一回事的失衡中,重新平衡到“新知”与“旧知”就是一回事。同时,因为有了思维的参与,“新知”的框架不但被扩充,也被改良。
【教学片段2】
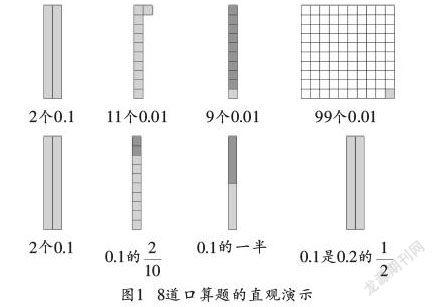
徐老师出示8道口算题:0.1+0.1,0.1+0.01,0.1-0.01,1-0.01,0.1×2,0.1×0.2,0.1÷2,0.1÷0.2。学生独立完成。
师:能用计数单位的知识来解释计算吗?
生:①0.1+0.1,2个十分之一,是十分之二,就是0.2。②2个0.1就是0.2。③0.1+0.01,1个十分之一加1个一百分之一,是11个0.01,是0.11。④0.1-0.01,1个0.1是10个0.01,10个0.01减去1个0.01,得9个0.01。⑤1-0.01,1等于100个0.01,100个0.01减去1个0.01,得到99个0.01,是0.99。⑥0.1×2,表示2个0.1相加,是0.2。⑦0.1×0.2,0.1的十分之二,得2个0.01,是0.02。⑧0.1÷2,十分之一的一半,0.05。⑨0.1÷0.2,被除数、除数同时扩大10倍,也就是1÷2,商是0.5。
师:是不是可以想0.1里有几个0.2?
生:半个,是0.5。
以上学生回答时,徐老师同步出示课件,如图1。
师:会笔算吗?带着下面4个问题进行计算:①计算小数加减要注意些什么?②小数乘法积的小数点位置如何确定?③除数是小数为什么要化为整数?④小数四则运算中哪些地方运用了小数性质?
徐老师出示笔算题:3.8+1.2,5-3.8,3.8×1.2,4.56÷3.8。
生:3.8+1.2=5,5-3.8=1.2。
师:做5-3.8,被减数5为什么要添一个小数点和0?根据什么理由添0的?
生:根据小数的性质,在小数的末尾添上0,小数的大小不变,添上0,就使得被减数的十分位和减数的十分位上都有了数,方便计算。
师:回到问题①,小数加减法要注意什么呢?
生:小数点对齐。
师:为什么要小数点对齐?
生:数位对齐,计数单位相同。
生:3.8×1.2,两个乘数先当做整数,然后把积缩小100倍,或者数出两位小数。
生:4.56÷3.8,变成45.6÷38,得数1.2。
生:小数乘除法,先将小数转化成整数,除的时候依据的是商不变规律,乘的时候依据的是积的变化规律。
师:总结回顾,不管是做加减法时小数点对齐,还是做乘除法时转化成整数,都和计数单位有关系。
师:哪些地方用了小数的性质?
生:加法结果的化简,减法小数末尾添0……
师:今后学什么呢?可能和什么有关系?
生:分数四则运算,大概和分数单位有关。
【赏析】片段2中的教学,徐老师让学生在口算中,感悟到了小数加减乘除其实和之前学习的整数四则运算一样,算的都是计数单位;在笔算中,学生再一次体验了数位对齐是为了把相同的计数单位进行加减,转化成整数得到积与商也是为了数出计数单位。学生充分的说理,说明了他们已经将多个知识点进行了关联,并一致联结到“计数单位”,于是小数的加减乘除做的其实还是整数的加减乘除,只要再走一步,接着去数有多少个计数单位。
三、拓展结构
教学的路径是线性的,但学生在教师的引领下,参透数学本质的过程是迂回的。徐老师的追问,学生自我突破瓶颈时产生的疑惑,都会将学生带到“失败”与“挫折”面前。但是,走出“失败”与“挫折”,学生便能举一反三,将错误问题的解决变成实实在在的思维实验,于是学生的认知获得进一步拓展,许多看上去的不同都找到了相同的原理。例如,解释3.8×1.2的算理,学生认识大多停留在将小数当成整数,积有两位小数,追问“为什么积是两位小数”,学生一般不会联系到计数单位。计算算的是相同计数单位,而算是快速地数,所以计算也可以纳入“数是数出来的”认知结构,学生算3.8×1.2就是数38×12个0.01,于此认知结构与数学结构同步丰盈。
【教学片段3】
师:根据38×12=456直接写得数,不计算,带着找规律的眼光来思考。
生:①3.8×12,結果是456个0.1,也就等于45.6。②0.38×12,结果是456个0.01,也就等于4.56。③0.38×1.2,结果是456个0.001,也就等于0.456。④0.38×0.12,结果是456个0.0001,也就等于0.0456。
师:自己再出两题。
生:0.038×12,结果是456个0.001,也就等于0.456。
生:我能出一个和你答案一样的算式,0.0038×120,结果也是456个0.001。
生:这些题目在讲同一个数学故事,都是数456个不同的计数单位。
师:根据4.56÷3.8=1.2,填上合适的数,45.6÷(?摇?摇?摇?摇?摇?摇)=1.2,0.456÷( )=1.2,( )÷380=1.2,( )÷0.038=1.2。
【赏析】徐老师在复习乘除法时,花了更多的时间,让思维有了更多的“挣扎”。由此,学生也能体会到运算的背后有着运算律的支撑。例如,学生说的“0.38×1.2,结果是456个0.001,也就等于0.456”,这是多次利用了乘法交换律和结合律,具体过程是:0.38×1.2=(38×0.01)×(12×0.1)=(38×12)×(0.01×0.1)=456×0.001=0.456。在此,也可以看到小数乘法运算中还有一个难点就是理解两个小数相乘,其结果的计数单位对于原来的两个乘数已经发生了变化,一如0.38×1.2中,0.38数的是38个0.01,1.2数的是12个0.1,两数相乘,数的是0.01×0.1即0.001这个计数单位。而这也提醒我们小数认识的教学要放在整体视野中考量,其意义要突出小数是不断“十分”的产物,如0.01是0.1十分后,数出其中1份的数,0.001是0.01十分后,数出其中1份的数……
纵观全课,徐老师从学生的数学现实发端教学,根据学生学习进程中的表现,做出了单点结构(教学片段1)、多点结构(教学片段2)、拓展结构(教学片段3)的诊断评价,然后分三个环节依次逐级提升学生的理解水平:学生一开始只有关于小数的单个知识点,接着徐老师引导串联知识点,以核心概念“计数单位”统领学习,最后学生在现象的一致性中,抽象出小数的四则运算同整数四则运算一样,都是依据运算律数计数单位的个数。三次教师的教,也是三次学生的学,我们看见了学生知识结构维度、认知结构维度在增长,面对思维的挑战也逐渐组织得有序有理。
(作者单位:南京师范大学苏州实验学校?摇?摇?摇责任编辑:王彬)

