基于二维双树复小波变换的无人机个体识别*

罗正华，李 霞，杨耀如，向 博，罗晓笛

(1.成都大学 电子信息与电气工程学院,成都 610106；2.电信科学技术第五研究所，成都 610062)

0 引 言

反无人机技术是各国关注的重点技术，其中，“非合作型”无人机个体识别是反无人机技术的重点和难点[1]。目前，针对“非合作型”无人机个体识别主要是借鉴辐射源个体识别方法，通过对信号进行分析测量，提取出反映目标身份的“指纹特征”，将其与特征库比对，从而确定目标身份[2]。

双谱分析法是处理非高斯信号的主要数学工具，能够在保留信号的幅度和相位信息的同时自动抑制高斯噪声，故被广泛应用于特征提取[3]。无人机图传信号为非高斯信号[4]，故双谱分析法适用于无人机图传信号的处理，但直接将双谱作为特征进行无人机分类，存在数据维数高和计算复杂的问题，需要进行二次特征提取。文献[5]采用矩形积分法实现特征降维，文献[6]利用 Fisher类测度选出最具目标分辨能力的若干双谱特征，文献[7]提取双谱的平坦度、谱亮度和谱滚降度三类谱特征组成特征向量实现数据降维，文献[8]提取双谱幅度特征、矩特征和加权中心三个特征实现降维，文献[9]利用灰度共生矩阵提取双谱三维图像纹理特征：这些算法均有效地实现了双谱的二次特征提取。

二维双树复小波变换(Two-dimensional Dual-tree Complex Wavelet Transform，2D_DTCWT)是图像纹理特征提取的常用算法[10]。它的实现只需对4个二维可分离小波变换的对应子带进行加减操作，效率较高容易实施，且具有方向选择性和良好的时频局部化的分析能力。基于上述特点，本文提出基于二维双树复小波变换的双谱二次特征提取算法，用该算法对无人机图传信号双谱的进行分解，高效地将维度较高的双谱值转换为维数较低的图像纹理特征，实现双谱二次特征提取，再将其作为无人机的“指纹特征”实现无人机个体识别。

1 无人机信号非线性模型

在采用无源探测技术对民用微型无人机实现监管过程中，对于“非合作型”无人机，先验信息少，难以通过参数信息完成无人机型号的识别。无人机图传信号是由采集的视频数据进行前期处理，再经射频放大电路放大发射出去的。射频放大电路主要由射频功率放大器组成，故可借鉴辐射源个体识别方法，通过对无人机图传信号进行双谱分析，提取出与功率放大器的非线性特性相对应的指纹特征来标记每一台无人机。

由于制造工艺的限制和器件的随机性，功率放大器的理想线性增益特性变成了非线性，即使是同型号、同批次的功率放大器的增益也不尽相同，这便构成了信号的“指纹特征”。功率放大器的非线性特性作用于发射信号后产生互调频率、谐波频率以及一些交叉调制、寄生调制等杂散成分[11]。为研究此类“指纹特征”，需要对功率放大器进行建模来表征其工作特性。本文采用广泛使用的Taylor 级数模型对功率放大器进行建模[12]，如式(1)所示:

(1)

式中：an表示功率放大器Taylor模型的第n阶参数，x(t)为输入信号，y(t)为输出信号。an的不同将导致功率放大器增益效果的不同。

2 基于2D_DTCWT的无人机个体识别算法

2.1 算法流程

本文算法总体流程如图1所示。首先，将接收到的无人机图传信号进行预处理并用非参数法高阶谱估计方法估计其双谱；然后，利用2D_DTCWT算法对双谱图进行分解，从而得到双谱图在不同方向和不同尺度上的纹理特征图，由这些图像的能量和能量偏差构成纹理描述符，完成特征提取；最后，将特征送入支持向量机(Support Vector Machine，SVM)进行无人机个体识别。

图1 算法流程

2.2 无人机图传信号双谱分析

双谱理论上是三阶累积量的二维傅里叶变换，但在实际信号处理中需要进行谱估计。本文采用简单易于实现的非参数直接谱估计法估计无人机图传信号双谱。若有无人机图传信号为x(t)，下面给出双谱估计步骤。

(1)分段处理

将接收到的无人机图传信号划分为k段长度为M的序列，并对每段信号进行去均值处理，记第j段为xj(n),j=1,2,3,…,k；n=0,2,3,…,M-1。

(2)频谱计算

(1)

式中：j=1,2,…,k；ω=0,1,…,M-1。

(3)频域平滑

对M点序列X(j)(ω)进行频域再取样，使M点序列变为2L1+1个N0点的子序列，即M=(2L1+1)N0。将2L1+1个N0点的子序列按式(2)进行频域平滑处理:

X(j)(ω2+k2)X(j)*(ω1+ω2+k1+k2)。

(2)

(4)时域平滑

将各段信号的双谱进行统计平均，得到无人机图传信号的双谱估计：

(3)

2.3 双谱特征提取

经非参数直接谱估计法得到的无人机图传信号双谱隐含无人机信号的指纹特征。现采用二维双树复小波对双谱进行分解，实现双谱二次特征提取。

定义双树复尺度函数和复小波：

(4)

式中：φh(t)、φg(t)是正交或双正交的尺度函数，h0(n)、g0(n)是相应的低通滤波器，ψh(t)和ψg(t)是正交或双正交的实小波，h1(n)、g1(n)是相应的高通滤波器。二维双树复小波由一维双树复尺度函数和复小波构造，规范化后的二维双树复小波为

(5a)

(5b)

(5c)

(5d)

(5e)

(5f)

上述6个二维双树复小波分别为-75°、-45°、-15°、15°、45°、75°的方向小波，将其展开可得

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

(7a)

(7b)

(7c)

(7d)

(7e)

(7f)

由式(3)、式(6a)～式(7f)可知，无人机图传信号双谱的二维双树复小波变换为

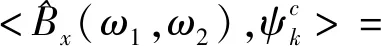
(8)

无人机图传信号双谱6个方向的分解可由分析滤波器组实现，如图2和图3所示。首先，用滤波器{h0(n),h1(n)}和{g0(n),g1(n)}对双谱进行二维可分离小波变换，得到一对低频子带(LL)和3对高频子带(HL、LH、HH)，再将每对高频子带进行加减运算，构成6个方向小波变换系数的实部和虚部。

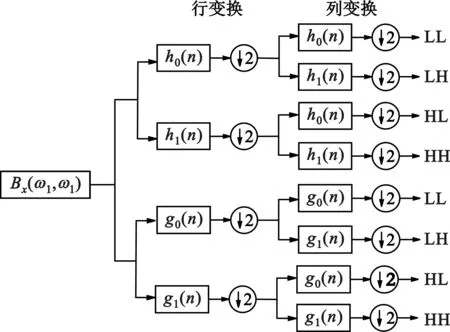
图2 2D_DTCWT实部分析滤波器组

图3 2D_DTCWT虚部分析滤波器组

由上述分析可知，对无人机图传信号双谱进行一次双树复小波分解可得到6个方向子带，记为Pl,n(i,j)，表示分解层数为l、方向为n(n=1,2,…,6)的小波系数图像，对每个子带图像Pl,n(i,j)的幅值|Pl,n(i,j)|分别求取其能量El,n和能量偏差Rl,n：

(9)

(10)

式(9)和式(10)中，M×N是子带图像Pl,n(i,j)的大小。假设对图像进行L层分解，则图像的纹理描述符可表示为

fl,n=(E1,1…,EL,6,R1,1…RL,6)。

(11)

式(11)中，无人机图传信号双谱分解后的子带图能量和能量偏差构成L×12维特征。

3 实验与分析

3.1 不同型号无人机个体识别实验

暗室采集DJI Phantom 3 Advanced(下文称UAV1)和 Mavic Pro(下文称UAV2)无人机图传信号，双谱估计结果如图4所示。

图4 无人机图传信号双谱估计结果

由图4可以看出，不同型号无人机图传信号的双谱图像有明显差异，个体特征明显，故提取信号双谱特征作为分类依据是可行的。

将本文算法与直接用双谱矩阵在特征提取用时、模型训练用时、准确率三个维度进行对比。实验环境为Matlab2017软件，不同型号无人机图传信号各取500个样本，实验均采用10次10折交叉验证法，双谱预设二维双树复小波分解层数为2层，构成24维特征。2D_DTCWT与直接用双谱分类对比结果如表1所示。本文算法对1 000个样本进行二次特征提取用时7.386 s，支持向量机模型训练时间0.651 s，共8.037 s，是直接用双谱矩阵进行分类的1/22，运算效率得到大幅提升。此外，本文算法准确率也有一定程度的提升。

表1 2D_DTCWT与直接双谱对比结果

为检验本文算法与其他二次特征提取算法的性能优劣，将其与文献[5]的基于矩形积分双谱和文献[9]的基于灰度共生矩阵进行对比，结果如表2所示。本文算法用时为8.037 s，准确率为94.9%。相较于矩形积分双谱算法，本文算法总计用时高5.215 s，但准确率提升了3.7%。基于灰度共生矩阵算法准确率为93.1%，算法总用时897.015 s，相较之下本文算法用时约是其1/112，而准确率提升了1.8%

表2 不同二次特征提取算法的性能对比

3.2 同型号无人机个体识别实验

由于实验条件有限，无法采集到三个同型号无人机信号，现将采集DJI Phantom 3 Advanced图传信号依据泰勒模型模拟出三个具有细微差异的信号源代表同型号无人机。取阶数N为5，泰勒级数分别是a1=[1 0.5 0.3 0.05 0.2]、a2=[1 0.08 0.6 0.4 0.8]、a3=[1 0.0 0.01 0.3 0.15][13]。经泰勒级数模型构造的信号源sig-1、sig-2、sig-3双谱等高线图如图5所示，可以发现三个信号双谱等高线具有相似的分布特征，但也存在细微差异。

图5 不同信号源不同时刻双谱等高线图

现利用2D_DTCWT分别对三个信号双谱进行1层分解，原双谱为128×128矩阵，经分解后变为如图6～8所示的6个64×64的方向子带图，依次是-75°、-45°、-15°、15°、45°、75°。可以看出，不同信号双谱分解后的各方向子带图像有明显差异，个体特征明显。

图6 sig_1双谱分解后各方向子带图像

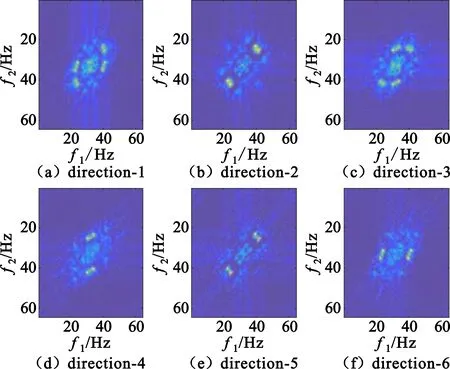
图8 sig-3双谱分解后各方向子带图像

为研究不同分解层数对识别准确率的影响，现预设分解层数为4，即无人机图传信号双谱分解后的子带图像能量和能量偏差构成48维特征，其中1～24维特征为子带图像能量，25～48维特征为子带图像能量偏差，将其可视化后如图9所示，其中蓝色为sig-1特征，橙色为sig-2特征，黄色为sig-3特征。

图9 三个信号源多维特征可视化

从图9中可以看出，分解1层后的子带图像能量1～6维和能量偏差25～32维特征线条相对混乱，不同信号源交叉部分较多。相比较而言，分解2～4层后的数据线条整齐，不同信号源之间重叠部分较少。现分别选取不同分解层数的特征进行分类识别，结果如表3所示，可见分解后第二层的6个方向子带图像纹理特征用于分类准确率最高，为89.1%，故后文采用此特征。

表3 不同特征的识别准确率分析

为验证本文算法较之基于积分双谱的方法、基于灰度共生矩阵的方法和小波变换法[14]对无人机图传信号分类识别的性能提升，将经泰勒级数模型构造的三个信号源分别加上相同信噪比的高斯白噪声，在信噪比0～30 dB范围内的识别准确率如图10所示。从图中看出，在0～30 dB信噪比范围内本文算法的识别准确率更优。在20～30 dB信噪比范围内，基于积分双谱的方法和基于灰度共生矩阵的方法识别准确率较低，最高为80.7%，相比之下基于本文算法提取的双谱特征分类效果更佳，识别准确率最高能达到86.1%。本文算法与基于小波分析法相比，在高信噪比下性能优势不是特别明显，但在信噪比0～20 dB时，本文算法识别准确率下降速度相对较缓慢。这表明与基于小波分析法相比，本文算法受噪声影响更小，在信噪比变化时稳定性更高，性能更优，更能适应实际应用场景。

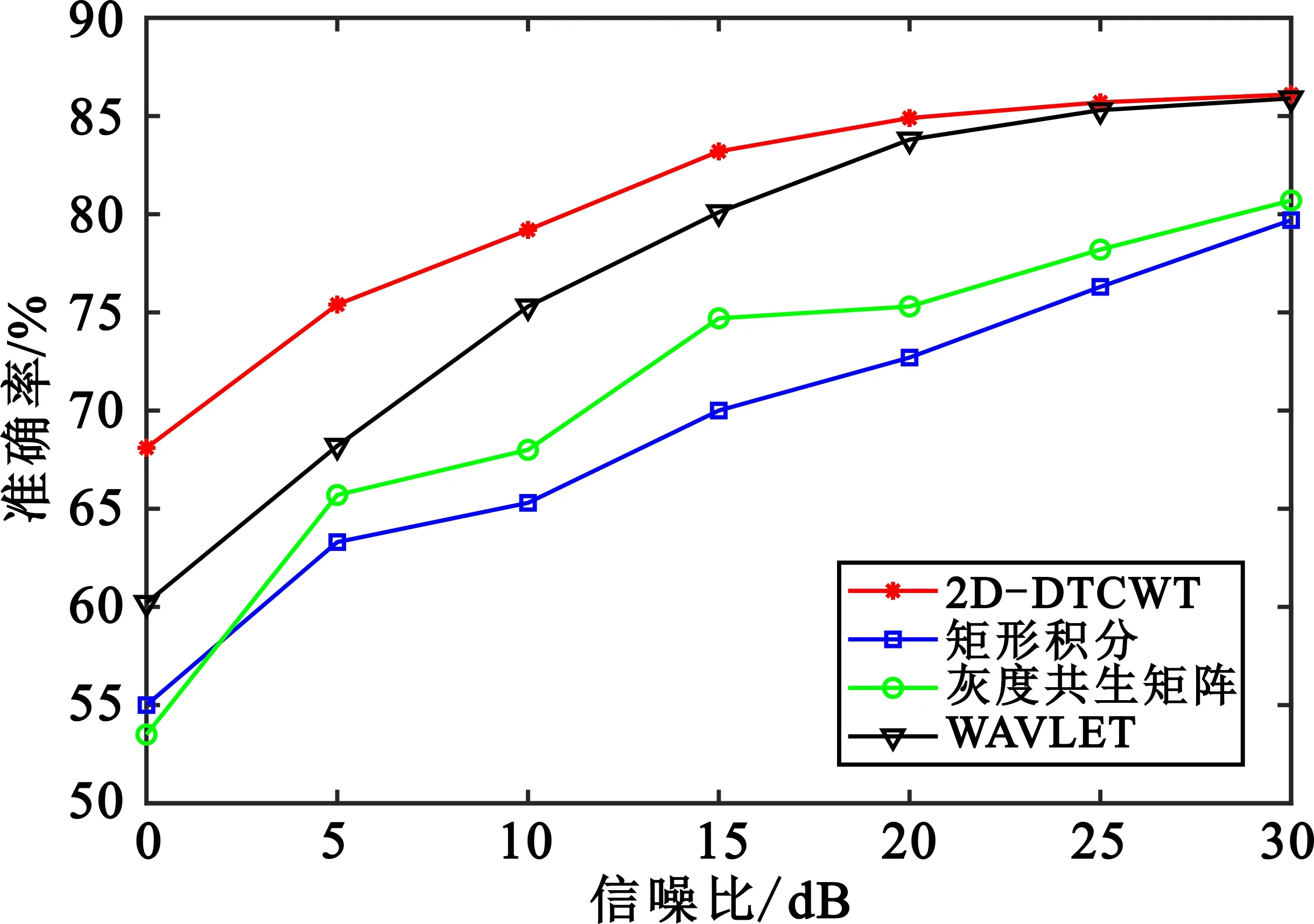
图10 不同信噪比下的识别准确率分析

4 结束语

在无人机个体识别问题中，针对双谱矩阵维度高、运算效率低的问题，本文采用二维双树复小波变换对双谱进行二次特征提取。该方法在不损失双谱值的情况下，利用滤波器组对双谱进行6个方向的滤波，将大小为128×128的双谱值转换为24维的图像纹理特征。在Phantom 3 Advanced与Mavic Pro个体识别实验中，本文算法比直接用双谱矩阵进行分类的运算效率高21倍，准确率相较于基于积分双谱、基于灰度共生矩阵更高，可达94.9%，满足准确性和实时性的需求。在识别通过泰勒模型构造的具有细微差异的无人机信号时，当信噪比大于5 dB时，识别准确率大于75.4%。此外，与小波分析法相比，在低信噪比环境中本文算法识别准确率下降速度相对较缓慢，稳定性更高。

下一步工作将进行外场测试，验证无人机飞行状态对算法的影响。