基于基流和降水的水文气象综合干旱指数构建及在渭河的应用

樊晶晶，孙 雪，周 斌*，刘登峰，刘 纯，林 帅，黎云云

(1.河北工程大学水利水电学院，河北 邯郸 056107；2.西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048；3.绵阳师范学院资源环境工程学院，四川 绵阳 621000)

在全球气温升高和水资源过度利用的趋势下，水资源短缺是中国普遍存在的问题，尤其在受干旱影响严重的地区，保障河流中能够维持一定的流量显得日益重要，即保证生态基流长期存在[1]。生态基流是指为维持河流基本形态和基本生态功能的河道内最小流量[2]，对于干旱地区的生物生长、生态平衡和流域健康有着至关重要的作用[3]。因此，以基流为因子，对受干旱影响严重地区进行干旱的风险评估和监测依旧是必要的研究。

关于基流干旱的研究较少，其中李苗等[4]对白洋淀区域的日径流进行基流分割，得出基流干旱对极端气象干旱的响应长于径流干旱的结论；周洋等[5]计算了极端干旱条件下渭河宝鸡段的生态基流量，并表明生态基流量在极端干旱情况下对于季节性河流有重要意义。对于干旱的研究，国内外诸多学者建立了许多单一的干旱指数来判断干旱的严重程度，但是影响干旱的因素极为复杂，想对干旱做出更准确的预判，就需要建立结合多种干旱影响因素的干旱指数，对干旱做出综合判断。近几年，诸多学者通过不同的方法建立了多种综合气象、水文、农业等的干旱指数[6-8]，其中在气象水文综合指数的构建上，张迎等[9]以径流和降水为指标，建立了新的气象水文干旱指数MSDIP(Multivariate Standardized Drought Index,parametrically)，并对渭河的干旱情况进行了判断；粟晓玲等[10]基于Gumbel Copula函数，发展了联合SPEI[11](Standardized Precipitation Evapotranspiration Index)和SDI[12](Streamflow Drought Index) 的气象水文综合干旱指数MHDI (Multivariate Standardized Drought Index);朱悦璐等[13]利用VIC模型，结合降水和径流数据，在GPP (Gringorten Plotting Position)算法的基础上建立了NMSDI (Non-parametric Multivariate Standardized Drought Index)指数，并对黄河进行了实例分析。以上综合气象水文干旱指数均是在径流基础上完成，而基流是径流很重要的组成部分，也是重要的水文特征之一，在干旱的气候下，降水对径流的补给基本终止，通过地下水补给的基流就成为枯水季径流的主要来源，故本文采用基流作为构建干旱指数的变量之一。近几十年来，干旱成为渭河流域最严重的灾害之一，其给所在地居民、农业、工业等都带来了很大影响，对干旱进行更加准确的评估是各部门迫在眉睫的任务，而建立更加合适、准确的干旱指数是对干旱情况进行分析的基础，本文所建立的综合干旱指数旨在为渭河流域干旱的判断起到积极的作用，并力图帮助政府部门对干旱事件的发生做出准确的评估。

1 研究资料及方法

1.1 研究区域

渭河是黄河的第一大支流，发源于甘肃省内，流经甘肃、宁夏、陕西三省，在陕西省潼关县汇入黄河。渭河流域(103.5～110.5°E,33.5～37.5°N)属于温带大陆性季风气候，汛期集中在夏季，年平均气温为7.8～13.5℃，年降水量约为500～800 mm。

渭河林家村站以上为上游，林家村至咸阳为中游，咸阳至入黄口为下游。以渭河流域下游重要干流测站华县站(109°46′E,34°35′N)为研究对象，其控制流域面积为106 498 km2，占渭河干流总面积的79%，华县站位于陕西省关中平原，该区域受人类活动影响大，是干旱影响严重的地区之一(图1)。

1.2 数据来源

采用的降水数据为中国气象数据网(http://data.cma.cn)提供的渭河流域内延安、华山、镇安等20个国家气象站(表1)1960—2010年的月降水量数据，采用均值法计算得面降水量；径流数据采用中华人民共和国水文年鉴(黄河流域水文资料)中渭河华县水文站1960—2010年的实测日径流量，经公式计算得到的月径流深；基流数据在日径流量的基础上，利用数字滤波法分割出基流，经公式计算得到月基流深。

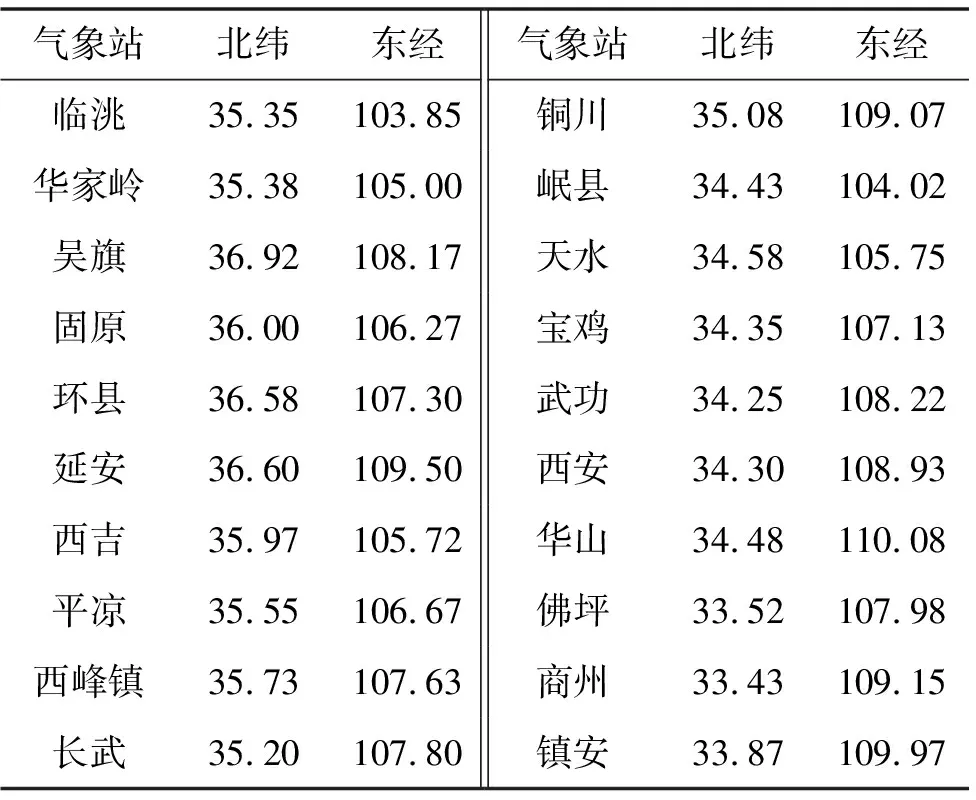
表1 渭河流域20个国家气象站 单位：(°)

1.3 研究方法

选取渭河华县站的降水(气象)和径流(水文)数据，首先利用数字滤波法分割出所需的基流数据，后通过拟合优度检验选择合适的边缘分布函数和Copula函数，得到气象和水文要素联合分布概率，后借鉴SPI[14](Standardized Precipitation Index)干旱评价模式，对该联合分布概率进行标准化处理得到新的综合干旱指数CPBI，并确定其干旱等级划分规则，在以上基础上，结合Mann-Kendall秩次检验法、有序聚类法、里海哈林法以及游程理论分析了渭河的干旱情况。

1.3.1数字滤波法(F3)

数字滤波法是NATHAN等[15]于1990年首次提出的基流分割方法，其原理是将径流视为高频信号、基流视为低频信号，通过数字滤波器将高频信号和低频信号分离，从而把基流从日径流量中分割出来。采用数字滤波法中的F3法分割渭河流域华县站的基流，该方法是CHAPMAN于1991年对由NATHAN等[15]于1999年提出的F1法进行的改进，其计算公式为：

(1)

式中f1——退水系数，取0.95；Qt——t时刻的地表径流；Qb(t-1)——t-1时刻的地表径流；Qbt——最后分离出来的基流量。

1.3.2Copula函数

Copula是定义域为[0,1]的均匀分布的多维联合分布函数，它可以将多个随机变量的边缘分布连接起来得到其联合分布[17]。

Sklar定理[18]：令H为一个n维分布函数，其边缘分布为F1,F2,…,Fn，则存在一个n-Copula函数C，使得对任意x∈Rn有：

H(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]

(2)

如果F1,F2,…,Fn是连续的，则C是唯一的，相反地，如果C是一个n-Copula，F1,F2,…,Fn为分布函数，则上式中所定义的函数H是一个n维分布函数，其边缘分布为F1,F2,…,Fn[18]。

利用Copula进行两变量联合分布，首先确定各变量的边缘分布，其次确定Copula函数的参数，根据评价指标选取Copula函数，建立联合分布，最后根据所建分布进行相应的统计分析。

拟合优度检验时采用均方根误差准则(RMSE,Root Mean Square Error Criterion)、赤池信息量准则(AIC,Akaike Information Criterion)和贝叶斯信息准则(BIC,Bayesian Information Criterion)，选取数值最小的Copula函数作为应用函数，计算见式(3)—(6)[19]：

(3)

(4)

AIC=nln(MSE)+2l

(5)

BIC=nln(MSE)+l′ln(n)

(6)

式中l——与Copula函数的参数个数一致；Pei、Pi——联合分布的经验频率与理论频率；n——序列的长度[19]。

2 综合干旱指数CPBI的构建

利用皮尔逊相关系数判断渭河流域降雨和基流之间的相关性，发现相对应月数据间的相关性系数为0.49，存在弱相关性，年数据间的相关性系数为0.86，也存在强相关性，2组数据序列均通过0.05的置信区间检验且均呈正相关关系，故可利用Copula函数进行联合分布函数的构建。

应用渭河流域华县站1960—2010年的月降水、基流数据，首先采用极大似然法进行2种变量的参数估计，得到各变量的最佳边缘分布，并采用3种Copula函数进行两变量联合分布的拟合，通过拟合优度检验得到拟合效果最好的联合分布函数[20]。

2.1 最佳边缘分布函数的确定

利用极大似然法得到降水、基流的参数(表2)。

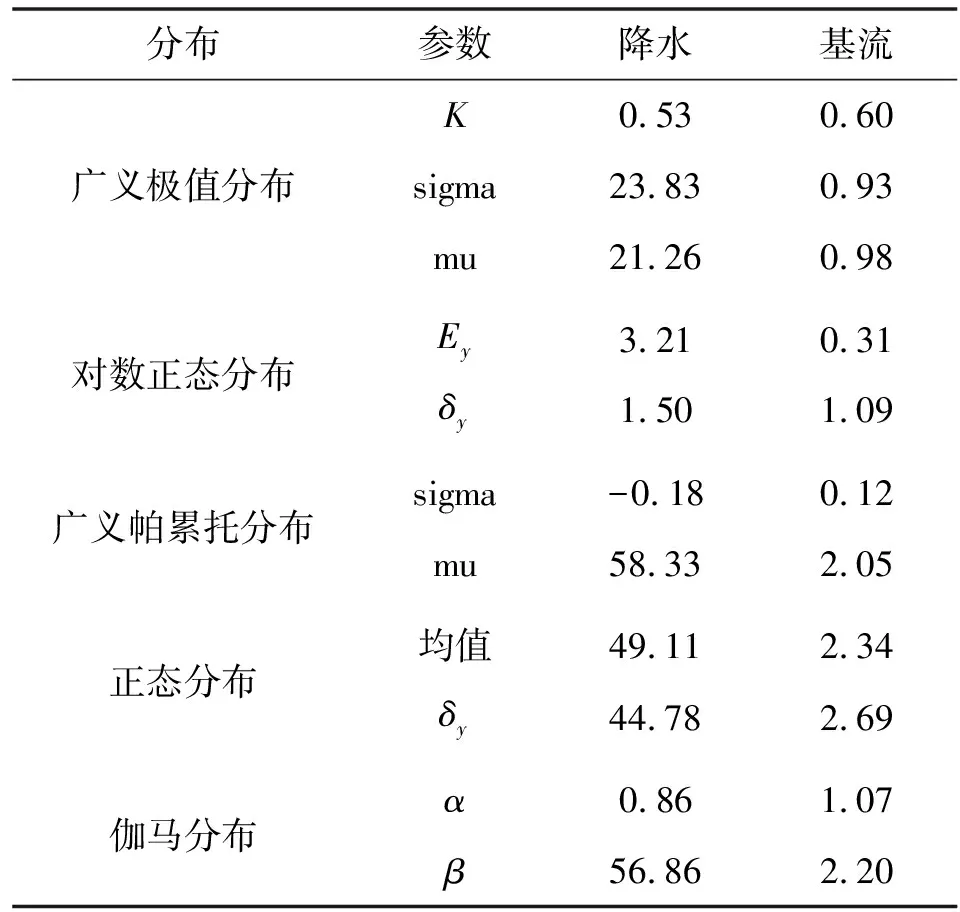
表2 渭河华县站降水、基流分布参数估计

采用AIC赤池信息量准则和RMSE均方根误差准则进行边缘分布拟合优度检验[21]，检验结果见表3。

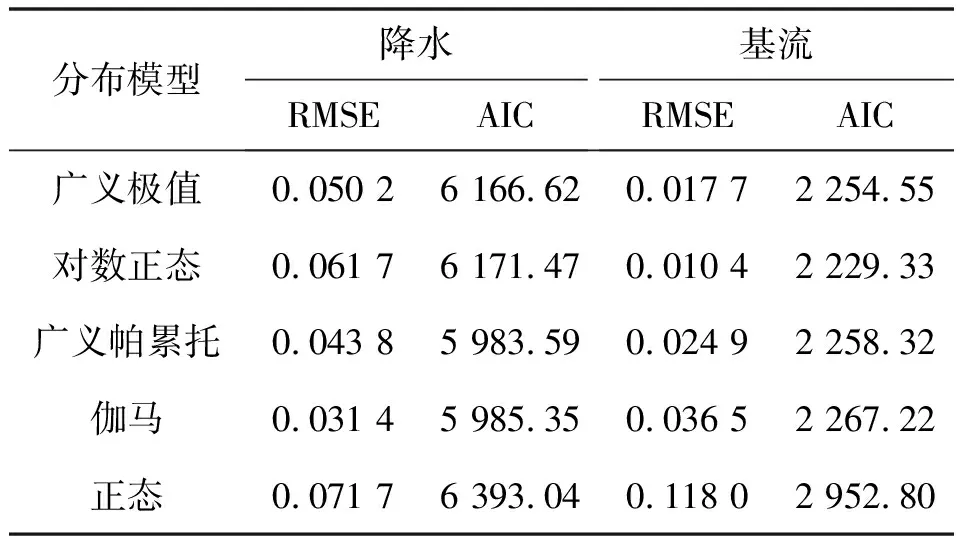
表3 降水、基流边缘分布模型拟合优度检验结果

RMSE与AIC最小时对应的降水和基流的边缘分布函数为广义帕累托分布和对数正态分布。

2.2 Copula函数的确定

采用AIC赤池信息量准则和BIC贝叶斯信息准则对Copula函数进行拟合优度检验，选择最优的Copula函数[20]，结果见表4。

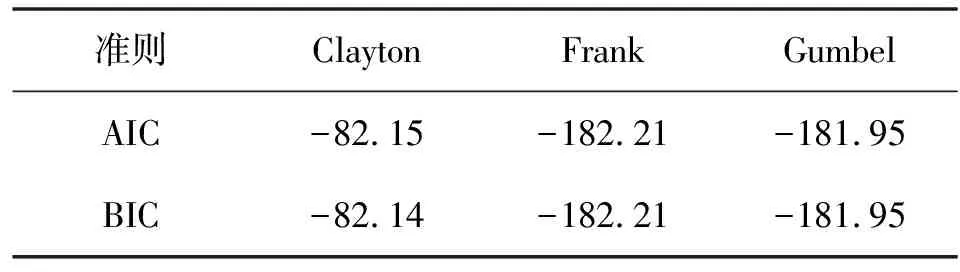
表4 Copula函数的拟合优度检验

根据信息最小准则，可看出降水-基流联合分布采用Frank Copula函数。

2.3 综合干旱指数CPBI的建立

以面降水量Q和基流深B为随机变量，q和b为降水、基流的某一数值，假设F(q)和G(b)为两随机变量的边缘分布，则它们的联合分布H可以表达为：

H(q≤Q,b≤B)=C(F(q),G(b))=p

(7)

则CPBI的表达式为：

CPBI=φ-1(p)

(8)

式中φ——标准正态分布函数；p——累计联合概率。

CPBI综合降水(气象)和基流(水文)2种要素得到，能够同时反映气象和水文干旱的特征，参照前人的研究(表5)，以干旱的严重程度为根据，以-0.5为干旱阈值，根据SPI的干旱等级划分方法确定的CPBI干旱等级(表6)。

表5 参考文献干旱等级划分

表6 CPBI干旱等级划分

3 结果及分析

计算月尺度的SPI、SRI和CPBI，通过对比来验证CPBI的优越性，并分析了渭河的气象水文综合干旱特征。

3.1 CPBI的适用性

图2是渭河华县站月尺度下3个指数的变化情况(图中标注出干旱发生的阈值线)，从图中可以看出SPI的波动起伏较大，而SRI较为平稳，CPBI的变化曲线与SPI和SRI的相似度较高，有较好的一致性。CPBI与SPI、SRI的皮尔逊相关系数分别为0.673 0、0.759 4，均在0.65以上，有较强的相关性。这说明CPBI具有一定的有效性。

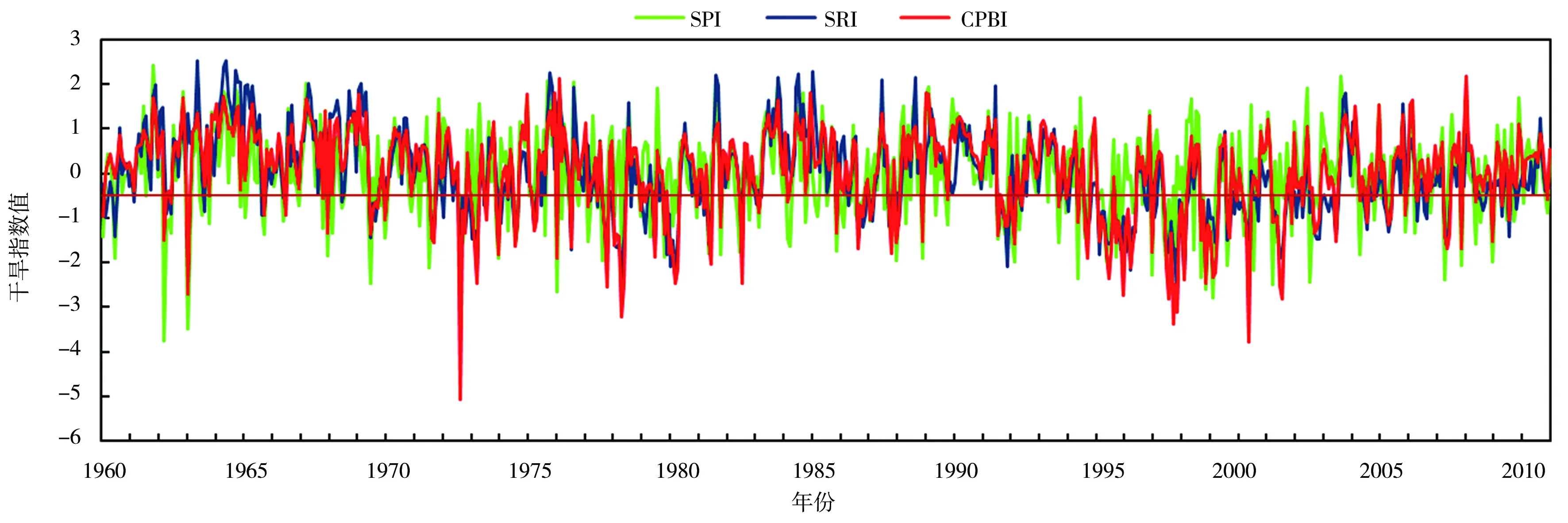
a)1960—2010年干旱指数值

b)1994—2002年干旱指数值

将1994—2001年指数变化曲线放大，可以更加直观地看出3种曲线的异同处。CPBI的变化规律、走向趋势与SPI和SRI大致相同，图2b中显示，在1996、1997年下旬和2001年中旬SPI指数大于阈值，但SRI指数小于阈值，说明在这2个时间段发生了水文干旱没有发生气象干旱，而CPBI却很好地识别了干旱的发生，同时可以发现SPI比SRI更早地预判到干旱发生，SRI比SPI更晚地预判到干旱的结束，而CPBI可以在SRI之前捕捉到干旱的发生，在SPI之后捕捉到干旱的结束。CPBI综合了SPI和SRI指数的特点，既能像降水决定的SPI指数一样捕捉到气象因素对干旱的影响，又能像受径流决定的SRI指数一样将水文要素识别出来。以上均说明CPBI具有SPI和SRI的优点，并可以有效地捕捉到干旱的发生，具有一定的优越性。

3种干旱指数变化曲线显示(图3)，在20世纪70、90年代和21世纪00年代干旱发生较频繁且干旱情况严重。资料[23]显示1979年10月至1980年5月连旱200天，降水偏少6～8成，陕西省春旱21 000万hm2；90年代的严重干旱则主要发生在后期，即1997—1998年，中国气象大典(陕西卷)[24]记载渭河流域发生的干旱情况：1997年华县站首次发生了汛期连续3天断流，1998年渭河流量接近历史同期最枯流量，多条中小河道干涸断流，充分证明渭河流域在1997—1998年水文干旱的严重情况；到21世纪，干旱指数发生明显变化，00年代的严重干旱主要发生在2000、2001年，2002—2010年干旱指数相较于之前明显增大[25]。

a)春季

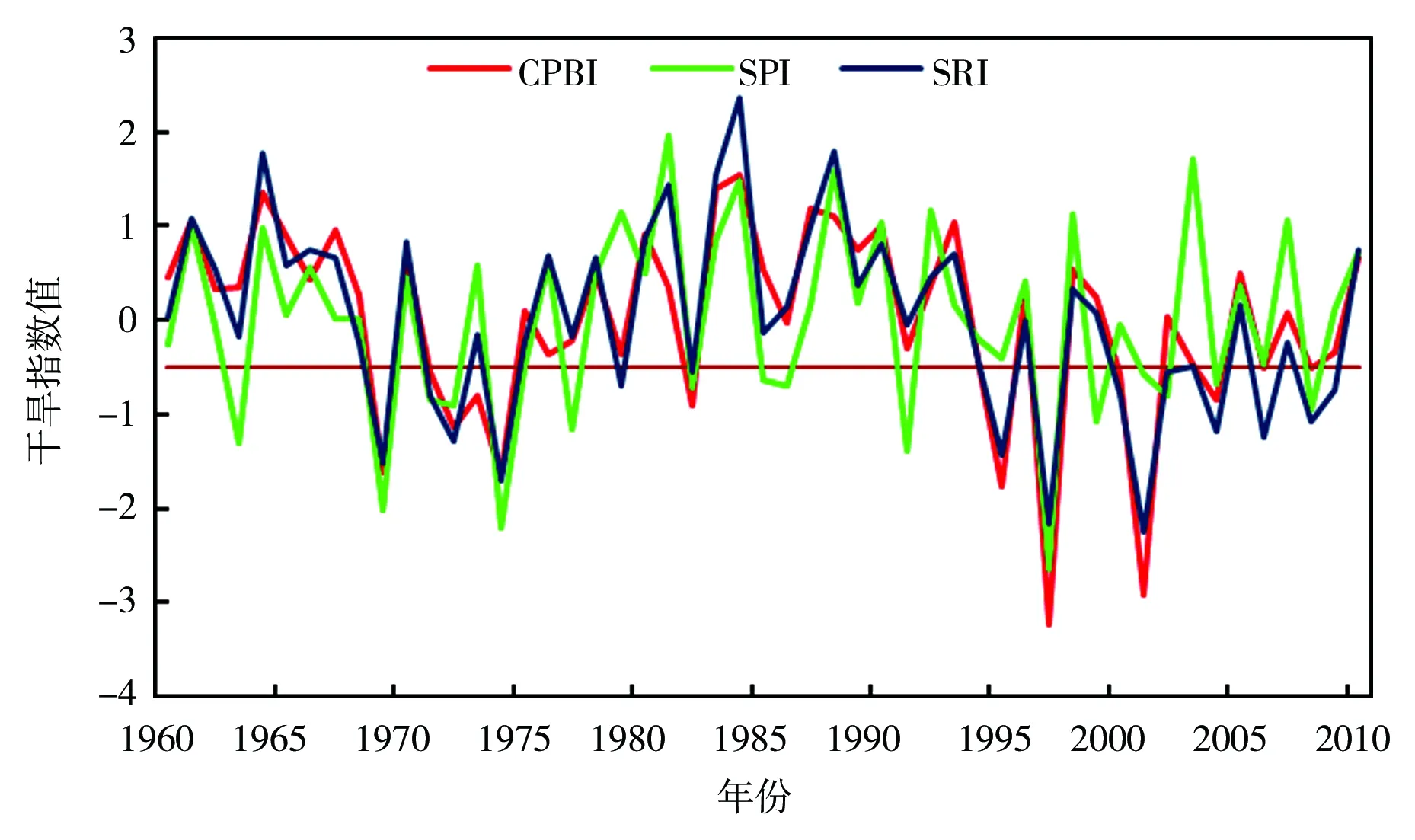
b)夏季

c)秋季

在干旱指数的基础上，利用游程理论，分析出渭河华县站1960—2010年的干旱特征值，具体统计量见表7。

其中，干旱次数代表干旱发生的频次，平均历时和平均强度表示干旱的严重程度，而最大历时和最大强度表示极端干旱的严重程度。从统计数据来看，CPBI序列的干旱次数比SPI少但比SRI多，这说明其综合了气象和水文的特点，但其最大强度、平均强度、总历时和总强度都最大，表明CPBI将干旱情况描述得比较严重，对干旱发生有较好的警示作用。

综上所述，经过Frank Copula函数联合所得到的综合干旱指数CPBI具有一定的有效性、优越性和准确性，CPBI指数对于渭河干旱情况的预判可以提供一定的理论支持。

3.2 渭河的干旱特性

3.2.1CPBI的年及四季变化情况

图3为渭河华县站1960—2010年年度和季度的干旱指数变化情况，可以看出，春季干旱主要发生在1978、1996、2000年前后，而1978年春季降水比较充分，故发生的干旱主要为水文干旱，也可能原因与气温有关，1996、2000年气象和水文均发生较严重干旱；夏季干旱发生在1969、1974、1997、2001年前后，其中2001年未发生气象干旱；秋季干旱发生在1995、1997、2002年前后，1997年干旱最为严重；冬季较为严重的发生在1979、1997年前后，但可能由于基流补充径流的原因，水文情况没有明显起伏且未发生严重干旱，主要干旱原因由降水造成。综合以上并结合图3e，1960—2010年发生干旱的3个主要时间点为1978、1997、2000年，其中1978年前后发生的较严重干旱只由春季造成，1997年几乎四季都处于严重的干旱情况，2000年前后除冬季外，均发生较严重干旱。

近51年来，渭河华县站各个季节发生干旱的占比均低于50%(表8)，轻旱发生的次数最多。在发生中度以上较为严重的干旱占比中，春季发生中旱的占比最多，为5.88%；夏季发生重度干旱的占比最多，为5.88%；秋季发生重度干旱的占比最多，为7.84%；冬季发生中度干旱和极端干旱的占比同样多，为5.88%。秋季发生中旱以上干旱事件的频率最高，夏季最低，冬季发生极端干旱的频率最高。主要原因是冬季属于极端干旱高发期是由于冬季降水相对其他四季偏少，其次为春秋季，故春秋季发生中旱以上的频率比夏季高。

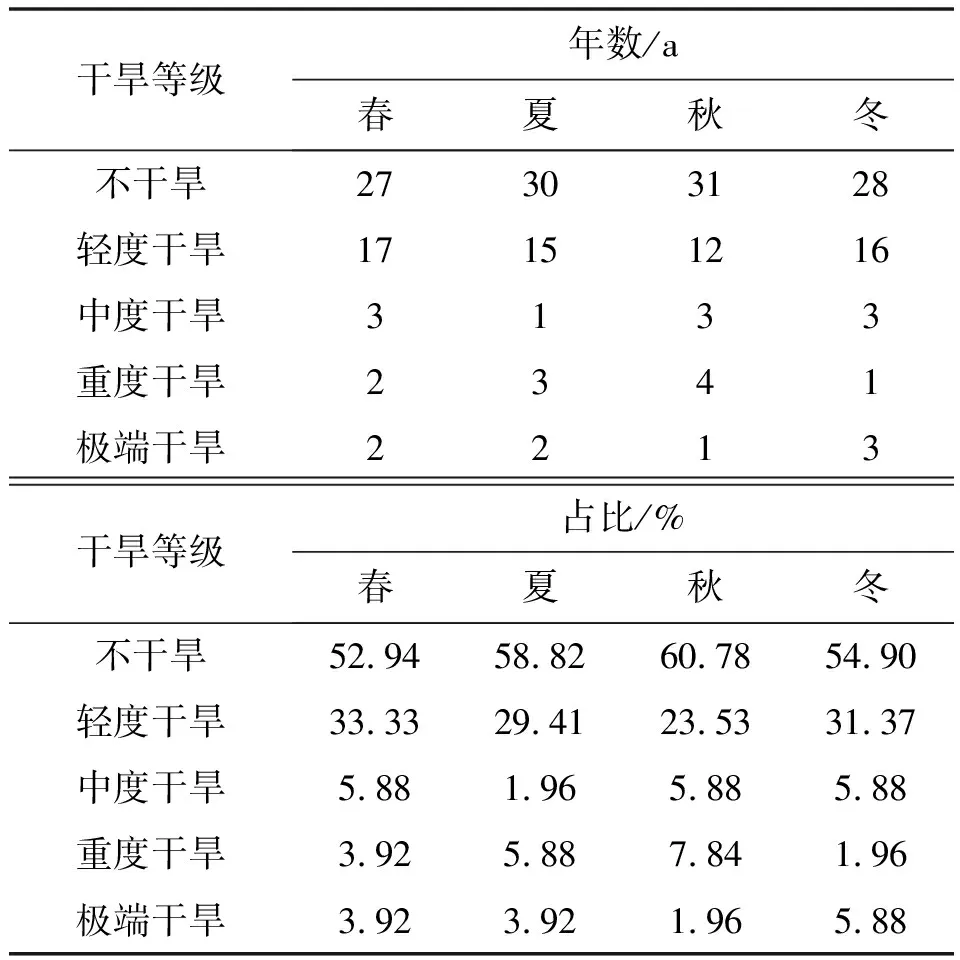
表8 渭河华县站四季发生干旱等级情况

3.2.2CPBI序列趋势及突变点识别

渭河华县站年及季尺度的CPBI序列趋势检验情况(表9)，在显著性水平等于0.05条件下的肯德尔秩次相关检验值，若检验值|U|≥1.96则通过显著性检验，U>0，则呈上升趋势，U<0，则呈下降趋势。

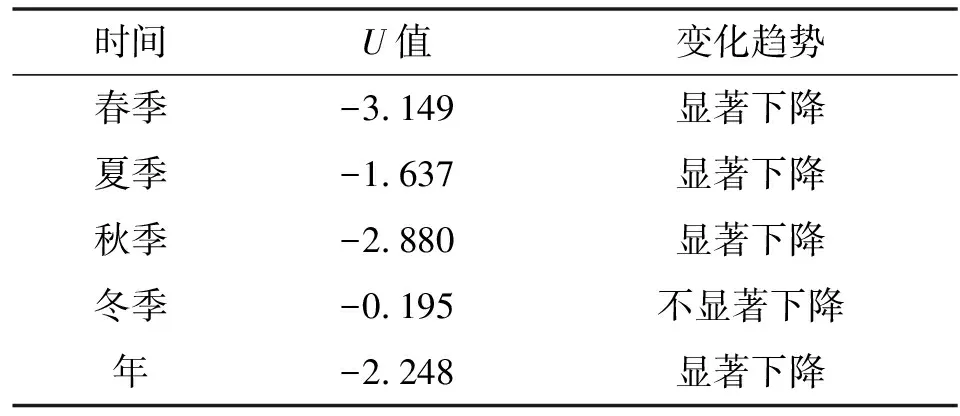
表9 CPBI趋势检验

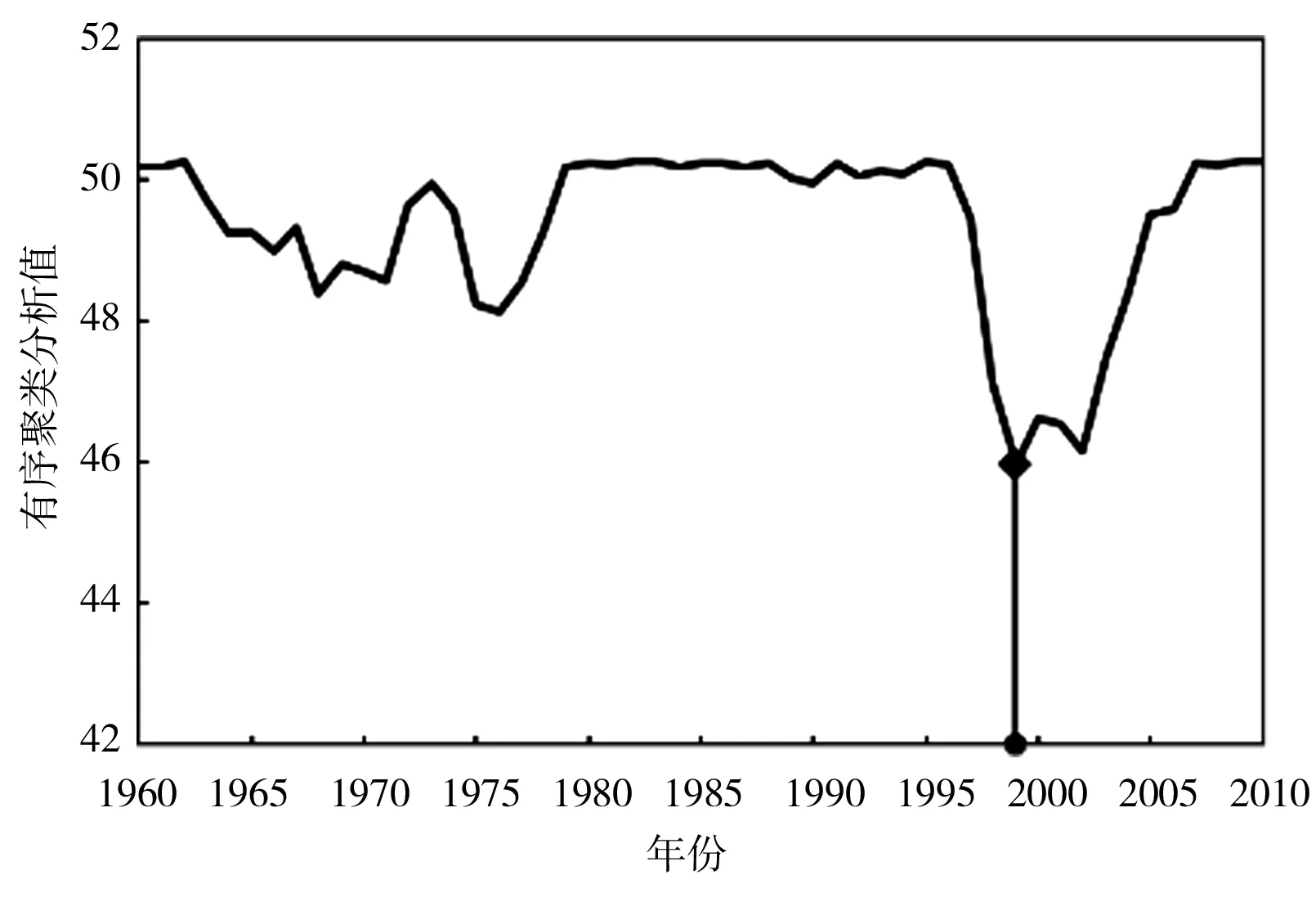
采用肯德尔秩次检验法对渭河流域CPBI序列进行趋势分析，除冬季外，其他3个季节及年尺度均呈显著下降趋势，说明渭河的干旱情况加剧；采用有序聚类法和里海哈林法对CPBI序列进行突变点识别(图4、表10)，经过2种方法的相互验证和比较，渭河流域1960—2010年51年的年突变点发生在1975年，据相关文献显示，渭河降水[26]和径流[27]的突变均发生在1976年前后，作为CPBI的主要影响因素，降水和径流发突变对CPBI发突变具有很大影响；春季突变年份为1994年，该年3月陕西各地降水普遍偏少4～7成，且4—5月降水极少，尤其渭河所属的关中地区降水偏少9成；夏季发生在1993年，该年夏季关中地区降水比常年同期减少1～3成，导致农田播种困难，至7月上旬，全省受灾农田达80万hm2；秋季发生在1985年，1985年7—8月全程降水偏少4～6成，导致受旱秋田140万hm2[24]；冬季2种方法检验出的突变点不同且均不显著，故推断冬季不存在突变年份，这与前人的研究结果相吻合[28]。

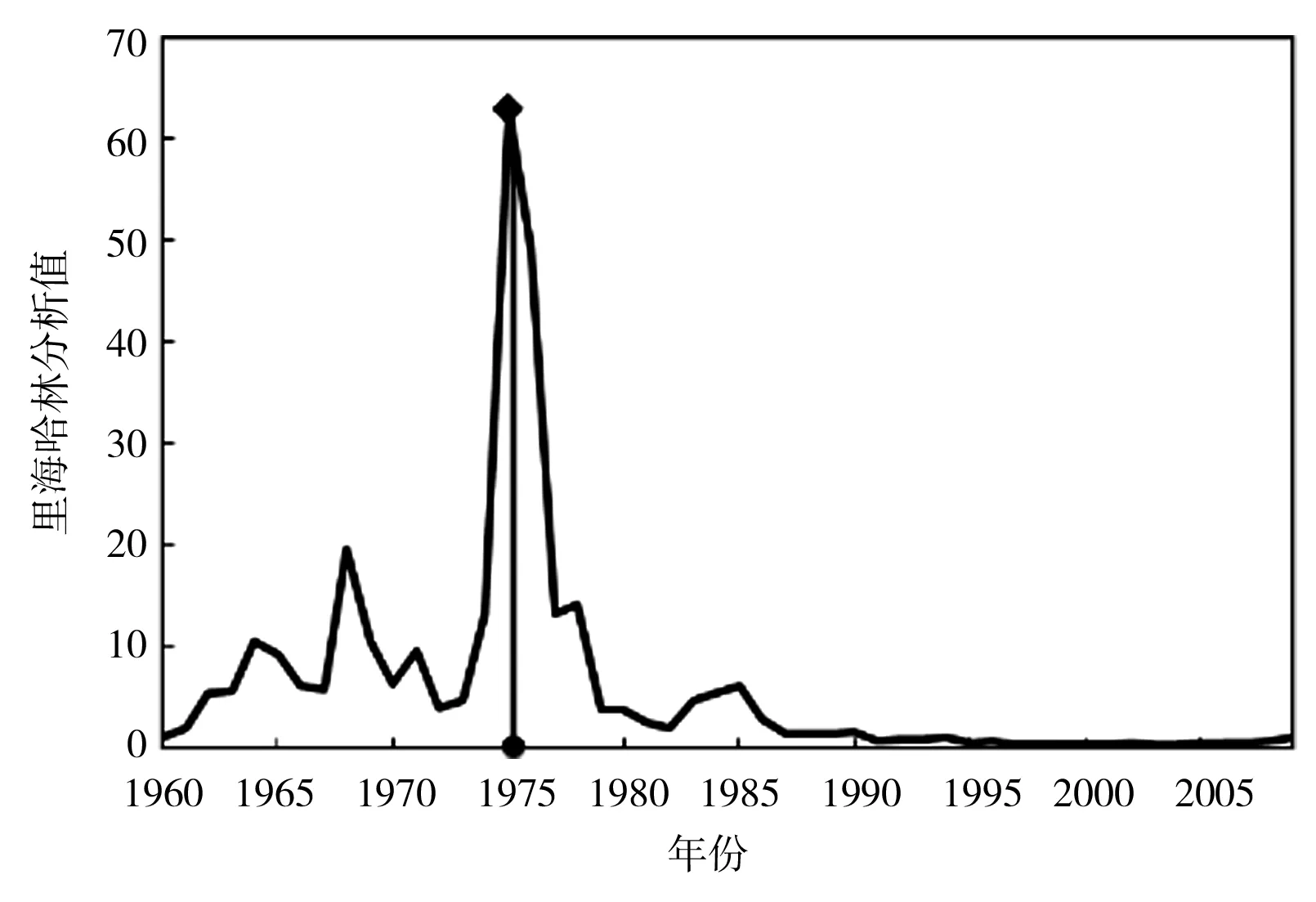
a)全年里海哈林分析值

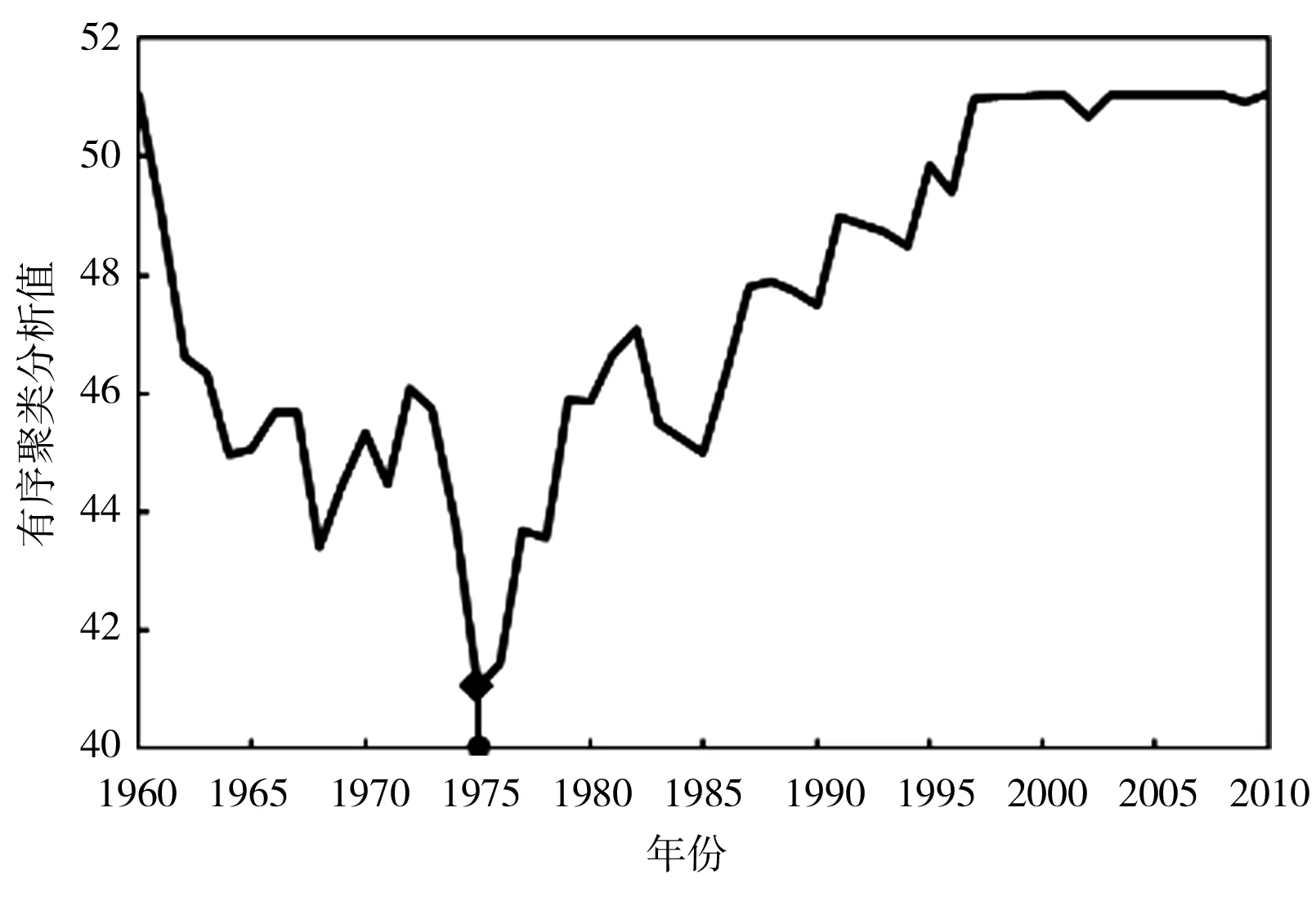
b)全年有序聚类分析值

c)春季里海哈林分析值

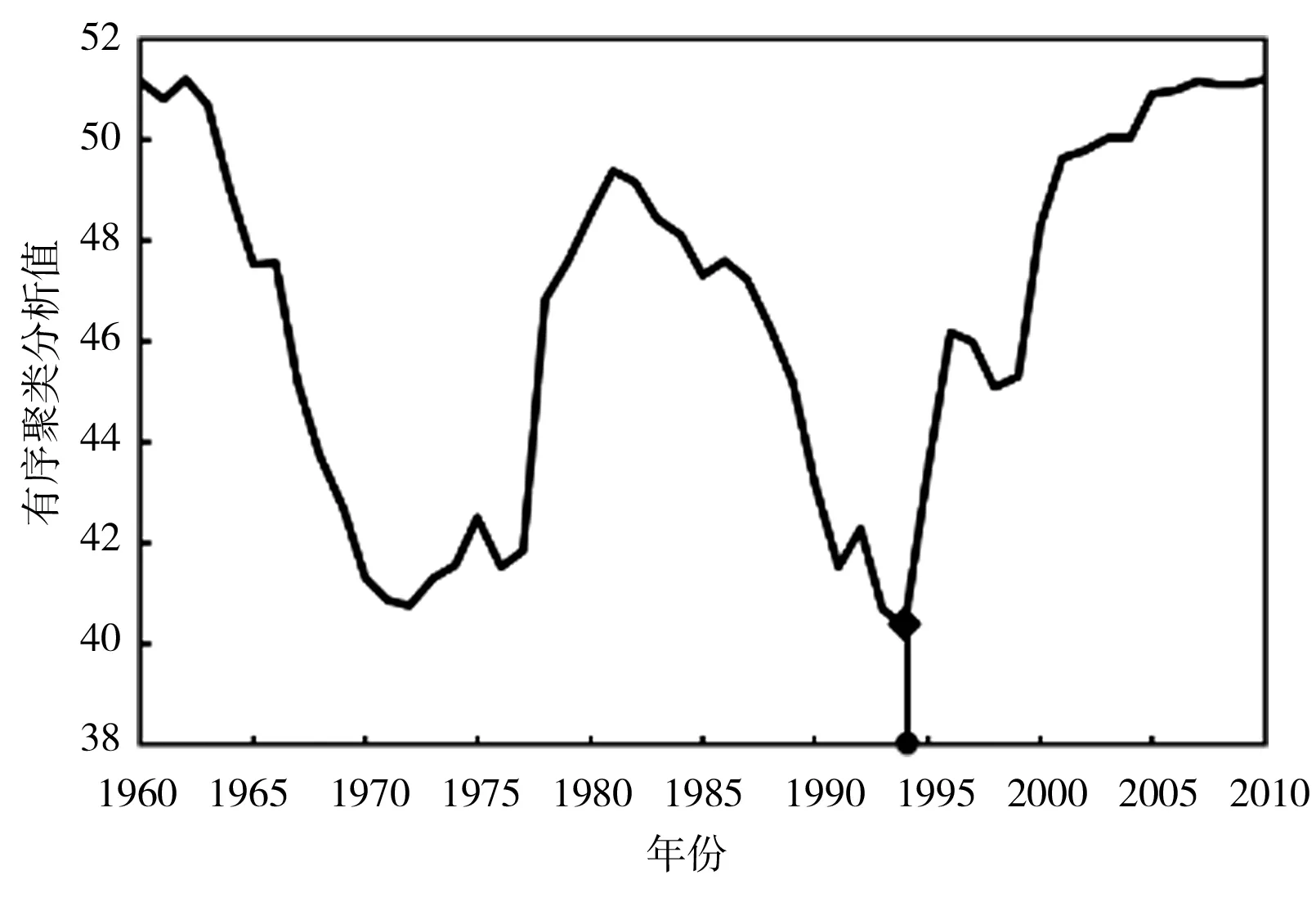
d)春季有序聚类分析值

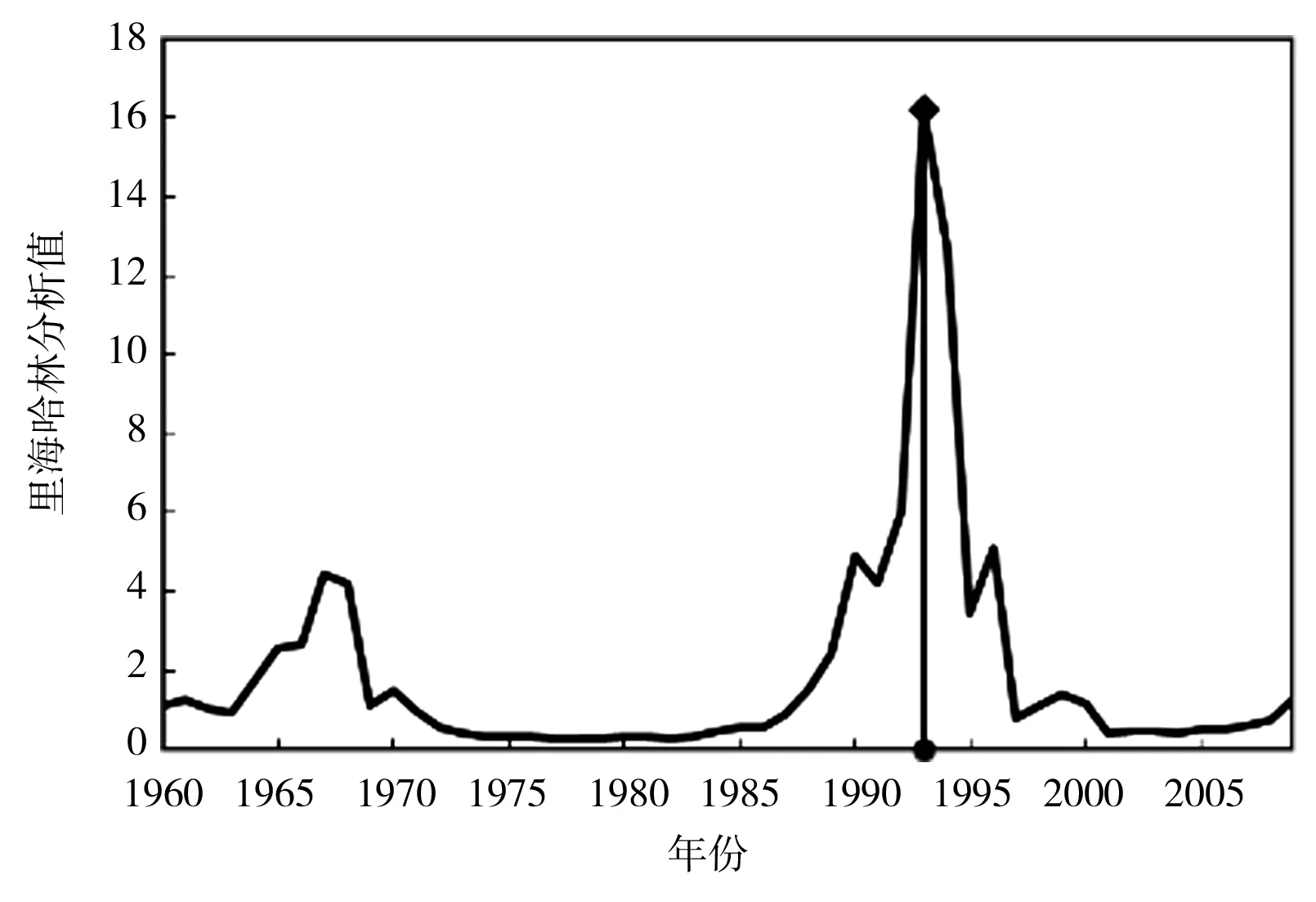
e)夏季里海哈林分析值

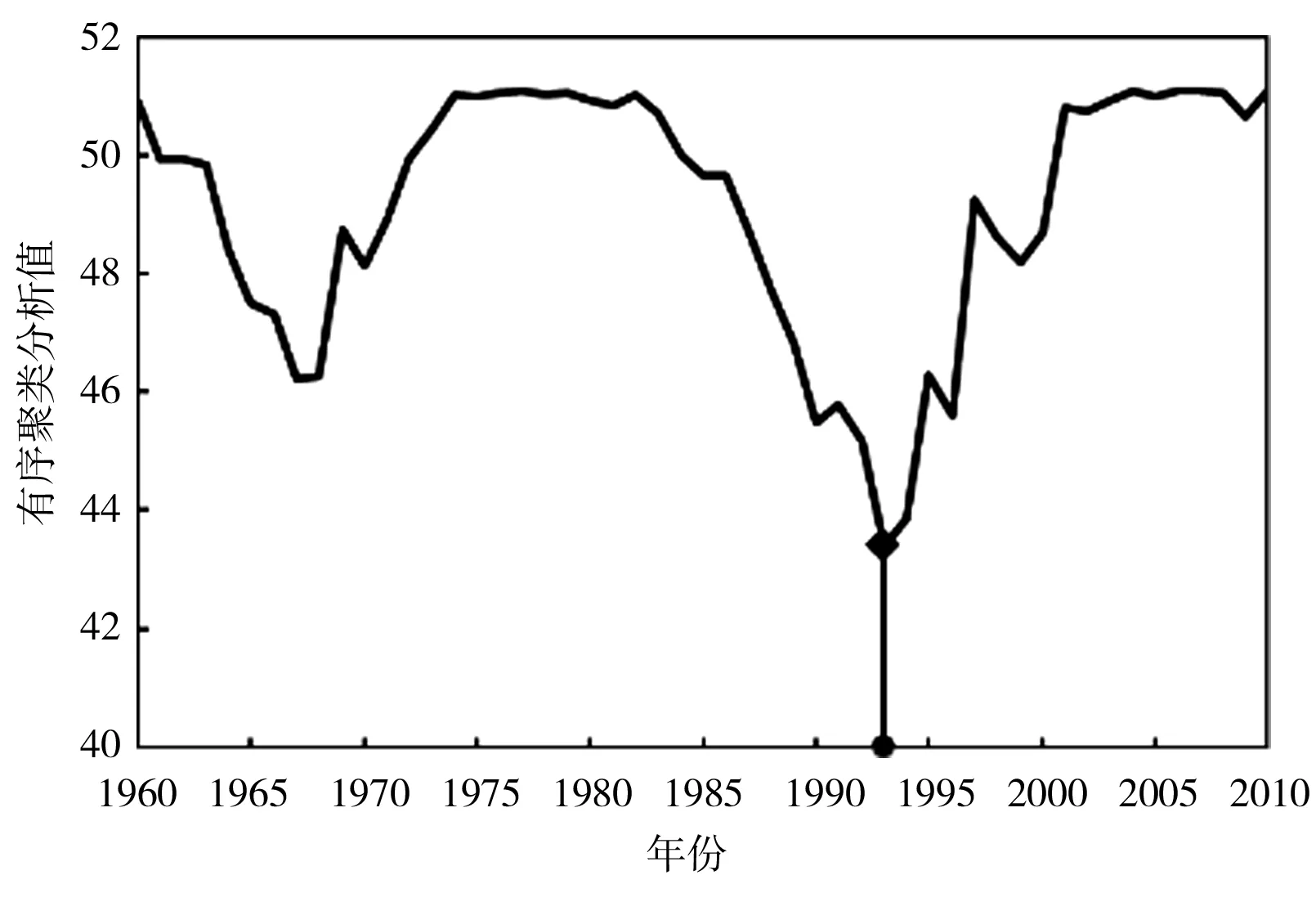
f)夏季有序聚类分析值

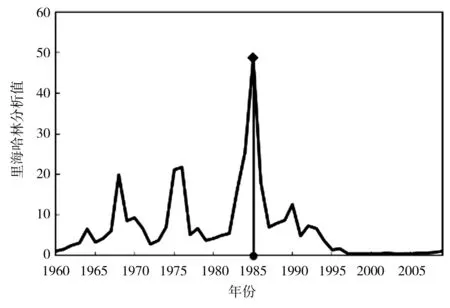
g)秋季里海哈林分析值

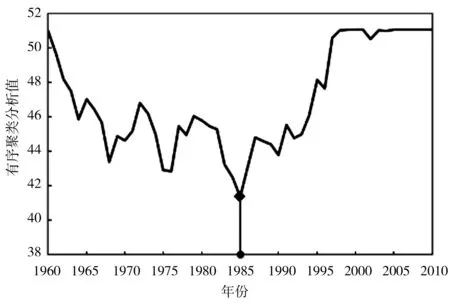
h)秋季有序聚类分析值

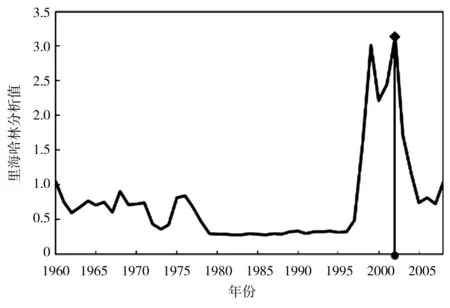
i)冬季里海哈林分析值

j)冬季有序聚类分析值

表10 CPBI突变点识别

4 结论与讨论

基于渭河华县站1960—2010年的水文气象资料，应用Copula联合分布函数构建了综合干旱指数CPBI，并选取单一指数与其比较验证CPBI的可靠性，在此基础上分析了渭河的干旱特征，结论如下。

a)综合降水和基流构建的新综合干旱指数CPBI能够同时表征气象干旱与水文干旱，且CPBI与SPI、SRI的相关系数较大，并通过游程理论分析后，CPBI表现出的干旱严重程度更强、历时更长，可以更好用于渭河的干旱检测和预警。

b)1960—2010年发生的严重干旱事件，主要由1978年前后的春季干旱、1997年的全年干旱和2000年前后的冬季干旱造成，由于季节原因，春季多发水文干旱，夏、秋季气象和水文干旱均发，冬季多发气象干旱。

c)渭河的CPBI在1960—2010年存在变异，春季为1994年，夏季为1993年，秋季为1985年，冬季未出现突变显著年份，年度为1975年，均存在于上述严重干旱高发时间段；1960—2010年，年和四季的CPBI呈下降趋势，且除冬季为不显著下降，其他均为显著下降趋势，说明渭河的干旱趋势仍往严重方向发展，应加强对极端干旱事件的防范。

较准确地分析了渭河的干旱特征，构建的综合干旱指数在渭河干旱监测中具有一定的实用价值，也为其他流域干旱评价提供了途径，有助于指导研究区域内防灾减灾，为有关部门提供更加可靠的决策依据，达到防治旱情的目的，有利于促进地区的可持续发展。

所构建的CPBI是基于气象和水文数据形成的，并未考虑农业和社会经济干旱，且使用的基流数据是基于数字滤波法分割出来的，未验证其他方法分割的基流的有效性，对构建的指数在渭河华县站的适用性进行了验证，可以进一步在其他流域验证适用性。