高强度开采地表损伤程度分类判别与控制研究

李晓斌，李全生,2,3,4，韩鹏华，许旭辉，皇甫龙

(1.中国矿业大学(北京) 能源与矿业学院，北京 100083；2.煤炭开采水资源保护与利用国家重点实验室，北京 102209；3.国家能源投资集团有限责任公司，北京 100011；4.北京低碳清洁能源研究院，北京 102211)

神东矿区是我国西部矿区高强度开采的典型代表，工作面具有埋深小、采高与开采尺寸大、推进速度快、开采设备机械化程度高等特征，覆岩破坏与地表损伤比较严重，容易产生大量覆岩裂隙与地裂缝[1-2]。高强度开采引起地下水资源系统发生剧烈变化，影响地表土壤水分、有机质与矿物质含量，加之西部地区自身生态环境脆弱，造成煤炭高效开采与生态保护的矛盾日益凸显[3-4]。因此，从工作面、覆岩与地表3个角度出发，研究高强度采动损伤定量评价与减损技术迫在眉睫。

采动损伤是指煤层开采后改变围岩应力状态，形成高地应力区域，导致覆岩发生变形、破坏与运移，最终传导至地表，产生开采沉陷和生态损伤的过程[5]。由此可见，采动损伤传导涉及煤炭开采的全生命周期。我国采矿科技工作者针对高强度采动损伤也开展了一系列研究，李全生[6]等从开采源头与采动损伤能量角度出发，建立高强度开采损伤传导模型，并在上湾煤矿12401工作面得到应用；何祥[7]等基于定义覆岩损伤度，探究了工作面长度与推进速度对覆岩损伤程度的影响；胡振琪[8]等基于现场实测数据，给出了风积沙区工作面埋深、推进速度与地裂缝发育周期的函数模型；此外还有众多采矿学者[9-11]以工作面开采参数作为指标，采用随机森林算法、层次分析法、遗传算法等数学方法对覆岩损伤高度与开采沉陷进行预测。上述研究主要集中在工作面开采参数对覆岩或地表损伤的影响，未将工作面开采参数、覆岩与地表损伤三者紧密联系起来，且鲜有研究涉及采动损伤程度定量评价与分类判别。目前，主要通过改变开采方法(限厚开采、条带开采、充填开采、采-充-留协调开采)、留设煤柱、覆岩离层注浆技术等控制采动损伤[12-15]。整体治理手段比较单一，部分方法实施成本较高、效率低，且损伤程度影响因素众多，不同开采条件下损伤程度与生态脆弱度不尽相同。在实际应用过程中，需针对具体地质条件，综合考虑各种采矿与生态环境因素，选取合适的控制方法，才能降低损伤程度，达到保护生态环境的目标。

鉴于此，笔者从工作面开采参数、覆岩硬度系数与地表松散层等方面建立PCA-DDA数学评价模型，借助主成分分析法获得高强度采动损伤类型，进一步通过距离判别分析法验证模型可靠性。根据采动损伤类型与现场采矿地质条件，在上湾煤矿12401工作面提出“大工作面快速推进法、覆岩局部注浆加固法与裂缝分区治理法”三步法，实现了源头减损(工作面)、传导过程(覆岩)、末端治理(地表)的开采全周期采动损伤控制。

1 神东矿区开采强度特征

神东矿区是我国最大的煤炭地下开采矿区，各煤矿主要集中分布在山西、陕西与内蒙，矿区分布面积广，东西方向宽度达55 km，南北方向长度可至90 km，已探明煤炭储量超过2 000亿t，同时具有上湾煤矿、补连塔煤矿、布尔台煤矿、大柳塔煤矿等千万吨大型矿井，整体产能在2 亿t以上。矿区煤层地质条件简单，埋藏较浅，工作面开采尺寸与采高大，推进速度较快，地表容易产生连续与非连续变形，整体开采强度比较大，神东矿区开采强度分布情况如图1[16]所示。

图1 神东矿区开采强度分布[16] Fig.1 Distribution of mining intensity in Shendong mining area[16]

2 主成分分析法与距离判别分析法原理

2.1 主成分分析法

由于高强度采动损伤程度影响因素众多，包括工作面开采参数，覆岩综合硬度与地表松散层厚度等，故引入主成分分析法(PCA)，它是将多个变量转化为几个综合指标的一种方法。在多变量分析过程中，经常由于变量多且变量间存在相关性，造成数据信息发生重叠。在维数较多的情况下，变量分析就变得更加复杂，且部分数据处理系统对指标数量有一定限制。主成分分析采用一种降低维度的办法[17]，通过求解几个主成分因子来最大程度地反映原有变量信息，且综合因子之间没有相关性，实现简化变量的目标，具体求解过程包括下述几个步骤。

2.1.1 相关系数矩阵

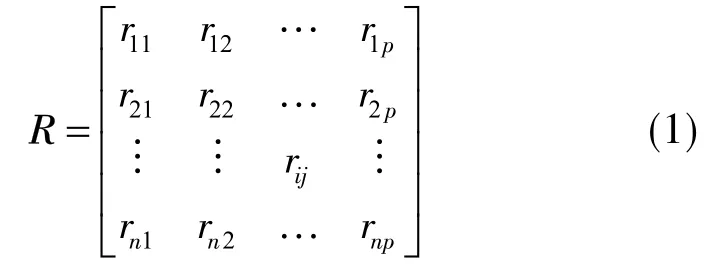
式中，R为相关系数矩阵；ri为原指标变量xi与yi之间的相关系数，其中，xi，yi为样本值。

ri的计算方法为

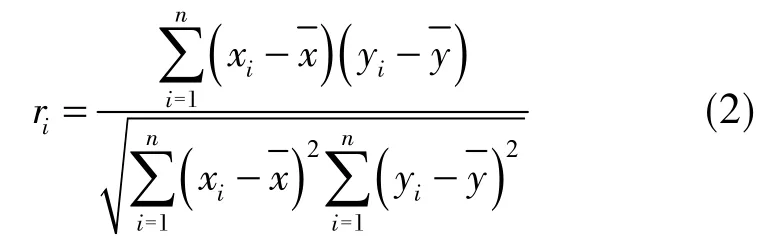
2.1.2 特征值和特征向量

相关系数矩阵R的特征方程为

式中，μ为特征值，取值为μ1，μ2，…，μp，且满足μ1≥μ2≥…≥μp；E为单位矩阵。

特征向量计算方法为

式中，α为特征向量。

根据式(4)求出特征值(μ1，μ2，…，μp)对应的特征向量值为α1，α2，…，αp。

2.1.3 主成分贡献率和累计贡献率

主成分贡献率计算方法为

式中，V为主成分贡献率；μi为第i个特征值；为p个特征值之和。

主成分累计贡献率计算方法为

式中，V′为主成分累计贡献率；为前i个特征值之和。

通常认为主成分累计贡献率超过85%，就可认定前m个主成分因子包括原有变量的绝大部分信息。μ1，μ2，…，μm对应第1，第2，…，第m个主成分因子，其中m≤p。

2.1.4 主成分因子载荷矩阵与主成分得分

主成分因子载荷计算方法为

式中，li为第i个主成分因子载荷；zi为第i个得分情况；αi为第i个特征向量值。

得到主成分因子载荷后，求解主成分得分矩阵G为

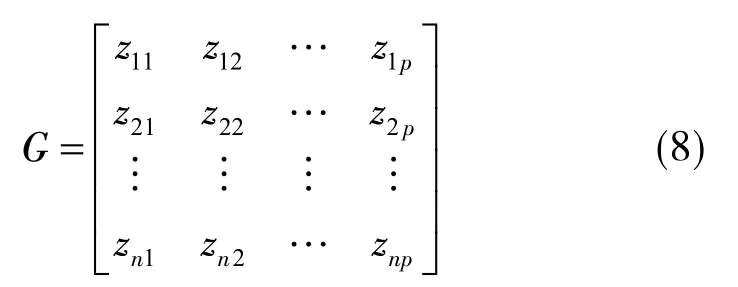
根据特征值与主成分因子得分，可求得综合得分，具体计算方法为

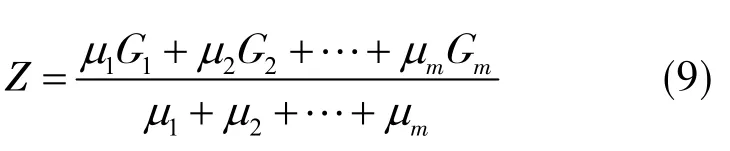
式中，Z为综合得分；G1，G2，…，Gm对应第1，第2，…，第m个主成分因子得分。

2.2 距离判别分析法

距离判别分析法(DDA)是根据多变量确定已有样本类别，用来判别未知样本类别的一种分析方法，通常用误判率来表示判别的可靠性[18]。假设Q1与Q2为2个不同总体，X1，X2，…，Xm是来自Q1的m个训练样本，Y1，Y2，…，Yn是来自Q2的n个训练样本，如果属于Q1的样本被误判为属于Q2的个数为u个，属于Q2的样本被误判为属于Q1的个数为v个，则误判率η可表示为

式中，u，v为误判样本数。

3 高强度开采损伤评价指标

煤层高强度开采后从直接顶开始上覆岩层逐次发生弯曲破断，采动损伤逐层由下向上传导直至地表，引起地表产生一系列连续与非连续变形，威胁西部脆弱的生态环境。鉴于此，高强度开采损伤评价指标体系的确定要包含工作面、覆岩与地表整个开采全周期。从工作面角度考虑，选取工作面宽度、工作面推进长度、采高、推进速度、埋深与宽深比等指标，覆岩方面引入覆岩硬度系数，地表方面包括松散层厚度与沙基比(松散层厚度与基岩厚度之比)。关于工作面开采参数对地表损伤的影响的研究较多，在此不再赘述。笔者重点研究松散层厚度、覆岩硬度系数与地表下沉系数之间的内在联系。

3.1 松散层厚度与地表下沉系数的关系

由于松散层具有力学强度与硬度小，容易跟随岩层发生流动的特征，在开采下沉过程中，松散层不仅能够减小覆岩综合硬度，还会增加覆岩载荷，促使采空区上方岩层处在高载荷应力中[19]。由于松散层的特性，在开采引起覆岩断裂时，会很快传导至地表，产生地裂缝等采动损害。如图2所示，基于高强度开采工作面部分数据拟合，结果表明松散层厚度与埋深比值与地表下沉系数呈二次函数关系，且在松散层厚度与埋深比值为0.25附近出现转折。

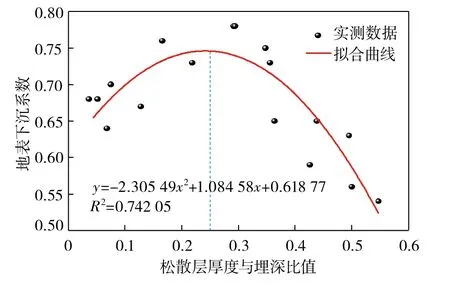
图2 松散层厚度与埋深比值与地表下沉系数的关系 Fig.2 Relationship between the ratio of loose layer thickness to buried depth and surface subsidence coefficient

这是由于当比值小于0.25时，没有形成松散层拱结构，松散层以载荷形式作用在基岩上面，随着松散层厚度增加，地表下沉系数增大；当比值大于0.25时，在厚度较大的松散层中形成拱结构，对地表下沉起到一定控制作用，地表下沉系数减小。

3.2 覆岩硬度系数与地表下沉系数的关系

覆岩硬度与岩石中所含矿物成分、岩石类型及单轴抗压强度等息息相关。在高强度开采条件下，坚硬顶板悬露面积大，不易发生垮落，当到达岩层的破坏强度时，覆岩发生切落式破坏，引起地表突然陷落。在覆岩硬度较小时，随着工作面的开采，地表逐渐出现缓慢式下沉。

覆岩硬度系数[20]计算公式为

根据式(11)可得K∈[0,1]，当K=0时，上覆全部为松散层；当K=1时，上覆全部为岩层；当K∈（0,1）时，煤层上方存在岩层与松散层互层。

图3为覆岩硬度系数与地表下沉系数的关系。由图3可知，在覆岩硬度系数较小时，地表下沉系数呈上升趋势；在覆岩硬度系数较大时，起到相当于关键层的作用，从而控制地表下沉的效果，地表下沉系数逐渐减小。

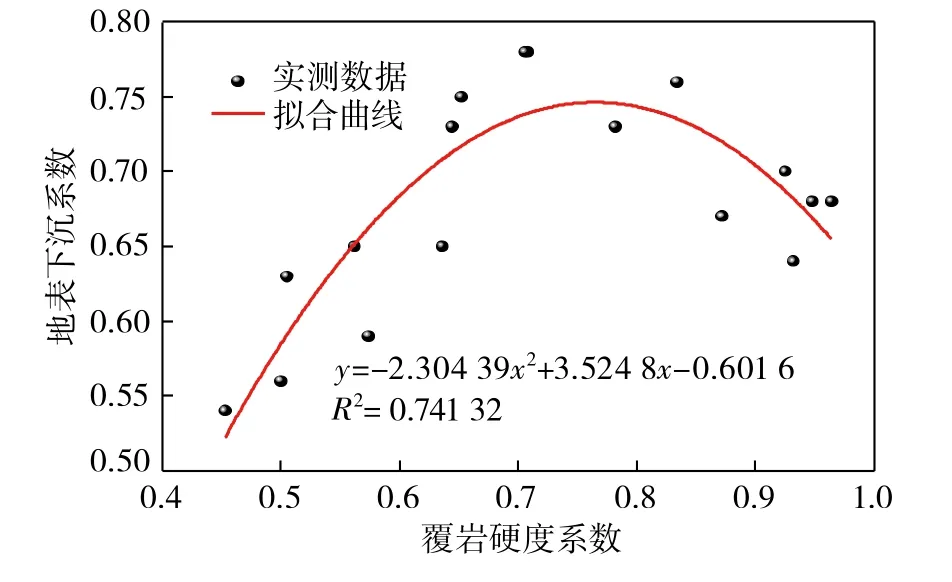
图3 覆岩硬度系数与地表下沉系数的关系 Fig.3 Relationship between overburden hardness coefficient and surface subsidence coefficient

4 数学评价模型的建立

通过收集神东矿区25个高强度开采工作面相关数据，对工作面开采参数、覆岩硬度系数、地表松散层厚度等数据进行了汇总，见表1。

4.1 Pearson相关系数矩阵的确定

由于各个指标量纲不同，在进行主成分分析之前，需要对原始数据进行标准化处理，将收集的数据导入DPS数据处理系统得到相关系数矩阵，见表2。

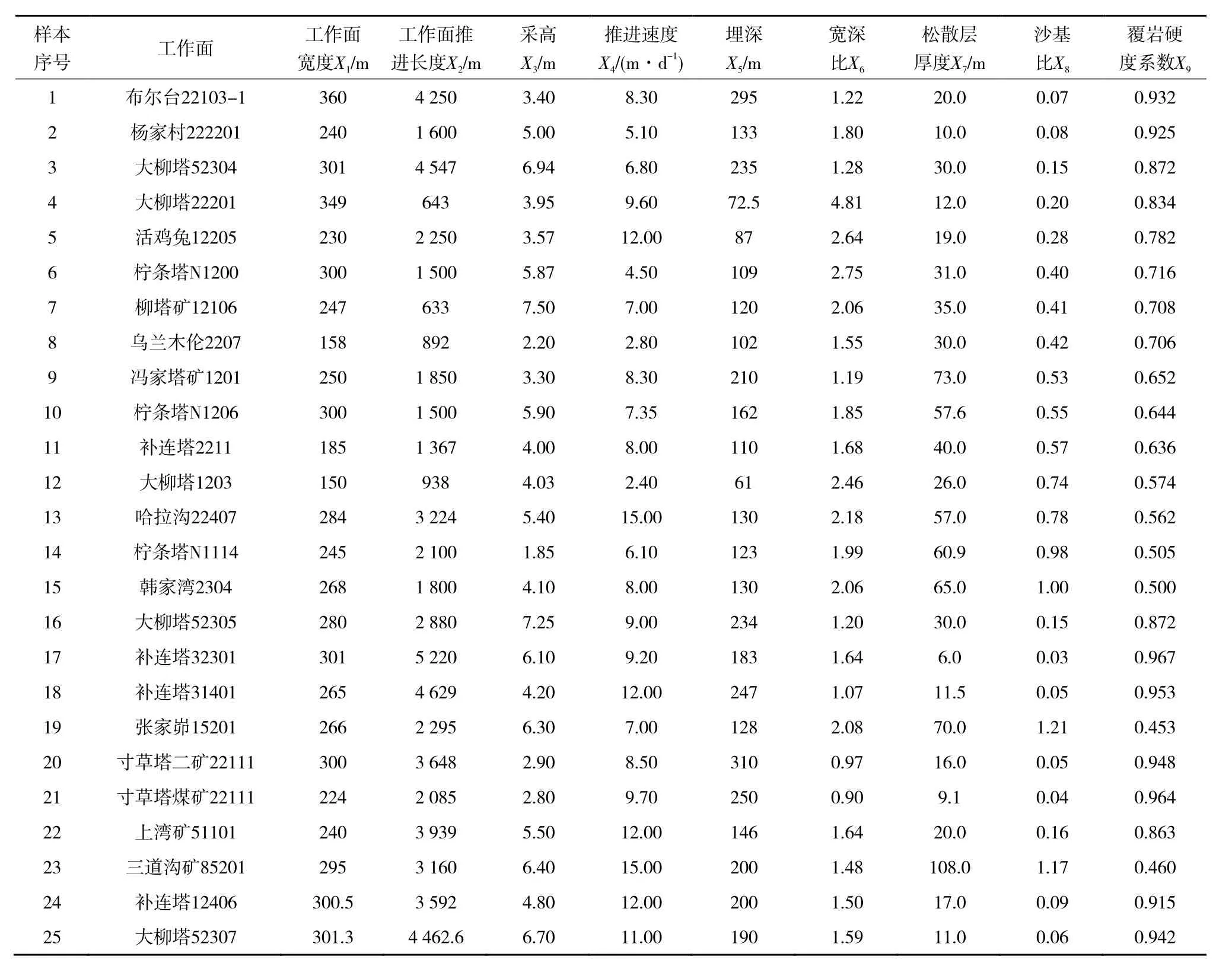
表1 不同采矿地质条件下高强度开采工作面数据 Table 1 Data of high-intensity mining face under different mining geological conditions

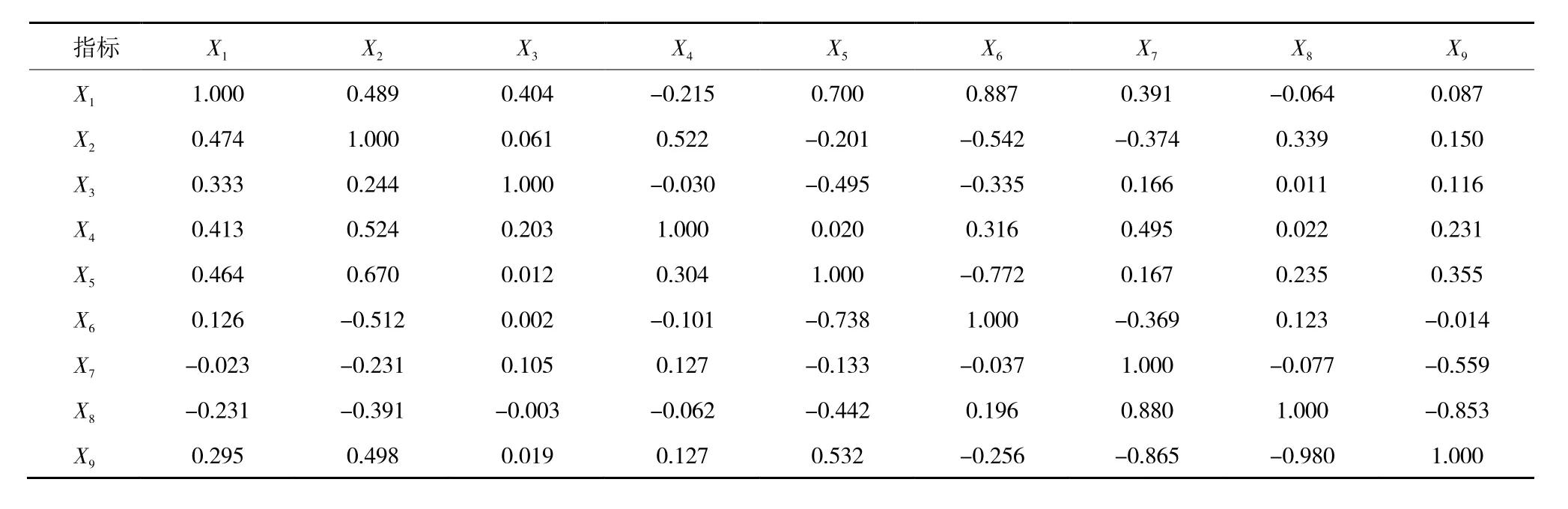
表2 Pearson相关系数矩阵 Table 2 Pearson correlation coefficient matrix

由表2可以看出，宽深比(X6)与工作面宽度(X1)相关系数为0.887，松散层厚度(X7)与沙基比(X8)、覆岩硬度系数(X9)相关系数分别为0.880，-0.865，覆岩硬度系数(X9)与沙基比(X8)相关系数为-0.853，这些变量之间存在显著性较高的相关关系，进一步反映原始指标彼此之间存在信息重叠的现象，因此很有必要运用主成分分析法对评价指标进行维度降低处理，获取新的互不相关指标。

4.2 主成分因子分析

运用Data Processing System(DPS)软件对数据进行主成分分析，得到KMO(Kaiser-Meyer-Olkin)检验值为0.526，大于0.500，Bartlett球形检验p=0，表明采用主成分分析法是可行的。特征值在一定情况下能够反映主成分对指标的影响程度。根据主成分分析法，选取累计百分率超过85%即能概括原变量的大部分信息，DPS系统默认取90%。特征值分布见表3。

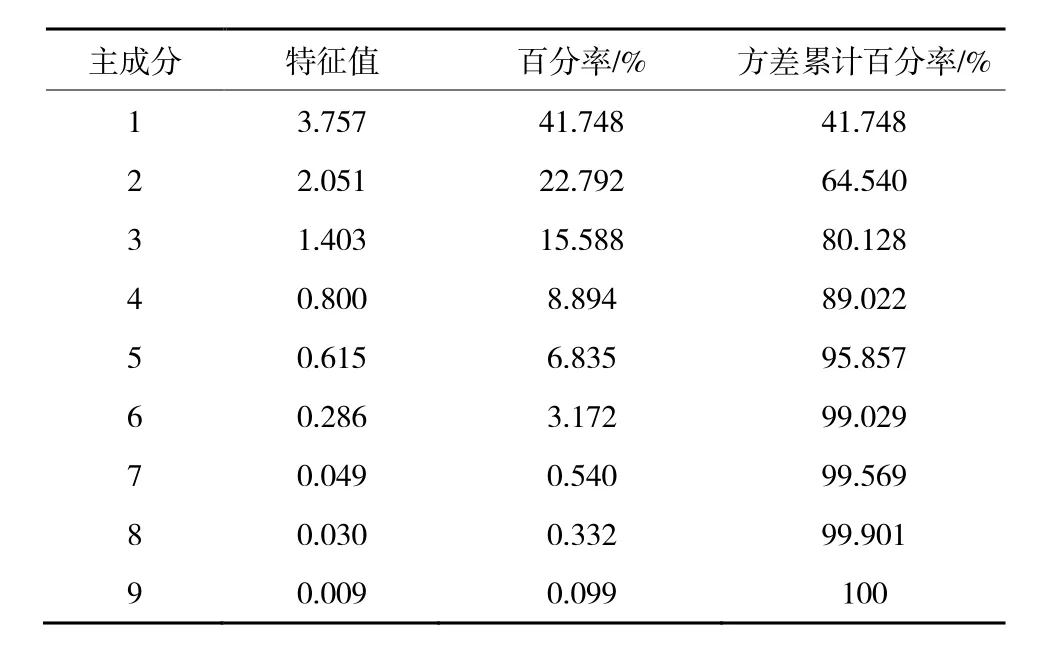
表3 特征值分布 Table 3 Distribution of eigenvalues

由表3可知，前5个主成分特征值分别为3.757，2.051，1.403，0.800，0.615，方差累计百分率为95.857%。由图4可知，当主成分数超过5，特征值逐渐趋向收敛状态。故选择前5个主成分能够较好地反映原有变量信息，即该5个主成分能解释原变量95.857%的内容。基于此，获得这5个主成分的因子载荷矩阵，见表4。

该矩阵揭示了主成分因子与原有变量之间的相关程度，矩阵中数值绝对值越大，表示主成分因子与原变量相关程度越高。第1个主成分因子与X9最相关，在很大程度上解释了覆岩硬度系数，从第2，3，4，5个主成分因子来看，X7(0.724)，X6(0.778)，X3(-0.737)，X4(-0.502)的绝对值最大，分别反映了与松散层厚度、宽深比、采高和推进速度的相关程度，其中推进速度的相关程度较小。

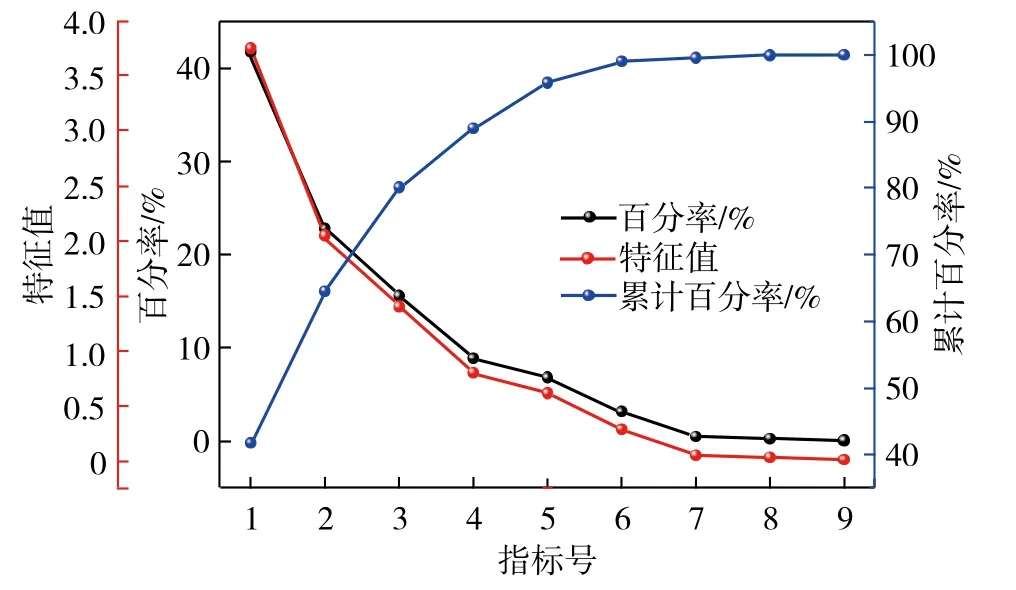
图4 主成分分析结果 Fig.4 Results of principal component analysis

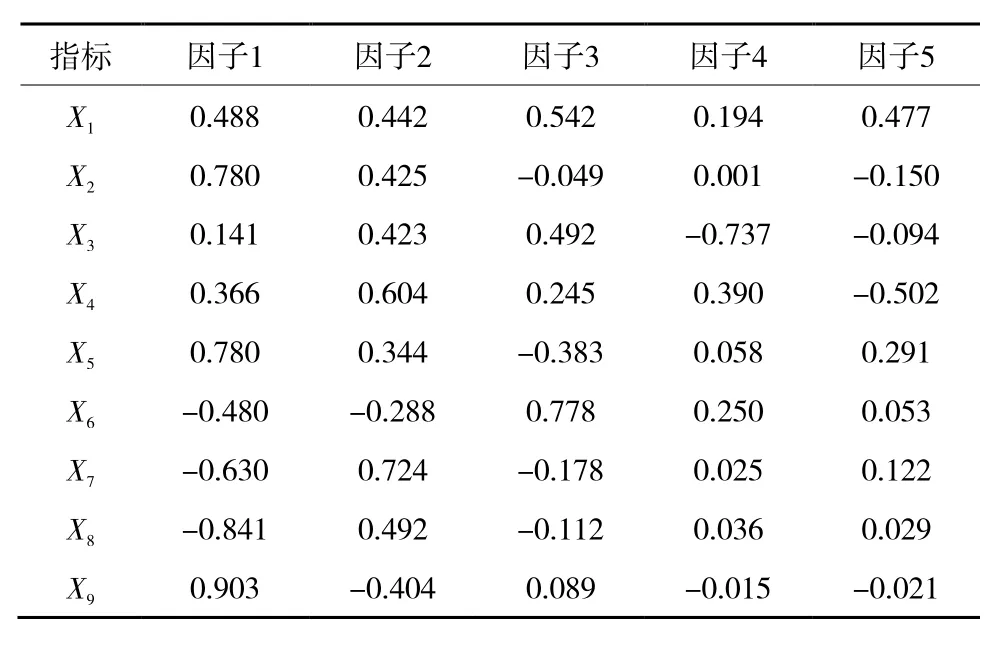
表4 因子载荷矩阵 Table 4 Factor load matrix

然而，从各个主成分因子反映的原变量来看，用单一主成分来确定高强度开采沉陷程度的大小是比较困难的，因此采用前5个主成分作为综合评估指标，以各个主成分方差贡献率为权重建立综合评价数学模型[21]为

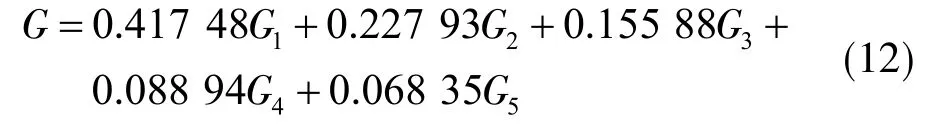
基于综合评价数学模型，获得表1中25个工作面高强度采动损伤程度的排名情况，见表5。

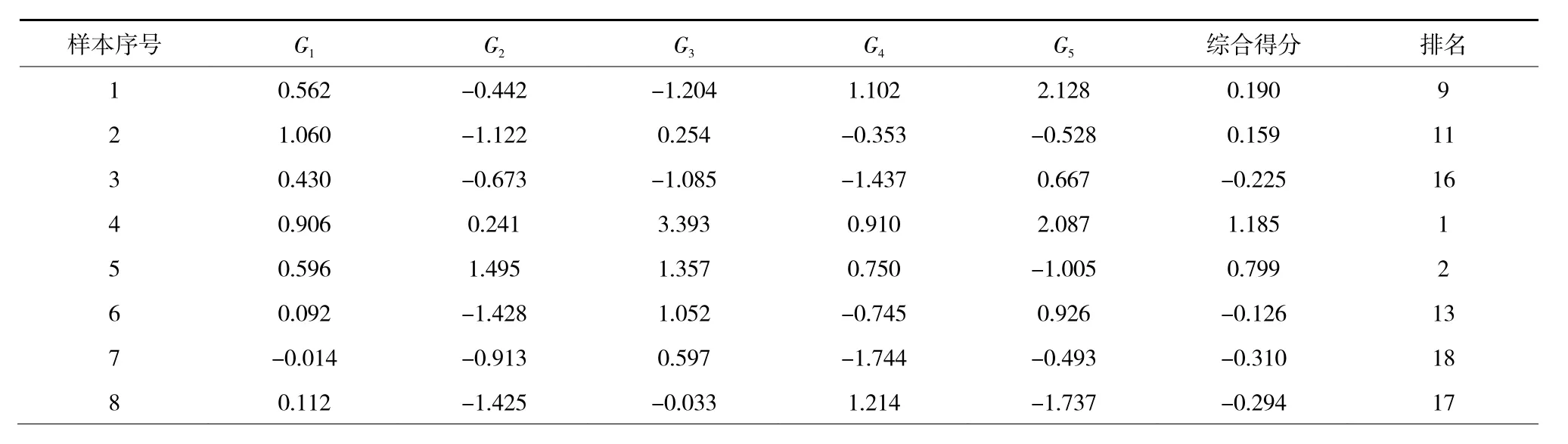
表5 高强度开采损伤程度综合得分与排名 Table 5 Comprehensive score and ranking of damage degree of high-intensity mining

续 表

根据排名与综合得分情况得到图5，将高强度采动损伤分为Ⅰ型、Ⅱ型、Ⅲ型、Ⅳ型，分别对应极高、高、中、低4个损伤程度，其中Ⅰ型包括4，5，24，18，22样本组，综合得分＞0.5；Ⅱ型包括17，25，21，1，20，2，13样本组，综合得分0～0.5；Ⅲ型包括6，16，11，3，8，7，12，14样本组，综合得分-0.5～0；Ⅳ型包括10，15，9，23，19样本组，综合得分＜-0.5。此方法可实现高强度开采损伤程度的定量判别，为地表损伤治理与生态修复提供科学指导。

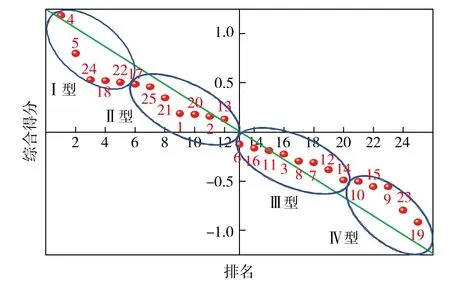
图5 综合得分与分类 Fig.5 Comprehensive score and classification chart

4.3 数学模型验证

采用DDA对定量分类结果进一步验证，以PCA定量评价得到的Ⅰ型、Ⅱ型、Ⅲ型、Ⅳ型作为4个不同总体，学习样本选取图中25组散点数据，同时为降低训练样本与测试样本个数对分类结果的影响，取测试样本占学习样本的20%，选择5组情况进行学习，训练样本与测试样本比例分别为24∶1，23∶2，22∶3，21∶4，20∶5，见表6。当训练样本与测试样本比例为23∶2，误判概率最大为4.35%，可能与样本数量少、指标选取不全面、模型泛化能力不强等因素有关，但该模型整体判对概率超过95%，表明在高强度开采损伤程度评价方面是可行的。

表6 不同样本比例的5组学习情况 Table 6 Learning of 5 groups with different sample proportions

5 现场应用

5.1 工程背景

以神东矿区上湾煤矿12401工作面为工程背景，工作面宽度300 m，推进长度5 429 m，采高8.6 m，平均推进速度13.6 m/d，埋深184 m，宽深比1.63，松散层厚度62 m，沙基比0.51，覆岩硬度系数0.663，采用PCA-DDA数学模型判定采动损伤类型为Ⅱ型，相应损伤程度为高。由于开采强度较大，地表损伤控制层发生破断，传导至地表产生大量地裂缝及塌陷槽，图6[22]为地裂缝分布平面图，不同颜色代表不同裂缝宽度。

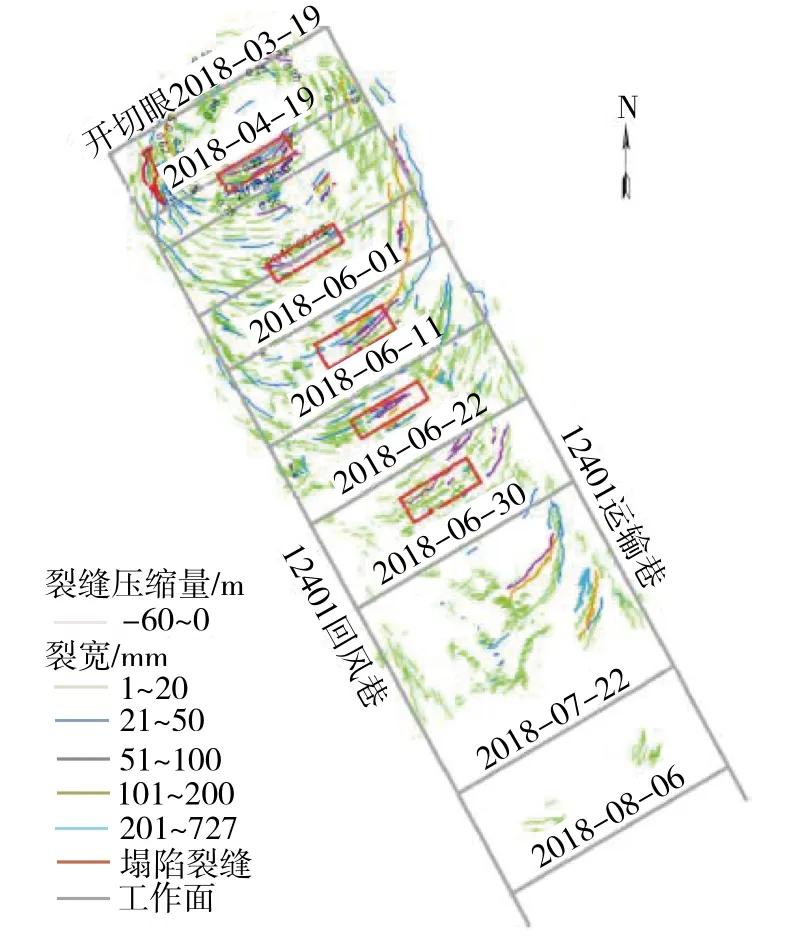
图6 地裂缝分布平面[22] Fig.6 Ground fissures distribution plan[22]

5.2 高强度采动损伤控制

针对上湾煤矿12401工作面地表损伤程度较高的特点，综合采用大工作面快速推进法、覆岩局部注浆加固法与裂缝分区治理法，实现了源头减损(采场)、传导过程(覆岩)、末端治理(地表)的开采全周期采动损伤控制。

5.2.1 大工作面快速推进法

大工作面采动影响范围内地表变形很小，该工作面在开采初期处于设备调试阶段，平均推进速度＜4 m/d，覆岩及地表损伤严重，后期平均推进速度达到13.8 m/d，覆岩卸压不充分，基本顶来压步距增加，在时间和空间上损伤传导表现出一定滞后性，损伤程度有所减小。

图7[7]为不同推进速度下地表中部裂缝发育情况，表明加快推进速度可使地表损伤程度更为缓和。

图7 不同推进速度下地裂缝发育特征[7] Fig.7 Development characteristics of ground fissures at different advancing speeds[7]

5.2.2 覆岩局部注浆加固法

覆岩局部注浆加固法是通过在采空区垮落带与离层裂隙带注浆实现的，垮落带注浆能够维持基本顶稳定性，减小顶板下沉量与垮落带上方岩层移动变形程度。离层裂隙带注浆可以支撑关键层的下沉，进一步加固关键层，将采动损伤阻隔在覆岩中，降低覆岩破坏高度，促进“三带”模式的出现，减弱地表损伤程度。

图8为注浆前后裂缝宽度随时间的变化曲线，由图8可知注浆后裂缝发育更加平缓，裂缝宽度显著减小，能有效实现采动损伤控制。

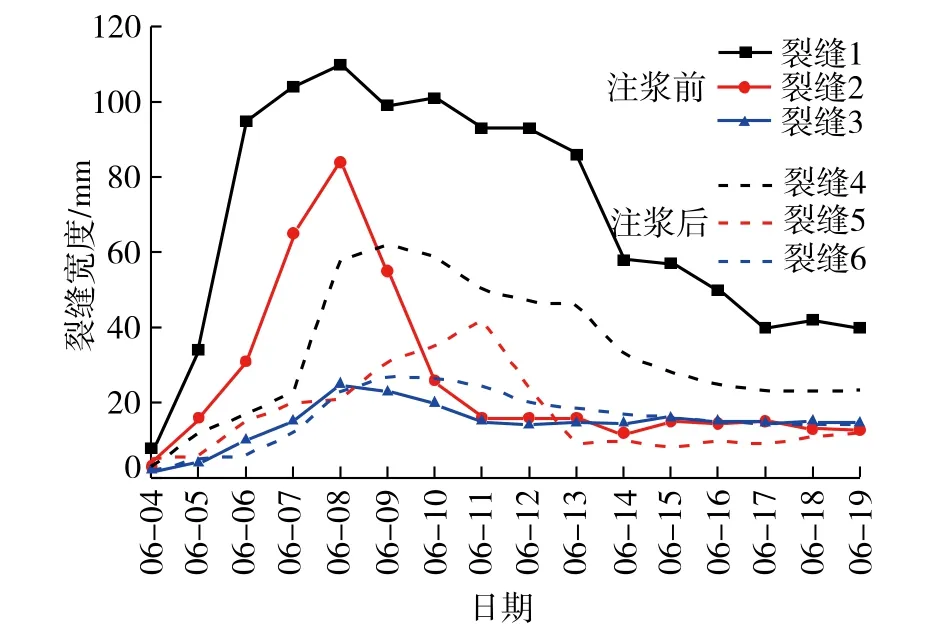
图8 注浆前后裂缝宽度变化特征 Fig.8 Variation characteristics of fracture width before and after grouting

5.2.3 地裂缝分区治理法

针对开采边界永久裂缝采取源头减损与加固关键层的控制方法，对于中部动态裂缝，由于关键层破断岩块回转，能闭合的裂缝让其自修复，对于不能闭合的裂缝采取人工填埋的方法。

6 结 论

(1) 基于工作面开采参数、覆岩硬度系数与地表松散层厚度等9个评价指标，提出一种高强度采动损伤定量评价数学模型——PCA-DDA模型，该模型可以在保留原变量信息的情况下，转化5个主成分因子分析，实现高强度采动损伤定量评价与分类判别，模型判对概率高达95%以上。

(2) 基于PCA-DDA模型，得到高强度采动损伤程度的排名与综合得分情况，在此基础上将高强度采动损伤分为Ⅰ型、Ⅱ型、Ⅲ型、Ⅳ型，分别对应极高、高、中、低4个损伤程度，此分类结果为采动损伤治理与生态修复研究提供科学指导。

(3) 将PCA-DDA模型应用于上湾煤矿12401工作面，结果表明该工作面采动损伤程度较高，综合采用大工作面快速推进法、覆岩局部注浆加固法与裂缝分区治理法，实现了源头减损(工作面)、传导过程(覆岩)、末端治理(地表)的开采全周期采动损伤控制。

需要说明的是，由于数据来源有限，笔者只针对部分高强度开采工作面及评价指标初步建立数学分类判别模型，没有考虑其他因素的影响，如导水裂隙带发育高度、关键层位置及数量、地裂缝参数等，其将在后续工作中做进一步研究。