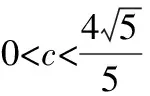活用数学思想解题 促进学生深度学习

◎邱宏毅

(福建省漳浦县锦屿学校，福建 漳州 363210)

数学思想是数学的精髓，是学生获取数学知识、发展思维能力的重要工具，是解决数学问题的有效方法，是数学方法与技能固化升华的体现.课程标准明确指出：通过义务教育阶段的数学学习，学生能体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式思考，增强发现和提出问题的能力、分析和解决问题的能力.在初中数学教学过程中渗透数学思想可让学生经历数学思考，对开发、拓展学生的解题思路将产生深远的意义.它能使学生从本质上把握数学知识，优化思维品质，学会运用数学思想分析问题、解决问题，为今后进一步学习数学奠定良好的数学思维基础.数学思想渗透于初中数学的各个阶段，常见的数学思想有方程思想、数形结合思想、分类讨论思想、转化与化归思想等，其分布和体现形式更是分散的，因此，笔者认为，通过对初中数学教材内典型例题及近年来全国各地中考真题的分析、解答，以理论结合实例的形式进行归纳、总结、梳理、点拨，能使学生从中领会数学思想的迁移应用，理解数学思想在初中数学解题中的应用，引导学生形成更高维度的认知，促进学生深度学习，发展高阶思维，培养学生科学、系统、严谨的解题思维.

数学深度学习的主要特征为：主动理解与批判接受，激活经验与建构新知，知识整合与深层加工，把握本质与渗透思想，有效迁移与问题解决.下面将通过具体的例子剖析如何灵活应用数学思想解题，促进学生深度学习的真正发生.

一、活用方程思想，促进学生深度理解数量间的关系

方程思想是对于一个问题用方程进行解决，一般是从分析问题的数量关系入手，将问题中的未知量和已知量之间的数量关系通过适当设未知数构建方程(组)，或利用方程(组)的性质去分析、转换、解决问题的思维方式.用方程思想解题的关键是利用已知条件或公式、定理中的已知结论构造方程(组).灵活应用方程思想，有利于学生对各种数量间关系的深度理解.

例1如图1，有一个直角三角形纸片，两直角边AB=6 cm，BC=8 cm，现将直角边BC沿直线BD折叠，使点C落在点E处，求△BDF的面积是多少.

图1

分析由折叠的性质可得△BDC与△BDE全等，进而得到对应边相等、对应角相等，再由两直线平行内错角相等、等量代换及等角对等边，得到FD=FB，设FD=FB=xcm，则AF=(8-x)cm，在Rt△AFB中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出FD的长，进而求出△BDF的面积.

解由折叠，可得△BDC≌△BDE，

∴∠CBD=∠EBD，BC=BE=8 cm，ED=DC=AB=6 cm.

∵AD∥BC，

∴∠ADB=∠DBC，

∴∠ADB=∠EBD，

∴FD=FB.

设FD=FB=xcm，则有AF=AD-FD=(8-x)cm.

在Rt△ABF中，根据勾股定理，得x2=(8-x)2+62，

评析在解决几何折叠的面积问题中，若用线段直接进行运算较为复杂，而利用方程思想求解则较简捷方便.本题主要借助未知量，在直角三角形中利用勾股定理建立三边之间的代数关系，利用方程较好地解决相关的线段长度计算问题，这样处理有利于学生深度理解和把握几何问题中的数量关系，提升分析问题和解决问题的能力.

二、活用数形结合思想，促进学生深度掌握数形转化技能

数形结合就是将代数问题与图形结合起来分析研究题目，数是形的抽象概括，而形是数的直观体现，它可以把抽象的数转化为直观的形，也可以把复杂的形转化为具体的数.加强训练学生应用数形结合思想解题，对其巩固数学基础知识、培养良好的解题思维、提高解题能力尤其是转化能力至关重要.

1.以“形”求“数”

例2如图2所示，点P是∠α的边OA上一点，且P点的坐标为(4，3)，求sinα和cosα的值.

图2

分析根据锐角三角函数的定义，可构造含有∠α的直角三角形，再根据定义求解.

解如图2，过点P作PQ⊥x轴于点Q，则△POQ为直角三角形.

由P(4，3)，可得OQ=4，PQ=3，

评析本题无法直接通过数值计算sinα和cosα的值，而由图形上点的坐标去确定对应线段的数值，则可直接计算，这是由“形”得“数”的具体表现.通过这种数形结合的教学，学生能较好地理解锐角三角函数定义的实质，更能深度理解把几何图形的性质转化为数量关系的作用，通过代数方法解决几何问题，增强学生解题的转化能力.

2.以“数”解“形”

答案D

评析由于二次函数y=ax2+bx+c(a≠0)的性质及其图像是由系数a,b,c共同决定的，因此要判断图像的大致形状，只需要确定系数a,b,c的值或符号即可，这是由“数”得“形”的具体表现，充分体现了数与形的统一.这类试题的训练有利于学生对抛物线的性质及其图像中数形关系的深度理解，提升其转化与化归能力.

3.“数”“形”结合

有类问题，题中用字母表示几何图形中的线段长，这本身就是数形结合了，再通过某种等量关系，如面积、周长及它们的和差倍分等关系，确定这些线段之间的关系式，经过这样的分析处理，学生能更深层次地把握几何图形与代数式(或关系式)的联系，化几何的演绎推理或演算为代数计算，也能更好地理解借助函数图像如何把几何中复杂的线段关系直观化，增强知识间的整合与深层加工能力.

例4如图3，河旁有一座小山，从山顶A处测得河对岸点C的俯角为30°，测得岸边点D的俯角为45°，又知河宽CD为50 m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC，求缆绳AC的长.(结果保留根号)

图3

分析本题需要利用直角三角形的边角关系进行求解，可以作AB⊥CD，交CD的延长线于点B，这样得到两个直角三角形Rt△ABC和Rt△ABD，且∠ACB=∠CAE=30°，∠ADB=∠EAD=45°.若设AB=x，则根据直角三角形的边角关系，可以用含x的代数式分别表示出CB和BD的长，利用BC-BD=CD这个等量关系可以列出关于x的方程，并求出x，从而求出AC的长.

解作AB⊥CD，交CD的延长线于点B.

在Rt△ABC中，

∵∠ACB=∠CAE=30°，∠ADB=∠EAD=45°，

∴AC=2AB，DB=AB.

设AB=x，则BD=x，AC=2x，CB=50+x.

∴AB=CB·tan∠ACB=CB·tan 30°.

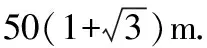
评析本题运用“数”“形”结合法，灵活地应用解直角三角形的有关知识解决生活中的实际问题.解决此类问题一般是通过画图、作辅助线构造直角三角形，并合理地设元、建立方程进行解决，体现了“数”“形”结合在解决几何问题中的重要应用.

三、活用分类讨论思想，促进学生提升发散性思维能力

深度学习要求学生克服已有经验的束缚，实现在原有知识、经验基础上的主动建构，在新情境中批判理解、迁移应用.分类讨论思想就是根据所研究对象的性质差异，分各种不同的情况予以分析、批判，再加以解决.分类讨论时应注意以下三个问题：(1)要弄清楚引起分类讨论的原因；(2)要确定分类讨论的对象和标准，标准不同，分类的结果也不同；(3)分类讨论的原则是不重复、不遗漏.

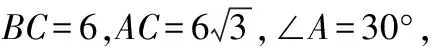
分析本题需将斜三角形转化为直角三角形，再利用直角三角形的边角关系进行求解.解题时需考虑两种情况：一是△ABC为锐角三角形，二是△ABC为钝角三角形.

解(1)若∠B是锐角，如图4所示，过点C作CD⊥AB于点D.

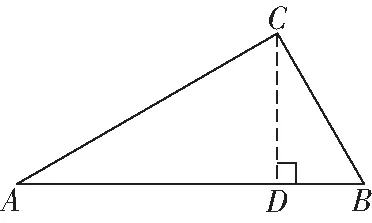
图4

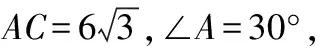
∴AB=AD+DB=9+3=12.

(2)若∠B是钝角，如图5所示，过点C作CD⊥AB,交AB的延长线于点D.

图5

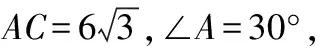
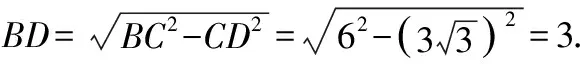
∴AB=AD-DB=9-3=6.

评析本题属于已知两边及其中一边对角求解三角形的问题，没有明确图形的形状，直接求解易出错，因此，这类问题往往要对三角形的形状进行讨论.对这类问题进行训练有助于学生对问题的批判理解、迁移应用，提升分析问题和发散思维的能力，以及对数学问题严密性的深入理解与掌握.

四、活用转化与化归思想，促进学生提升综合运用能力

深度学习强调探究式学习，在探究式学习中，一般由简单直观型知识结构向拓展抽象型知识结构延伸，逐渐完善个人数学知识体系，通过活用数学思想分析、解决问题来发展高阶思维能力，并有效迁移应用到解决真实情境问题中.深度学习着重研究解题思维的自然性，通过观察、分析、联想、类比等进行深度探究，运用转化与化归思想将实际问题数学化、陌生问题熟悉化、抽象问题具体化、复杂问题简单化，对所学知识做到有效的迁移应用，最后顺利解决原问题.

1.化动为静，巧解动态问题

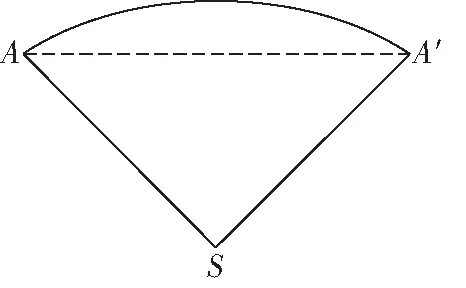
例6如图6，在平面直角坐标系中，若点P的坐标为(4，0)，⊙P交x轴于原点O和点N，A，B，C三点的坐标分别为(-2，0)，(0，6)，(0，c)，且0

图6

分析分析直线AC与⊙P的位置关系，可以优先考虑相切这种特殊关系，运用切线的性质定理求得c的值，此时c的值就是一个分界点.在解题的过程中，应用直线的“静态”——直线与圆相切作出图形，化动为静，这是解答本题的关键.

解当点C在线段OB上移动时，直线AC与⊙P有三种位置关系：相离、相切、相交.

设当点C运动到OB上某处时，恰使直线AC切⊙P于点M，连接PM.

∵AM是⊙P的切线，

∴PM⊥AM，且PM=4.

在Rt△APM中，AP=6，PM=4，

评析本题中，直线AC是运动状态的，要直接判断它与⊙P的位置关系不易，因此考虑化“动”为“静”，而且为准确定性，又化“形”为“数”，从而取得“化难为易、化繁为简”的效果.这类问题的训练有助于提升学生对动态问题的分析与解决，使其更深入地理解数与形、动与静的关系，对所学知识做到有效的迁移应用.

2.化曲面为平面，巧求最短距离

例7如图7，已知圆锥底面半径OA=10 cm，母线SA=40 cm，问：由点A绕侧面一周的最短距离是多少？

图7

分析如何绕圆锥侧面一周才能使路线最短，这难以想象，但是如果把圆锥的侧面展开，将曲面转化成平面，由“两点之间线段最短”则可求出最短距离.

解将圆锥的侧面展开可得到如图8所示的扇形，连接AA′，则AA′为点A绕侧面一周的最短长度.

图8

设圆锥侧面展开图的圆心角度数为n°，

∵OA=10 cm，∴圆锥底面周长为2π×10=20π(cm)，

∴△AA′S是等腰直角三角形，

评析空间中求最短距离对学生而言是陌生的，是不直观的，因此，可利用侧面展开图求圆锥侧面上两点间的最短距离，把空间图形转化为平面图形，达到化陌生问题为熟悉问题的目的，这也更符合学生的认知习惯.这类问题的训练有助于学生对新知识的深入探究和学习.

数学深度学习的关键是让学生在学习的过程中深化理解知识、发散思维、优化思维、提升思维，促进学生高阶思维能力的发展.任何数学问题的最终解决都是以数学思想为指导，以数学方法为手段，所以，有效地将数学思想纳入基础知识范畴，适时对数学思想和方法进行揭示、概括和强化，让学生从数学思想的高度把握知识的本质和内在的规律，逐步体会数学思想的精神实质，是促进学生深度学习、提高学生思维品质的重要举措.