基于动力学找形方法的非连续多重曲面拓扑重构研究
袁潮,张啸,邱松
基于动力学找形方法的非连续多重曲面拓扑重构研究
袁潮,张啸,邱松
(清华大学,北京 100084)
通过重拓扑高效地将工业建模工程中的多重曲面(B-rep)文件转化成均匀连续的网格(Mesh)文件,为参数化设计、有限元分析工作提供对接桥梁,形成参数化设计工作流闭环。基于Rhino平台下的算法插件,将预设有杆件弹簧力、边界锚固力、目标吸引力等约束的基础网格,包覆到已知多重曲面上,并通过动力学算法多次迭代收敛,将重拓扑网格无限趋近于原曲面,最终重构为均匀连续、网格数可控的四边网格。经过此工艺流程后,设计师只需几步点选操作,在几分钟内即可对非连续多重曲面进行重拓扑工作,获得的新网格均匀连续,且面数可控,省去了大量人力修复时间。通过动力学算法的重拓扑工艺,可使参数化设计师更顺畅地对接工厂,同时使有限元分析辅助支持设计更具效率,是工业设计数字闭环的重要技术基础之一。
动力学找形;重拓扑;参数化设计;网格映射;有限元分析;数据闭环
在工业生产中广泛存在着使用参数曲面进行表示的模型[1],如基于NURBS连续曲面或实体建模的表示方法[2],这类模型表示方法能很好地保存曲面的连续性信息。然而,在前期设计优化阶段,这类建模方式却远远达不到网格建模的高效性。网格建模以离散化方式逼近连续曲面,虽然不具备NURBS曲面的连续性,但是在大多数不需要很高连续性要求的工业生产中,网格建模在表达复杂曲面及纹理细节时更具实用价值。同时,随着计算性设计时代的到来,设计与数据的关系越发紧密,不论是外部数据的导入,还是对模型进行有限元分析,都需要将多重曲面(B-rep)转换为网格文件(Mesh)[3]。虽然市场现有的重拓扑工具很多,但是大部分集中在计算机动画领域或数字雕塑领域,很难与现有制造业建模水平匹配,而且强行使用这些平台进行重拓扑工作也需要人力进行曲面连续性的优化预处理,同样费时费力。在计算机图形学领域针对网格划分问题已有许多基础方法[4],如Delaunay法[5],波前法[6],映射法[7]等。一些研究者针对建筑领域的形态也做过一些研究,如基于引导线偏移的方法[8],针对建筑地板的拓扑连锁结构研究[9],对自由形式网架结构的研究[10],基于拓扑结构优化的生物形态建筑研究[11]等,但是这些方法并不完全适用于工业产品领域的形态重拓扑研究,况且相较于建筑形体,工业产品的形态往往更加复杂,同时对连续性及误差精度等要求更高,因此,在建筑上优化的一些方法并不能很好地适用于工业产品形态的重拓扑。针对工业生产领域中表面纹理的制作,此次研究提出了一种基于动力学找形的方法将NURBS曲面模型进行重拓扑网格化并进行纹理制作的方法。
1 基本原理
1.1 曲面的拓扑结构分类
该工作流基本原理如下:首先需要操作者对拓扑几何有非常基础的认识,对已知曲面进行分类,可分为单一曲面(Surface)和多重曲面(B-rep)。其中单一曲面包括开放的单一曲面(Open Surface)和封闭的单一曲面(Closed Surface)。多重曲面包括开放的多重曲面(Open B-rep)和封闭的多重曲面(Closed B-rep)。针对目标几何的开放性进行分类,并分别进行设计。几何形体的类型见图1。
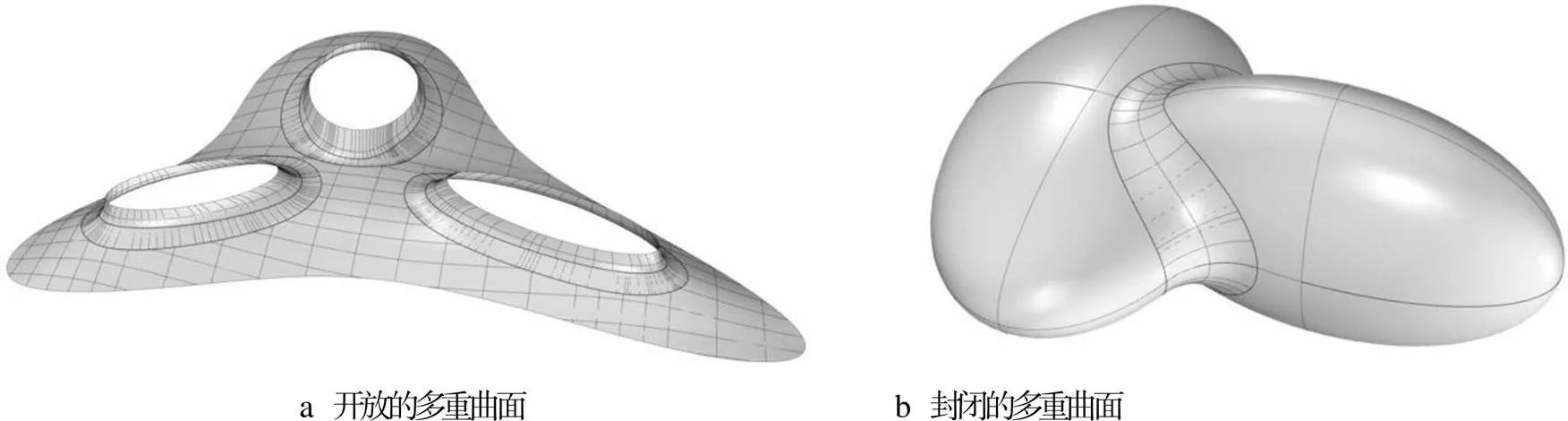
图1 几何形体的类型
1.2 基本拓扑网格单元设计
以“斯坦福兔”模型为例,在曲面分类中可被定义为“封闭的多重曲面”。其基本拓扑模型就是球体网格模型,不论其细节多烦琐,都可以抽象为球体表面网格顶点的拓扑关系,见图2。以一双运动鞋的鞋底模型为例,其在曲面分类中可被定义为“开放多重曲面”,其基本关系可通过一个平面网格进行概括,不论其底部是否凹凸,都可抽象为平面网格上各顶点的坐标变化,见图3。
对于目标模型,其开洞(亏格)情况是最重要的拓扑要素,基础网格模型必须对开口信息进行描述,见图4。重拓扑工艺操作人员需对目标几何有拓扑结构认知能力,并用简单网格来概括目标模型。针对网格细分等操作,可以使用建模软件内置的网格细分算法指令来完成,也可用插件(如Weaverbird)[12]完成。基础网格设计是一项类型概括工作,可以为计算机后续工作提供基本优化方向。

图2 斯坦福兔几何形体的拓扑关系
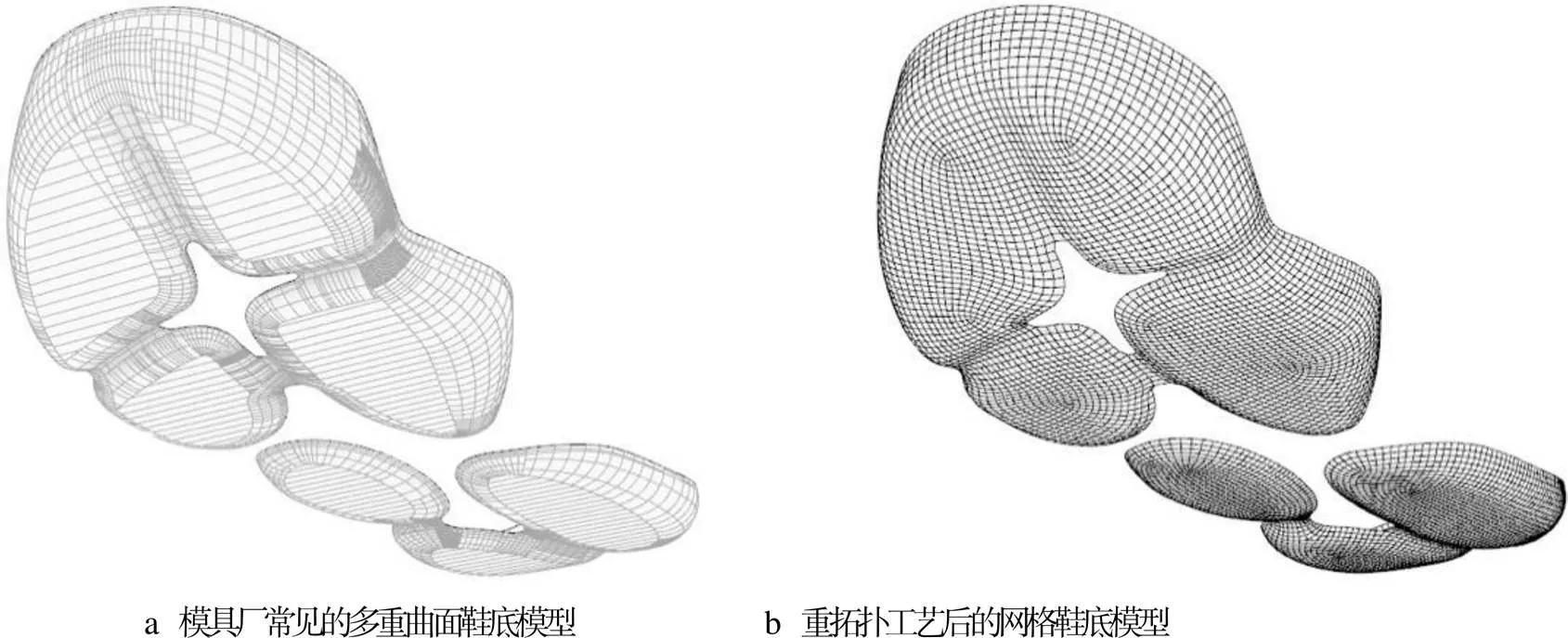
图3 鞋底几何形体的拓扑关系
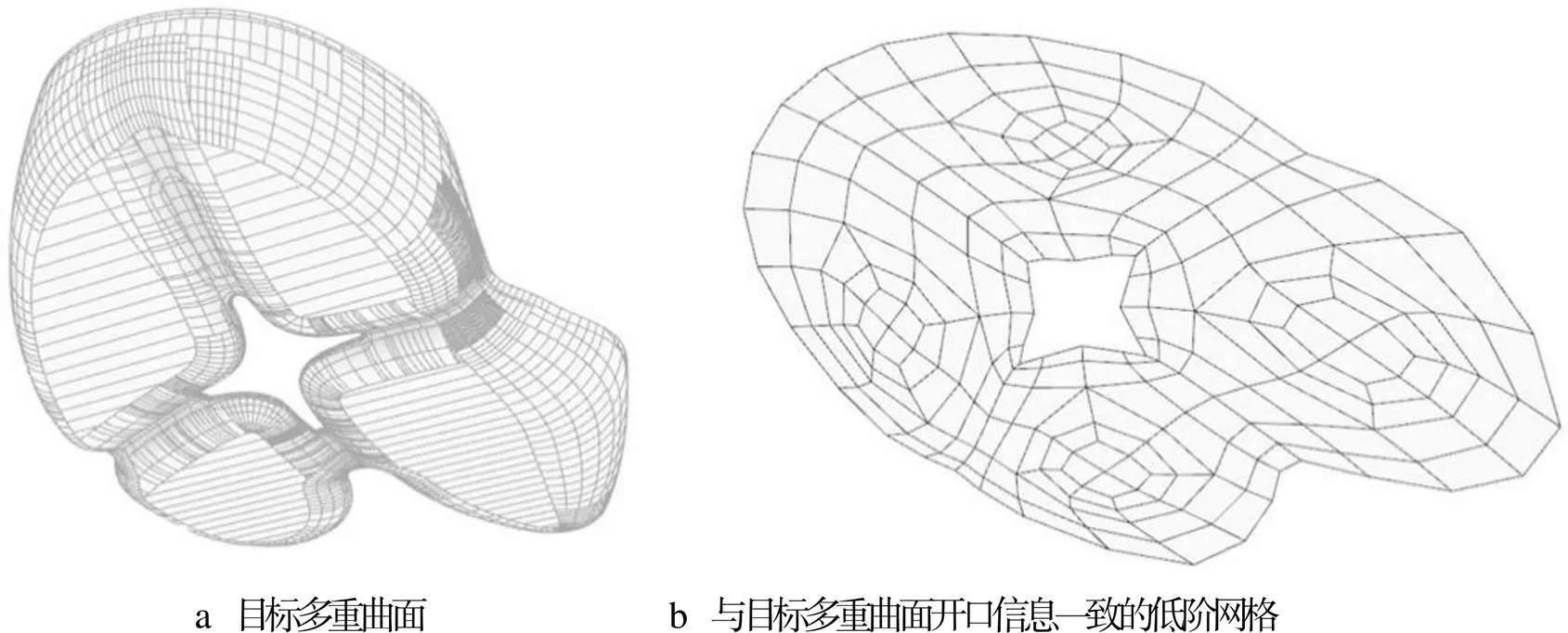
图4 几何形体的开口信息
1.3 动力学拟合找形
文中使用的动力学找形方法是基于Rhino平台下的可视化编程平台Grasshopper中的一款名为Kangaroo的力学模拟仿真插件,见图5。该插件可直接在Grasshopper中进行交互式的力学模拟、力学优化与力学找形。该插件由Daniel Piker开发制作,可免费用于商业和非商业项目中。目前最新的Kangaroo2已经内置于Rhino6的Grasshopper中。此插件可将网格文件中的点、线赋予不同的力学约束,在此项目中,笔者将网格边缘顶点定义为“锁定在目标边缘上”,以保证重拓扑的网格与目标多重曲面的边缘严格贴合;将网格内部的线定义为“彼此约束的弹簧力”,以防止在拟合过程中各点位置移动过大,而导致网格不均匀;将网格内部顶点定义为“向目标几何的吸引力”及“球体弹性碰撞力”,吸引力可以保证重拓扑网格严谨地吸附在目标曲面上,弹性碰撞力可以防止网格出现自折叠现象,影响最终网格平滑度。Kangaroo算法会逐渐向一个稳定解收敛,一般需要数十秒的等待,最终收敛到一个稳定态。

图5 动力学找形阶段用到的核心力学模拟单元
1.3.1 受力分析
具体而言,网格每个顶点所受到的力可分为杆件弹力、球体弹性碰撞力、顶点与目标曲面的弹性吸引力,及特定顶点的锚固力。这些力可用胡克定律原理进行描述,其公式:
(1)
由胡克定律基本公式可得到网格顶点与顶点相互之间受到的弹力公式:
(2)
在网格形体中,网格的每个顶点都有与之相连接的多个相邻点(Adjacent Vertices),因此在初始时刻所有Edge的平均长度的计算公式:
(3)
顶点受到与之相连的Edge所具有的弹簧力见图6。
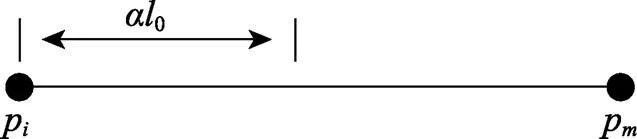
图6 Edge预设目标长度与当前两顶点之间的距离
(4)
两球碰撞时的受力情况见图7。当两球发生碰撞时,计算两球心距离与两倍半径的差值,可得出弹性碰撞力。网格顶点与顶点相互之间受到的弹力:

图7 两球碰撞时的受力情况
(5)
(6)
式(6)中为网格所有顶点的数目。
此外需要对每个顶点设定目标曲面的弹性吸引力,其原理也符合胡克定律:
(7)
(8)
1.3.2 平衡求解
在上述合力的作用下,网格的顶点将在目标曲面上运动。初始状态下网格的顶点位置经过一段时间运动后不再变动(位置坐标不再变化)或小于一定的误差范围(可以自行设置)时,即为平衡状态,其顶点所受的合力为0,该过程变为受力平衡求解问题。Velocity- Verlet[13]算法能较好地模拟整个运动过程,对于此次求解平衡问题其运动过程并不重要,重点是如何快速达到平衡收敛状态。此外还有基于前向欧拉法[14]的简化求解,其特点是将力与点位置直接关联:(无量纲),然后进行迭代更新:。其中为步长;为迭代次数。由于这种方法不要求运动过程的真实性,所以可以快速完成迭代求解,从而满足平衡求解问题的需要。此次基于Kangaroo算法提供的运动求解器(Solver)类似前向欧拉法的迭代求解,可以很方便地进行求解,将以上这些约束力输入求解器,可以设置每次迭代的时间步长(步长越大,运算越快,步长越小,运动过程模拟越真实)。当迭代达到平衡状态时在大多数情况下只需数十秒,即可得到平衡状态下的网格形态。
以优化Delaunay三角剖分网格的内部顶点分布为测试对象,在规定的平面区域内分别生成4种不同数量的随机点(Random Point 2D),并分别进行Delaunay三角剖分形成4种网格。需要在不改变外边框和顶点连线关系的前提下,使网格内部的顶点分布尽可能均匀。使用弹簧力和锚固力作为合力约束,Solve使用默认设置(步长为10)。不同网格面数量的网格计算所用时间的比较见图8。从图8中可以看出,当初始网格面数超过3万时,21 s即可完成求解。当初始网格面数少于1万时,几秒就能完成求解。同时在求解过程中设计师还能实时交互地改变调参系数,直至满意为止。

图8 不同网格面数量的网格计算所用时间的比较
2 具体方法
重拓扑工作流程(见图9)大致可分为3步:绘制低阶(网格面数较少,拓扑关系明确)基本网格;将低阶网格细分并施加动力学找形算法,使之拟合到目标多重曲面上;根据后续工艺需求,设定新网格的面数、边数。在此过程中,对开放多重曲面、闭合多重曲面的操作略有不同,在下文中会有具体阐释。

图9 重拓扑工作流程
2.1 对封闭的多重曲面的重拓扑工艺及纹理制作
由于封闭曲面形体没有边界,所以无法通过边缘作为网格划分的基础。基于网格映射,将多面体或其衍生形体的拓扑结构,通过施加力学约束条件拟合到目标形体上。具体而言,首先根据目标形体的特征选择对应的基础网格形体,并将目标形体包裹。然后通过具体要求进行网格细分,并将网格拟合到目标形体上,完成网格重建,最后便可对网格进行纹理制作等操作。此次需要施加的力学约束条件有每根线段的弹簧力约束;顶点与目标曲面的弹性吸引力;网格所有顶点的球体弹性碰撞力。封闭多重曲面形体的重拓扑过程见图10。
对封闭形体进行网格划分,该方法能很好地控制拓扑结构,包括奇异点的数量和位置,同时网格的变化十分均匀,单元网格的形状质量很高。几何纹理映射制作过程见图11,笔者通过基于网格纹理映射的
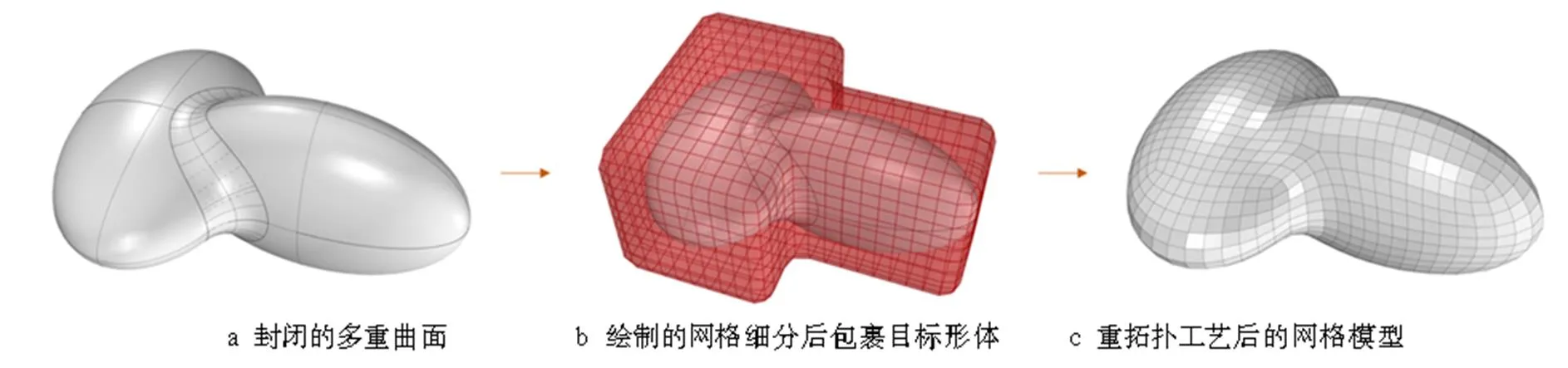
图10 封闭多重曲面形体的重拓扑过程
方法[15]将几何纹理单元(Geometric Texture Units)映射到被优化后的网格表面上,完成了此模型的纹理制作(见图12a)。之后使用光敏树脂,进行SLA光固化立体成型3D打印,见图12b。如果不借助重拓扑工艺下的参数化设计,模具厂的建模能力将无法达到图中所示的效果。

图11 几何纹理映射制作过程

图12 几何纹理生成结果
2.2 对开放的多重曲面的重拓扑工艺及纹理制作
工业生产中大多数的形体都为开放的多重曲面,因此对其进行网格划分具有重要价值。多重曲面所表示的形体类型十分丰富,在此根据形体的具体特点确定使用网格划分方法。
2.2.1 类球面的形体
类球面的形体在空间坐标中的三个维度上其数值都有较大的变化,如果将其投影为平面图形进行网格划分,会出现较大的形状变形,因此更适合使用封闭形体的网格划分方法。需要注意的是在目标形体的开放缺口处,其对应的网格也需要剔除。在施加力学约束条件时,需要将网格开口处的顶点固定到目标形体所对应的边缘上,同时对网格连接线施加弹簧力,并对网格顶点施加体积碰撞力,最后通过网格顶点吸引力将基础网格吸附到目标多重曲面上。开放的类球面多重曲面形体的重拓扑过程见图13。此后,笔者将设计的几何纹理单元嵌入到以重拓扑网格生成的Twisted box中,形成了非常复杂的形态见图14。
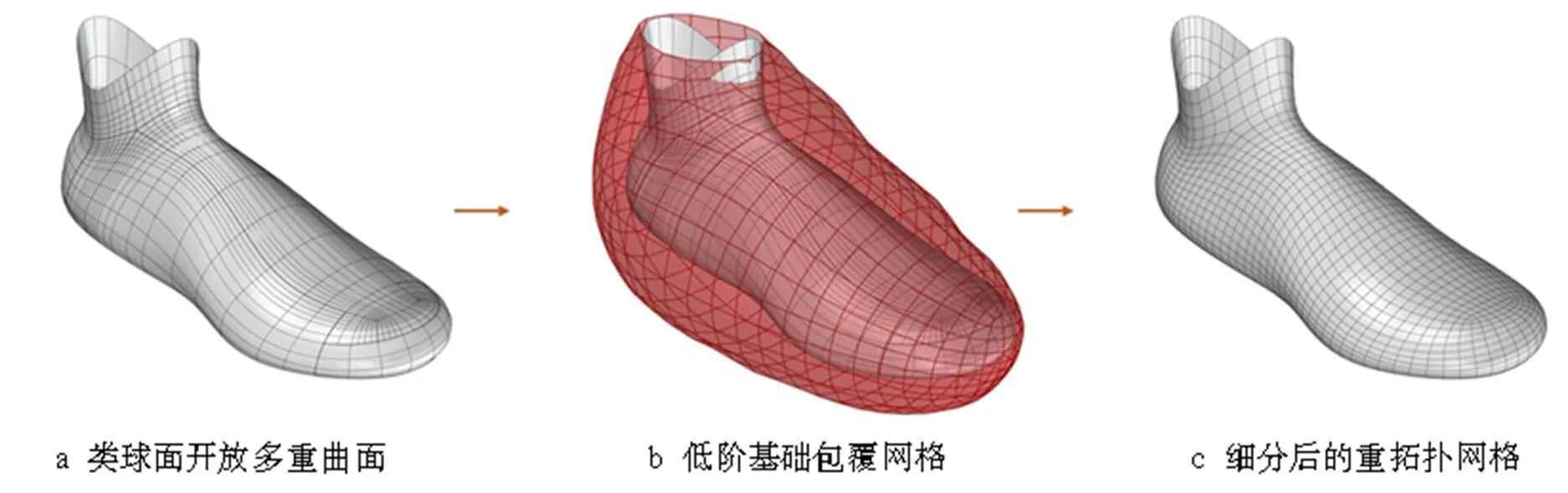
图13 开放的类球面多重曲面形体的重拓扑过程

图14 复杂鞋型的几何纹理生成结果
2.2.2 类平面的形体
当目标形体在空间坐标中只在2个维度有较大的数值变化时,变化维度较小的形变可被忽略,并可以根据形体的平面投影轮廓来重建网格拓扑结构,然后施加力学约束条件将网格拟合到目标形体上。开放的类平面多重曲面形体的重拓扑过程见图15,即为重拓扑过程和纹理制作的流程:将目标曲面的边缘提取出来,并向变化维度较小的坐标轴压缩;通过平面闭合曲线生成均匀连续的基础网格;将平面基础网格通过动力学找形的方法包覆到目标曲面上。
在对原目标曲面进行重拓扑工艺后,笔者通过三角函数干扰算法对新建网格进行了干扰,形成了类似水波纹的效果,此效果已经远远突破了模具厂的建模能力,同时也不浪费其基础模型,可作为后期参数化设计师进行操作的基础模型,见图16。
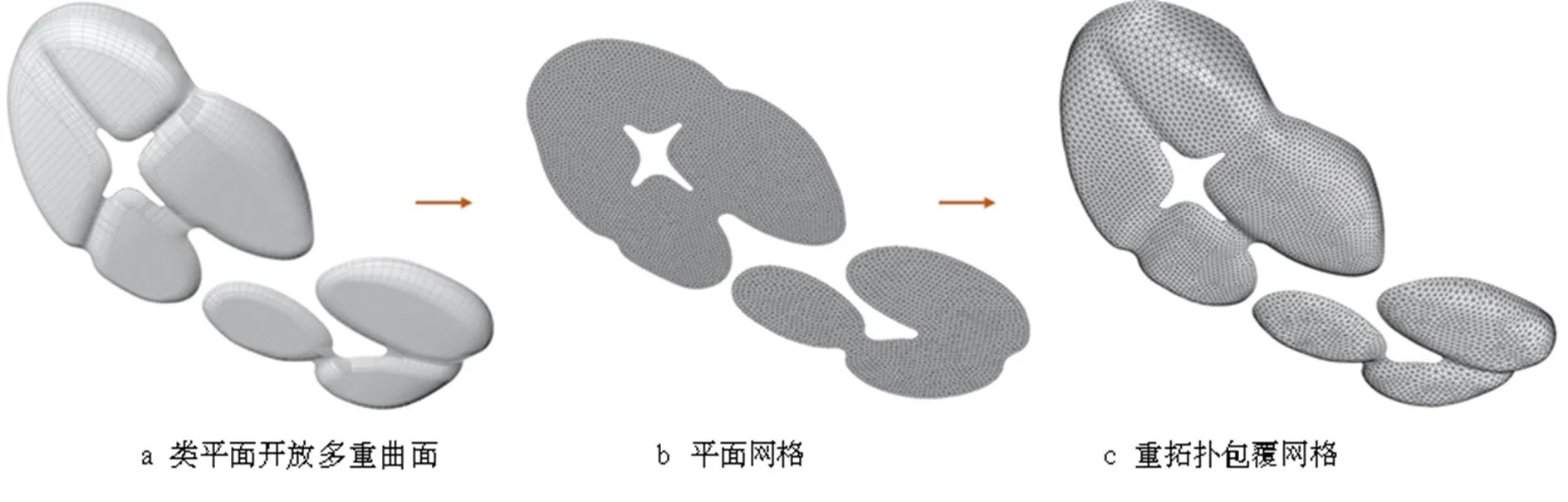
图15 开放的类平面多重曲面形体的重拓扑过程

图16 几何纹理生成结果
3 技术突破及优势
3.1 技术突破:普适性提升
在工业生产领域中,人们常用“边界表示(B-Rep)”法来描述所要加工的物体,此方法是一种根据欧拉拓扑边界构建的几何形状所需的信息,并由计算机保存该信息的方法[16],该方法利于机械设备采用轮廓制造工艺对曲面进行精细化的加工等操作。然而,这种几何描述法的缺点很明显:由于需要对曲面的边缘有清晰定义,在进行面面相接、倒角等操作时,往往出现边界的“非连续”。这种非连续特点,在车辆曲面建模中,往往需要专门的设计师或数模师耗费大量的时间精力进行修复、优化,但在鞋服模具厂的工作中往往被忽略,因为所导致的误差较小,不影响生产。
然而在重拓扑工艺中,几何非连续就会出现很大的问题。Rhino7自带的重拓扑功能见图17。图17a为模具厂提供的曲面文件,通过外露边缘检查(紫色显示)发现很多曲面根本就没有连接上,且无法组合成一个多重曲面(由于设计师建模水平等因素,边缘有空隙)。如果直接对这个模型进行网格重拓扑,计算机就会将整个物件识别成许多的Surface,并逐个分别进行网格化。以Rhino7内置的重拓扑算法为例,输入这样的物件只能达到单一网格内自身的均匀,但整个物件还是无法重拓扑成一个单一网格(如图17b生成出来的结果还是有外露边缘,说明依旧是多个网格)。甚至在一些局部产生破面现象,不能达到全局的网格均匀性。虽然市场上现有的重拓扑工具有很多,如Hypermesh、CreateQuadMesh等,但是想要对上面这样的破面直接进行网格重拓扑也只能生成多个质量良好的单一网格,不过其边缘的连续性无法得到保证,边缘顶点无法一一对应,只能在重拓扑之前手动修补物件不连接的地方,这无疑会增加设计师的负担,减慢开发进度。除了工业领域之外其他重拓扑工具大部分集中在计算机动画软件(如C4D、Maya)或数字雕塑软件(如ZBrush),很难与现有制造业建模水平匹配,而且强行使用这些平台进行重拓扑工作也需要人力进行曲面连续性的优化预处理,同样费时费力。

图17 Rhino7自带的重拓扑功能
针对文中提出的方法,由于基础网格本身就是根据整个物件设计(可以无视曲面不连接的地方,无需对Surface进行修补预处理),再进行动力学找形(网格间增加杆件弹簧力约束其形变不至于过长,同时施加碰撞力使杆件不至于过短),就能保证一次达到均匀网格的效果。此次方法的效果相对传统软件有本质区别,所用平台与模具厂所用的平台一致,均为犀牛(Rhino)平台,非常适用于工业生产、制造领域。工程师只需要重构网格的拓扑关系,即可自动生成设定数目的均匀网格。
3.2 网格自身质量优势
在曲面上进行网格划分无法使每个单元网格完全一致,因此可以在误差允许范围内尽可能地满足特定的需求。一般来说,对于一个优化后的网格,其每个面的形状越“规整”,其形状质量就越好,以三角网格为例,其形状越接近于正三角形,说明其形状质量越高。对于一个网格整体来说,其所有面的面积越近似,说明其整体均匀性越好,这一数据体现在渐变程度方差上。因此,对于一个网格优化算法,形状质量和渐变程度是评价此算法的两大技术指标。
3.2.1 形状质量优势
对于三角网格形状质量的评价,可以通过计算面积与边长之比计算[17]:
(9)
对于四边网格形状质量的评价,可以使用失真系数(distortion coefficient)来描述,其由Lo[18]提出。将四边形依对角线分割成4个三角形,分别计算4个三角形的值并求出一种几何平均值,即通过下面的公式来计算四边网格的形状质量[19]:
(10)
以球面和类球面形体拟合出来的网格为例,在此次评价中用Rhino7内置的QuadRemesh指令作为对比,笔者对目标形体进行重建四边网格,得到网格M_1(此次方法)、M_1(QuadRemesh)和M_2(此次方法)、M_2(QuadRemesh)。形状质量可视化对比见图18,经过以上方法完成的重拓扑网格形状质量好于Rhino7内置的重拓扑指令所生成的网格(红色区域代表网格质量较差,蓝色区域代表网格质量较好)。

图18 形状质量可视化对比
3.2.2 网格渐变程度优势
良好的网格大小渐变能带来一种良好的视觉效果。网格面面积比值见图19。如果每2个相邻网格面面积的比值都相同,也就是说整个网格面是线性变化的,那网格渐变程度也是最均匀的。
由于网格形体的每个面都有其相邻的面,所以可将每个网格面的面积与其相邻网格面的面积之比的平均值作为这个网格面的渐变程度值:
(11)
式(11)中Areai为一个网格面(Face)面积,AdjacentAreaj为Areai相邻的Face面积,n。为相邻面的数量,对于四边网格(除在边缘处的面以外),n=4,γ值越接近1,说明网格变化程度越小。计算每个网格面的γ值,并通过计算其平均值和方差,即可量化比较不同的网格优化方法。
图19 网格面面积比值
Fig.19 Ratio of area for faces
操作过程:采用控制变量法,将此次方法与Rhino7内置的QuadRemesh方法分别重拓扑M_1及M_2形体为四边网格,并分别对比所生成的网格形状质量与渐变程度。表中最重要的指标为形状质量的方差与渐变程度的方差,数值越小说明越优异。
网格质量对比见表1。通过表1的数据可以看出,使用此次方法获得的网格渐变程度,较Rhino7原装方法其方差值有明显变小,这说明在对目标形体的网格重建中,用此次方法获得的视觉效果更均匀,更利于后续工作的开展。同时此次方法在处理奇异点的数量和位置上更具灵活性,其他软件自带的重建网格指令则根本无法控制奇异点的数量和位置。此次方法奇异点的分布(见图20a)相比Rhino7原装方法奇异点的分布(见图20b)更加均匀。对于更加复杂的形体,奇异点的可控制也比其他软件生成得更理想。
表1 网格质量对比

Tab.1 Mesh quality comparison

图20 奇异点分布对比
4 结语
随着计算性设计时代的到来,设计与数据的关系越发紧密。在目前消费品设计领域,计算机多半还是承担“辅助设计”的角色,数据传递的信息主要是设计师对产品几何的描述,并由工厂生产。这样的设计闭环并未将数据在设计端的意义发挥到极致,缺乏数据监测及反馈对产品的优化。设计师依旧是凭借经验在优化现有的产品。同时由于加工厂商的建模能力约束,很多设计师所希望的表皮纹理设计也很难实现,一旦需要连续的肌理,就必然涉及到“跨面操作”。这项操作在建模工程中会遇到不小的阻碍,会拉长设计周期,对商业设计有致命影响。
借助文中提出的“基于动力学找形的重拓扑工艺”方法,模具厂绘制的B-rep模型可以被快速转换为分布均匀、形态规则、面数可控的连续网格。这一方法既没有浪费模具厂对模型准确绘制的基本功,同时也为未来更多的数字设计师提供了模型接口,避免了他们独立处理“非连续多重曲面“时的重复劳动。在产品的优化设计过程中,将基础形体快速转换成以网格表示为基础的数字化模型,可以在前期的设计过程中方便地介入有限元分析,并通过参数化的控制直接修改、调整网格,加快迭代优化过程。此外甚至可以接入用户数据采集作为基础网格形态变化的依据,从而实现形态的快速定制化生成。
模型转换效率看似是一个量变的过程,其实是产品数据链的“润滑剂”,在一个开发周期较紧张的商业项目中,模型文件转换效率的提升可以让研发团队、数字服务团队更快地同时参与到项目中来,从而更高质量地为设计到制造的开发体系奠定基础。
[1] BÖHM W, FARIN G, KAHMANN J. A Survey of Curve and Surface Methods in CAGD[J]. Computer Aided Geometric Design, 1984, 1(1): 1-60.
[2] PIEGL L, TILLER W. The NURBS Book[M]. Springer Science & Business Media, 1996.
[3] HETTINGA G J, KOSINKA J. Conversion of B-rep CAD Models into Globally G1 Triangular Splines[J]. Computer Aided Geometric Design, 2020, 77: 101.
[4] OWEN S J. A Survey of Unstructured Mesh Generation Technology[J]. 7th International Meshing Roundtable, 1998, 239: 267.
[5] FORTUNE S. Voronoi Diagrams and Delaunay Triangulations[M]. Computing in Euclidean geometry, 1995: 225-265.
[6] LI Y, JI S. A Geometric Algorithm Based on the Advancing Front Approach for Sequential Sphere Packing[J]. Granular Matter, 2018, 20(4): 59.
[7] CHOI C P, GU X, LUI L M. Subdivision Connectivity Remeshing Via Teichmüller Extremal map[J]. Inverse Problems & Imaging, 2017, 11(5): 825-855.
[8] 王奇胜, 高博青, 吴慧. 基于引导线偏移的建筑网格生成方法[J]. 上海交通大学学报, 2019, 53(9): 1040-1044.
WANG Qi-sheng, GAO Bo-qing, WU Hui. An Architectural Grid Generation over Free-Form Surfaces Based on Guide Curve Offsetting[J]. Journal of Shanghai Jiao Tong University, 2019, 53(9): 1040-1044.
[9] WEIZMANN M, AMIR O, GROBMAN Y J. Topological Interlocking in Architecture: A New Design Method and Computational Tool for Designing Building Floors[J]. International Journal of Architectural Computing, 2017, 15(2): 107-118.
[10] GAO B, LI T, MA T, et al. A Practical Grid Generation Procedure for the Design of Free-form Structures[J]. Computers & Structures, 2018, 196: 292-310.
[11] MIZOBUTI V, JUNIOR L C M V. Bioinspired Architectural Design Based on Structural Topology Optimization[J]. Frontiers of Architectural Research, 2020, 9(2): 264-276.
[12] PIACENTINO G. Weaverbird: Topological Mesh Editing for Architects[J]. Architectural Design, 2013, 83(2): 140-141.
[13] MARTYS N S, MOUNTAIN R D. Velocity Verlet Algorithm for Dissipative Particle Dynamics Based Models of Suspensions[J]. Physical Review E, 1999, 59(3): 3733.
[14] PERSSON P O, STRANG G. A Simple Mesh Generator in Matlab[J]. Siam Review, 2004, 46(2): 2004.
[15] HECKBERT P S. Survey of Texture Mapping[J]. IEEE Computer Graphics and Applications, 1986, 6(11): 56-67.
[16] HIEMSTRA R R, SHEPHERD K M, JOHNSON M J, etal. Towards Untrimmed Nurbs: CAD Embedded Reparameterization of Trimmed B-rep Geometry Using Frame- field Guided Global Parameterization[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 369: 113.
[17] FIELD D A. Qualitative Measures for Initial Meshes[J]. International Journal for Numerical Methods in Engineering, 2000, 47(4): 887-906.
[18] LO S H. Generating Quadrilateral Elements on Plane and over Curved Surfaces[J]. Computers & Structures, 1989, 31(3): 421-426.
[19] PARK C, NOH J S, JANG I S, et al. A New Automated Scheme of Quadrilateral Mesh Generation for Randomly Distributed Line Constraints[J]. Computer-Aided Design, 2007, 39(4): 258-267.
Discontinuous B-rep Geometry Topology Reconstruction in Dynamic Form-finding Method
YUAN Chao, ZHANG Xiao, QIU Song
(Tsinghua University, Beijing 100084, China)
This paper aims toconvert files of the Boundary Representation (B-rep)model in industrial modeling engineering to files of the Uniform continuous mesh model efficiently through retopology, which provides a bridge for parametric design and finite element analysis, further construct a closed loop of parametric design workflow.Through algorithm plug-in based on Rhino platform, the basic mesh preset many constraints such as the spring force of the rod, the anchoring force of the boundary and the attractive force of the target is wrapped onto known B-rep shapes. And through dynamic multiple iteration algorithms, the retopology mesh is infinitely approached to the original surface. Finally, the basic mesh is reconstructed into a uniformly continuous four-sided mesh with a controllable number.After this process, the designer only needs to do a few clicks operation, and the discontinuous B-rep shaper can be re-topological within a few minutes. The new mesh obtained is uniform and continuous, and the number of faces is controllable, saving a lot of manpower repair time.By providing retopology method based on dynamic algorithm, parametric designer can Connect factories more smoothly, and finite element analysis will be more efficient to aided support design. It is one of the important technical foundations of industrial design digital closed loop.
dynamic form-finding; retopology; parametric design; mesh mapping; finite element analysis; data closed loop
TB472
A
1001-3563(2022)10-0158-11
10.19554/j.cnki.1001-3563.2022.10.019
2022-01-02
袁潮(1996—),男,硕士生,主攻工业设计。
邱松(1964—),男,硕士,教授,博士生导师,主要研究方向为设计形态学。
责任编辑:马梦遥

