5G环境下配网差动保护采样数据缺失应对策略
涂崎, 沈冰, 邹晓峰, 金震, 徐舒, 侯炜
(1. 国网上海市电力公司,上海 200122;2. 国网上海市电力公司电力科学研究院,上海 200437;3. 南京南瑞继保工程技术有限公司,江苏 南京 211102)
0 引言
近年来,分布式电源(distributed generation, DG)大量接入,导致配电网由传统单端辐射式结构转变为多端多电源结构,形成了有源配电网[1—2]。有源配电网的运行方式、线路潮流与传统配电网之间均存在较大差别[3—5],潮流双向性及DG故障时馈出电流的新特征,对有源配电网保护提出了更艰巨的挑战,传统配电网中应用广泛的三段式过流保护已难以满足有源配电网的正常运行要求[6—8]。基于双端信息量的电流差动保护在具备光纤信道条件下能充分解决上述问题,提升有源配电网的保护水平,但由于敷设光纤成本高、运维困难等原因,目前仅被部分发达地区及新能源场站接入线采用。
5G作为新一代移动通信的领跑者,具有高可靠性、低时延等满足差动保护通信要求的优势[9—10],已有不少学者将其引入配电网差动保护领域[11—12],但无线环境下5G可能受噪声干扰导致传输数据缺失[13]。而现有的差动保护方案中,若采样点缺失数超过一定数量,应将主保护闭锁[14],故障隔离完全依赖后备保护。采样数据缺失场景下,为继续发挥差动主保护的作用,现常用手段是利用插值拟合法重构缺失的采样点参与保护计算。文献[15]提出一种线性Lagrange插值算法,计算量较小且在测量波形含低次谐波时能满足最基本的精度要求;文献[16]提出一种二次插值算法,能在不提高保护装置采样率的前提下,基本消除差动保护动作模糊区的影响;文献[17]提出一种三次样条插值算法,在测量波形含高次谐波时插值精度有一定的优势。但现有算法很难兼顾计算量与插值精度,亟须探究一种合适的算法以解决差动保护采样数据缺失问题。
三段式过流保护难以适配有源配电网日益增长的保护水平需求,基于5G通信的差动保护有望解决该问题。但5G通信可能受外部干扰导致采样数据缺失,对保护的正确动作造成一定影响,而现有的插值应对手段难以兼顾计算量与插值精度。为解决上述问题,文中提出一种5G通信环境下有源配电网电流差动保护采样数据缺失应对策略,在插值精度方面有一定优势,且能在保护尽量不误动的前提下提升耐受的缺失点数量,不会影响保护实时性。
1 5G通信环境下有源配电网线路差动保护配置方案
5G三大应用场景:增强型移动带宽(enhanced mobile broadband,eMBB)、高可靠低时延通信(ultra-reliable and low latency communications,uRLLC)、大规模机器类通信(massive machine type communications,mMTC)[9],其中以uRLLC场景与有源配电网差动保护通信需求最为吻合。在差动保护uRLLC场景下,5G通过移动边缘计算(mobile edge computing,MEC)降低通信时延,通过多连接技术大幅提升通信可靠性,理论性能指标能够满足差动保护的基本要求。
图1为5G差动保护在某线路BC上的配置方案,目前国网和南网在青岛、深圳、成都等地所建设运行的示范工程中基本都采用了该方案。在外部时钟源信号下,线路两侧通过对时装置完成数据通信同步。完成通信同步后,两侧保护装置收集本侧电流互感器(current transformer,CT)采集的电流采样信息,通过无线客户前置设备(customer pre ̄mise equipment,CPE)、5G基站和5G核心网发送到对侧CPE终端,对侧保护装置根据两侧电流采样信息进行保护判别,若判别结果为区内故障则跳开线路两侧断路器,否则保护不动作。
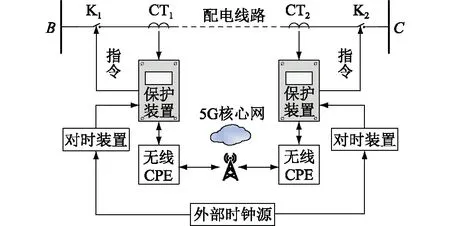
图1 5G在线路BC上的配置方案Fig.1 5G configuration scheme on line BC
但就目前的5G网络而言,仍存在传输时延抖动大、丢包率较高等主要问题。已有学者研究指出:5G通道的丢包率约为10-5,较光纤通道10-9的丢包率提升了约10 000倍[18],所以5G通道比光纤通道丢帧的概率更大。丢包问题在光纤差动保护中就已引起广泛关注,通常采用对缺失的采样点作插值的方式解决,5G通信环境下差动保护若发生采样点缺失问题或可沿用该方式解决[19]。
2 采样点缺失对有源配电网差动保护影响
有源配电网模型如图2所示,C母线上有逆变型分布式电源(inverter interfaced distributed generation,IIDG)并网。

图2 有源配电网模型Fig.2 Active distribution network model
为充分体现有源配电网差动保护有别于三段式保护的作用,对于含IIDG的配电网,一般应在IIDG并网点上下游相邻线路上配置差动保护,如图1中BC及CD线路。为方便分析,设C侧CPE发送数据受瞬时干扰导致少数采样数据缺失,下文通过ρ平面法[20—22]分析该场景对BC线路保护性能的影响。
2.1 差动保护ρ平面分析法
ρ平面法在差动保护分析中应用广泛,能在复平面中直观地反映运行状态点,且能划分动作区和制动区。前文已设采样数据缺失仅发生于C侧,因此B侧电流幅值将比C侧大,ρ平面法以B侧电流为基准进行分析。相量和差制动判据为:
(1)
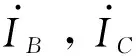

(2)

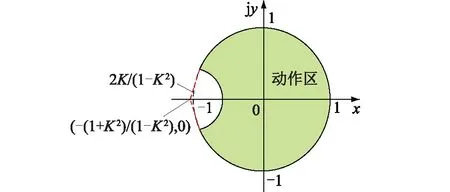
图3 差动保护ρ平面判据Fig.3 Differential protection ρ plane criterion
2.2 不同场景下采样数据缺失对差动保护的影响
图2中,若BC线路发生区内短路故障,则IIDG和系统电源馈流能力存在显著差距,故障后线路两侧差流很大[23],此时5G通信干扰所致采样数据缺失对保护判别影响可忽略不计,保护依然能根据大差流正确判别。但BC线路正常运行和发生外部故障时,采样数据缺失可能导致保护误动,为此,下文将以BC线路发生区外三相短路故障为例,深入分析采样数据缺失对保护动作性能的影响。
设保护装置采样频率fs=1 000 Hz,周波采样点数N=20。采样数据进入保护算法前一般都要经过差分滤波消除衰减直流分量[17],为便于说明,对算例中BC线路发生区外三相短路故障后C侧电流在滤除直流分量后的采样周波数据点进行编号,如图4所示。
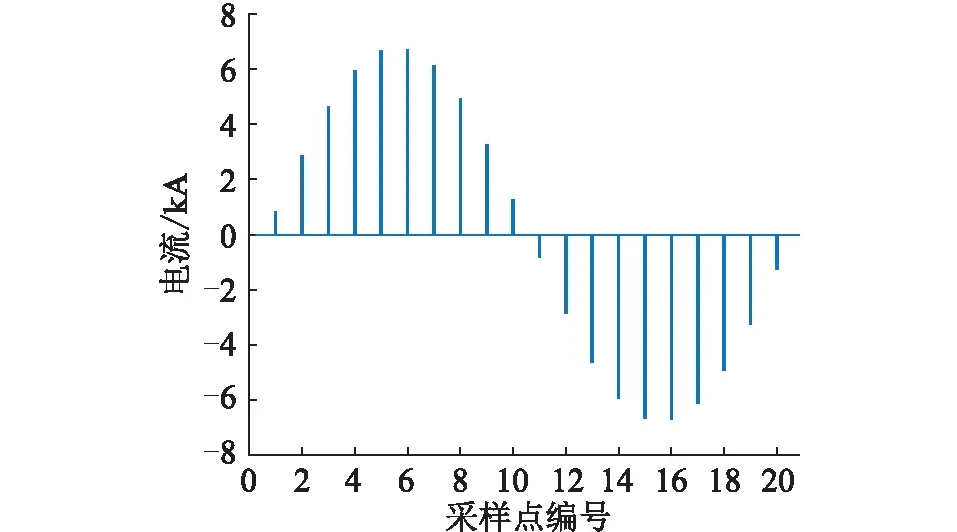
图4 故障后周波采样电流Fig.4 Cyclic sampling current after fault
一般而言,采样点缺失场景有缺失点数量、缺失连续性、缺失位置3种决定性特征,而5G干扰的随机性势必导致同一场景下的3种特征存在重合区。利用控制变量法,在3种特征下的不同采样数据缺失场景中,用ρ平面法表示出各种场景对应的保护状态点,通过分析状态点的位置定性研究采样点缺失对保护的影响。
2.2.1 采样点缺失数量对保护的影响
控制采样数据缺失的起点相同,从第3点开始连续增加缺失点数量,给出包括采样点未缺失在内的6种场景下(状态点分别为a1:未缺失;b1:点3缺失;c1:点3,4缺失;d1:点3,4,5缺失;e1:点3,4,5,6缺失;f1:点3,4,5,6,7缺失)保护的动作情况,如图5所示。

图5 采样点缺失数量对保护的影响Fig.5 Impact of missing number of sampling points on protection
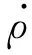
2.2.2 采样点缺失连续性对保护的影响
采样点缺失连续性问题有连续缺失、等间隔缺失、间隔式连续缺失、无规则缺失4种特征。缺失点数量为4时已可基本涵盖以上4种特征,下文控制缺失点数量和缺失起点相同,通过6种缺失场景 (状态点分别为a2:点2,3,4,5连续缺失;b2:点2,3,5,6间隔式连续缺失;c2: 点2,4,6,8等间隔缺失;d2:点2,3,5,7无规则缺失;e2:点2,4,5,7无规则缺失;f2:点2,4,7,9无规则缺失),结合图6所示的保护动作情况,分析采样点缺失连续性对保护的影响。
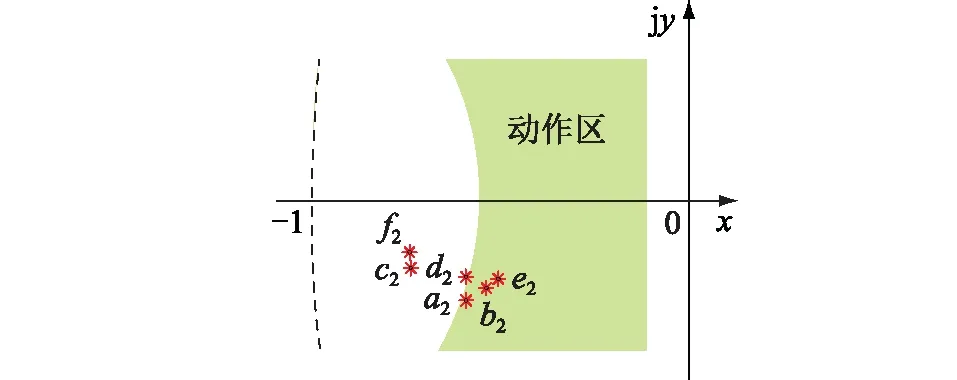
图6 采样点缺失连续性对保护的影响Fig.6 Impact of missing continuity of sampling points on protection
在图6所示的ρ平面(缩放)中,只有采样点连续缺失场景下的状态点a2的相位偏离图5中未缺失场景下的状态点a1相位最远。但在分析采样点缺失连续性问题时,不同的缺失连续性场景必然伴随缺失点位置的不同,所以才导致图6中保护的动作情况呈现出极大的不确定性。若仅作定性分析,可得结论:在各种采样点缺失连续性场景中,连续缺失对保护动作的影响更大。
2.2.3 采样点缺失位置对保护的影响
控制采样点缺失数量和缺失连续性相同,以采样点连续缺失3点为例,通过6种缺失场景(状态点分别为a3:点2,3,4缺失;b3:点3,4,5缺失;c3:点4,5,6缺失;d3:点5,6,7缺失;e3:点6,7,8缺失;f3:点7,8,9缺失),结合图7所示的动作保护情况,分析采样点缺失位置对保护的影响。

图7 采样点缺失位置对保护的影响Fig.7 Impact of sampling points missing location on protection
在图7所示的ρ平面(缩放)中,缺失场景的状态点从a3~f3,从图4中可以看出3个缺失采样点的位置正好穿越了一个波峰,而保护的动作情况为不动作—动作—不动作。结合傅式算法分析认为,在峰值位置发生采样数据缺失时,计算得到的C侧电流相量幅值在上述场景中下降得最为严重。分析可得结论:波形峰值附近发生采样点缺失最容易导致保护误动。
3 基于Neville插值的采样数据缺失应对策略
通过第2章的分析发现,5G环境下采样数据缺失对保护的影响不容忽视。为在有源配电网中更充分地利用差动保护这一性能优越的保护原理,可通过采用适当的插值算法对缺失采样点进行插值重构,替代其参与保护计算,一定程度上能弥补提升保护的动作性能。为此,文中提出一种阶次组合Neville插值法,能够在提升计算精度的同时降低缺失采样数据对保护动作的影响。
3.1 Neville插值算法
Neville是一种线性迭代的插值算法,在测绘科学领域的GPS精密星历中应用比较成熟[24—27],但在电力领域中尚未引起广泛关注,有望解决采样点缺失问题。
其基本思想为:插值区间内,将若干个低阶插值式两两组合成高一阶的插值式,再将这些高一阶的插值式两两组合成更高一阶的插值式。通过不断组合迭代,插值式逐渐向更高阶发展,直至该插值式刚好通过所有已知数据点,此时可用此插值式进行任意缺失时刻的插值。
采用Neville进行插值的具体步骤为:对于n+1个基本数据点序列(xk,yk),k=1,2,…,n+1,必有n次插值多项式通过所有基本点。假设I(i,w)为w-i次插值多项式(1≤i≤w≤n+1),且I(i,w)通过点(xm,ym),m=i,i+1,…,w。Neville插值法首先确定了n+1个只通过一点的最低次“零阶多项式”,即:当i=w时,I(i,w)=I(i,i)=yi。
其次利用这些“零阶多项式”两两组合成通过2点的“一阶多项式”,后续步骤即将前一步所得低阶式不断组合直到最高阶多项式的过程。
当w-i≥1时,I(i,w)满足如下迭代关系:
(3)
式中:x0为待插值点横坐标。
因此,若已知图4中全周期N=20个基本数据点(x1,y1),(x2,y2),…,(x20,y20),假设仅在第5个点发生了数据缺失,欲在位置x5处进行插值,则进行如下操作。
步骤1:
(4)
步骤2:
(5)
依次类推。
步骤19:
(6)
式(6)计算所得即为第5个数据点的插值结果。同理,在发生多点数据缺失时,也可按照上述步骤进行插值,相应的计算步骤会进一步减少。
3.2 阶次组合法
采用Neville法进行高次插值拟合时经常出现龙格现象,具体表现为:插值区间边缘存在严重误差,插值曲线边缘有大幅度振荡,且插值阶数越高,误差和振荡幅度越大。针对上述问题,为提升插值精度,提出一种阶次组合法的应对措施,基本处理方式是:在插值区间中部使用高次插值,插值区间边缘使用低次插值,通过这种高次与低次插值相组合的阶次组合方法消除龙格现象。
阶次组合原理:对p个基本点序列(x1,y1),(x2,y2),…,(xp,yp),区间各处插值结果yx应满足下式:
(7)
式中:Ih1,Ih2分别为利用首、末端h个基本点的低阶插值式;Ip为利用全p个基本点的高阶插值式。xs表示从基本点x1~xs均应适用低次插值函数Ih1(x),满足条件xs<(x1+xp)/2,xp+1-s可类推。
为消除Ih1,Ih2边缘点插值的龙格现象,h不宜太大,而为了防止低次插值时缺失点过多导致无法插值,h选取不宜太小。因此,对于全周N=20个采样点,若缺失点数量达到半周N/2=10,考虑到至少3点才有较好的插值效果,应选取h≥13。
综上,文中阶次组合方式拟选取为:在整周期N=20个采样点中,前(后)8个点区间使用基于前(后)13个点的低阶Neville插值,中部4个点区间使用基于整周期20个点的高阶Neville插值。
3.3 5G环境下有源配电网差动保护采样数据缺失应对策略
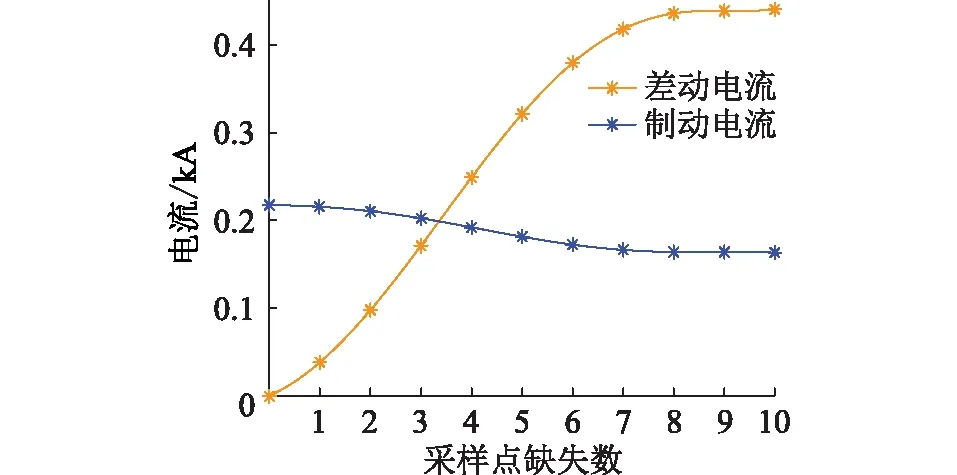
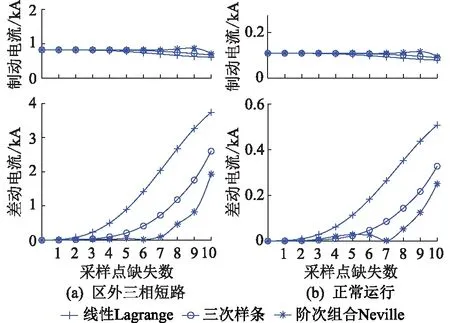
为更有效地应对5G环境下有源配电网差动保护采样数据缺失问题,可利用上述阶次组合方法进行数据插值:保护启动后收集对侧整周期采样数据并判断其中缺失点数量Ns,Ns≥Nm时将差动主保护闭锁并启动后备保护;Ns 图8 差动保护采样数据缺失应对策略Fig.8 Countermeasures for sampling data missing of differential protection Nm整定原则及方式为:尽管当前已有较成熟的数字滤波器,在数据进入相量算法之前能够滤除短路电流中的非周期分量,但仍可能存在一定的谐波残留,因此引入可靠系数Krel。借鉴传统保护考虑互感器测量误差、计算误差、非周期分量影响等因素后,Krel的选取一般在1.1~1.5。为了可靠起见,文中选取Krel=1.5。引入可靠系数后,通过仿真得到使用文中方法后须在采样点缺失数量为8时将差动主保护闭锁,即引入可靠系数后,Nm=8。 为验证所提应对策略的有效性,在PSCAD中搭建了图2所示有源配电网模型。参数设置为:线路单位阻抗均为0.193 5+j0.561 1 Ω/km;线路长度AE为4 km,EF为4 km,AB为2 km,BC为4 km,CD为3 km,AG为2 km;负荷均为1.0+j0.2 MV·A。IIDG采用PQ控制方式,正常运行时有功功率为1 MW,无功功率为0。需先说明的是,后文多种插值法均属于内插法,因此不考虑区间端点缺失。 由前文可知,采样点连续缺失对保护影响最大,深入分析该场景,通过增加缺失点数量对比3种插值法,即线性Lagrange、三次样条(自然边界条件)、阶次组合Neville的性能。仿真从第2点开始逐渐增加缺失点数量(上限为N/2=10),图9为使用3种插值法的幅值与相位误差。 从图9可看出,缺失点数量增加时3种插值法的幅值与相位误差均显著增大,其中线性Lagrange插值法的误差增幅最明显,其次是三次样条插值法,而阶次组合Neville插值法误差最小。 图9 缺失点数增加时3种插值法的误差Fig.9 Errors of the three interpolation algorithms when missing number increases 为验证所提阶次组合Neville插值法提升保护动作特性的有效性,文中将深入分析采样数据连续缺失场景下,发生区外三相短路故障与正常运行时使用插值法与不使用插值法的效果对比。需先说明的是,下文只进行了线路单侧发生采样数据缺失场景的分析,但在极端场景下两侧数据同时缺失也可得出相同的结论,文中限于篇幅不详证。 4.2.1 不使用插值法时保护的动作特性 图10 缺失点数量增加时差动电流和制动电流的变化趋势(不使用插值法)Fig.10 Variation trend of differential current and braking current with increasing number of missing points (without interpolation method) 4.2.2 3种插值法提升保护动作特性的效果对比 图11 缺失点数量增加时差动电流与制动电流的变化趋势(使用3种插值法)Fig.11 Variation trend of differential current and braking current with the increase of the number of missing points (using three interpolation methods) 从图11中可看出:缺失点数量增多至超过8个点时,3种插值法都因误差过大导致差动电流大于制动电流,此时仅依靠插值难以保证保护正确动作,应启用后备保护。同时在3种插值法中,阶次组合Neville插值法使保护在采样点缺失数为8时正确动作,能耐受的缺失点数量多于另2种插值法。 前文仿真中均使用图4所示数据窗,而实际保护装置中数据窗是移动的,需要验证移动数据窗下所提方法的有效性。限于篇幅,以第2到第10点缺失为例,最开始该缺失数据段位于插值法所用全周数据最末端,随着采样进行,该数据缺失段在插值法所用全周数据的位置将逐步前移,直至位于首段位置。针对上述数据窗移动过程,再次进行上述仿真,结果如图12所示,可以看出在移动的数据窗下,以保护不误动为前提,阶次组合Neville插值法能耐受缺失点数量仍多于另2种插值法,性能更优越。 图12 缺失点数量增加时判据差动电流与制动电流的变化趋势(移动数据窗)Fig.12 Variation trend of the criterion differential currentand braking current with the increase of the number of missing points (under the moving data window) 根据3.1节中Neville插值法的描述,若有n+1个数据点,从步骤2开始将出现加法和乘法计算,考虑到重复数据不用计算,步骤2中的加法计算为n次xr-xr-1(2≤r≤n+1)、n+1次x0-xt(1≤t≤n+1)以及n次分式和,即共有3n+1次加法计算;步骤2中由于每个式子的分母相同,共有3n次乘法计算。同理可分析其他步骤中加法计算和乘法计算的计算量,最终求得n+1个数据点进行Neville插值需要n2+3n+1次加法计算和3n(n+1)/2次乘法计算。 为展开对比,应对当前常用的三次样条插值法进行计算量分析,其一般采用追赶法[28]求解三对角矩阵。在“追”的过程中,共有3(n-1)次加法和6n次乘法计算;在“赶”的过程中,共有n-1次加法运算与n次乘法计算。求解三对角矩阵后,对样条参数进行求解,需要5(n+1)次加法计算和6(n+1)次乘法计算。因此,在三次样条插值过程中,共须进行9n+1次加法计算和13n+6次乘法计算。 但是,使用阶次组合Neville插值法(n=20),周期前(后)8个点是基于13个点的插值,需要181次加法和234次乘法。而三次样条插值法是基于整周期20个点的插值,需要172次加法和253次乘法。与三次样条插值法相比,阶次组合Neville插值法多9次加法、少19次乘法。对于目前高速发展的中央处理器性能,其加法和乘法所需时间均极短,传统三次样条法适用的场合,文中所提方法与之计算量相差无几,不会对保护速动性造成明显影响。 文中研究5G环境下有源配电网差动保护采样数据缺失场景,得到以下结论:(1) 提出一种在缺失点数量未达到整定阈值时使用阶次组合Neville插值法进行数据插值、缺失点数量超过整定阈值时闭锁主保护的应对策略;(2) 对比传统方法,所提阶次组合Neville插值法性能相对较好,能耐受的缺失点数量更多;(3) 所提阶次组合Neville插值法不会给保护速动性带来较大影响。综上,当有源配电网差动保护与5G通信紧密结合时,文中所提应对策略有望得到广泛应用。 本文得到国网上海市电力公司科技项目(52 ̄0 ̄9 ̄4 ̄0 ̄1 ̄9 ̄0 ̄0 ̄6B)资助,谨此致谢!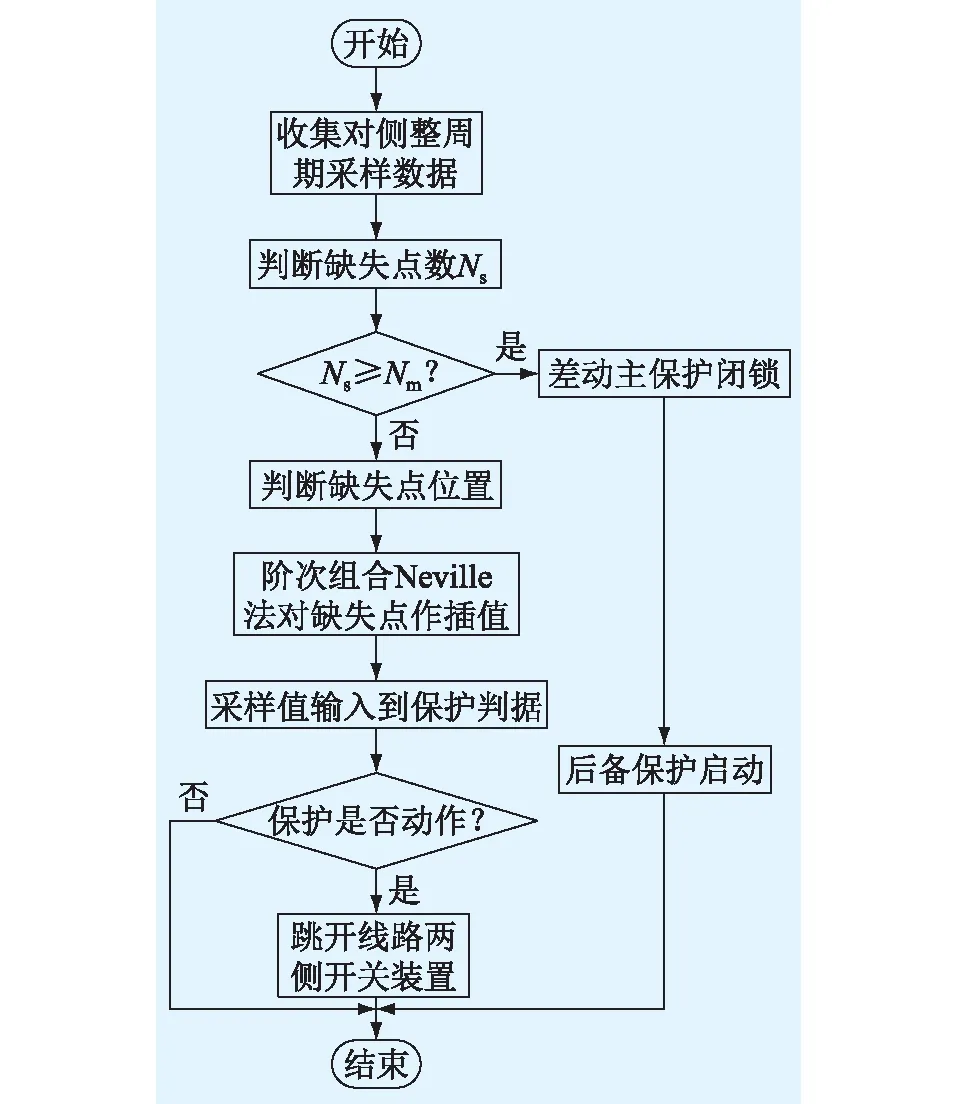
4 插值性能及对保护速动性影响仿真验证
4.1 多种插值法的性能比较
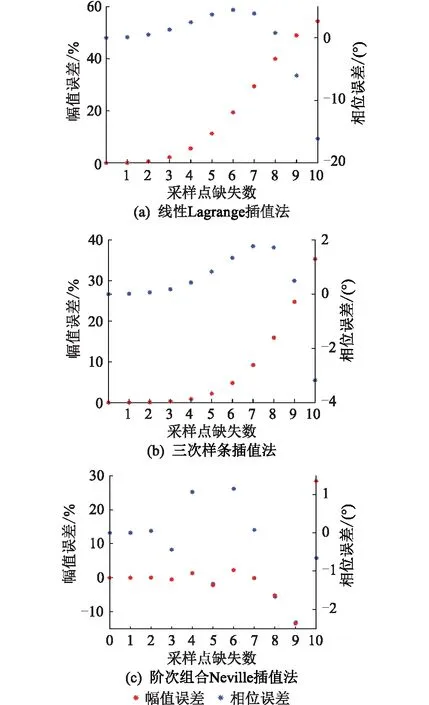
4.2 多种插值法提升保护动作特性的效果对比



4.3 阶次组合Neville插值法对保护速动性的影响
5 结论

