电气传动设备低频-前馈复合控制技术

王 浩

(国网江苏综合能源服务有限公司，江苏 南京 210019)

0 引言

各个行业都离不开电气能源供给。目前，综合能源已作为主流能源接入电气传动设备，推动电气设备的运转和所需能量转换。但能源接入对电气传动设备造成能量冲击的同时，也会产生相应的干扰，不利于生产工作效率，也对周边居民的生活环境产生影响，因此对综合能源接入下电气传动设备低频-前馈复合控制的研究迫在眉睫。

传统控制方法更多关注高频扰动的去除，侧面加重了设备自身的承载负担，还会影响电气传动设备的散热，且扰动抑制效果并不理想，传动设备的高频扰动无法消除。为此，冯硕[1]优化包装机电气控制系统，从伺服系统机械传动方面减少高频扰动现象。徐大可等[2]建立了具有惯性响应和一次调频能力的虚拟同步发电机控制策略，快速调整有功功率的合理分配与荷电状态，减少外界干扰。

综合以往研究方法，提出一种综合能源接入下的电气传动设备低频-前馈复合控制技术。

1 电气传动设备扰动信号采集和预处理

在电气传动设备上安装信号采集传感器[3]，对电气设备产生的干扰进行采集，将采集的扰动信号作为初级信号，利用扬声器还原采集好的初级扰动信号，用S0表示，利用预处理控制初级扰动信号，得到控制后的扰动信号S1，对比二者信号间的误差，统计形成误差变量函数，即

(1)

e1(t)为时间为t1时传感器的误差信号；N为安装前馈装置的任意一点。为了估计出不同位置的控制性能[4]，将误差变量归一化处理，用标准函数表示为

(2)

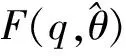
2 电气传动设备有限分析元模型

为了更好地控制综合能源接入电气传动设备所产生的扰动现象[6]，建立电气传动设备有限分析元模型。在传动作业时，电气设备表面振动频幅是影响扰动信号大小的主要因素，本文采用边界元法对其求解，分析电气传动设备表面结构，在表面结构分析元网格上，完成电气设备外部声场的计算。

电气传动设备表面振动下，其自身所辐射出来的声压用p(r,t)表示，在满足电气设备外部声场的声学边界条件下，引入声学函数：

Δ2p(r,t)-k2p(r,t)=0

(3)

(4)

(5)

Δ2为拉普拉斯算子；r为电气设备表面立体声场中Q、P这2点间的物理距离，Q为电气传动设备表面S上的任意一点，P为电气传动设备底部范围任意一点；k=wlc为扰动波数，w为声音振动频率，c为扰动信号在空气中传播声速；n为单位矢量；a(r,t)为电气传动设备表面垂直方向振动加速度；rs为电气传动设备振动表面上任意一点。谐波电压Un的有效值表达式为

(6)

对其求解，可得

(7)

将谐波电压的求解结果与式(3)～式(5)联立，进一步推导，获取电气传动设备的底部外场声压p(P)与垂直方向振动加速度a(r,t)，设置设备外场扰动情况的微分方程式，即

c(P)p(P)=

(8)

c(P)=α/4π，α为电气传动设备表面结构上P点的表面呈现角度；a(Q)为电气传动设备三维声场中Q点处垂直方向振动加速度；S(Q)为包含Q点在内的电气设备表面面积。

利用边界元法将式(6)中各个单元及节点离散处理，得到结果为

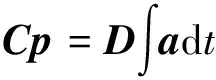
(9)

C、D为描述干扰对电气设备所产生的影响矩阵[7]；p为电气传动设备作业时在分析元网格各节点上的声压向量[8]；a为电气设备网格上各节点在垂直方向的加速度向量。利用插值法，对式(9)求解，得到电气传动设备底部空间上外场中任意一点P处的作业辐射声压p(P)，即

(10)

c、d为电气设备运行时所产生干扰的差值系数矩阵。

3 电气传动设备低频-前馈复合控制技术

3.1 物理隔声控制

在电气传动设备上，附加物理隔声装置[9]，在进行传动作业时，电气传动设备自身所产生的电压位于设备顶部和底部，形成上下环绕的电场力，中间部位虽属于电场力中，但处于相对平衡状态，将隔声腔安装在电场力相对稳定的部位，能够更好地控制扰动信号传播，不会影响电器传动设备的正常作业。因此，本文将物理隔声腔安装在电气传动设备的中间部分，通过简化电气传动设备，可以得出其周围两极电场力和激励电压之间的关系[10]。

两极板之间的电场力为

(11)

A为极板面积；ki为电极之间的距离；u(t)为电压。

附加隔声腔后，电气传动设备的基波电压为

u0(t)=U0sinwt

(12)

U0为电气传动设备的基波电压有效值；w为角频率。

谐波电压表示为

un(t)=Unsinwt

(13)

Un为电气传动设备的谐波电压有效值。

附加隔声腔的电气传动设备上，基波和各个谐波叠加后的电压表示为

u(t)=u0(t)+un(t)

(14)

联立以上公式，可以得到电气传动设备的电场力为

(15)

其中，基波电压的有效值为

(16)

3.2 电气传动设备低频-前馈复合控制系统

通过传感器误差信号e1(t)、e2(t)以及传感器采集的信号数据u(t)，对误差信号进行优化处理并建立相应的基础函数，用Vk(q)表示。

对扰动所产生频域进行估计比对，即

(17)

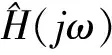
(18)

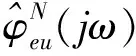
(19)

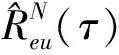
(20)

(21)

(22)

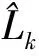
基于以上操作，对综合能源接入下电气传动设备作业时所产生的扰动信号进行控制，阻隔信号传播，降低声压，使扰动信号得到有效抑制，减小对周围环境和作业人员影响。

4 算例分析

设置一个电气传动设备监测点，对综合能源接入下的电气传动设备产生的干扰进行了测试。

4.1 不同攻角扰动抑制测试

电气设备干扰声压频谱分布结果如图1所示。

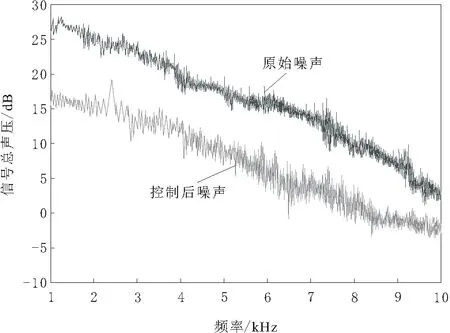
图1 水平作业时扰动抑制前后频谱

由图1可知，在水平方向上，原始扰动信号的总声压值为28.5 dB，经过文中方法控制后的干扰总声压值为17.8 dB，信号在经过控制后声压下降了37.5%，声压降低效果较为明显。

但电气设备在传动作业时，需要在不同角度变换，所产生的干扰频域和声压也不尽相同，扰动抑制技术在不同角度对干扰的控制情况也会有所不同。模拟电气传动设备在不同角度下传动作业的声压频谱分布，分别对攻角为2°、6°、10°时的扰动抑制情况进行测试并对比，如图2～图4所示。

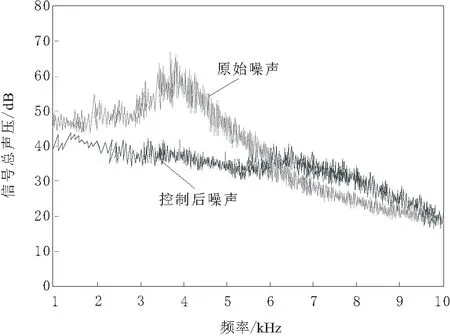
图2 攻角2°的扰动抑制前后频谱

由图2～图4可知，在3 000～6 000 Hz频率范围内，频谱图内原始扰动信号出现了类似驼峰状的尖峰波动，攻角不同时，峰值也不相同，攻角在2°、6°、10°时，原始扰动信号的波动峰值分别为69.5 dB、68.4 dB和65.2 dB，攻角增加时，原始扰动信号的驼峰状尖峰波动会随之降低，且控制后噪声的峰值皆存在不同程度的降低，扰动抑制效果明显。由此可见，攻角越来越大，驼峰状尖峰波动越来越低，扰动抑制前后频谱差异缩减，但抑制效果依旧明显，具有较优的控制性能。

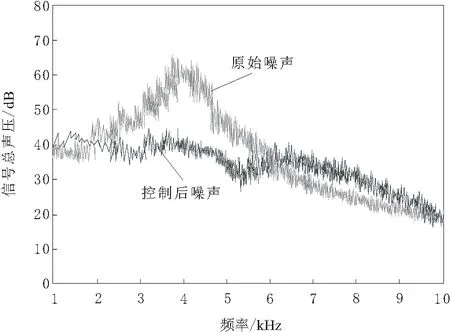
图3 攻角6°的扰动抑制前后频谱

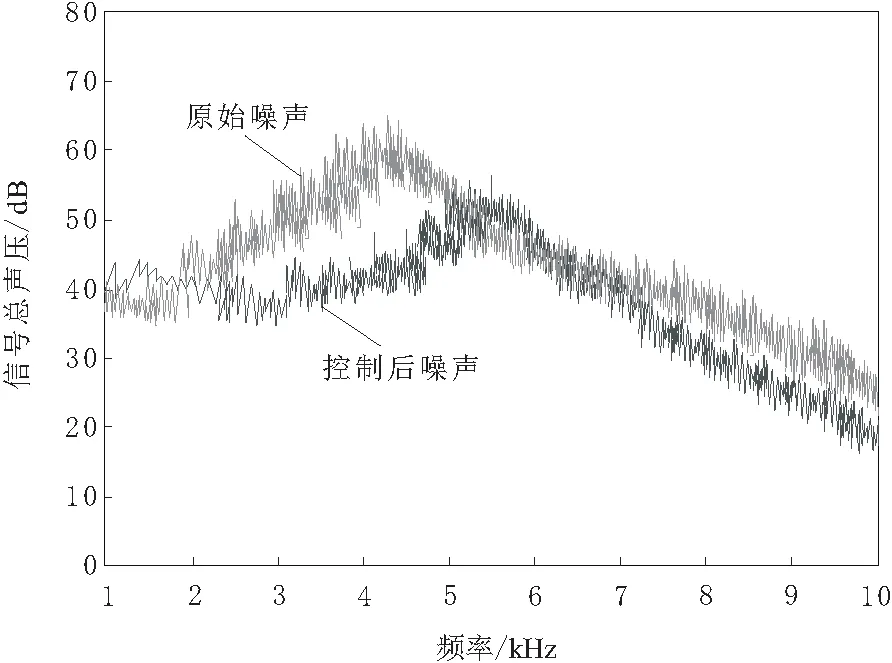
图4 攻角10°的扰动抑制前后频谱

4.2 扰动抑制效果测试

为进一步测试所提方法的有效性及吸声效果，以吸声系数为评价指标，吸声系数表示任意材料或构造对声音的吸附能力，在测试中使用相同材料，计算不同扰动抑制技术下透射过材料后干扰大小，计算不同方法的干扰吸声系数，测试结果如图5所示。

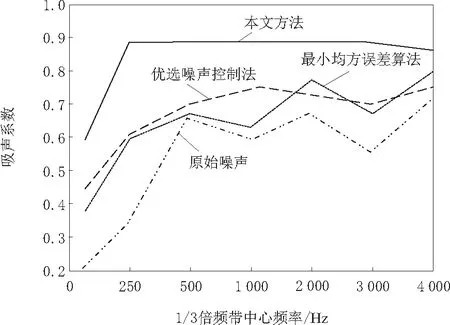
图5 吸声效果对比

由图5可知，原始扰动信号从产生开始频率迅速增加到500 Hz， 之后出现震荡上浮趋势，优选扰动抑制法在250 Hz内对干扰的控制较好，吸声效果明显，随着干扰频率越来越大时，优选扰动抑制法的吸声效果保持稳定增长，但在干扰震荡较大的情况下，并不能完全吸收干扰，最小均方误差算法的吸声效果明显不如优选扰动抑制法，在高频率干扰情况下，无法获取良好的吸声效果，反观本文方法，当干扰出现时，可以很好地控制和吸收干扰，250 Hz后吸声效果保持均匀稳定，具有很高的吸声性能，吸声效果较优。

5 结束语

提出了一种电气传动设备的低频-前馈复合控制技术，并进行了测试，可得到如下结论：

a.在传动作业的各个角度下，当电气设备受到干扰最高峰值时，扰动抑制效果依然明显，能够降低声压。

b.扰动抑制效果不受作业角度限制，吸声更加稳定，吸声系数高，吸声效果明显较优，控制性能较好。