基于IWOA-SVM的风电功率预测

王腾洲，李森文，黄宇轩，郝思鹏

(1.南京工程学院电力工程学院，江苏 南京 211167；2.电子科技大学信息与通信工程学院，四川 成都 611731)

0 引言

为实现“双碳”目标，我国大量风电机组并入电网，由于风能具有随机性和波动性等特点，大规模风电并网将会影响电网的安全性和稳定性，亟需提出准确、快速的风电功率预测方法。目前，国内外对风电功率预测的研究日趋深入，常用的方法有BP神经网络、极限学习机(extreme learning machine,ELM)和支持向量机(support vector machine,SVM)等[1]。其中，SVM由于具有结构简单、泛化能力良好和易于获得全局最优解等优点而获得广泛应用[2]。

本文针对SVM预测精度低、收敛速度慢等问题，用鲸鱼优化算法(whales optimization algorithm,WOA)对SVM的参数进行优化[3]，提高SVM的精度；同时对WOA进行改进，增加Tent混沌映射，很大程度上消除了初始种群的随机性，使初始种群在参数范围内分布更加均匀；并增加了轮盘赌方式选择猎物，在保证全局开发能力的前提下，可以依赖当前的迭代结果选择更具代表性的猎物，加快搜索收敛速度。通过算例分析结果表明，该模型具有较高的预测精度和收敛速度。

1 鲸鱼算法及其改进

1.1 基本鲸鱼算法

WOA[4]算法模仿座头鲸捕食策略，是于2016年提出的一种较为新颖的元启发式群体智能优化算法[1]。该算法寻优步骤主要有以下3个阶段。

a.包围猎物。座头鲸在捕猎过程中能迅速找到并包围猎物。其具体的数学表达式为：

D=|CL*(t)-L(t)|

(1)

L(t)=L*(t)-AD

(2)

t为当前迭代；A和C为系数向量；L*(t)为当时得到的最佳座头鲸位置向量，每一次迭代都会随着适应度大小而更新；L(t)为当前位置向量；D为当前座头鲸位置向最佳位置逼近的迭代距离。A和C的表达式为：

A=2ar1-a

(3)

C=2r2

(4)

a为参数，在搜索迭代过程中从2到0线性减少；r1和r2为[0,1]中的随机数。

b.泡网攻击。在捕猎过程中，座头鲸沿着螺旋路径向最优解移动，并缩小气泡网。其数学模型为

(5)

p为[0,1]的随机数；q为[0,1]的常数；b为常数，用于描述螺旋形状；D′为每个座头鲸与当前最佳位置的距离，D′的表达式为

D′=|L*(t)-L(t)|

(6)

c.搜索猎物。座头鲸利用它们的位置来进行随机搜索，具体过程为：

D=|CLrand(t)-L(t)|

(7)

L(t+1)=Lrand(t)-AD

(8)

Lrand为随机选择的座头鲸位置向量。

最后得到的位置向量L*即为优化选择的参数。

1.2 改进鲸鱼算法

WOA算法具有寻优能力强、结构简单和调节参数少等特点，但算法自身仍然存在着随机初始化和参数随机化会影响算法的寻优性能、种群多样性，导致算法陷入局部最优等问题。针对存在的不足，本文提出了基于Tent混沌映射和轮盘赌选择机制的改进鲸鱼算法(improved WOA，IWOA)。该算法增加了Tent混沌映射，很大程度消除了初始种群的随机性，使初始种群在参数范围内分布更加均匀；利用轮盘赌的方式选取猎物，在保证全局开发能力的前提下，可以依赖当前的迭代结果选择更具代表性的猎物，加快搜索收敛速度。

1.2.1 Tent混沌映射

Tent映射是一种分段混沌映射函数，其数学表达式为

(9)

a为[0,1]的常数。若Xn+1>1，则Xn+1返回值为1；若Xn+1<0，则Xn+1返回值为0。

Tent混沌映射得到的序列在随机性、均匀性和遍历性等方面相比于其他混沌映射具有较大的优势[5]。因此，本文采用Tent混沌映射产生的序列对种群初始化，有利于使初始的种群位置在初始解空间内分布更加均匀、范围更广[6]。

1.2.2 轮盘赌选择机制

轮盘赌选择法是一种基于比例的选择，利用各个个体适应度占所有个体适应度之和的比例决定其被选中的可能性，因此，适应度更优的鲸鱼个体被选中的几率更大。

2 支持向量机

SVM是一种基于统计学习理论的机器学习方法，当用SVM做回归预测分析时，可以通过非线性映射φ(x)函数，将低维样本x映射到更高维的向量空间Rn中，可以更好地解决小样本问题，其原理为

f(x)=ω·φ(x)+b

(10)

ω为权值系数；b为偏置项；f(x)为样本x对应的预测值。

(11)

(12)

C为惩罚参数，其值的大小代表对跳出允许拟合误差ε不敏感点的惩罚力度。

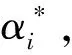
(13)

本文选取高斯径向基(radial basis function,RBF)作为模型的核函数，RBF的表达式为

(14)

δ为核函数的带宽。

3 基于IWOA-SVM风电功率预测模型

3.1 IWOA-SVM模型执行步骤

风电机组的出力大小由机组特性、风速大小和环境因素等决定，由于环境资源的多边形和风速变化具有不确定性等特点，导致了风电出力功率的不确定性[8]。

因此，本文选取风速、风向、气温、气压和空气密度这5个因素作为影响风电功率变化的主要原因，作为模型的输入量，建立风电功率预测模型。本文采用IWOA-SVM来预测风电输出功率，流程如图1所示，算法具体执行步骤如下：

图1 IWOA-SVM风电功率预测流程

a.选取训练数据和测试数据，并将数据归一化处理。

b.对WOA进行参数设置。设置种群数量、最大迭代次数和螺旋常数等，设置参数c和g的取值范围为[0.001,1 000]，选用高斯径向基作为核函数。以Tent混沌映射随机初始化鲸群的初始位置，使初始种群在参数范围内分布更加均匀。

c.以SVM的分类准确率作为适应度函数，计算每个鲸群个体的适应度，寻找并保存目前种群中最佳的鲸鱼个体位置。

d.使用WOA算法对鲸群位置进行优化，更新鲸群个体的空间位置。

e.利用适应度函数重新计算优化后各鲸群个体的适应度，采用轮盘赌的方式选取猎物，在保证全局开发能力的前提下，可以依赖当前的迭代结果选择更具代表性的猎物，加快搜索收敛速度，更新并保存当前最优的鲸鱼个体位置。

3.2 评价指标

为了更好地评估IWOA-SVM风电功率预测模型的精度，本文选用2种常用的评价指标：均方根误差(root mean square error，RMSE)和拟合优度检验系数R2，表达式为：

(15)

(16)

m为样本数；yi为测试集风电功率真实值；yavei为真实值的均值；yprei为模型预测的风电功率。上述评价指标中，R2越接近1，RMSE越小，表示模型的预测精度越好，准确度越高。

4 实例分析

为了验证本文提出的IWOA-SVM算法在风电功率预测上具有较高的精度，本文用IWOA-SVM与传统的遗传算法(genetic algorithm,GA)优化SVM和WOA-SVM在MATLAB上进行仿真对比。算例选择我国东北某地风电场在当年12月1日—31日的原始风电场数据，数据包含每5 min记录1次的风速、风向、气温、气压、空气密度和风电出力功率共8 928组数据。将12月1日--30日8 640组数据作为模型的训练样本，12月31日288组数据作为测试样本。预测结果如图2所示。

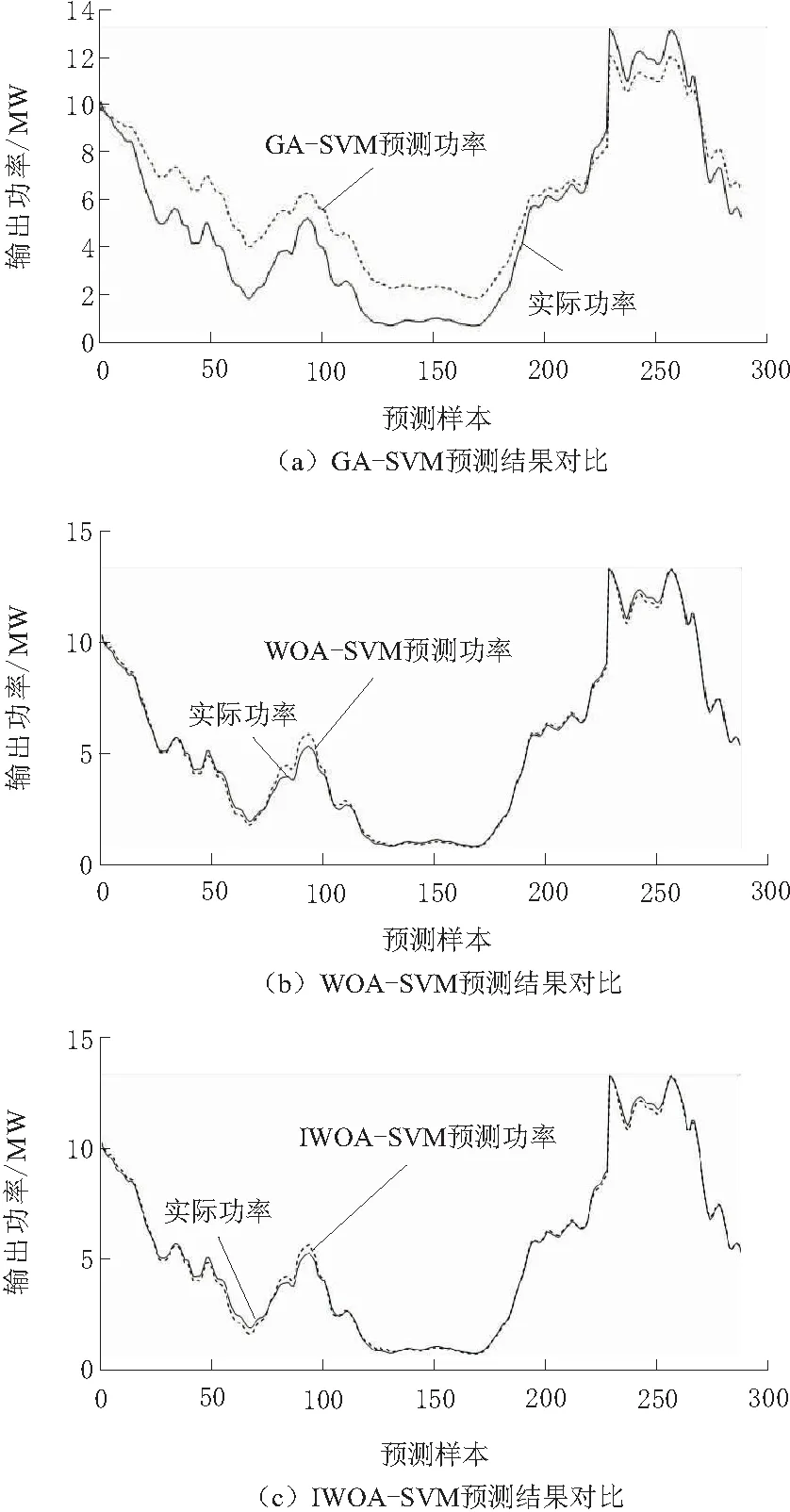
图2 3种算法预测功率和实际功率对比

由图2可知，使用WOA-SVM算法预测所得风电功率明显比传统的GA-SVM更接近实际功率，选取其中30个测试点来比较WOA-SVM和本文所提出的IWOA-SVM算法的预测结果如图3所示。

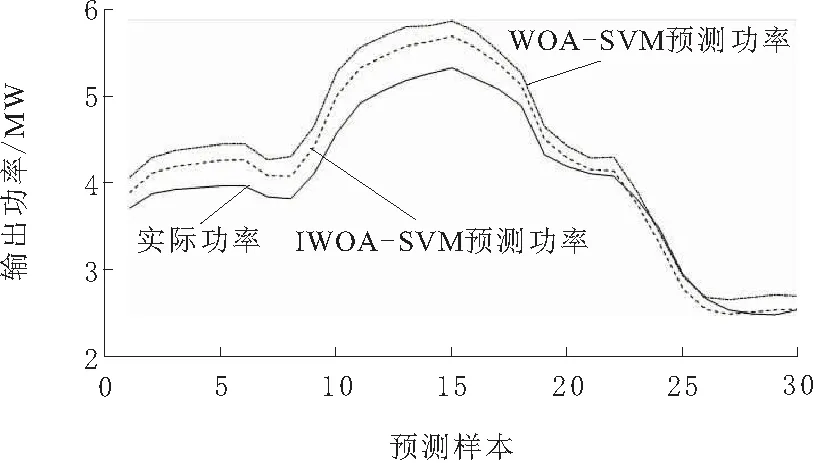
图3 WOA和IWOA-SVM预测结果对比

由图3可知IWOA-SVM有更高的预测精度。

将3种方法的预测结果和实测值按照评价指标公式进行计算、对比，结果如表1所示。

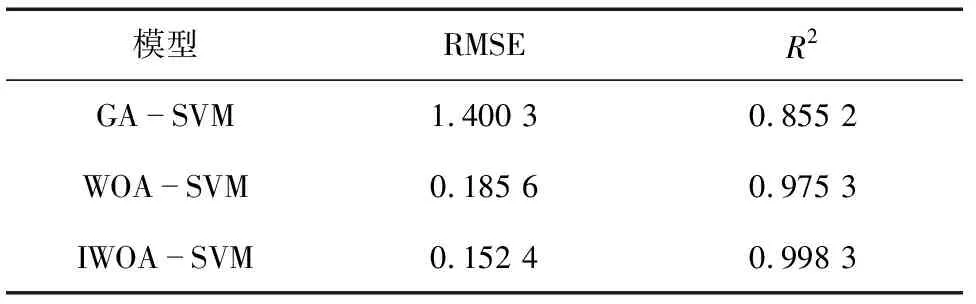
表1 评价指标结果对比

从表1可以看出，与传统GA-SVM和未改进的WOA-SVM相比，IWOA-SVM的RMSE更小，R2更加接近1，可以看出IWOA-SVM对风电功率的预测精度更高，由此可见，将Tent混沌映射和轮盘赌选择法引入WOA算法可以使SVM减小预测误差，提高预测精度。

5 结束语

本文针对SVM预测精度低、收敛速度慢等问题，用WOA算法对SVM的参数进行优化，提高了SVM的精度；同时对WOA进行改进，增加了Tent混沌映射和轮盘赌方式选择猎物以减少初始种群随机性和加快收敛速度。通过算例分析结果表明，本文提出的IWOA-SVM模型对于风电功率预测具有较高的预测精度。