隧道无人台车运动学及轨迹规划研究

胡志荣

中铁十一局集团第五工程有限公司 重庆 400037

0 引言

随着自动化控制技术的日趋进步，在隧道施工工程中对装备的自动化要求也愈发提高。因此，对隧道二衬养护起着关键作用的新型无人养护台车应运而生。该无人养护台车能在狭长隧道空间内完成自动行进、自主转向，可在养护作业时调整自身的位置姿态，对养护台车的自动控制尤为重要。

各类智能车辆的自动避障行驶、换道轨迹规划一直是当今社会研究的热点和重点。毛志伟等[1]建立了一种四轮驱动全轮差速转向的焊接机器人的转向误差模型，并用仿真的方法验证了该误差模型的精度；李玮等[2]提出了一种基于多项式理论的车轮换道轨迹规划算法，并验证了该算法的正确性及有效性；陈广锋等[3]针对仓储环境中多AGV小车的路径规划问题提出了一种基于多帧时间窗轮换算法并验证；张荣辉等[4]基于多车协同运行的情况下提出了一种无人驾驶车辆换道汇入的控制方法。上述各学者的研究大多针对差速驱动的AGV、机器人小车或是采用阿克曼转向方式的汽车等[5，6]，而对无偏转轮、四轮全驱动、差速转向的大型工程施工装备的自动行驶及调整轨迹规划[7，8]的研究不多。

本文以应用于长大隧道施工的无人养护台车为研究对象，建立了台车-隧道的三维耦合模型。通过分析其差速转向运动学，以5次多项式作为插值函数拟合其位姿调整的轨迹，使得台车检测到位姿的偏移后在不与隧道内壁碰撞的情况下智能地、自动地完成其位姿的调整，使台车回至隧道中心线，实现台车的自动行驶，达到隧道内施工少人化的目的。然后基于多体动力学软件Simpack仿真实验，模拟了台车的调整过程。最后搭建了实验小车平台来验证养护台车的轨迹规划和自动控制方法的可行性与可靠性。

1 台车模型建立及运动学分析

1.1 台车模型的建立

为了满足隧道二衬在养护作业时其他工程车辆、工程装备的正常通行，该台车摒弃常规的带差速器的阿克曼转向方式，而是采用大轮距、大轴距的差速驱动转向的轮式底盘，在台车中间留有足够的行车空间，使得养护台车能在不影响隧道施工效率和进程的情况下智能地、自动地进行养护作业。

依据工程项目的隧道断面尺寸要求以及边界条件，养护台车整体为全断面的拱形桁架结构、行走部分为四轮驱动的、无偏转轮的差速转向机构，表示台车养护作业时与隧道位置关系的三维耦合模型如图1所示。

图1 台车-隧道三维耦合模型

1.2 台车差速转向的运动学分析

图2为无偏转轮的台车差速转向时的运动学简化模型。车体的几何中心即为台车的质心，故养护台车的运动学模型可简化为几何运动问题。本文中ψ为台车姿态角，为运行方向与x轴的夹角，Vc为台车质心线速度，ωc为台车质心角速度，R为台车转向半径，d为车轮直径，VL为左侧轮线速度，VR为右侧轮线速度，ωL为左侧轮角速度，ωR为右侧轮角速度，b为轮距，xe0为台车质心的初始偏移量，L为轴距、车体外轮廓长，δ为台车外廓与隧道二衬内廓的距离。

图2 台车差速转向的运动学简化模型

在进行台车的运动学分析时，假设：台车车体整体为刚性；车轮速度方向与车轮方向相同，即假设轮胎无侧偏现象[9]；台车在低速行驶情况下侧向力极其小，即不考虑车体侧滑现象；台车的转向半径变化较缓慢，则台车姿态角ψ的变化率就近似等于台车的角速度ωc。

台车的左右侧车轮通过双出轴减速器由单个电动机同时驱动且均无偏转机构，保证了同一侧车轮的转速一致。由图2可知，Oc为养护台车差速转向的速度瞬心即转向中心，通过几何关系推导可得

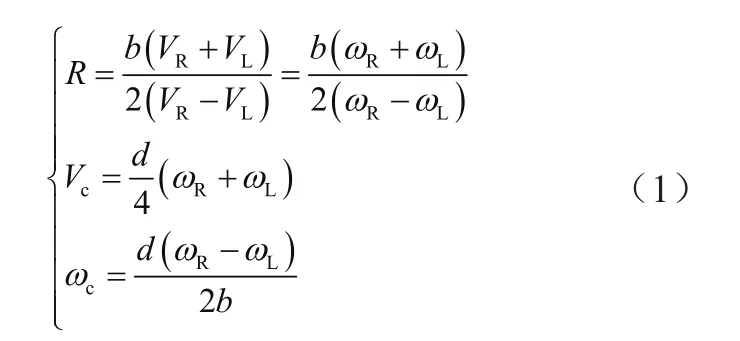
设养护台车质心在大地坐标系xOy中的位置坐标为(xc，yc)、台车前进方向与x轴的夹角（即姿态角）为ψ，则可以用向量（xc，yc，ψ）T表示台车的位置姿态。结合式(1)推导得台车质心的运动学方程为

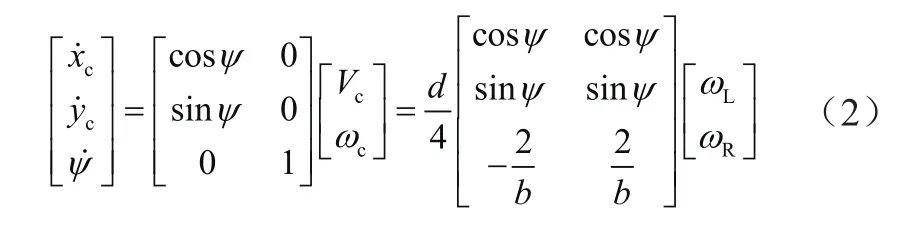
由式(2)可知，通过控制2变频电动机的输出脉冲频率，可间接地同时控制左右侧车轮的角速度ωL、ωR，在理论上可实现台车在平面内任意位置、姿态的运动。

2 台车位姿调整的轨迹规划

如图2所示，当台车位姿发生偏移后，为保证其在作业时不与隧道内廓发生碰撞，将通过传感系统将检测数据发送至PLC做出相应调整。为使台车的调整过程趋于简单可靠，将其分为2个阶段。第一阶段目的在于将台车的姿态角调整至90 °，使台车的中心线与隧道中心线平行；第二阶段目的在于通过轨迹规划，实现台车中心线与隧道中心线重合。整个过程如图3所示。

图3 台车位姿调整示意图

对于第一阶段而言，台车需要的转向角即为期望姿态角和当前姿态角的差值。在此采用的方式为定差速转向，即转向半径保持不变。

在台车中心线与隧道中心线平行后，台车的前进距离x1、横移距离y1和所需时间t1按式（3）确定

式中：ψ0为台车发生偏移的初始姿态角。

基于5次多项式的特性[10]能够描述台车轨迹上任一点的横纵向位移、速度及加速度信息，在台车的前进x和偏移y方向分别构造关于时间t的5次多项式轨迹函数为

根据台车的初始状态和目标状态即可计算得到一条光滑的姿态调整的轨迹[11,12]，定义台车的初始状态S0和目标状态St分别为

式中：x、y为台车的纵、横向位移，其一阶导为台车的纵、横向速度，其二阶导为台车的纵、横向加速度。

基于式(4)的5次多项式函数，可以定义台车第二阶段调整轨迹的时间矩阵为

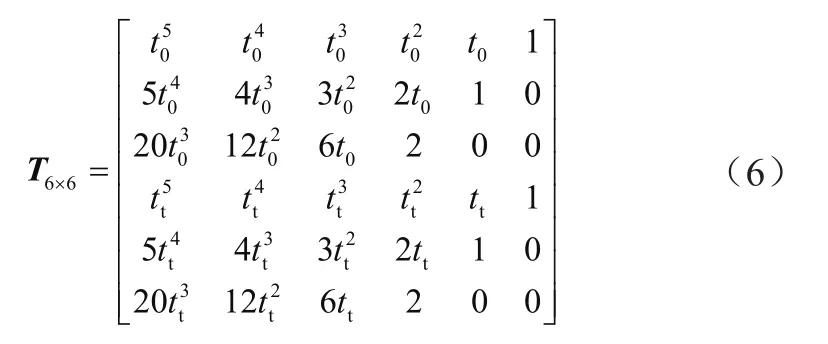
式中:t0为台车第二阶段调整开始时刻，tt为台车调整完成时刻。

在台车x和y方向上给定一组边界条件[13]，，联合式(6)求解式(7)便可得到系数矩阵A、B，再将系数矩阵中各元素值代入式(4)，即求得台车第二阶段调整的轨迹方程x(t)和y(t)。

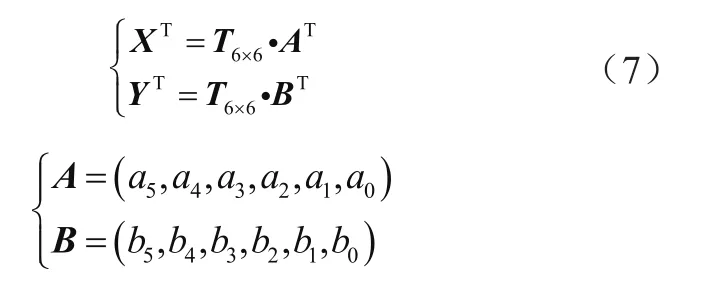
式中：A，B分别为x和y方向上台车第二阶段调整的轨迹方程的系数向量。

台车第二阶段调整的轨迹方程x(t)和y(t)具有二阶导，轨迹曲线上任意一点的曲率半径可确定

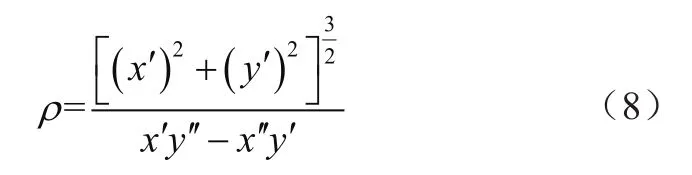
台车的转向半径即为其轨迹的曲率半径，联合式(2)将式(8)转化为关于可控参数，即车轮转速ωL、ωR的方程为

3 仿真与实验

3.1 仿真环境与条件

基于Simpack软件对台车调整过程进行运动学与动力学仿真[14]。将台车底盘与地面用20号铰接使之平行；轮毂与底盘用0号铰接约束全部自由度；车轮与轮毂用34号铰接约束5个自由度并模拟车轮转速（施加关于时间的转速函数）；车轮与地面之间用253号力元模拟实心轮胎的特性参数（垂向刚度、侧偏刚度等）。仿真模型的二维拓扑图如图4所示。

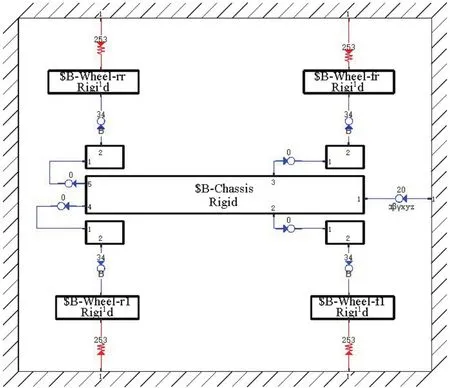
图4 多体仿真拓扑图

依据文献[15,16]研究，实心轮胎具有非线性特性，其力学性能受垂向载荷、侧偏刚度的影响较大。因此，在仿真过程中需要考虑多工况，即车轮受到不同垂向载荷的情况下对台车行驶轨迹的影响。本文主要针对车轮垂向载荷分别为20 kN、25 kN、30 kN以及40 kN 4种情况进行了仿真分析。

按照工程实际，台车关键参数为：b=5 600 mm；L=3 600 mm；d=738 mm。当台车中心线与隧道中心线重合时，δ1=δ2=δ3=1 000 mm；设定调整过程中安全余量为δ1=300 mm。台车正常行驶速度为Vc=0.2 m/s，因而台车轮胎的角速度为ωL=ωR=0.542 rad/s。台车发生偏移后假定其位姿状态为ψ0=80°，xe0=100 mm。

3.2 仿真结果及分析

如图3所示，对台车左侧车轮进行降速，实现差速转向以调整台车与隧道中心线平行，按照防碰撞和时间要求，台车调整时应满足

设定调整时间t1=20 s，联合式(3)和式(10)求解得降速后左侧车轮角速度ωL1=0.41rad/s，将车轮的转速函数输入Simpack模型进行仿真并得到在不同车轮载荷（由不同的垂向载荷引起）下的轨迹曲线对比如图5所示。

图5 不同轮载下的台车第一阶段轨迹对比图

根据第一阶段仿真的结果，台车需沿y正向偏移400 mm才可调整至隧道中心线，且根据台车的运动学、动力学特性以及控制稳定性设定在调整的始末时刻横纵向加速度均为0，故取初始、目标状态为S0=(0,0.2,0,0,0,0)，St=(6,0.2,0,0.4,0,0)。设调整时间t2=tt=40 s，求解式(7)得到系数矩阵

将系数矩阵代入式(4)求得轨迹函数，然后通过求解式(9)得到车轮关于时间的转速函数，导入Simpack进行仿真，得到台车位姿调整的轨迹曲线对比图如图6所示。

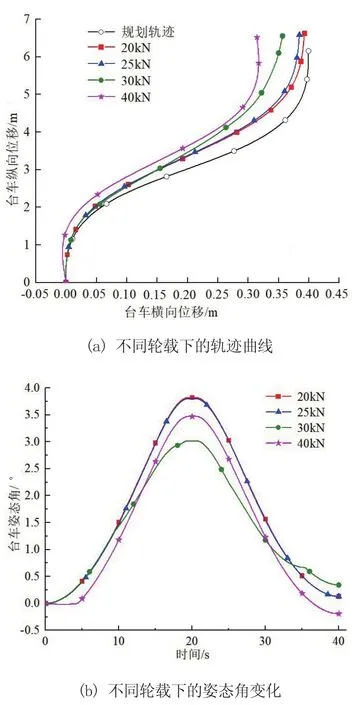
图6 台车第二阶段轨迹参数对比图

由图5可知，台车轨迹平滑无突变，在轮载为20 kN和25 kN的一般载荷情况下与规划的轨迹重合度较高，横纵向的相对偏移误差均在3%以内。但30 kN和40 kN的重载情况下轨迹出现较大偏移且呈现出非线性的变化。

由图6a可知，当轮载为20 kN和25 kN时，仿真结果基本能到达所规划的目标位置，横向相对误差约2.5%，纵向相对误差为8%；当轮载为30 kN和40 kN时，轨迹出现很大偏移，此时误差值已经不能满足要求。由图6b可知，轮载为20 kN和25 kN时，台车的姿态角变化曲线光滑无突变，表明转向平稳性较好；而30 kN和40 kN的情况下，台车姿态角变化曲线不稳定，甚至出现负角度。

由图5、图6可知，仿真结果与规划轨迹有一定的差异，在轻载的情况下，台车基本能实现所规划的轨迹行驶。随着垂向载荷越大台车并不能达到目标位置，这是因为重载情况下导致实心轮胎的变形量增大，会引起轮胎刚度的波动变化。随着台车质量的增大（反映在轮载增大）其转动惯量亦增大，机械特性响应越慢，轨迹偏移量越大，相对误差亦越大。这说明在车轮垂向载荷较大时，应当考虑台车横向动力学对轨迹规划的影响。

3.3 实验结果及分析

本文考虑到实际台车的尺寸及操作难度，故搭建了如图7所示的实验验证平台。为保证实验的高还原度，实验小车的底盘结构原理与台车一致，均为4轮驱动的、无偏转轮的差速转向轮式底盘；其行驶工况也模拟了隧道的狭长环境。

实验小车为空载状态（模拟较小的垂向载荷），设定实验的调整参数，对调整过程进行跟踪，初始姿态如图7a所示、终末姿态如图7b所示，成功实现了本文规划的轨迹行驶，通过数据采集器所采集的实验过程的速度、加速度参数经拟合后得到的曲线图如图8所示。

图7 实验平台与实验验证

图8 实验结果参数

由图8可知，在实验过程中小车的横纵向速度、加速度曲线连续且光滑，总体波动范围较低，表明稳定性和操控性较好。

4 结论

1)基于5次多项式规划的轨迹能够使得台车在发生位姿偏移后能回至隧道中心线，实现长大隧道狭长环境下无人台车的自动行驶，减少隧道内施工人员；

2)垂向载荷较小时，台车能够达到预期位姿，且相对误差较小，各项参数指标也较理想；

3)垂向载荷较大时，轮胎的变形和轮胎刚度的波动变化使得台车的动力学响应更加显著。在重载时，轨迹规划应综合考虑台车的横向动力学。