空间周期性驱动对双层耦合反应扩散系统中图灵斑图的影响*
刘倩 田淼 范伟丽 贾萌萌 马凤娜 刘富成‡
1)(河北大学物理科学与技术学院,保定 071002)
2)(河北大学环境工程研究所,保定 071002)
周期性驱动是控制斑图最有效的方式之一,因此一直是斑图动力学研究的一大热点.自然界中的斑图形成系统大多是多层耦合的非线性系统,周期性驱动对这些多层耦合系统的作用机理人们还不甚了解.本文通过耦合Brusselator (Bru)系统和 Lengyel-Epstein (LE)系统,并给LE 系统施加一个空间周期性驱动来研究外部驱动对多层耦合系统中图灵斑图的影响.研究发现,只要外部驱动与Bru 系统的超临界图灵模(内部驱动模)两者中的一个为长波模时,就可以将LE 系统中的次临界图灵模激发,3 个模式共同作用从而形成具有3 个空间尺度的复杂斑图.若外部驱动和内部驱动模均为短波模,则无法激发此系统的本征次临界图灵模,但满足空间共振时也可以产生超点阵斑图.若LE 系统的本征模为超临界图灵模,其自发形成的六边形斑图只有在外部驱动强度较大的情况下才能够产生响应,且其空间对称性受到外部驱动波数的影响.
1 引言
自组织斑图现象普遍存在于自然界及其各种时空延展非线性系统中,例如生态环境系统[1]、对流系统[2]、振荡法拉第系统[3,4]、气体放电系统[5]、化学反应扩散系统[6]等.图灵分岔被认为是斑图形成的一种重要机制,图灵不稳定性在许多斑图的形成中起到主要作用[7−9].众所周知,自然界中斑图的形成机理是复杂的,受到外界因素的调控作用,且该外界调控通常随时空发生变化.为了探究外界因素的影响机制,给系统施加一个外部时空驱动是研究这一问题的常用方法[10−20].早期,Dolnik等[13−17]在光敏二氧化氯-碘-丙二酸(CDIMA)反应扩散系统基础上分别施加一维、二维空间周期驱动,获得了迷宫斑图向六边形、四边形以及超晶格斑图转换.Haim 等[18]研究了空间周期光照下Lengyel-Epstein (LE)系统的共振空间周期解;Liu等[19]阐明了受弱信号和空间周期力作用下可激发反应扩散系统的共振集体行为.多项研究结果表明,空间周期性外部驱动对单层反应扩散系统的斑图形成具有重要影响.
实际上,不论是自然界还是非线性实验耗散系统,斑图形成大多是多层结构相互耦合、共同作用的结果[21−26].人们通过构建多层耦合系统,获得了与自然界斑图高度吻合的斑图类型.例如,Barrio等[21]建立双层耦合反应扩散系统,获得了与自然界中鱼的体表图案十分接近的斑图结构.Li 等[22]在双层LE 反应扩散模型中获得了四边形图灵斑图.Paul 等[23]通过对双层反应扩散系统的参数调控理论分析了反相同步和时空斑图形成的机理.李伟恒等[24]在双层介质中分别采用抑制和兴奋性耦合,研究了双层可激发介质中的螺旋波动力学.前期工作中,本课题组[26]通过线性耦合Brusselator(Bru)模型与LE 模型反应扩散系统,研究了两个图灵模之间的相互作用,分析了斑图选择和形成的影响因素.上述工作表明,采用具有双层及以上多层耦合系统来描述自然界中斑图的形成机理更为准确和充分.特别是,如果在多层耦合系统基础上,能够考虑到外界时空驱动对斑图形成的影响,无疑更加贴近实际、更加具有普适性和广泛性.在双层扩散耦合光敏CDIMA 化学反应中,Miguez 等[27]通过光照周期性透光性掩膜实现外部调控对自组织斑图的扰动,研究了两层图灵模式之间的相互作用.白婧等[28]采用神经元模型研究了具有多个长方形长程耦合区的神经元网络中波的传播,获得了局部同步引发的各种效应.李倩昀等[29]构造了由心肌细胞和成纤维细胞组成的双层复合介质,通过细胞之间的耦合强度实现了复合介质中的螺旋波和时空混沌的控制.张秀芳等[30]基于光电管耦合两个FitzHugh-Nagumo (FHN) 神经元,实现了耦合系统在外界光照辐射注入能量后的动力学行为控制.作为一种特殊的多层耦合反应扩散系统,介质阻挡放电在周期性放电参数调控下,呈现出了丰富的多尺度时空斑图[31−34].例如Sinclair 和Walhout[32]采用四边形周期阵列电极获得了具有不同集体行为的放电丝结构.本课题组通过金属网栅阵列电极[33]以及周期性结构的电介质[34]实现了对等离子体斑图的空间周期性调控,并获得了不同对称性、不同结构的丰富的斑图.然而,由于机制复杂,外界时空驱动对多层耦合系统中非线性斑图形成的影响机制目前仍不十分明确.
针对介质阻挡放电系统,本文采用双层耦合Bru 系统与LE 系统,研究了外加空间周期性驱动下,不同类型斑图的形成机制.分析了空间周期性驱动强度、波长等参量对图灵斑图形成的调控作用和演化行为的影响.研究结果为我们更深入地理解斑图形成过程、揭示自然奥秘提供一定支持和启示.
2 计算模型
研究表明,气体放电系统中的放电等离子体斑图可以通过反应扩散模型唯象地描述[35,36].介质阻挡放电系统由放电层和电介质层组成,当放电产生的空间电荷移动到电介质表面后会积累形成表面电荷,反过来表面电荷形成的电场会直接影响空间电荷的行为.为了研究周期性驱动下介质阻挡放电系统中的斑图形成机理,本文构建了一个唯象的双层线性耦合反应扩散模型.在无量纲的情况下,其一般形式为
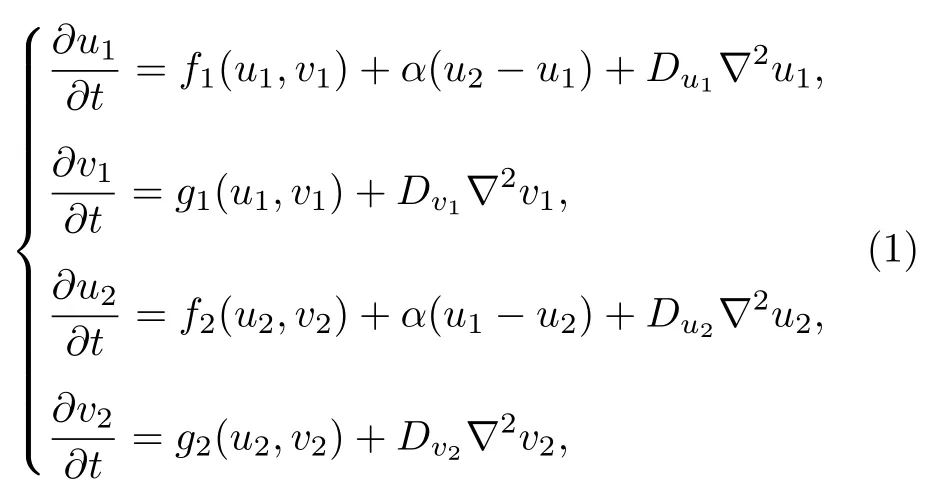
式中,u和v分别为系统内活化子和禁阻子浓度,分别对应放电系统中的电荷和电压降;Du和Dv为对应的扩散系数,下标 1,2 代表不同层子系统.耦合项α(u2−u1)和α(u1−u2)代表了空间体电荷和表面电荷之间的相互转变,其中α为两个子系统活化子(电荷)之间的耦合强度,为了方便,在整个模拟过程中选取α=0.1.本模型也可以描述通过层间扩散耦合的双层化学反应扩散系统[27].方程f(u,v)和g(u,v)是系统的局部动力学方程,不同的系统有着不同的动力学行为.由于放电系统中放电层和电介质层具有显著不同的动力学行为,本文分别选用Bru 系统和LE 系统来唯象地描述放电层和电介质层.在无量纲的情况下,Bru 系统的局部动力学为
LE 系统局部动力学为
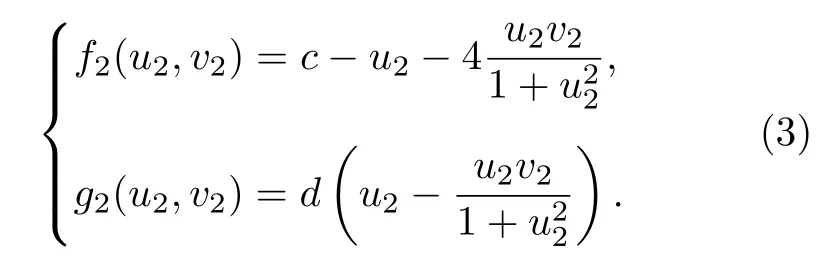
这里a,b和c,d为各个子系统的控制参数.对于Bru 和LE 子系统,其均匀定态解分别为(u10,v10)=.本文中选取c=5a,则双层耦合系统的均匀定态解可以表示为
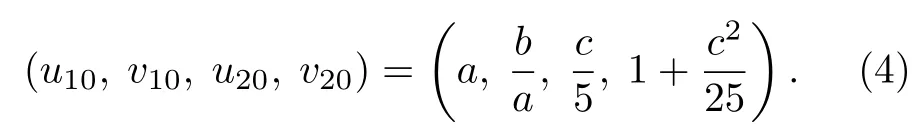
在介质阻挡放电系统中,可以通过周期性阵列电极以及周期性变化的电介质来控制放电斑图的行为.在本模型中,借用LE 系统中的光敏特性来实现这一调控.即在LE 系统中施加一个空间上呈六边形分布的周期性外界驱动w来表征外界条件的空间干扰.该驱动对系统的影响通过周期性地改变空间光照来实现,其具体表达式为
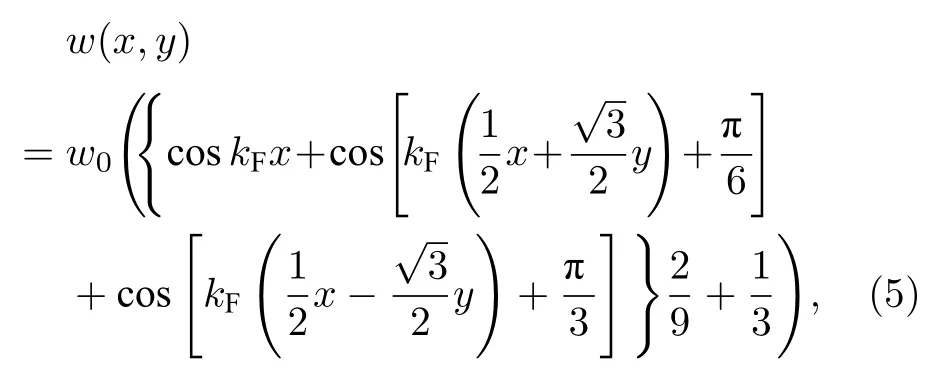
光照强度与3 个余弦函数的和成正比,其中w0和kF分别为空间周期性光照的强度和空间波数.
模拟中,采用欧拉向前差分方法进行积分.方程计算在一个含有N×N格点的二维平面上进行,边界条件选用零流边界条件.初始条件为在均匀定态解的基础上施加一个很小的随机扰动,数值算法的详细描述可参见文献[26].所有计算结果的积分时间均超过1000 个时间单位,以确保结果的稳定性.
根据耦合系统中图灵模不同的性质,将该耦合系统分为3 个类型,其相应的色散关系如图1 所示.图中用k1和kC分别表示Bru 子系统和LE 子系统中图灵模的波数.类型I 为超临界图灵长波模与次临界图灵短波模相互作用(图1(a));类型II为超临界图灵短波模与次临界图灵长波模相互作用(图1(b));类型III 为两个超临界图灵模之间相互作用(图1(c)).针对这3 种类型系统,本文分别研究了空间周期性驱动的强度w0和波数kF对斑图形成的影响.为了简便起见,不作特殊说明时,设置长波模的波数为 0.2,短波模的波数为 0.4.
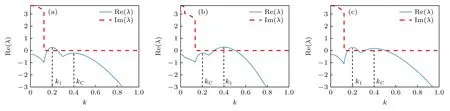
图1 不同图灵模类型的双层耦合系统的色散关系图 (a) 类型I (,α=0.1);(b) 类 型II (,α=0.1);(c) 类 型III (,α=0.1)Fig.1.Dispersion curves of two-layer coupled systems with different Turing mode types:(a) Type I (,α=0.1); (b) type II (,α=0.1); (c) type III(,α=0.1).
3 结果与讨论
3.1 类型I 耦合模式下外界驱动的强度和波数对斑图的影响
图2 研究了类型I 图灵模式下外界驱动强度对斑图的影响.设置k1=0.2,kC=0.4,kF=0.1 不变,此时子系统LE 的本征模式为次临界短波模,研究驱动强度对LE 子系统中斑图的影响.当没有外界驱动,即w0=0 时,LE 子系统自发形成白眼超六边形斑图(图2(a)),其中心有一个较高浓度的斑点,该斑点被一个低浓度环包围,外围排列着6 个高浓度的亮点,整体也呈现六边形阵列结构.由其傅里叶频谱图得出,该超六边形斑图具有两个空间尺度,分别为k1和kC,表明在类型I 耦合形式下,次临界图灵模kC在k1的作用下已经被激发.该结果与其他双层耦合模型中获得的斑图一致[37,38].此时给系统LE 施加一个波长较大的空间周期性驱动,当驱动强度很小,即w0=0.1 时,LE 子系统形成雪花斑图I (图2(b)).根据其傅里叶频谱图得出该斑图由3 套不同波数的模式组成,分别是波长最小的kC、波长较大的k1及波长最大的外加驱动kF,但是强度最强的是模式k1,最弱的是本征模式kC,这3 种模式强度相当.除此以外,模式k1和kC相互作用产生了新模式q,其强度弱于其他模式,3 个模式之间满足三波共振关系,即k1+kC=q.新模式q具有两套不同方向的六边形结构,通过几何关系可知,此两套六边形之间的夹角为θ=21.8°.这些模式共同相互作用从而形成了一个具有3 种空间尺度的超六边形点阵斑图.驱动模式kF的强度随着驱动强度的增加而增强,并成为最主要的模式.当w0=0.5 和 1.0 时,子系统LE 形成了菱形网格斑图I (图2(c))和II (图2(d)),该斑图的本征波长与外部驱动的波长相同.分析它们对应的傅里叶频谱图发现,w0增加时,子系统LE 中模式k1的相对强度稍微有所减弱,但其本征模式kC仍在增强.这是因为外部驱动直接作用于LE 子系统,作为驱动模式kF的高阶谐波,本征模式kC也随之增强.

图2 类型I 下不同驱动强度的图灵斑图及其傅里叶频谱图 (a) 超六边形斑图,w0=0;(b) 雪花斑图I,w0=0.1 ;(c) 菱形网格 斑图I,w0=0.5;(d) 菱形网格斑图II,w0=1.0(超临界图灵模 k1=0.2,次临界本征模 kC=0.4,驱动的波数 kF=0.1;N=256,Δx=Δy=1)Fig.2.Patterns and Fourier spectrum with different forcing intensity in type I:(a) Super-hexagon pattern,w0=0 ;(b) snowflake pattern I,w0=0.1;(c) rhombus mash pattern I,w0=0.5;(d) rhombus mash pattern II,w0=1.0 (Supercritical Turing mode k1=0.2,subcritical eigenmode kC=0.4 ,wavenumber of forcing kF=0.1 ; N=256 ,Δx=Δy=1).
图3 分析了空间驱动波数对斑图的影响,仍保持k1=0.2,kC=0.4 不变,且固定驱动强度,w0=0.1,逐步改变外加驱动的波数kF.当kF=0.2 时,子系统LE 形成的是超六边形斑图(图3(a)),该斑图由6 个高浓度的线状亮点包围一个暗点构成.对比图2(a)可以发现,当kF=k1时,斑图内部长波模的强度得到叠加,远高于kC的强度,导致子系统LE的斑图选择发生变化.当kF=0.4 时,子系统LE 形成的是简单六边形蜂窝斑图(图3(b)).对比图2(a)可以发现,kF=kC时,系统内部本征模的强度得到叠加,远高于k1的强度,因此,LE 子系统的斑图选择再次发生变化.当kF=0.6 时,系统LE 形成的是六边形网格斑图I (图3(c)).当kF=0.8 时,系统LE 形成的是六边形网格斑图II (图3(d)).对于后两种斑图,由于外部驱动的波数大于系统的本征模,使得它很难通过空间共振的方式激发本征模,因此六边形网格斑图主要是由模式k1和模式kF相互作用而成.
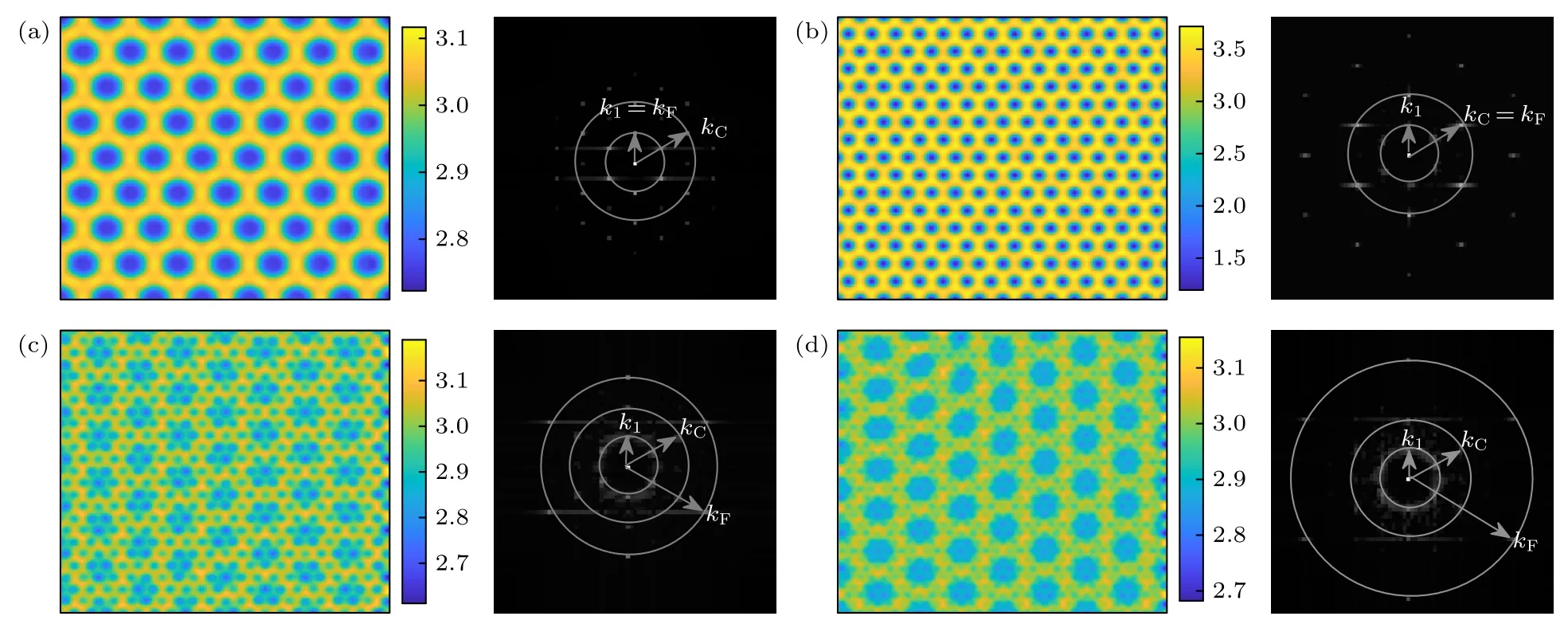
图3 类型I 下不同驱动波数的斑图及其傅里叶频谱图 (a) 超六边形斑图,kF=0.2;(b) 简单六边形蜂窝斑图,kF=0.4 ;(c) 六边形网格斑图I,kF=0.6;(d) 六边形网格斑图II,kF=0.8(超临界图灵模 k1=0.2,次临界本征模 kC=0.4,驱动的强度恒为 w0=0.1,N=256,Δx=Δy=1)Fig.3.Patterns and Fourier spectrum with different forcing wavenumber in type I:(a) Super-hexagon pattern,kF=0.2;(b) simple hexagonal honeycomb pattern,kF=0.4;(c) hexagonal mash pattern I,kF=0.6;(d) hexagonal mash pattern II,kF=0.8 (Supercritical Turing mode k1=0.2,subcritical eigenmode kC=0.4,forcing intensity w0=0.1,N=256,Δx=Δy=1).
为了对比研究外部驱动模式与Bru 系统图灵模式对LE 系统本征模的影响,将两者的波数置换,即令k1=0.1 ,kF=0.2,同时保持kC=0.4,此时系统的色散关系如图4(a)所示.图4(b)—(e)给出了不同驱动强度下获得的各种斑图.未加外加驱动,即w0=0 时,系统LE 形成的简单六边形蜂窝斑图(图4(b))是由系统Bru 的失稳模调制形成,从其傅里叶变换频谱可以看出斑图只有k1一套结构.这是因为k1:kC=1:4,两个模式之间不满足空间共振关系,因此kC并没有被激发.当驱动强度w0=0.1时,发现系统LE 呈现雪花斑图II (图4(c)).根据其傅里叶频谱图得出该斑图仅由两套不同波长的模组成,即k1和kF,由于外部驱动太弱,本征模kC依然没有被激发.继续增加驱动强度,当w0=0.6时,kC被激发,尽管系统LE 呈现简单六边形蜂窝斑图(图4(d)),但是其对应的傅里叶频谱图显示该斑图具有3 个空间尺度.当w0=1.0 时,此时kF的贡献最大,其次是本征模kC,它们满足空间共振关系,系统LE 表现为六边形白眼斑图(图4(e)).这就意味着无论是不同层之间的内部作用还是外部直接驱动,当满足空间共振关系时,都可以激发次临界图灵模kC,从而形成超点阵斑图.不同的是,达到相同效果所需要的外部驱动强度要比层间相互耦合强度要强.

图4 波数反转后不同驱动强度下的斑图及其傅里叶频谱图 (a) 色散关系图(k1 :kC=1:4,=195,=510,=6.6,=81,α=0.1);(b) 简单六边形蜂窝斑图,w0=0;(c) 雪花斑图II,w0=0.1;(d) 简单六边形蜂窝斑图,w0=0.6;(e) 六边形白眼斑图,w0=1.0(驱动的波数 kF=0.2;N=256,Δx=Δy=1)Fig.4.Patterns and Fourier spectrum of different forcing intensity after wavenumber inversion:(a) Dispersion curve (k1:kC=1:4,=195,=510,=6.6,=81,α=0.1);(b) simple hexagonal honeycomb pattern,w0=0;(c) snowflake pattern II,w0=0.1;(d) simple hexagonal honeycomb pattern,w0=0.6;(e) hexagonal white-eye pattern,w0=1.0(Wavenumber of forcing kF=0.2,N=256,Δx=Δy=1).
3.2 类型II 耦合模式下外加驱动对斑图的影响
研究表明,波数大小在模式相互作用过程中起着非常关键的作用.一般来说,只有长波模式才能激发短波模式.3.1 节讨论了超临界长波模与次临界短波模的耦合系统情况,本小节研究超临界短波模与次临界长波模耦合系统中外部驱动对斑图的影响.为了对比研究驱动波数的影响,分为短波驱动和长波驱动两种情况来讨论.
首先,对于短波驱动的情况,保持k1=0.4,kC=0.2 不变,令kF=0.8,在不同外界驱动强度下,子系统LE 中产生的斑图如图5 所示.当w0=0 时,系统LE 自发形成了简单六边形蜂窝斑图(图5(a)),该斑图完全是由子系统 Bru 的失稳模调制形成.正如其傅里叶频谱图所示,该斑图只有一种空间模式k1.当驱动强度很弱,即w0=0.1 时,系统LE 仍表现为简单的蜂窝六边形(图5(b)),但是根据其傅里叶频谱图可以看出,该简单蜂窝六边形由k1和kF两套结构组成,由于驱动强度较小,所以k1占主导位置,因此斑图形状变化不明显.继续增加驱动强度,当w0=0.5 时,模式k1的强度只是稍大于模式kF,系统LE 形成六边形花瓣斑图I (图5(c)),即模式kF对原斑图具有很明显的调制作用.当w0=1.0 时,模式kF的强度与k1相同,六边形花瓣斑图I 转变为了六边形花瓣斑图II (图5(d)).值得说明的是,在整个过程中,kC始终未被激发.这意味着无论短波模是内部产生还是外部施加,都无法激发出次临界长波模kC.上述结果表明仅仅是外部模式之间的相互作用,也可以在系统内产生多尺度时空斑图.

图5 类型II 下不同短波驱动强度的斑图及其傅里叶频谱图 (a) 简单六边形蜂窝斑图,w0=0;(b) 简单六边形蜂窝斑图,w0=0.1;(c) 六边形花瓣斑图I,w0=0.5;(d) 六边形花瓣斑图II,w0=1.0(超临界图灵模 k1=0.4,次临界本征模 kC=0.2,驱动的波数 kF=0.8,N=128,Δx=Δy=0.5)Fig.5.Patterns and Fourier spectrum of different short-wave forcing intensity in type II:(a) Simple hexagonal honeycomb pattern,w0=0;(b) simple hexagonal honeycomb pattern,w0=0.1;(c) hexagonal petal pattern pattern I,w0=0.5 ;(d) hexagonal petal pattern pattern II; w0=1.0(Supercritical Turing mode k1=0.4,subcritical eigenmode kC=0.2,wavenumber of forcing kF=0.8,N=128,Δx=Δy=0.5).
接下来讨论长波外部驱动对类型II 系统斑图的影响.依然保持k1=0.4,kC=0.2 不变,取kF=0.1.由于长波的空间尺度较大,这里取系统的尺度为 256×256.无驱动时,系统LE 依然形成的是简单六边形蜂窝斑图(图6(a)).当驱动强度w0=0.1 时,蜂窝六边形的空间分布受到驱动kF的调制使得其强度分布呈现周期性分布(图6(b)),调制波长与外加驱动波长相等.通过其傅里叶频谱图可知,kF的强度几乎是k1模式的两倍,即模式kF起主导作用.继续增加外加驱动的强度至w0=0.6,此时子系统LE 的本征模kC被激发,且其强度稍高于模式k1,3 个模式之间相互作用,形成了六边形蜂窝斑图,如图6(c)所示.当w0=1.0时,受到kF的激发作用,kC和k1的强度均有所增加,子系统LE 中形成了明显具有3 个空间尺度的黑眼六边形蜂窝斑图(图6(d)),该斑图与类型I 中的六边形网格斑图II 类似(图3(d)).
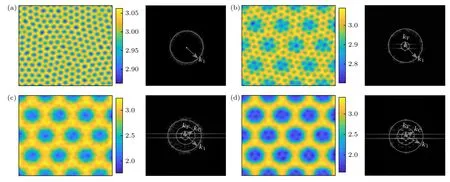
图6 类型II 下不同长波驱动强度的斑图及其傅里叶频谱图 (a) 简单六边形蜂窝斑图,w0=0;(b) 简单六边形蜂窝斑图,w0=0.1;(c) 六边形蜂窝斑图,w0=0.6;(d) 黑眼六边形蜂窝斑图,w0=1.0(超临界图灵模 k1=0.4,次临界本征模 kC=0.2,驱动的波数 kF=0.1,N=256,Δx=Δy=1)Fig.6.Patterns and Fourier spectrum of different long-wave forcing intensity in type II:(a) Simple hexagonal honeycomb pattern,w0=0;(b) simple hexagonal honeycomb pattern,w0=0.1;(c) hexagonal honeycomb pattern,w0=0.6;(d) black-eye hexagonal honeycomb pattern,w0=1.0(Supercritical Turing mode k1=0.4,subcritical eigenmode kC=0.2,wavenumber of forcing kF=0.1,N=256,Δx=Δy=1).
3.3 类型III 耦合形式下外加驱动对斑图形成的影响
接下来研究两个超临界图灵模作用的情况.首先固定驱动波数kF=0.1 不变,驱动强度对子系统LE 斑图的影响如图7 所示.这里依然选择k1=0.2,kC=0.4.此时子系统LE 的本征模式为超临界短波模.w0=0,即不加周期性空间驱动时,系统自发产生的是简单六边形蜂窝斑图(图7(a)).尽管子系统Bru 中的图灵模是一个失稳模,但是它对LE层斑图的影响非常小,在其傅里叶变换频谱仅仅能够看到强度非常弱的k1.
当驱动强度较小,即w0=0.1 时,系统LE 仍表现为简单的蜂窝六边形(图7(b)),尽管从其傅里叶频谱图可以看出该斑图包含k1,kC和kF三种成分,但由于外加驱动的影响相对较弱,对斑图的形状影响并不明显.继续增加外加驱动的强度至w0=0.5,蜂窝六边形开始受到外部驱动的调制,如图7(c)所示,在调制部分开始出现条纹斑图.当驱动强度足够强(w0=1.0)时,子系统LE 形成了条纹和蜂窝六边形共存的斑图(图7(d)).在驱动强度增大的过程中,k1的强度始终较弱,kF的强度在逐渐增强,并逐渐影响斑图的周期性,最终改变其对称性.

图7 类型III 下不同驱动强度的斑图及其傅里叶频谱图 (a) 简单六边形蜂窝斑图,w0=0;(b) 简单六边形蜂窝斑图,w0=0.1;(c) 调制蜂窝斑 图,w0=0.5;(d) 条纹与蜂窝六边形共存斑图,w0=1.0(超临界图灵模 k1=0.2,超临界图 灵模kC=0.4,驱动的波数 kF=0.1;N=128,Δx=Δy=1)Fig.7.Patterns and Fourier spectrum with different forcing intensity in type III:(a) Simple hexagonal honeycomb pattern,w0=0;(b) simple hexagonal honeycomb pattern,w0=0.1;(c) modulated honeycomb pattern,w0=0.5;(d) coexistence of stripe and honeycomb hexagon,w0=1.0(Supercritical Turing mode k1=0.2,supercritical Turing mode kC=0.4,wavenumber of forcing kF=0.1,N=128,Δx=Δy=1).
由于空间驱动只有在强驱动强度下才对斑图有作用,因此下面研究强驱动强度下不同驱动波数对斑图的影响.固定驱动强度w0=1.0,并依然保持k1和kC不变,获得的结果如图8 所示.当kF=0.2时,子系统LE 形成的是点和线共存的不规则复杂斑图(图8(a)).此斑图对应的傅里叶频谱图中包含一个尺度为kF=k1的六边形点阵以及一个尺度为kC的圆环,且两者的强度几乎相同.由于外部驱动kF和内部驱动模式k1波数相同,因此两者共振叠加,形成了六边形结构.而对于本征模kC,强驱动改变了其对称性,从原来的六边形转变为了条纹斑图,同时其空间取向具有随机性,因而形成了方向各异的条纹结构.当kF=0.4 时,子系统LE形成的是简单六边形蜂窝斑图(图8(b)),这是由于此时kF=kC,本征模kC的强度共振叠加,远高于k1的强度,斑图只表现为kF=kC的空间尺度.当kF=0.6时,系统LE 形成的也是简单六边形蜂窝斑图(图8(c)),斑图的空间尺度与外加驱动一致,此时外加驱动对斑图的调控占主导作用.当kF=0.8 时,系统LE 中呈现具有本征波数kC的条纹斑图(图8(d)),也就是说在外部驱动作用下斑图打破了原本六边形的空间对称性,转变为了条纹斑图.
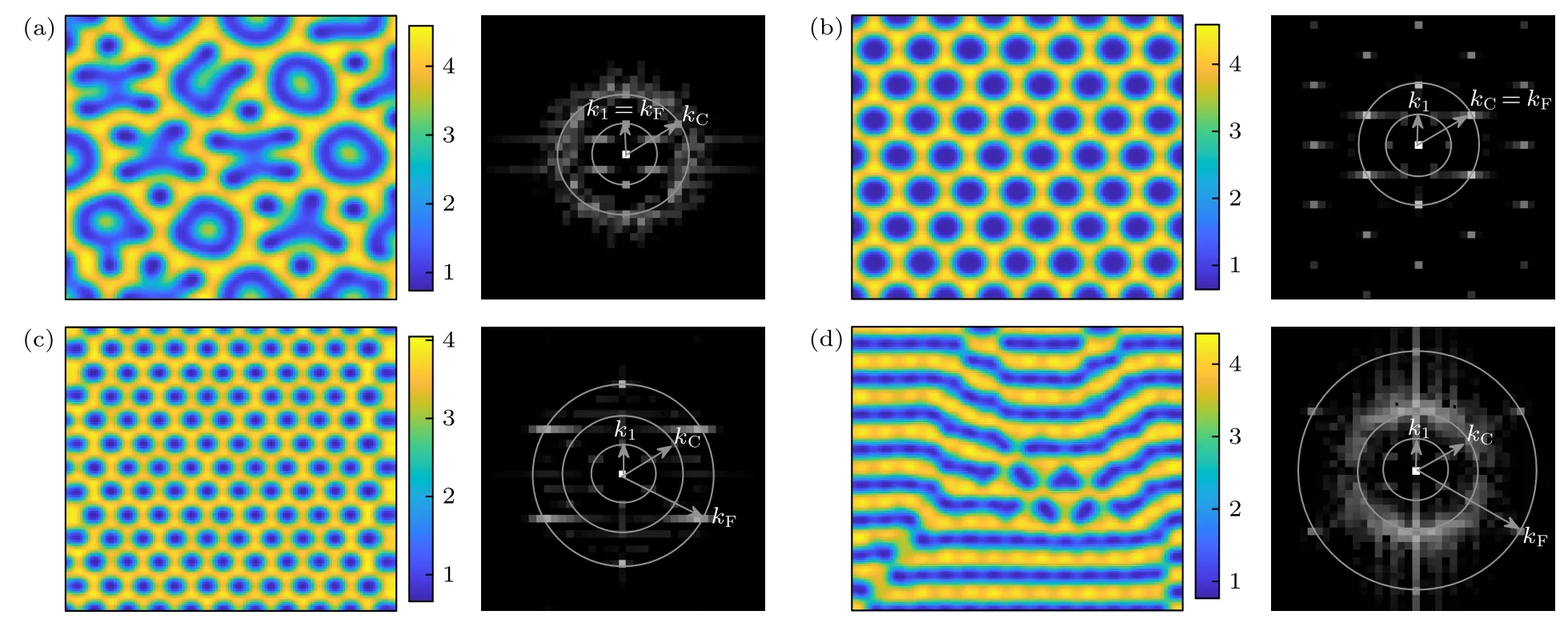
图8 类型III 下不同驱动波数的斑图及其傅里叶频谱图 (a) 复杂斑图,kF=0.2;(b) 简单六边形蜂窝斑图,kF=0.4;(c) 简单六边形蜂窝斑图,kF=0.6;(d) 条纹斑图,kF=0.8(超临界图灵模 k1=0.2,超临界图灵模 kC=0.4,驱动的强度固定为w0=1.0,N=128,Δx=Δy=1)Fig.8.Patterns and Fourier spectrum with different forcing wavenumber in type III:(a) Complex pattern,kF=0.2;(b) simple hexagonal honeycomb pattern,kF=0.4;(c) simple hexagonal honeycomb pattern,kF=0.6;(d) stripe pattern,kF=0.8 (Supercritical Turing mode k1=0.2,supercritical Turing mode kC=0.4 ,forcing intensity w0=1.0,N=128,Δx=Δy=1).
与前两种类型不同,类型III 中LE 系统的本征模是一个失稳模,能够自发形成六边形斑图,该斑图只有在外部驱动强度较大的情况下才能够对驱动产生响应,且随着外加驱动波数的改变,空间对称性也发生了改变.
4 结论
本文通过耦合两个不同的反应扩散系统,即Bru 系统和 LE 系统,并给其中的LE 系统施加一个空间周期性外部驱动,研究了周期性空间驱动对双层耦合系统斑图形成的影响.保持Bru 系统中的图灵模为超临界模,根据LE 子系统图灵模的性质不同,将耦合系统分成了3 种类型,它们在外部空间驱动作用下的行为有很大不同.
1)当LE 子系统中的图灵模为次临界短波模时,系统自发形成双尺度的白眼超六边形斑图.在周期性外部驱动作用下,超临界图灵模和次临界图灵模以及驱动模三者共同作用,可以形成具有3 个空间尺度的复杂斑图.驱动强度和驱动波数对斑图类型的选择影响很大.研究发现不论是内部作用还是外部直接驱动,当满足空间共振关系时,都可以激发次临界图灵模kC,从而形成超点阵斑图,但是达到相同效果所需要的外部驱动强度要比层间相互耦合强度要强.
2)当LE 子系统中的图灵模为次临界长波模时,系统仅仅受到Bru 层图灵短波模的调制而形成微弱的简单的六边形斑图.当外部驱动也为短波模时,只有两个短波模之间相互作用,无法激发次临界长波本征模.而当外部驱动为长波模时,LE系统中的次临界本征模被激发,3 个模式之间可以共同作用而形成3 个尺度的超点阵斑图.
3)当LE 子系统中的图灵模为超临界图灵模时,系统自发形成由本征模构成的简单六边形斑图,此时Bru 层中的图灵模以及弱外部驱动模仅仅起到一个非常微弱的调制作用.只有在外部驱动强度较大的情况下才能够对系统的斑图产生影响,且随着外加驱动波数的改变,原来的空间对称性被打破,斑图类型从六边形斑图转变成了条纹斑图.

