中国大陆GPS连续站时间序列噪声分析
郑博文,杜向峰,詹松辉,吴希文,王 华
(1. 广东工业大学 土木与交通工程学院, 广东 广州 510006;2. 广东工贸职业技术学院 测绘遥感信息学院, 广东 广州 510510)
目前,利用GPS位置时间序列估计速度已广泛用于研究地表形变、板块运动等[1-2],然而GPS速度值的精度如何评定尚需探讨[3-5]。由于GPS位置时间序列中不仅含有随机噪声(白噪声),还含有与时间相关的噪声。如果只使用纯白噪声模型,速度的精度会被严重高估。大量研究表明,仅用纯白噪声模型进行精度估计,速度的精度会被高估3~38倍[6-13]。因此,必须采用正确的噪声模型来估计GPS速度的精度。本文以“中国地壳运动观测网络”和“中国大陆构造环境监测网络”(CNONOC-I/II)所有GPS连续站的坐标时间序列为基础,利用极大似然估计法和频谱分析法计算其光谱指数,同时采用白噪声+幂律噪声(White Noise+Power Law Noise, WN+PL)、白噪声+闪烁噪声(White Noise+Flicker Noise, WN+FN)和白噪声+闪烁噪声+随机游走噪声(White Noise+Flicker Noise+Random Walk Noise, WN+FN+RW)等模型计算了速度的不确定性,并绘制了陆态网络连续站的速度场。
1 数据来源与GPS时间序列解算
本文使用了CMONOC-I/II共264个GPS连续站的数据。其中CMONOC-I是从1999年观测至今的27个连续站点,CMONOC-II于2009年开始观测,共有237个连续站点[1-2];时间跨度在4~9 a的有59个测站,10 a及10 a以上的有205个测站,如图1所示。本文使用武汉大学的PANDA软件进行解算[14],采用精密单点定位模式获取所有测站的单日解。在解算中,先后进行了接收机差分码偏差改正、地球自转改正和相对天线相位中心模型改正,具体解算的参数参见文献[2]的表1。

图1 GPS连续站分布图Fig.1 Map of GPS continuous station distribution
2 基本原理与方法
基于GPS坐标时间序列,利用加权最小二乘法和极大似然估计方法计算测站的速度及其不确定性。先对原始观测值进行粗差及异常阶跃的改正,获取干净的时间序列。随后通过单位权阵获取观测值的改正值,根据改正值和选取的噪声模型采用极大似然估计获取最适合描述观测值的协方差矩阵。最后通过确定的协方差矩阵计算出正确的测站速度及其不确定性。
2.1 粗差及异常阶跃检测
GPS观测值常常由于野外测量中出现的突发状况(如地震、接收机故障等)出现异常。因此本文使用式(1)所示的中位数和四分位范围(Interquartile Range, IQR)统计[15]来确定粗差,再利用地震目录中的地震时刻检测时间序列中由地震引起的阶跃,其余未知的阶跃使用改进的启发式分割算法进行阶跃探测[16]。图2为YANC测站的时间序列图,其中绿色为正常点,黑色为粗差点,橙色为探测出的阶跃。

图2 YANC测站原始坐标序列(绿色为正常点,黑色为粗差点,橙色竖线为探测出的阶跃)Fig.2 Continuous GPS time series of YANC station (The green is the normal point, the black is gross error, and the orange vertical line is the detected step)
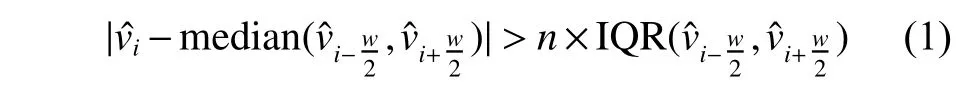
式中:vˆi为拟合后的残差,w为窗口大小,n是用于设置拒绝水平的整数因子,一般设置为3,median为中位数函数,IQR为四分位范围统计函数。
2.2 加权最小二乘估计速度及其精度
本文采用加权最小二乘进行GPS测站的速度及速度不确定性的计算,参数方程如式(2)所示。

式中:ti表示GPS坐标时间序列的单日解历元,以年为单位;a为测站起始年份第一天的测站位置(横轴截距);b为线性速度;c和d为年周期振幅;e和f为半年周期振幅;jk为由于各种原因引起的阶跃式突变;tjk为发生突变的历元;H为赫维赛德阶跃函数(Heaviside step function),当ti小于tjk时,H值为0,当ti大于或等于tjk时,H值为1;vi为测量误差。
假设参数矩阵x=[a b c d e f jk]T,GPS时间序列的观测方程为
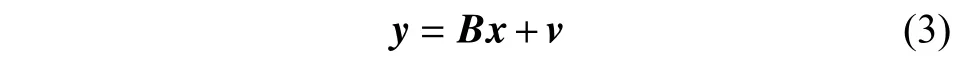
式中:y为单日解,B为系数矩阵,v为随机误差vi的矢量。利用加权最小二乘法(式(4))计算出每个测站的速度、年周期、半年周期及阶跃。
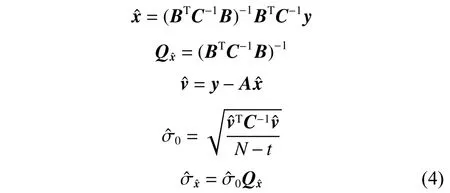
2.3 极大似然估计
采用极大似然估计方法选取最优的噪声模型协方差矩阵[17],见式(5)。

式中:ln为自然对数函数,lik为极大似然函数,det表示矩阵的行列式,是式(4)中所估计的最小二乘方残差,C是所选噪声模型的协方差矩阵,N为测站时间序列的历元个数。其中C由多个噪声模型组合而成,如式(6)所示。

式中:aw为白噪声振幅大小,I为单位阵,n为噪声组合个数,pi为其余噪声类型的振幅,Ji是不同噪声模型的协方差矩阵,所有的矩阵都为N×N的矩阵。其中,aw、pi为待估计参数。闪烁噪声的近似噪声模型J-1为

式中:n为行数;m为列数。
随机游走噪声的模型J-2为

式中:Δti=ti-t0。
幂律噪声的噪声模型J-3[18]可以表示为

其中T的转化矩阵为

式中:ΔT为时间间隔,φn可以表示为

式中:k为谱指数,将作为未知参数与一同估计。
2.4 频谱分析
本文利用Lomb-Scargle周期图法获得每个测站、每个方向残差噪声的功率谱图,该方法的优点是只对测量时间的时间序列数据进行评估,不需要连续的时间序列即可计算出功率谱。如式(12)所示。

式中:f为时间频率,t为式(2)中的单日解历元,yi为式(3)中的单日解,为其算术平均值,σ2为其方差,N为历元个数,常数τ 对应的是使周期图以任意的常数量独立于移位ti的时滞。由于本文中每个测站的时间序列都足够长,因此光谱指数的估计可以通过简单最小二乘拟合来实现。根据功率谱P和频率f,利用式(13)计算出谱指数K。

2.5 最优噪声模型评价原则
在极大似然估计中,不同的噪声模型会计算出不同的极大似然估计值,数值越大往往越可靠。但由于噪声模型参数的数量也会对模型的可靠性造成影响,因此,为了保证结果的可靠性,本文采用贝叶斯信息(Bayesian Information Criterion, BIC)准则[19]对不同模型的BIC值进行计算(见式(14)),依据BIC值最小的原则选取最优模型。

式中:H为参数个数,n为样本个数。
3 结果
3.1 光谱指数
本文在剔除GPS坐标时间序列中的粗差、趋势项、周期项、半周期项和阶跃后,得到GPS噪声时间序列。通过利用频谱分析法,估计了所有陆态连续站ENU 3个方向的功率谱。图3为KMIN站的功率谱图,由图3可以看出时间间隔大于14 d(即频率低于1/14)的噪声功率是恒定的,此时主要以白噪声为主[6],随着时间间隔的增加,噪声信号的相对功率明显上升。因此本文选取时间间隔高于14 d的数据进行简单的最小二乘拟合,图中以红色直线标出,直线的斜率为光谱指数。图4(a)为光谱指数估计的分布直方图。由图可知,东方向光谱指数的范围为-1.31~-0.48,北方向为-1.23~-0.55,垂直方向为-0.31~-1.244,不同方向上噪声光谱的特性没有明显差异。经计算,东、北、垂直方向的的加权平均数分别为-0.82,-0.84,-0.63,所有光谱指数的加权平均值为-0.76。已有研究表明[4],光谱指数是一个可以描述噪声源的指标,光谱指数的范围为-1<K<3,在-1<K<1中,K=0时,噪声源为白噪声,K=-1时为闪烁噪声,K=-2时为随机游走噪声。因而中国大陆GPS位置时间序列主要以白噪声和闪烁噪声为主。同时,从直方图4(a)可以看出,东、北方向频次峰值为-0.75,而垂直方向频次峰值为-0.5。本文认为造成该现象的原因是垂直方向的白噪声过大,掩盖了闪烁噪声的特性。图4(b)为光谱指数分布直方图。其中,东方向光谱指数的范围为-1.56~-0.58;北方向为-1.43~-0.70;垂直方向为-1.40~-0.48。它们的加权平均数为-1.02,-1.01,-0.83。从图4上看,各个方向没有明显的差异,垂直方向的光谱指数相对水平方向偏低,但光谱指数普遍在-1附近。上述两种结果表明:中国陆态连续站普遍具有闪烁噪声。同时,利用极大似然估计得到的光谱指数普遍比频谱分析的要小。在频谱分析中,光谱指数可能会被高估[20]。在本文中也验证了该结论。

图3 KMIN站功率谱图(红色为利用频率和功率谱值拟合的一条直线,它的斜率为谱指数)Fig.3 Power spectrum of the KMIN station (Red is a straight line fitted with frequency and power spectrum values, and its slope is the spectral index)

图4 不同方法所得出的光谱指数对比图Fig.4 Comparison chart of spectral indices obtained by different methods
3.2 速度不确定性分析
本文计算了792个GPS坐标时间序列,发现如果仅使用白噪声模型进行速度不确定性的估计,速度不确定性会被严重低估。图5为其中10个测站使用不同的噪声类型所估计的速度不确定性。从图上可以看出利用白噪声模型估计速度的不确定性均低于0.05 mm/a,在白噪声模型中加入闪烁噪声模型、随机游走噪声模型以及幂律噪声模型后,速度不确定性会扩大10倍以上。因此不同的噪声模型会对测站速度以及速度不确定性造成影响,选择合适的噪声模型尤为重要。本文选择了贝叶斯信息准则即式(13)计算每个模型的极大似然估计值,以此选取每个测站的最优噪声模型。图6给出根据贝叶斯信息准则选取的264个连续站共792个分量的最优噪声模型分布情况。整体而言,所有的噪声分量以WN+FN为主。在水平方向上,东方向和北方向WN+FN噪声模型分别高达87%和90%。而在垂直方向上,以WN+PL噪声模型为主,占比为59%。因此,CMONOC连续站主要以WN+FN噪声模型为主。这与田云峰等[7]、李昭等[8]认为中国大陆CMONOC连续站的噪声模型为白噪声加闪烁噪声的结果一致。本文利用计算出来的速度及其不确定性,绘制了中国大陆连续站的速度场(见图7),箭头表示速度,椭圆表示速度不确定性。由图7可得,部分点(TJWQ(117.130°E, 39.375°N,HETS(118.295°E, 39.736°N等)的不确定性远大于其他点,这是由于通过贝叶斯信息准则判断出这些点更加符合WN+FN+RW噪声模型,不确定性会被扩大。当测站的GPS时间序列具有随机游走噪声特性时,测站石墩的稳定性可能较弱[20]。因此根据速度不确定性的解算结果,这些测站石墩可能存在不稳定的情况。
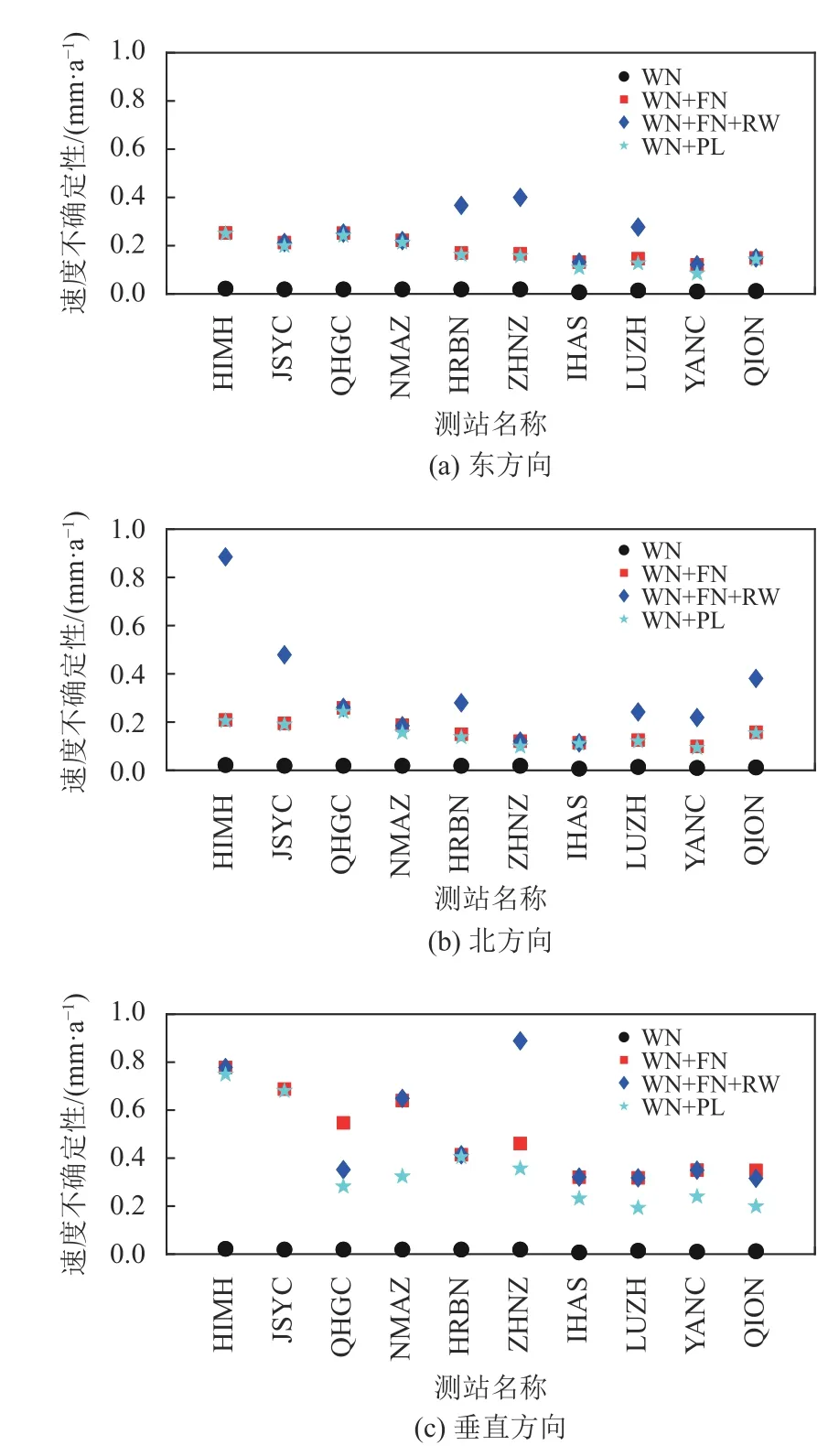
图5 不同噪声模型所得出的速度不确定性Fig.5 Velocity accuracy derived from different noise models
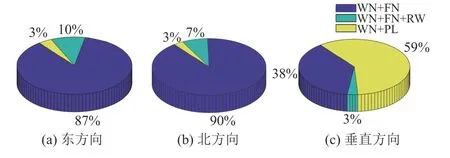
图 6 噪声模型不同分量占比Fig.6 Proportion of different components of noise model

图7 中国大陆连续站速度场及其速度不确定性Fig.7 Velocity field and velocity accuracy of continents in Chinese mainland
3.3 白噪声振幅大小与纬度关系
文献[20]利用23个全球连续站发现白噪声振幅在赤道上最大。因此,本文对空间范围纬度为15°~50°,经度为75°~135°区域的白噪声振幅进行空间分析。图8显示了东、北和垂直方向上白噪声振幅与站点纬度的关系图。图中各个方向的关系图存在个别离散点离拟合直线较远,这是由于部分GPS测站受外界因素影响(天线、接收机故障等)而白噪声增大。在图中能够看出垂直方向的白噪声振幅是水平方向上的2~3倍。另外3个方向的白噪声振幅都会随着纬度的下降而随之增大,这表明白噪声具有纬度依赖性。

图8 各个方向白噪声振幅与纬度关系图Fig.8 The relationship between white noise amplitude and latitude in all directions
4 讨论
本文对利用纯白噪声模型与最佳噪声模型所计算的速度不确定性进行了对比,最优噪声模型计算的速度不确定性是只使用白噪声模型的6~43倍。具体如表1所示。同时虽然利用最大似然估计的方法计算的速度不确定性是准确的,但计算效率较低。因此本文与在GLOBK软件中利用FOGMEx模型计算速度不确定性的方法也进行了比较。该软件通过缩放协方差矩阵的方式来近似估计速度不确定性[21],无需利用极大似然估计方法,具有速度快的特点。图9是白噪声模型、选取的最佳噪声模型和GLOBK软件利用FOGMEx模型所计算的速度及其不确定性对比图。在图9可看出东、北方向的白噪声模型所计算的速度不确定性均低于0.1 mm/a,垂直方向的速度不确定性少数在0.1~0.2 mm/a之间,利用最佳噪声模型所计算的速度不确定性比利用FOGMEx模型所计算的略大而垂直方向上具有明显差异。对于测站速度,在东、北方向上两种方法所计算的速度差异不大,94%的测站速度差值的绝对值小于0.2 mm/a,影响不大。在垂直方向中,可以看出利用本文的最佳噪声模型所计算的速度不确定性普遍高于利用FOGMEx模型所计算的速度不确定性,具有明显差异,并且22%的测站会存在速度差值过大的情况,具体差异如表1所示。根据表1可以看出在东、北方向上,速度及其速度不确定性的差异平均值都为0.1 mm/a左右,不具有明显差异。而垂直方向上,速度的不确定性差异平均值为(0.53±1.09) mm/a,具有明显差异。本文也对两者的计算结果统计了倍数关系,如表1所示,可以发现两者并不具有明显的倍数关系,不能利用简单的相乘系数来获取精确的速度不确定性。由此可以得出:对于毫米级地表形变和板块运动研究来说,在东、北方向上,两种方式所计算的速度不确定性不具有明显的倍数关系来获取准确的速度不确定性,但是两者方法的结果不具有明显差异,可以利用GLOBK软件中的FOGMEx模型较为快速地获取测站的速度不确定性。而垂直方向上两者存在差异,利用GLOBK软件无法获得准确的速度不确定性。
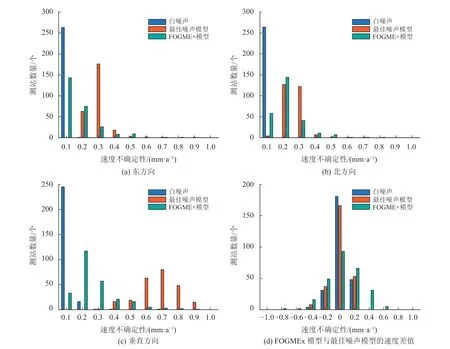
图9 WN、所选最佳噪声模型和FOGMEx模型速度以及速度不确定性对比Fig.9 Comparison of WN, Best Optimum Model and FOGMEx model velocities and velocity accuracy

表1 白噪声、最佳噪声模型与FOGMEx模型对比统计Table 1 The Optimum noise model is compared with the FOGMEx model
5 结论
本文利用频谱分析和极大似然估计的方法对CMONOC连续站的792个GPS坐标时间序列噪声特性进行了频谱分析。并且利用极大似然估计的方法估计并且判断出每个测站的噪声类型和速度不确定性。通过实验分析可以得出以下结论:
(1) 在频谱分析和极大似然估计方法中,频谱分析所计算出的光谱指数普遍要比极大似然估计方法得出来的光谱指数大。但两种结果均表明CMONOC连续站的噪声主要为白噪声和闪烁噪声。
(2) CMONOC连续站存在噪声多样性,并且不同方向上时间序列,其噪声类型也有所不用。其中WN+FN噪声模型占所有GPS坐标时间序列的73%。7%的GPS时间序列属于WN+FN+RW噪声模型,20%的GPS时间序列属于白噪声加幂律噪声模型。
(3) 通过噪声分析,发现有17个测站的随机游走噪声振幅偏大,极有可能是观测石墩不稳定造成的。
(4) CMONOC连续站GPS坐标时间序列的白噪声具有纬度依赖性,随着纬度的降低,白噪声振幅增大。
(5) 在东、北、垂直方向上,最优噪声模型计算的速度不确定性分别是只使用白噪声模型的(11.5±2.1)倍、(12.9±2.9)倍和(14.8±3.7)倍。利用极大似然估计方法与FOGMEx方法所计算的速度差距不大,利用极大似然估计方法所计算的速度不确定性分别是FOGMEx方法的(2.8±1.5)倍、(1.5±0.7)倍和(3.5±2.8)倍。

