季节指数改进的PM2.5质量浓度组合预测模型研究
曾江毅,李志生,欧耀春,金宇凯
(广东工业大学 土木与交通工程学院, 广东 广州 510006)
随着我国经济的快速发展,空气污染逐渐对人们的工作和生活造成严重影响[1],其中以雾霾为首的大气污染问题尤为突出,而PM2.5作为雾霾的主要成因之一,对人体造成各种程度的危害。PM2.5指的是在空气中当量直径小于等于2.5 μm的颗粒物,其来源十分广泛,包括化石燃料的燃烧、垃圾焚烧、工业粉尘、厨房烟气等[2-3]。近年来,有不少国内外学者运用了多种预测模型对PM2.5质量浓度进行了预测研究。张洪[4]结合风速、风向、气温、相对湿度等因素,Xu 等[5]还结合了道路信息,运用站点预测模型和网格预测模型对京津冀地区的PM2.5质量浓度进行了预测; Masood等[6]结合气象因素及大气污染物建立了支持向量机(Support Vector Machine)模型和人工神经网络模型,对印度德里的PM2.5质量浓度进行了预测;张怡文等[7]运用主成分分析法结合BP(Back Propagation)神经网络对合肥市的PM2.5质量浓度进行了预测分析,说明了PM2.5质量浓度受季节因素的影响较大,由于不同季节的气象有不同的特征,对PM2.5质量浓度的影响也不同; He等[8]和Asha[9]均运用了多元逐步回归,并分别结合其他方法,对上海市和印度马哈拉施特拉邦的PM2.5质量浓度进行了预测。
上述研究主要探究了PM2.5质量浓度与大气污染物、气象因子之间的相关性,并对PM2.5质量浓度进行了预测,结果显示大部分城市的PM2.5质量浓度均存在季节性变化规律。同时,文献[10-11]的结论也显示PM2.5质量浓度具有明显的季节变化趋势。针对这一现象,若能够对传统的预测模型进行改良,使其能够适应这种季节性变化规律,便可在一定程度上提高预测精度。广州作为广东省的省会、我国重要的中心城市,空气污染等环境问题备受关注,且广州地处亚热带季风气候区,气象因素具有明显季节性变化,具有广泛代表性。据广东省2021年第七次全国人口普查数据[12]显示,广州市常住人口位居全省第一,具有一定的研究意义。因此针对广州市的PM2.5质量浓度变化情况,本文将引入季节指数概念,改进传统的多元线性回归模型、多层感知器预测模型,建立一个改良的预测模型用于广州市PM2.5质量浓度的预测,为PM2.5质量浓度预测和防治工作提供一定的理论基础和改进思路。
1 数据来源及分析方法
1.1 数据来源
本文所使用的污染物数据来自于广州市生态环境局的实测数据(http://sthjj.gz.gov.cn/),原始数据为2015~2019年广州市PM2.5、PM10、NO2等污染物月数据;气象数据来自于中国气象数据网(http://data.cma.cn/),原始数据为2015~2019年广州市气温、湿度等月数据。
1.2 PM2.5季节性分析
PM2.5质量浓度会因为温度、湿度等因素呈现出一种周期性的变化。例如在夏季,降水可以在一定程度上清除大气污染物,而冬季降水相对较少,很难达到稀释大气污染物的效果。此外,风也可以在一定程度上减少大气污染物,风速越大越有利于大气污染物的稀释扩散[13]。分析广州市生态环境局以月为单位统计的PM2.5质量浓度的发展趋势,2015~2019年广州市PM2.5质量浓度的季节性变化规律如图1所示。
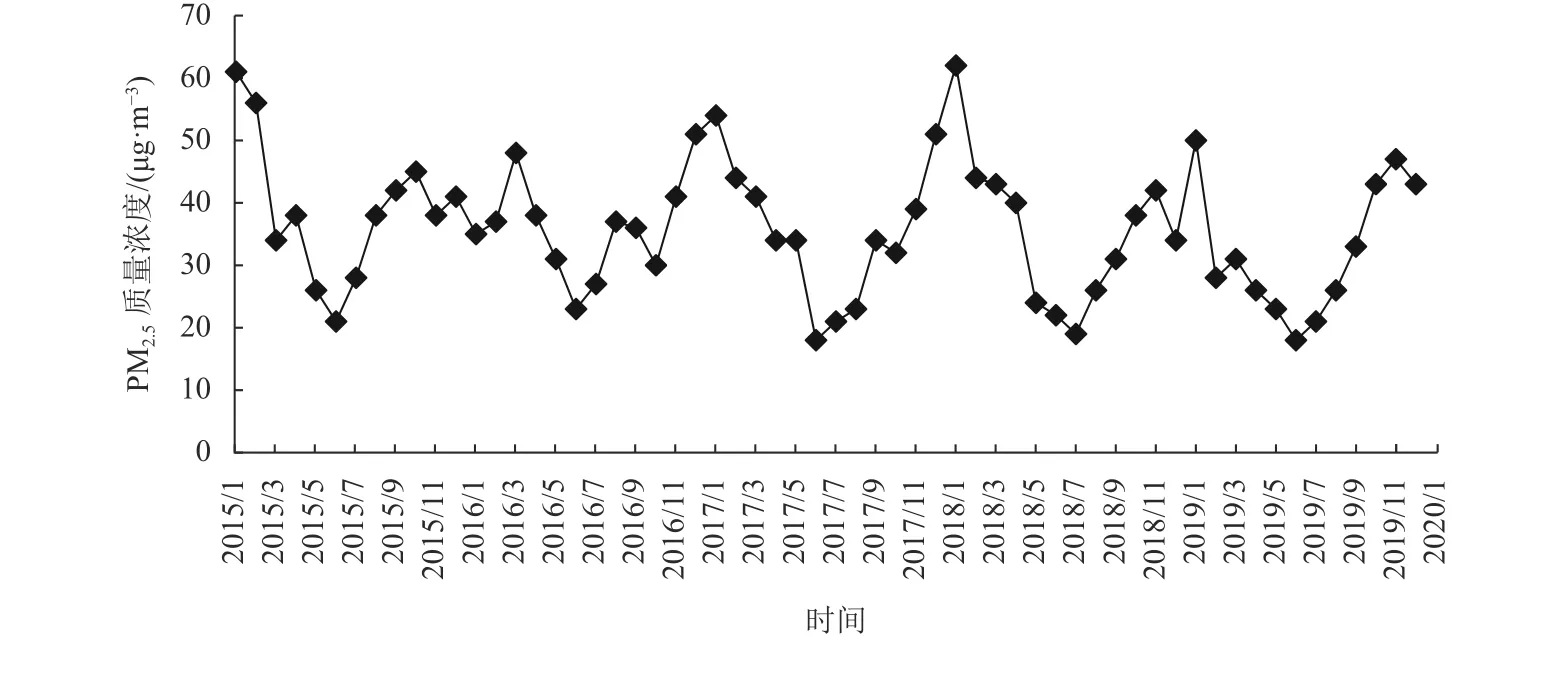
图1 2015~2019年广州市PM2.5质量浓度季节性变化规律图Fig.1 Seasonal variation pattern of PM2.5 concentration in Guangzhou from 2015 to 2019
其变化特征表现为以下几个方面:(1) 趋势下降性:据图1所示,在同一统计月,部分年份的PM2.5质量浓度有下降的趋势。主要原因是近年来广州市推进公交车电动化,也加大了城市扬尘的污染防控力度,城市大气颗粒污染物得到一定的控制。(2) 季节变化性:据图1所示,在同一年度,随着月份的变化,PM2.5质量浓度呈现出季节性变化。主要表现为4~8月,随着月降水量的增加,雨水可以更好地洗刷空气中的污染物,PM2.5质量浓度下降较快;6月PM2.5质量浓度最低。12月至次年1月气温达到最低,PM2.5质量浓度上升速率较快;大部分年份在1月出现高峰;PM2.5最高质量浓度约为最低的2~3倍。数据分析说明季节因素对于城市PM2.5质量浓度有一定的影响。
1.3 基于季节指数改进的多元线性回归和多层感知器模型
月度PM2.5质量浓度统计的时间跨度较长,容易受气候、假期等稳定因素的影响,大气中的PM2.5质量浓度呈现出一种非线性的下降趋势。
能够处理这种季节性波动的方法有3种,分别是小波分解、滑动平均法和惠普滤波分解。而惠普滤波分解是相对简单的方法,它通过有限的数据分解信号,不仅可以捕捉一般趋势,而且可以表征时间序列数据集中的季节因素。
1.3.1 季节指数
季节指数法既考虑了季节指数的趋势性变化,又充分利用了已知数据信息,因此广泛应用于能源、疾病等方面的预测[14-15],是一种较好的预测季节性波动时间序列的一般方法[16]。假设PM2.5的月质量浓度是由2部分组成,分别是趋势部分和周期性部分。其公式为
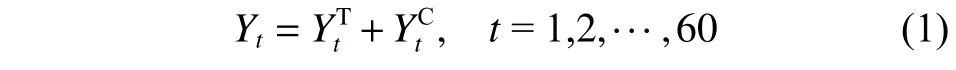
式中:Yt为第t个月的PM2.5质量浓度实际值;Y为第t个月的PM2.5质量浓度趋势值;Y为PM2.5质量浓度周期值。
由于该时间序列的趋势部分相对平滑,所以在使用惠普滤波器从初始的时间序列中分离趋势分量时,约束条件相当于式(2)的最小值问题。
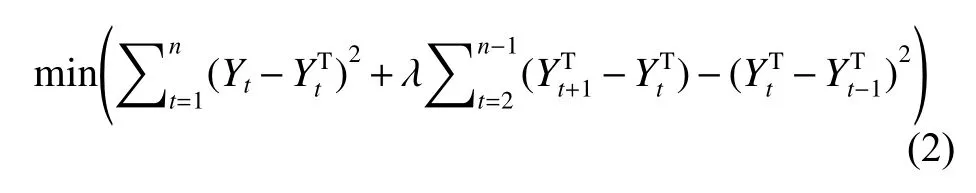
季节指数能够描述时间序列的季节性周期变化特征[18]。一般来说,季节因素对同一季节的影响相对稳定,因此季节指数可以通过计算每个月PM2.5质量浓度的实际值与趋势部分的比值得到。

式中:st为第t个月的季节指数;Yt为第t个月的PM2.5质量浓度实际值;Y为第t个月的PM2.5质量浓度趋势值。
1.3.2 多层感知器
多层感知器(Multilayer Perceptron ,MLP)包括输入层、输出层和多个隐藏层,是一种多层前馈人工神经网络。其结构简单,有良好的容错性、鲁棒性和极强的非线性映射能力[19]。人工神经元是MLP模型的信息处理节点,是MLP模型的最基本处理单元。神经元之间的连接强度称为连接权值,信息处理机制为
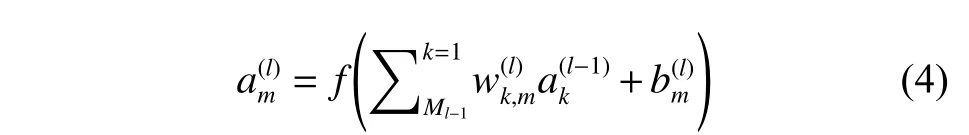
1.3.3 多元线性回归模型
线性回归是利用数理统计中的回归分析来确定2种或2种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。回归分析中包括2个或2个以上的自变量,且因变量和自变量之间是线性关系,该模型一般形式为
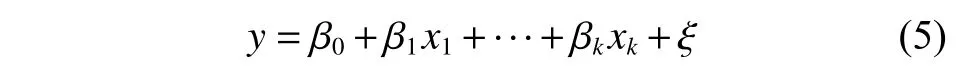
式中:y为因变量;x1···xk为 非随机变量;β0···βk为回归系数;ξ 为随机误差项。
2 实验结果与精度分析
2.1 数据处理
本文采用广州市2015~2019年的PM2.5月质量浓度数据,根据1.3.1部分,通过Eviews10进行惠普滤波分解,将原始的时间序列分成趋势部分与周期性部分。结果如图2所示。
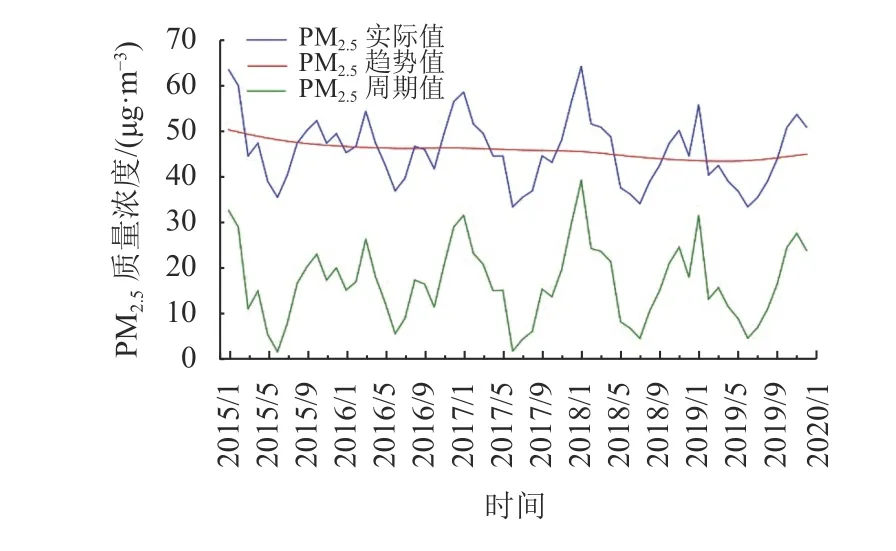
图2 2015~2019年广州市PM2.5质量浓度惠普滤波分解图Fig.2 HP filter decomposition diagram of PM2.5 concentration in Guangzhou from 2015 to 2019
如图2所示,广州市的PM2.5质量浓度具有缓慢下降的趋势,也存在明显的季节性波动,2017年表现的最为明显。通过式(3)对原始数据进行处理,即得到每个月份的季节指数。
2.2 预测模型构建
2.2.1 MLP模型构建
将PM2.5月质量浓度作为因变量,PM10、NO2、SO2、O3、CO、平均气温、平均风速、平均气压、平均相对湿度、雨天数(均为月度数据)作为协变量[20-22],且协变量均作正态化处理。构建的神经网络模型结构为9-16-16-1,即模型包括1个输入层、2个隐藏层和1个输出层。输入层有9个神经元,隐藏1层有16个神经元,隐藏2层有16个神经元,输出层有1个神经元。隐藏层的激活函数均为S型函数。模型的样本数和误差见表1。

表1 广州市PM2.5(趋势部分)神经网络预测模型情况Table 1 PM2.5 (trend part) neural network prediction model in Guangzhou
多层感知器神经网络会对自变量的重要性进行排序,结果显示“SO2”“平均相对湿度”“CO”重要性占比较高。其原因可能是PM2.5与SO2和CO具有同源性,均来源于城市机动车尾气。
2.2.2 多元线性回归分析
研究表明,PM2.5与PM10、NO2、SO2、O3、CO、平均气温、平均风速、平均气压、平均相对湿度、雨天数具有较好的相关性[23]。将2.1所求得的各月季节指数结合随机变量(广州市的PM10、NO2、SO2、O3、CO、平均气温、平均风速、平均气压、平均相对湿度、雨天数)计算各自的回归系数,得出回归方程为
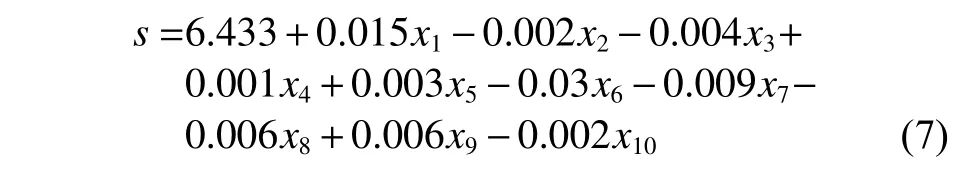
式中:s为季节指数;x1为 PM10质量浓度;x2为NO2质量浓度;x3为 SO2质量浓度;x4为 O3质量浓度;x5为CO质量浓度;x6为平均气温;x7为平均风速;x8为平均气压;x9为平均相对湿度;x10为雨天数。
2.3 实验结果
利用上述模型,可以得到各月的PM2.5质量浓度趋势值以及对应季节指数的预测值,将上文计算结果按照式(8)进行整合。

式中:Y0,t为 第t个月的预测值;s0,t为第t个月季节指数的预测值;Y为第t个月趋势部分的预测值。
整合后即可得出组合模型的预测值,组合模型预测值与实际值的变化曲线如图3所示。
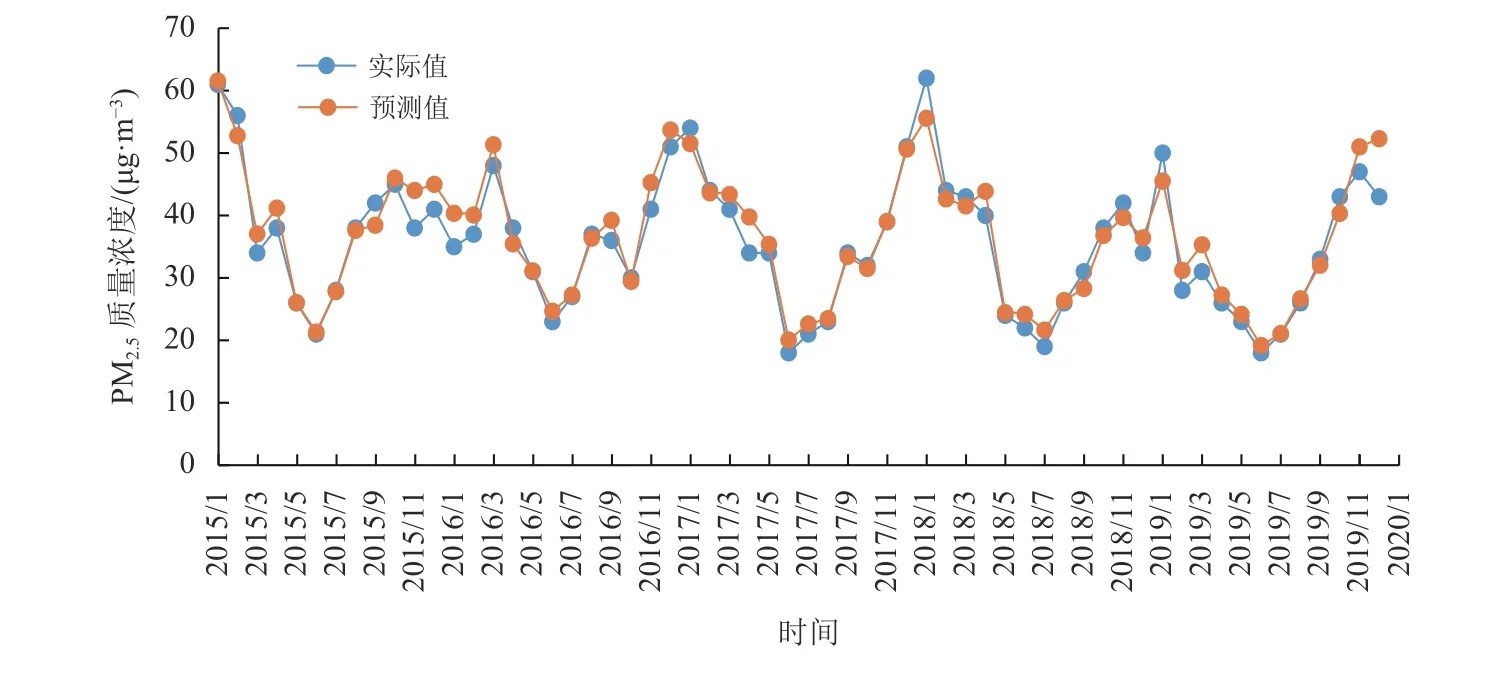
图3 广州市2015年~2019年PM2.5质量浓度组合模型预测值与实际值变化曲线Fig.3 Change curve between PM2.5 calculated value of combination model and actual value in Guangzhou from 2015 to 2019
2.4 精度分析
为验证模型的准确性,用3个指标检验模型的精度:均方根误差(Root Mean Square Error, RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、平均绝对误差(Mean Absolute Error, MAE)[24-25],见式(9)~(11)。

式中:e(i)=Yt-Y0为 误差;Yt为实际数据值;Y0为预测数据值。
为了验证本模型的性能,采用多层感知器与多元线性回归分别对原始数据进行一次计算(各模型参数与组合模型相同),多层感知器与多元线性回归模型的计算值与实际值的变化曲线对比如图4所示,各模型的预测精度如表2所示。

图4 广州市2015年~2019年PM2.5质量浓度其他模型计算值与实际值变化曲线Fig.4 Change curve between PM2.5 calculated value of other models and actual value in Guangzhou from 2015 to 2019
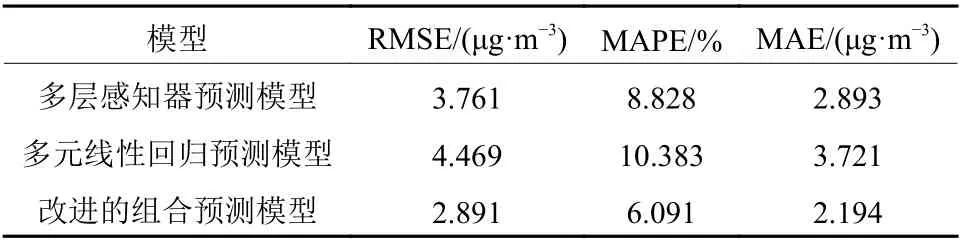
表2 各模型预测精度Table 2 Prediction accuracy of each model
由图3和图4可以看出,3个模型预测的结果和实际值总体来说符合情况较好,其中经过季节指数优化后的组合模型预测精度高于优化前的预测精度,根据表2中的3个指标可以看出,组合模型的RMSE、MAPE、MAE分别比多层感知器模型减少了23.1%、31%、24.2%;比多元线性回归模型减少了35.3%、41.3%、41%。
3 结语
本文根据PM2.5质量浓度具有明显的季节性变化这一特点,借助惠普滤波分解器,引入了季节指数,组合优化传统的多元线性回归模型和多层感知器模型,构建了基于季节指数改进的多元线性回归和多层感知器模型,以用于PM2.5质量浓度预测。实验结果表明,该模型精度均优于传统的多元线性回归模型和多层感知器模型。

