不同旋转雷诺数和内外半径比对泰勒库特流动特性的影响

王鹏亮，张晓威，金鼎铭，邱希望，刘国庆

（1.苏州欧拉透平机械有限公司，江苏苏州 215413；2.陕西柴油机重工有限公司技术中心，陕西兴平 713100）

0 引言

近年来，高速电机的研究和应用愈发广泛，相比传统电机，高速电机的电磁密度一般比较大，整体体积，转定子间隙比（指转定子间隙与转子直径的比值）比较小，使得转子的散热能力要求更高。在非防爆高速电机上，比较常见的做法是在转定子间隙内设置强制风冷（可能混有一定润滑油），从而解决转子散热问题。增大转定子间隙比，则风冷效果增强，但会降低电机效率；减小转定子间隙比，电机效率会增加，但转定子之间的气体流动、热场分布更加复杂。同时，电机转速的提高，不仅使得该气隙处摩擦损耗大幅增加，甚至会影响机组平稳运行。因此，对电机转定子间的气隙流动特性进行深入研究，掌握其影响因素和机理，为如何选取合理的转定子间隙比提供理论支持，十分必要。电机转定子之间的气隙流动，可以简化为2个相对旋转同轴圆柱的环形间隙流动，其关键是在环形间隙内出现的一种二次流动，即著名的泰勒漩涡，这是流体力学中的经典问题。随着转速的不断升高，环隙内流体流动现象会依次发生一系列的转换：层流库特（Couette）流→泰勒（Taylor）漩涡流→波动旋涡流→紊乱波动涡流→湍流［1］。电机转定子之间的气隙流动会同时耦合复杂的换热过程。

冯俊杰等［2］利用粒子成像速度场仪和数值模拟分别对泰勒库特（Taylor-Couette）流场进行测量，获得了各转速下涡流场信息，结果表明，各种特征存在一定的转速分段范围：当旋转雷诺数在100～350之间时，间隙内流场特征为层流涡特性；旋转雷诺数在350～2 000之间时，流场特征为波状涡特性；旋转雷诺数在2 000～3 000时，流场特征为调制波状涡特性；当旋转雷诺数大于3 000时，流场特征为湍流涡特性。何小英等［3］建立了基于圆柱坐标系网格的三维DSMC模型，对同轴旋转圆柱环隙内泰勒库特流中泰勒涡的形成进行了数值模拟，并分析了不同计算域和边界条件下稳定流场泰勒涡的轴向排列结构。王宇等［4］利用有限元方法，通过引入流函数将柱坐标下NS方程简化为流函数形式，减少求解变量，较详细地数值模拟了从层流过渡到泰勒涡流流动失稳出现分歧的全过程。韩晓婷等［5］对泰勒库特流动的研究中获得了泰勒涡的速度梯度、湍动能和有效能量耗散在环隙不同位置的幅值。蔡利亚等［6］对同轴圆柱间泰勒库特流进行模拟，发现了轴对称的旋转流动分歧现象，并展示了模拟结果。

前述工作均没有针对具体的气隙冷却问题，讨论不同雷诺数下的泰勒库特流动具体状态，以及恒定的旋转雷诺数下，不同的内外半径比对气隙流动状态的影响。由上可知，泰勒库特流的稳定性的研究方法主要有实验室模拟研究、理论分析和数值计算模拟等方法。基于此，本文对转定子之间的气隙流动特性进行了研究，采用数值模拟方法对冷却工质在电机转定子之间气隙内的泰勒库特流动进行模拟，获得气隙和转速变化下的涡流场信息，并对比分析不同条件下的涡形态，从而获得不同旋转雷诺数和内外半径比对泰勒库特流动特性的影响，以提升旋转机械性能和机器的长周期运行稳定性。

1 理论模型

1.1 物理模型

图1示出不可压缩流体在环形间隙中的流动模型。环形间隙由2个同心圆柱组成，内壁面的旋转角速度设为ω，外壁面为静止壁面。内外半径分别为R1和R2，轴向长度为L。

图1 计算所用三维立体模型Fig.1 The three-dimensional model used for calculation

1.2 网格划分

一般情况下网格越密计算精度越准确，然而网格数量越大相应的计算时间也越长，同时对计算机硬件要求也越高，因此进行合理的网格划分是取得正确计算结果的关键［7］，在进行数值计算时应根据实际的几何模型划分相应的理想的网格。整个过程关键步骤在于网格的划分，在研究不同雷诺数和不同内外半径比对泰勒库特流的影响时，由于几何模型为内外壁面均为光滑表面的环形区域，其几何结构相对简单，网格采用均匀分布，但是在讨论内壁面带凹槽结构时，必须对整个计算区域进行分块，分别对每一个块结构进行网格划分。

按照网格的生成方法，流动与传热问题数值计算的网格可以分成结构化网格和非结构化网格2大类。非结构化网格用于处理几何模型中的畸形点，为了保证整体网格的质量符合要求，其它部分虽然采用结构化网格但是网格在边界层处要进行加密。

本文中，结构化网格采用O-block来绘制，节点都采用均匀分布。

1.3 控制方程

控制方程即守恒定律的数学描述，任何流体运动都遵循三大基本定律：质量守恒定律、动量守恒定律和能量守恒定律，对应连续型方程、动量方程和能量方程。

1.4 条件设置

1.4.1 边界条件

内壁面：将壁面类型设置为Moving Wall，旋转轴选取z轴，旋转角速度根据不同旋转雷诺数设置。

外壁面：将壁面类型设置为Stationary Wall，Roughness Height设置为 0，Roughness Constant取 0.5。

进口边界条件：将壁面类型设置为velocityinlet，进口速度设置为 0.002 m/s，Turbulent Intensity设置为5%，Turbulent viscosity Ratio设置为10，其他保持默认值。

出口边界条件：将壁面类型设置为pressureoutlet，压力值设为0，保持和外界大气压一致，Backflow Turbulent Intensity同样设置为5%，Backflow Turbulent viscosity Ratio设置为10。

1.4.2 传热设置

首先，在计算模型中将耦合能量计算方程项［8］开启，由于探究的是温度梯度对泰勒库特流动的影响，所以在热边界条件（Thermal Conditions）选项中，分别指定内、外壁面的表面温度，又因为外壁面温度接近恒定，并通过试验手段测出大约80 ℃。所以保持外壁面等于80 ℃不变，通过改变旋转内壁面温度来控制温度梯度。

1.4.3 物性设置

本文采用的是空气和润滑油按不同比例混合形成的混合物，由于电机正常工作时，内部润滑油的温度接近80 ℃左右，所以润滑油的物性参数选取的是80 ℃润滑油的物性参数［9-12］，通过改变润滑油和空气的比例来使物性变化，进而研究物性变化对泰勒库特流动的速度涡和涡量分布的影响。

在Materials中添加空气air和润滑油lubricating oil 2种材料，由于FLUENT材料库中没有相关润滑油lubricating oil的物性参数，所以根据润滑油手册，将查到的物性添加到lubricating oil中，润滑油和空气两相混合物的计算模型选择Mixture模型。在phase1和phase2中分别添加air和lubricating oil 2种物质，并将模式调整到Mixture，同时可以根据需要调节不同的混合比。

2 不同旋转雷诺数模拟

2.1 数值设置

同心圆环尺寸设置为R1=45 mm，R2=50 mm，轴向长度L=200 mm，内外半径比η=0.9。计算所釆用的参数旋转雷诺数Re=ω R1d/v，其中v为运动黏度系数，网格数n、内壁面旋转角速度见表1。

表1 计算采用的具体参数Tab.1 The specific parameters used for calculation

2.2 结果分析

图2示出了旋转雷诺数分别为8 000，13 000，16 000，24 000的情况下间隙内流体的周向速度Uθ与径向位置的关系。其中径向位置通过Y*=（y-0.045）/0.005来进行无量纲化处理，在图2中可以看出，平均速度曲线没有表现出关于间隙中心的反对称性，这是和平板库特流动有明显区别的地方。随着雷诺数的增加，在内、外壁面附近的速度梯度增高，同时在流动核心区域角速度也随之增大。当雷诺数从8 000开始增大时，位于间隙中心区域流体的周向速度的值有显著的增长，增长了约200%。

图2 不同旋转雷诺数下的周向速度Fig.2 Peripheral velocity at different Reynolds numbers of rotation

图3示出取轴向中点处平面，环隙中流体沿径向方向不同位置处的X方向速度分布。

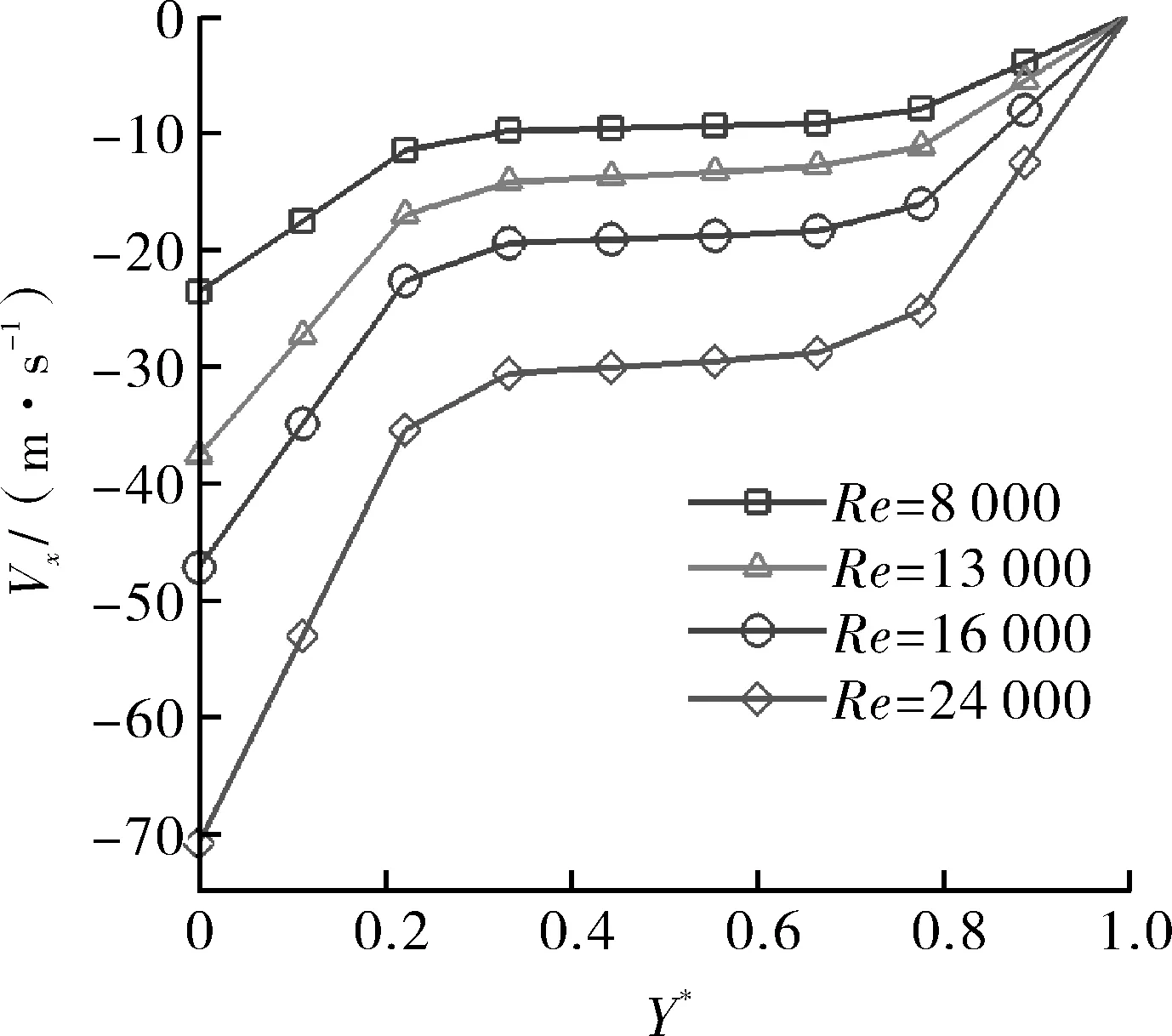
图3 不同旋转雷诺数下的X方向速度Fig.3 X-direction speed at different Reynolds numbers of rotation

从图中可以看出，从旋转内壁面处开始，沿着径向方向，X轴速度随着Y*增加而减小。对比不同旋转雷诺数下的速度曲线可以看出，随着旋转雷诺数的增加，沿X负方向速度大幅度增大，同时X方向速度曲线也没有表现出关于间隙中心的反对称性，靠近旋转内壁处的速度相对于靠近外壁面处减小得更快。最终由于外壁面是静止壁面，所以速度减小为0。

图4示出了旋转雷诺数Re分别为8 000，13 000，16 000，24 000时，环隙中流体在不同位置处的Y方向和Z方向速度分布。图5和6同理，从上到下依次是 Re=8 000，13 000，16 000，24 000的泰勒涡流场分布X轴和Z轴方向速度云图。从图可以看出，不同雷诺数下泰勒库特流的流场中涡量和速度的分布情况。以上3个图像都是截取的半个轴向长度的流场，同时也都对轴向和径向长度分别进行了无量纲化，其中Z*=z/0.005，Y*=（y-0.045）/0.005。

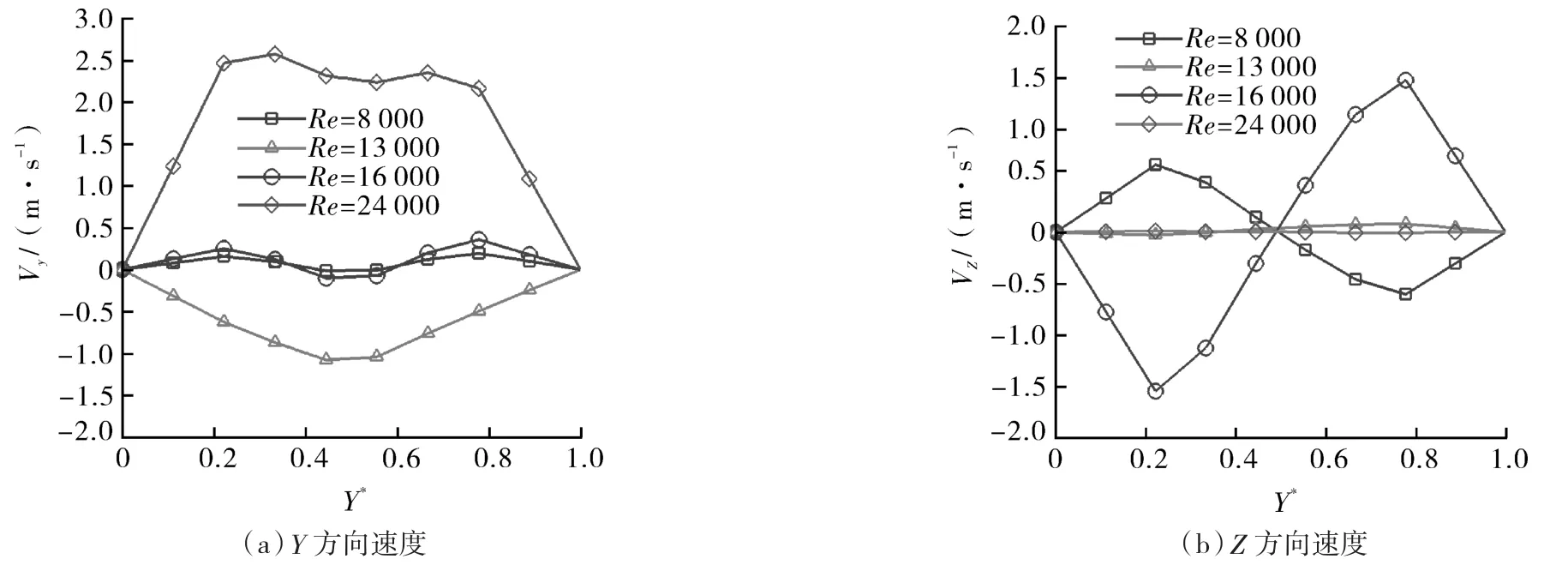
图4 不同旋转雷诺数下的Y和Z方向速度Fig.4 Velocity in Y and Z directions at different rotational Reynolds numbers

图5 不同旋转雷诺数下的泰勒涡流场分布Fig.5 Taylor vortex field distribution at different rotational Reynolds numbers

由图6可以看出，随着雷诺数的增加，速度旋涡变得越来越大，速度大小也随着增大，速度旋涡也变得越来越清晰。由图5可以看出，泰勒涡随着雷诺数的增加变得更加清晰，同时大小越来越规整，速度的大小也随着雷诺数的增加而变大。泰勒涡正负相间分布，大小基本一致，入口处由于是速度进口，导致旋转内壁面处附近的泰勒涡比较大。

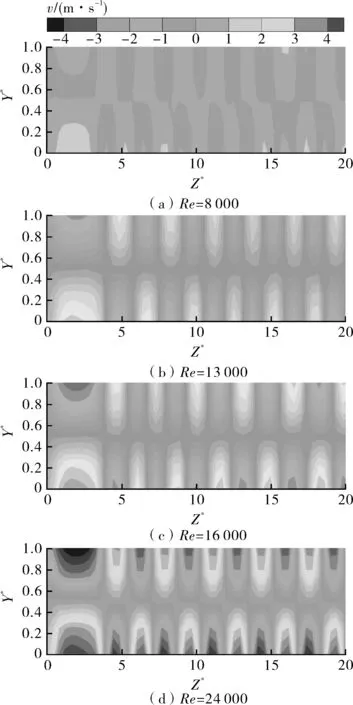
图6 不同旋转雷诺数下Z轴方向速度云图Fig.6 The nephogram of Z-axis velocity at different rotational Reynolds numbers

3 不同内外半径比模拟

3.1 数值设置

三维立体模型同图1类似，只改变环隙尺寸，其他条件保持不变。内壁面的旋转角速度设为ω，令ω=837.758保持恒定，即Re=13 000保持不变，外壁面为静止壁面。进口壁面设置为速度进口，并且流速设置为0.002 m/s，更改内壁面的半径值，保持外壁面半径值恒定不变，轴向长度L=200 mm不变，η=R1/ R2。算例一中，R1=45 mm，R2=50 mm，内外半径比η1=0.9；算例二中，R1=40 mm，R2=50 mm，内外半径比η2=0.8；算例三中，R1=35 mm，R2=50 mm，内外半径比η3=0.7；算例四中，R1=30 mm，R2=50 mm，内外半径比η4=0.6。具体计算方法同前节，所采用的具体参数见表2。

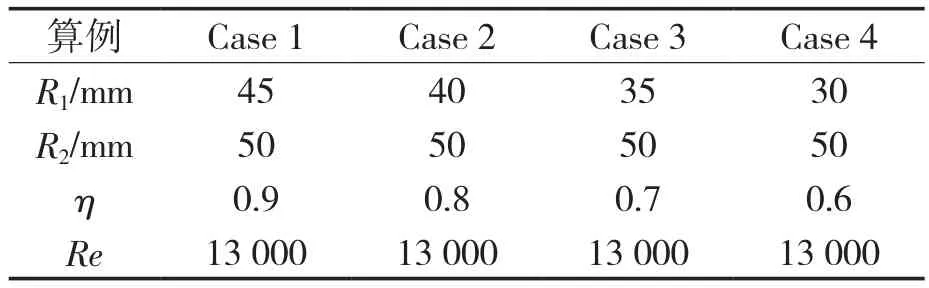
表2 计算采用的具体参数Tab.2 The specific parameters used for calculation

3.2 结果分析

图7 示出了半径比分别为 0.6，0.7，0.8，0.9 时流体的平均周向速度Vθ。在旋转圆筒和静止圆筒近壁区的平均周向速度Vθ曲线都已发展出明显的湍流边界层。随着半径比的增大，中心区域，即速度趋于稳定的区域，其速度值在不断增加，特别的是在靠近旋转壁面附近；随着半径比的增加，平均速度的梯度稍微减小。与此相反，在外壁面附近，平均速度梯度则逐渐增大。出现这种现象是由于半径比的增加，内外壁面的曲率逐渐趋于一致，外壁面附近沿周向剪切作用增强，而内壁面附近的剪切作用减弱，从而保证作用在内、外壁上的流体阻力和力矩达到平衡，这使得内外壁面附近平均周向速度分布的变化趋势不同。

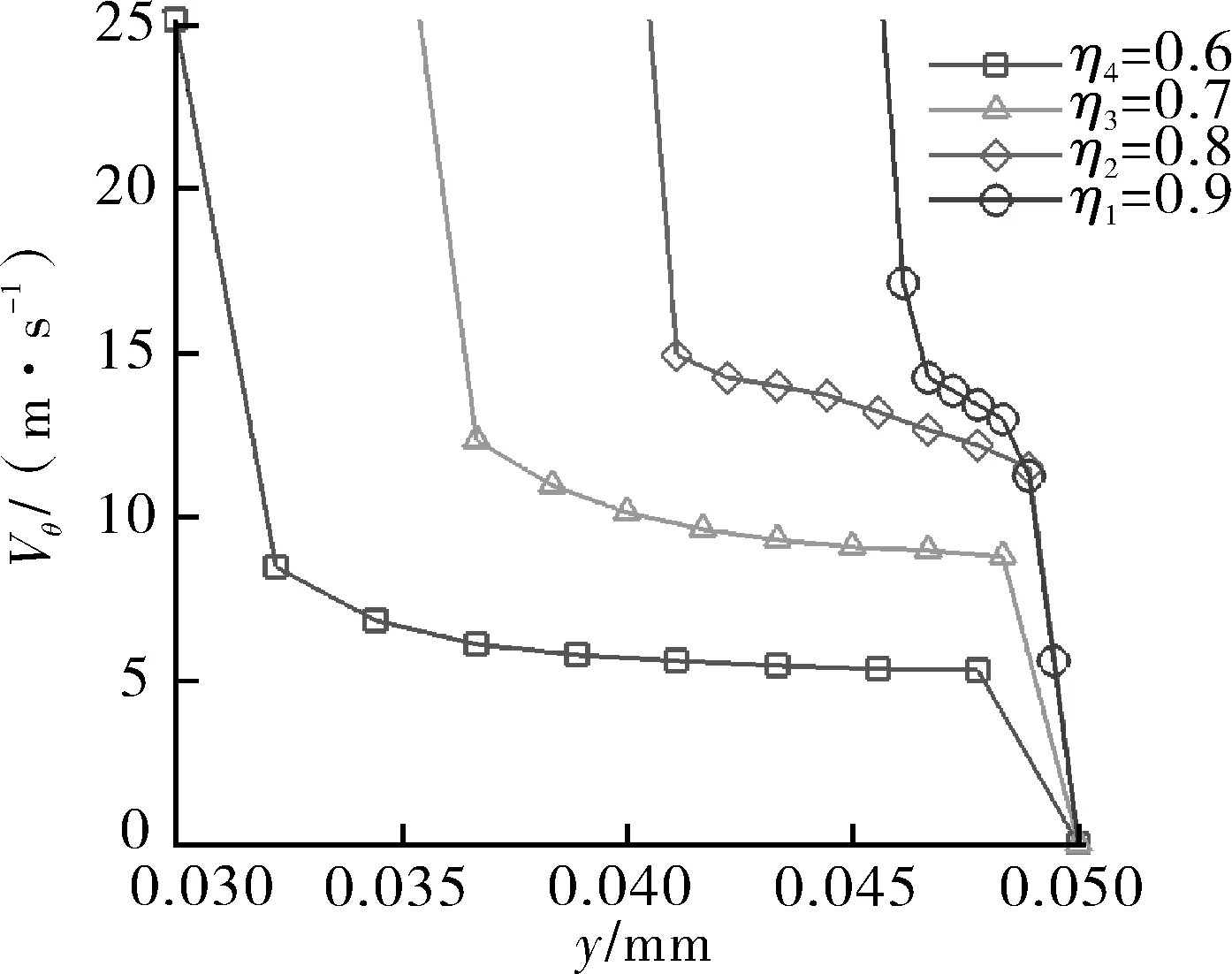
图7 不同内外半径比的周向速度随径向的变化曲线Fig.7 The variation curve of circumferential velocity with radial direction at different radius ratios

综上可以发现，随着半径比的不断增大，流体的流动特性更加趋近于剪切作用起主导的平板库特流动。

图 8，9 示出了内外半径比为 0.6，0.7，0.8，0.9的4个算例的流场涡量分布和速度分布。由不同半径比下的涡量分布图8可知，随着半径比的增大，旋涡的数量在增多。图中轴向方向截取的是模型的前1/2长度，当半径比0.6时，由于间隙太宽导致泰勒涡无法形成，半径比为0.7时才形成一对泰勒涡。

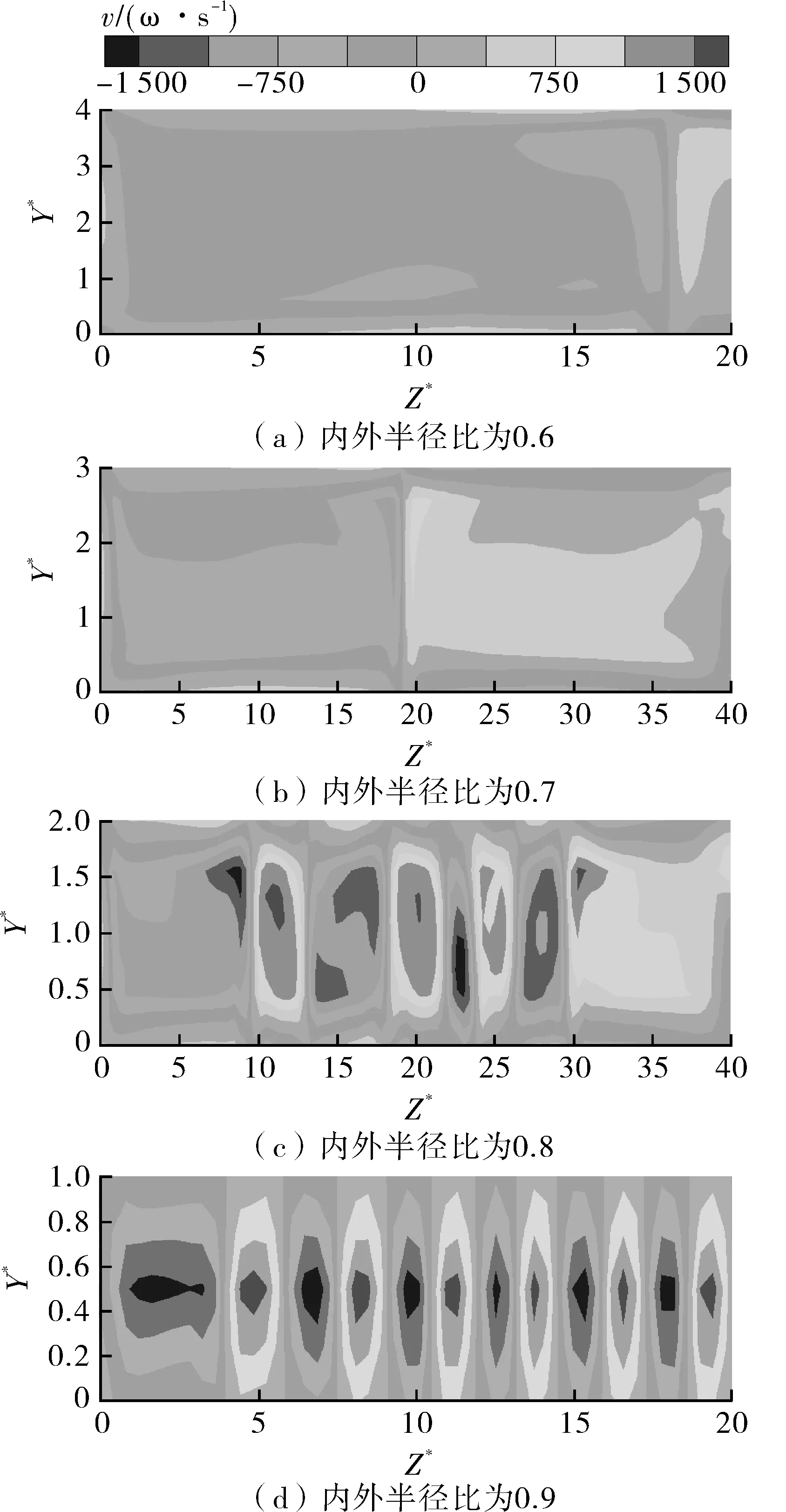
图8 不同内外半径比的X轴方向涡量分布Fig.8 Vorticity plots with different radius ratios along the X axis

由图9可知，在半径比为0.6的流场中，前一半只有正反一对旋涡，而在半径比为0.7的流场中，前一半就有正反2对，半径比为0.8时则有8对旋涡，半径比为0.9时甚至有12对，而且中间部分的每对旋涡的大小基本一致，只有两端的稍微大一些，这是由于速度进口和压力出口的壁面条件不同导致的。所以，随着半径比的增大，流场中旋涡的大小在逐渐减小，而旋涡的数量则大幅度增加。在轴向方向，位于两端的旋涡明显比中间区域的旋涡要大得多。

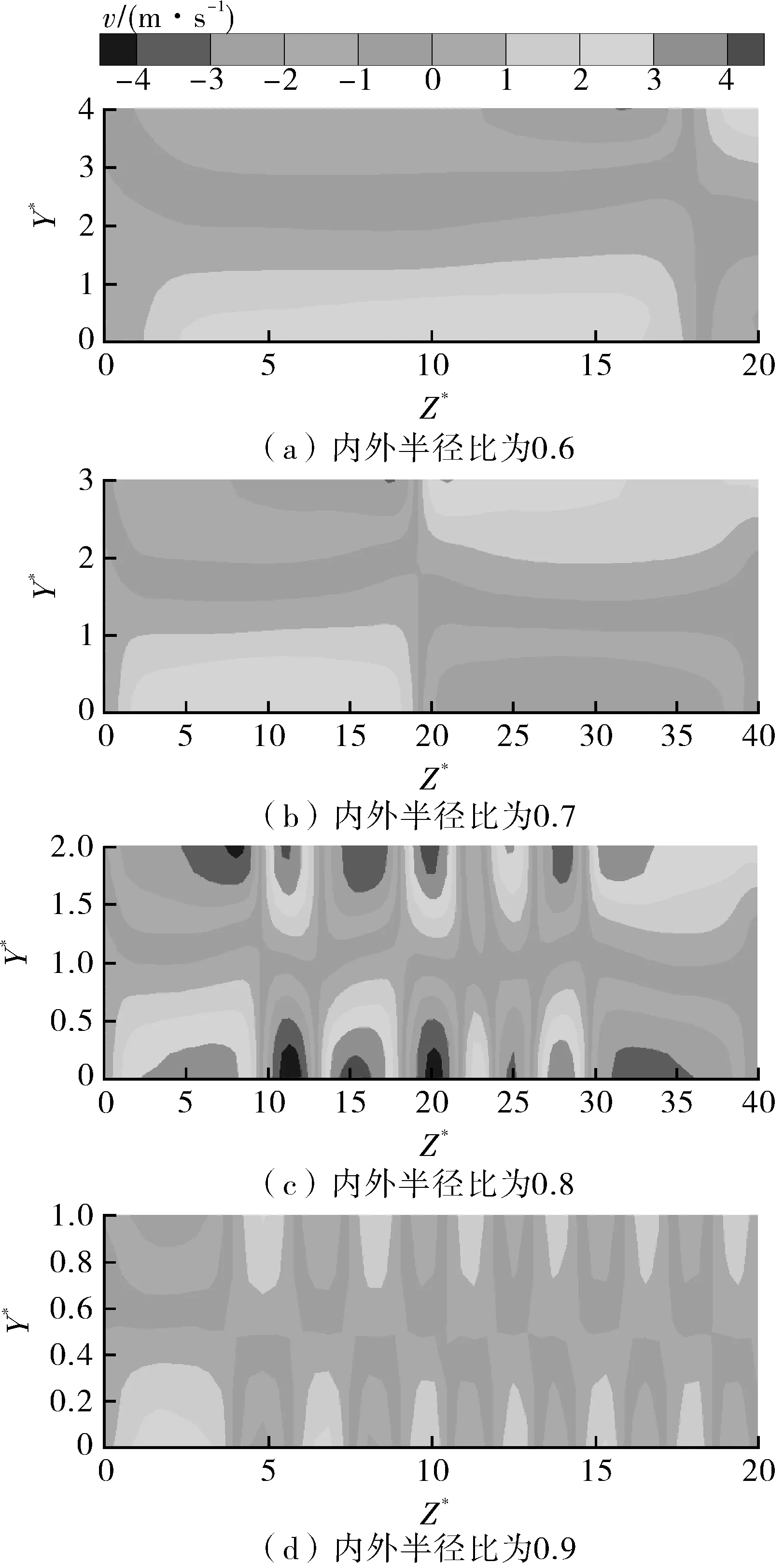
图9 不同内外半径的Z轴方向速度云图Fig.9 Nephogram of velocity with different radius along the Z axis

4 结论

（1）当雷诺数从8 000开始增大时，泰勒涡变得越来越清晰越来越大，当雷诺数增大到16 000以后，泰勒涡结构发生了严重的扭曲；内、外壁面附近的速度梯度增高，同时在流动核心区域的角速度也随之增大；位于间隙中心区域流体的周向速度有显著的增大；从旋转内壁面处开始，沿着径向方向，X轴速度随着Y*增加而减小。

（2）随着半径比的增大，中心区域的速度值在不断增加，特别是在靠近旋转壁面附近；平均速度的梯度稍微减小，与此相反，在外壁面附近，平均速度梯度则逐渐增大；旋涡的数量在增多，半径比为0.8时有8对旋涡，半径比为0.9时则有12对，而且中间部分的每对旋涡的大小基本一致，只有两端的稍微大一些；流体的流动特性更加趋近于剪切作用起主导的库特平板流动。