固液界面边界滑移对液滴振荡行为影响的VOF模拟
尹宗军,张椿英,苏 蓉,徐 辉,陈倩楠
(安徽信息工程学院 机械工程学院,安徽 芜湖 241100)
0 引言

流体力学表明,液滴润湿时流体和固体边界之间存在滑移运动.滑移运动意味着固液界面处的速度不连续性,而滑移长度λ是一个假设的边界内距离,在该距离处,固液界面处的流体速度达到固体边界速度.吴承伟等人[4]综述了液体流动的边界滑移及其相关问题的发展过程,探索了边界滑移的产生机理以及各因素对边界滑移的影响规律.近年来,相关文献表明粗糙壁面、微通道、外部气体环境、高压高剪切以及驱动压强差对边界滑移长度都具有较大影响[5-15].赵士林[16]认为滑移现象对超疏水表面材料的研究具有重要意义.秦长剑[17]采用耗散粒子动力学的方法,研究了微通道的边界条件及表面润湿性对边界滑移的影响.曹炳阳[18]研究了滑移现象对纳米尺度液体流动的影响规律及其机制.许少锋等人[19]研究了微通道疏水表面的滑移现象,模拟了平板间的Couette流动.他们的研究结果表明壁面与流体间排斥作用越强,即疏水性越强,壁面滑移越明显,并且滑移长度与接触角之间存在近似的二次函数关系.黄元丁[20]认为表面微观形貌对固体表面的润湿性和黏滞力有重要影响.他们着重探讨了表面微观形貌对边界滑移的影响,研究了五种状态的Cassie态表面上表面形貌、气液接触比、流道高度与驱动压强差对边界滑移长度的影响.
近年来,由于实验研究成本过高,数值仿真技术被大量运用到解决复杂流体问题中.VOF、CLSVOF(Coupled Level Set and Volume of Fluid)、相场动力学等方法分别被运用到液滴撞击领域中,模拟得到的结果与实验取得高度一致性.值得一提的是,模拟手段对改变撞击参数更为简单,且能给出液滴内部的动力学信息,例如压力、速度等,这将有利于某些流动现象的机理解释.然而,已有的研究多数是基于静态网格,也就是网格化后,网格不再变化,这不利于捕捉像液滴这样形变较大的流体.若要使用静态网格精确捕捉,就需要细化整个计算域,这不利于减少计算时间.动态自适应网格可以精确捕捉所设定的物理量的变化,在物理量变化剧烈的地方自动细化网格,而在物理量变化不剧烈的地方自动粗化网格加快计算.因此,当下迫切需要解决的技术问题是:(1)如何使用模拟计算取代实验仍然能获得精确的结果;(2)如何在模拟计算中用最少的网格精确获得界面形变,节约计算物理时间.采用VOF界面追踪方法捕捉相界面,利用动态网格自适应手段减少不必要的计算,且在相界面处自动加密,就为单液滴撞击平坦固体表面的模拟提供了可行的手段.因此,本文基于VOF界面追踪和自适应动态网格技术探究了液滴撞击壁面的振荡行为,进一步揭示固液界面边界滑移对液滴振荡特性的影响.
1 控制方程与参数设置
1.1 控制方程
在VOF模型中,不同的流体组分共用一套相体积分数方程,通过引进相体积分数这一变量,实现对每一个计算单元相界面的追踪.液滴撞击表面模型只涉及液滴及空气两种流体,假设二者之间为不可压缩、互不融合的层流运动,定义液相液滴为主相(ρL和μL用于表示液滴的密度和黏度,相分数设为c=1),气相空气为第二相(ρV和μV分别表示空气的物理特性,相分数设为c=0),而c介于0和1之间时代表两相界面区域;即可将两相流动等效为一种混合物(密度ρ和黏度μ).该混合物的密度ρ和黏度μ可以用体积分数变量c分别表示为ρ=cρL+(1-c)ρV,μ=cμL+(1-c)μV.针对两相流流体运动的特点,流动控制方程包括连续性方程,带表面张力的动量方程以及VOF相分数方程[21]:
▽·u=0,
(1)
(2)
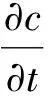
(3)
式中,u≡(u,v)为速度矢量,p为压强,D定义为Dij≡(∂iuj+∂jui)/2,g为重力加速度,δ为迪拉克算子,κ表示界面的平均曲率,n表示从液相流出的界面的单位法线.
1.2 离散方程
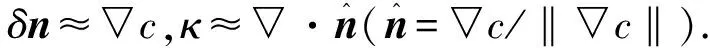
▽·un=0,
(4)
(5)
(6)
上述离散方程可进一步采用古典时间分解投影算法简化为[22]:
▽·un+1=0,
(7)
(8)
(9)
(10)
式中,ρi为密度,ui、μi、Di以及σi为对应时间节点i(i可取n、n+1/2和n+1)的值,u*表示辅助速度场.结合(7)式和(10)式,我们有以下Poisson方程:
调查结果显示,有7%的学生参加了3项以上的课题研究,28%的学生参与了1~2项的课题研究。硕士研究生参与课题研究对其科研水平的提升有很大的帮助,经常参与科研课题,能够激发学生的学习积极性和科研创新能力。
(11)
GERRIS软件是求解描述流体流动的偏微分方程的自由软件程序,其源代码是免费的.它具有以下主要特点:(1)求解含时不可压缩变密度Euler、Navier-Stokes方程;(2)自适应网格细化,分辨率根据流体的特征动态调整;(3)时间空间二阶离散精度;(4)可以灵活的附加源项;(5)支持MPI并行、动态负载平衡、并行脱机可视化;(6)精确的表面张力模型.基于GERRIS软件中成熟的VOF界面追踪技术以及自适应动态网格手段完全可以实现对单液滴撞击平坦固体表面的仿真模拟.(11)式使用GERRIS中的基于四元/八叉树的多级解算器求解该方程.同时,(8)式可以重新改写为
(12)
这是一个Helmholtz型方程,可以使用GERRIS中的多级Poisson解算器求解.
1.3 边界条件
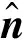
(13)

滑移边界条件和无滑移边界条件,这两种边界条件的法向流速都为零(即v=0),区别在于这两种边界切向速度u是否为零;即无滑移条件就是指在靠近壁面处流体的流动速度为零u=0,而有滑移条件就是它们之间有相对速度.滑移边界条件可以表示为
u=u0+λ∂u/∂y,
(14)
1.4 计算域与初始条件
首先在GERRIS软件中定义理想的计算域尺寸,液滴撞击壁面过程可以简化为一个Lx×Ly=2L×L二维计算域,L=8 mm,如图1(a)所示.计算域的右侧、左侧以及上侧边界指定为压力出口边界,底部指定为滑移边界条件.在计算域内部包含一个圆形区域(液滴,直径D0),液滴距离初始壁滴距离h=D0,以便液滴周围的气体流动能够在液滴撞击表面之前以物理方式发展,即保证将插入动量中的计算表面张力项始终具有最高的精确度.
液滴在铺展过程中液滴的形态是时变的,这就要求网格分辨率沿液滴/气体界面变化,因此动态自适应笛卡尔网格细化技术所用网格细化的判据可以表示为
‖c‖Δx/max‖u‖>δ,
(15)
式中,‖c‖是VOF体积分数变量c的值,Δx为子网格的尺寸,max‖u‖为流体穿过局部单元的最高速度,δ为阈值参量(δ取0.01).若(15)式满足,则GERRIS软件自动将网格细化一级.类似地,若满足下式
‖c‖Δx/max‖u‖<δ/4,
(16)
GERRIS软件自动将网格粗化一级,以减少计算.加密等级是指GERRIS软件中计算域是由一个个子正方形格子组成,若给定加密等级为10是指对构成计算的子正方形格子进行210=1024次切分,也就是说如果正方形格子边长为1 mm,则最小的网格长度为0.000 98.显然,加密等级越高,网格越密,计算精度越高,但物理计算时间也就越长.液滴界面局部区域内加密等级选择10;其余区域加密等级选择6,故相应的计算单元尺寸为L/210和L/26(即7.8125×10-3mm和1.25×10-1mm).初始的网格使用GERRIS软件生成.
初始时,压强p均设置为0,重力加速度g向下.如图1(b)所示,应用的数值网格的放大区域显示了移动的液滴以及网格的高分辨率,有助于更好地理解动态网格细化技术.图1(c)给出了液滴撞击过程中(i)碰撞、(ii)铺展以及(iii)反弹三种运动特征,表明网格能自适应地跟随液滴.
2 结果与分析
2.1 液滴撞击光滑固体表面的运动特征
我们将水滴(D0=2.0 mm,V0=0.31 m/s)与光滑固体超疏水表面(静态接触角θE=157°)的VOF模拟与文献[23]中的实验进行了比较.在计算中,水和空气的密度和黏度分别设定为ρL=9.98×102kg·m-3,ρV=1.2 kg·m-3;μL=1.003×10-3N·s·m-3,μV=1.8×10-5N·s·m-3,表面张力设置为γLV=7.5×10-2N·m-1.边界条件为自由滑移边界.
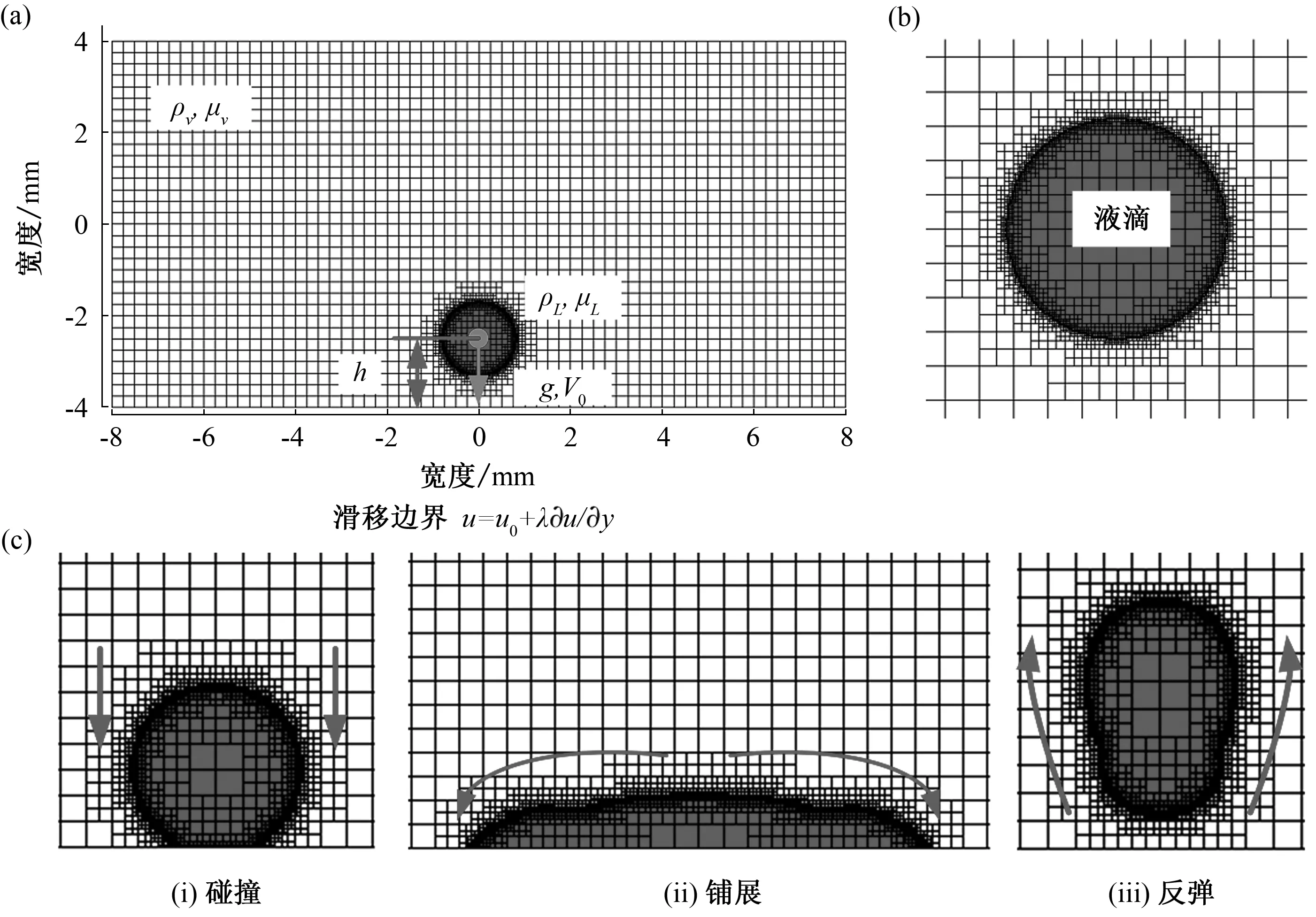
图1 液滴的滑移边界条件及运动特征

图2 液滴撞击光滑固体表面的运动演化
图2(a)和(b)所示分别为VOF模拟与文献[23]的液滴撞击光滑固体表面的运动演化图,图2(c)显示了铺展因子β的时间变化曲线(定义为β=L/D0,L为当前的润湿长度).当液滴接触壁面时,液滴底端流体开始向四周铺展.定义时间节点t=0.0 ms为水滴刚接触到固体表面时刻,此时β=0.大约1.6 ms后,液滴底部出现褶皱型,由于疏水表面的黏附力影响,液滴的下部并没有形成向四周的径向流动.随着液滴高度的降低,在t=3.8 ms时,液滴底部达到最大润湿面积,最大铺展因子βmax=1.85.在时间t=4.0 ms时,液滴呈现扁平状,液滴中出现向上的突出.这种行为的出现实际上与能量转换有关.当液滴撞击到固体基底上时,由于固体表面的阻挡,液滴的法向动量发生变化,液滴周向铺展以扩大表面积,直到动能完全转化为表面能量;这种不平衡状态是暂时的,在表面张力的作用下,液滴已经周向铺展的流体会向中心回缩,形成反向惯性力.在时间6.8 ms到10.8 ms内,这种反向惯性力迫使湿滴面积减小,β值不断减小.在t=11.2 ms时,这个反向惯性力迫使水滴从基板上反弹.图2(c)进一步表明液滴撞击光滑固体表面过程中模拟和实验的液滴铺展因子β变化具有一致性.
2.2 固液界面边界滑移对液滴振荡的影响
为了使我们的结论更具普遍性,我们使用了两组(V0=0.2 m/s,θE=70°和V0=0.4 m/s,θE=110°)来充分解释滑移长度λ对液滴振荡特性的影响.更具体地说,在VOF计算中我们使用了五种不同的边界条件:λ=0.005 mm、0.2 mm、0.4 mm、0.8 mm以及自由滑移边界.这里,选择直径D0=1.6 mm的水滴作为仿真模拟对象.
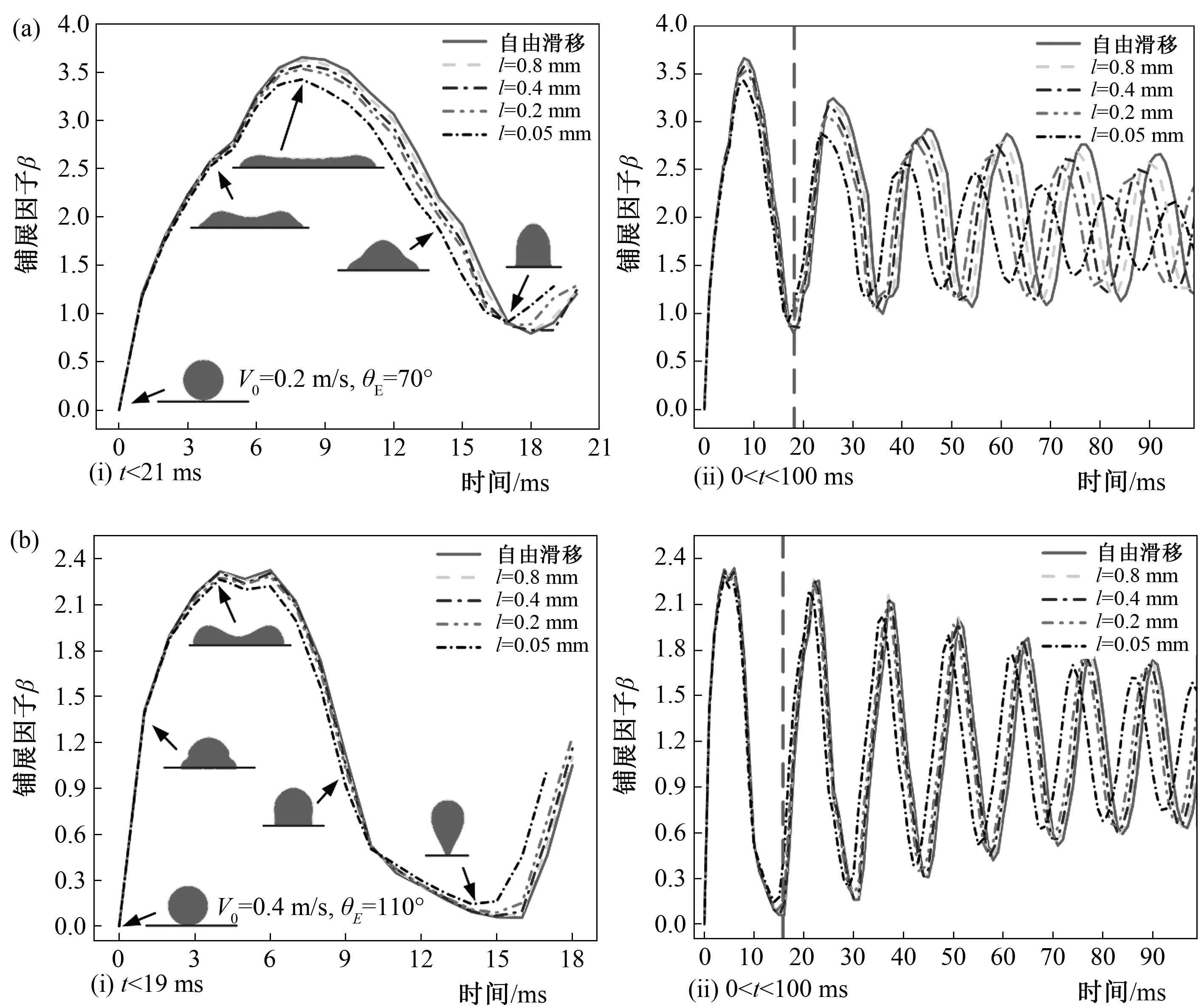
图3 不同滑移边界条件下铺展因子β的时间演化
图3显示了在不同滑移边界条件下,当V0=0.2 m/s,θE=70°(亲水表面,近毛细管铺展)和V0=0.4 m/s,θE=110°(疏水表面,近反弹)时,液滴在光滑表面上铺展因子β的时间演化图.图3左侧用于表示第一个振荡周期(i),这有利于描述液滴的最大铺展因子βmax;图3右侧用于表示100 ms内液滴的振荡行为(ii),这有利于描述液滴振荡行为的基本物理量,如平均振幅比χ以及平均振荡周期τ.在图3中,无论是近毛细扩散还是近反弹,都观察到了液滴振荡变化的类似曲线.可以看出,近毛细铺展比近反弹的振幅更大.图3(a)-(i)和图3(b)-(i)均表明,在第一个振荡周期下,铺展因子βmax的值略有变化.在第一个振荡周期后,边界滑移显著改变了液滴振荡的平均振幅比χ以及平均振荡周期τ,尤其是在组V0=0.2 m/s,θE=70°中(见图3(a)-(ii)).其原因是铺展长度较大时,较小的滑移长度导致了更多的能量损失.图3(a)-(ii)表明,当λ=0.05 mm变化到自由滑移边界条件时,平均振幅比χ和平均振荡周期τ分别为1.073/14.7 ms,1.066/15.7 ms,1.064/16.1 ms,1.056/16.7 ms和1.054/17.3 ms.λ=0.05 mm的χ值比自由滑移条件下的值小了2%,τ值减小了15%.这意味着随着λ值的减小,振荡阶段消失得更快.对于图3(b)-(ii),平均振幅比χ和平均振荡周期τ的值分别为1.074/13.7 ms,1.073/13.7 ms,1.066/14.1 ms,1.064/14.2 ms和1.063/14.2 ms.图3表明,边界滑移λ值越小,固液界面处的液体剪切速率越显著,这将更有效地抑制液滴振荡.
3 结论
当前的研究针对带有移动接触线的气液两相流动的数值研究,在固壁边界处引入滑移边界条件.通过GERRIS软件内部二阶精度的离散格式,利用成熟的VOF界面追踪技术以及自适应动态网格手段实现对液滴垂直撞击光滑表面进行了二维VOF模拟.本研究的主要目的在于探讨固液界面边界滑移对液滴振荡行为的影响.具体而言,是为了了解液滴撞击固体表面的振荡行为如何响应滑移边界的变化,并提供一些可行的策略来缩短一些潜在应用的振荡时间.研究结果表明在较低的滑移长度值下,如λ<0.05 mm,液滴在亲水表面上铺展,铺展因子β衰减变得更加明显.在滑移长度较高的情况下(包括自由滑移条件),如λ>0.2 mm,滑动长度的增加对亲水性或者疏水性表面上的铺展特性均影响不大.

