基于ANSYS Workbench的发动机曲轴有限元分析

白顺平，杨 振，陈国磊

(1.新疆天池能源有限责任公司，新疆 昌吉 831100;2.长城汽车有限公司，河北 保定 071000)

0 引言

曲轴通过将发动机曲柄连杆机构的动力转化成转矩并传递给发动机的其他部件，为汽车的运动提供动力，因此保证曲轴的正常工作对于保障发动机工况正常具有重要意义。本文针对某型号发动机的曲轴开展有限元分析，观测其工作能否满足发动机的正常使用要求[1]。

1 曲轴的建模

所研究对象为V12发动机曲轴，其主要尺寸参数如表1所示。

表1 曲轴的尺寸参数 mm

通过SolidWorks软件建立曲轴的三维模型，如图1所示。

图1 曲轴的三维模型

在建模过程中，对模型进行了一些简化，以保证有限元分析结果的正确，并减少计算时间，这些简化包括：

(1) 去除了有限元分析不需要的曲拐倒圆角结构。

(2) 曲轴为锻造曲轴，因此建模将其设计为一个整体结构。

(3) 只对影响曲轴受力分析的主要部件进行建模，省去了对曲轴力学性能影响不大的活塞连杆组等结构。

2 曲轴的有限元分析

有限元法通过将连续介质划分为网格单元节点，在单元节点之间作迭代分析进而得到整体结构的形变和应力分布，已经被广泛应用于线性结构材料的力学性能分析[2,3]。本文利用Workbench软件对曲轴开展静力学分析和模态分析，以保证曲轴的正常工作。

本曲轴采用的材料为42CrMoH，其物理以及力学属性为：密度ρ=7 850 kg/m3，弹性模量E=212 GPa，泊松比μ=0.28，屈服极限930 MPa。

2.1 曲轴有限元静力学分析

2.1.1 网格划分

利用自由划分网格方法对曲轴模型划分网格，得到的有限元模型如图2所示，共得到159 588个网格节点和96 439个网格单元。

图2 曲轴的有限元网格模型

2.1.2 载荷施加

在曲轴进行有限元静力学分析过程中，对曲轴左侧断面施加固定约束，然后施加载荷。已知曲轴在一个功冲程中最大扭矩为5 kN·mm，两处主轴颈的受力各为5 kN，大小相等，方向相反，这些载荷来自于与轴径连接的连杆。将轴径受力简化为集中载荷施加在轴径处，受力及约束情况如图3所示。

图3 曲轴的载荷施加

2.1.3 结果分析

经过求解，得到曲轴的应力和应变分布云图，分别如图4和图5所示。

从图4中可以看出，最大应力值发生在主轴颈以及连杆轴颈的过渡圆角处，且其值为642.73 MPa；从图5可知，曲轴的最大应变约为0.003，分布位置在第一、第二曲柄处；曲轴其余部位的应变量与应力值均小于此处。根据已知的曲轴材料参数，应力值小于其屈服极限930 MPa，表明曲轴结构满足强度要求，使用安全性较高，满足设计要求。

图4 曲轴的应力云图

图5 曲轴的应变云图

2.2 曲轴模态分析

曲轴在工作过程中高速转动，转速为2 500 r/min，约为40.81 Hz。当转速与曲轴的固有频率相近时，结构可能会发生共振，产生疲劳破坏。因此为了保证曲轴的正常工作，对曲轴进行模态分析，以保证曲轴在转动过程中不会产生共振现象。

2.2.1 曲轴的自由模态分析

对曲轴在Modal模块中进行自由模态分析，得到曲轴的前10阶模态振型，如图6所示，对应的固有频率及最大变形见表2。

图6 曲轴的自由模态前10阶振型

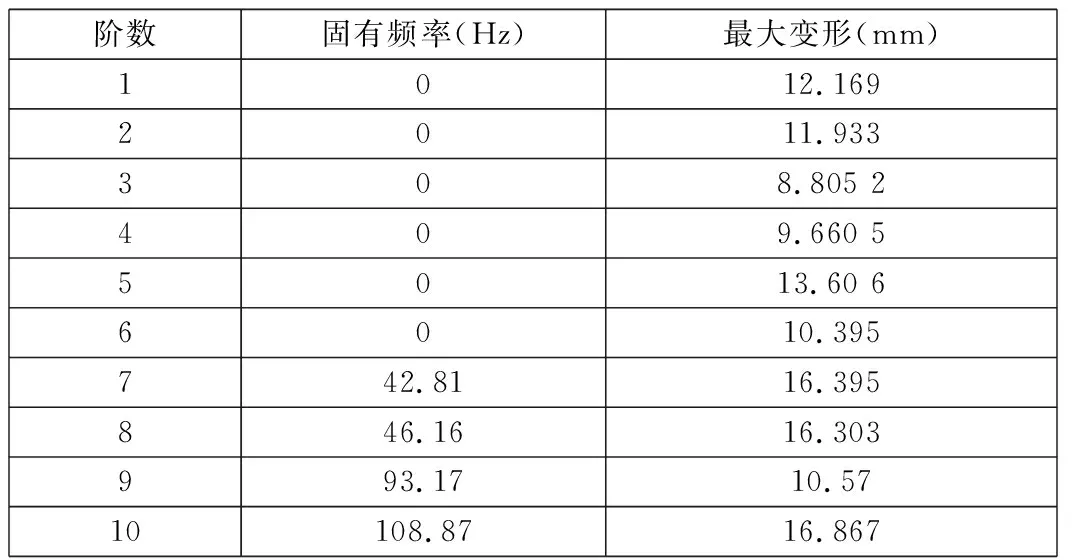
表2 曲轴各阶模态的固有频率及最大变形

在自由约束条件下，曲轴前6阶模态的固有频率很小，几乎可以忽略不计。但是第7阶固有频率与曲轴的工作频率较为接近，因此存在一定共振危险，所以需要进一步开展约束工况下的曲轴模态分析。

2.2.2 曲轴的约束模态分析

对曲轴进行附加约束条件下的模态分析，求得其前10阶振型，如图7所示，对应的固有频率及最大变形如表3所示。

图7 曲轴的约束模态前10阶振型

表3 曲轴约束模态的固有频率及最大变形

通过对曲轴约束工况下的模态分析可知，曲轴的各阶固有频率均远离曲轴的工作频率，因此以约束模态为准，认为曲轴在使用过程中不会因为工作状况产生长时间共振而发生破坏。

3 结论

通过对曲轴开展静力学分析和动力力模态分析可知，曲轴的最大应变为0.003，最大应力值为642.73 MPa，满足曲轴工作的静强度要求。同时约束模态分析显示，曲轴在正常工作过程中不会产生共振破坏，因此认为曲轴可以正常使用。