基于贝叶斯估计法的矿区地表沉降预测组合模型*

吴伟强，王卫红，訾应昆，耿诗画，冉茂莹

(1.西南科技大学 环境与资源学院，四川 绵阳 621010；2.国家遥感中心绵阳科技城分部，四川 绵阳 621010)

0 引言

甘肃金昌是我国最大的镍生产基地，镍矿资源占全国总储量的62%，被誉为“中国镍都”[1]。2016年至今，持续的地下开采导致金昌龙首矿西二采区采场塌陷并引发地面沉降。为确保矿区生产安全及最大限度地回采剩余镍矿资源，对矿区地表沉降开展预测研究具有重要意义。

矿区地表沉降机理复杂且影响因素众多，但仍具有一定的趋势性。差分整合移动平均自回归(Autoregressive Integrated Moving Average, ARIMA)模型在应对具有趋势性的问题时具有较好的表现[2]，径向基函数神经网络模型因能够逼近任意非线性函数而可以应对多影响因素和非线性问题[3]。但是单一模型的精度很难满足当前的矿区地表沉降预测需求，将单一预测模型进行组合，发挥各模型的优势来提高预测精度是未来沉降预测领域的发展趋势[4-8]。本文基于贝叶斯估计法，将ARIMA模型和径向基函数神经网络模型进行组合，通过将组合模型与单一模型和残差修正组合模型进行对比，验证该模型的综合性能，以期为矿山地表沉降预测提供另一种有效方法。

1 建立预测模型

为了验证本文提出的基于贝叶斯估计法的组合预测模型在矿区沉降预测中的优势，共采用4种模型进行预测对比。首先采用ARIMA模型和径向基函数神经网络模型进行单一模型预测，再将两种单一模型分别采用残差修正法和贝叶斯估计法进行组合模型预测。

1.1 单一预测模型

1.1.1 ARIMA模型

ARIMA模型是针对时间序列预测的常见模型。ARIMA(p,d,q)模型可表示为

(1)

式中：φi为自相关系数；Xt为当前项；θi为偏自相关系数；εt为噪声项；p为自回归阶数；q为移动平均阶数；L是滞后算子；d为差分阶数，d∈Z，d>0，而当d=0时，ARIMA模型等同于ARMA模型(即平稳时间序列模型)[9]。本文通过计算得出的最适合研究区沉降数据的参数值为：p=5，q=5，d=0。

指数平滑预测法是以本期历史监测数据为基础，引入平滑系数，以求得平均数的一种时间序列预测法，其计算式为

(2)

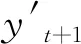
1.1.2 径向基函数神经网络模型

1988年LOWE和BROOMHEAD提出将径向基函数引入神经网络中。径向基函数神经网络因具有结构简单、收敛速度快、能够逼近任意非线性函数等优势而得到了广泛应用[10-12]。径向基函数神经网络是由三层构成的前向网络,其模型可以表示为

(3)

本文拟采用的网络结构如图1所示。

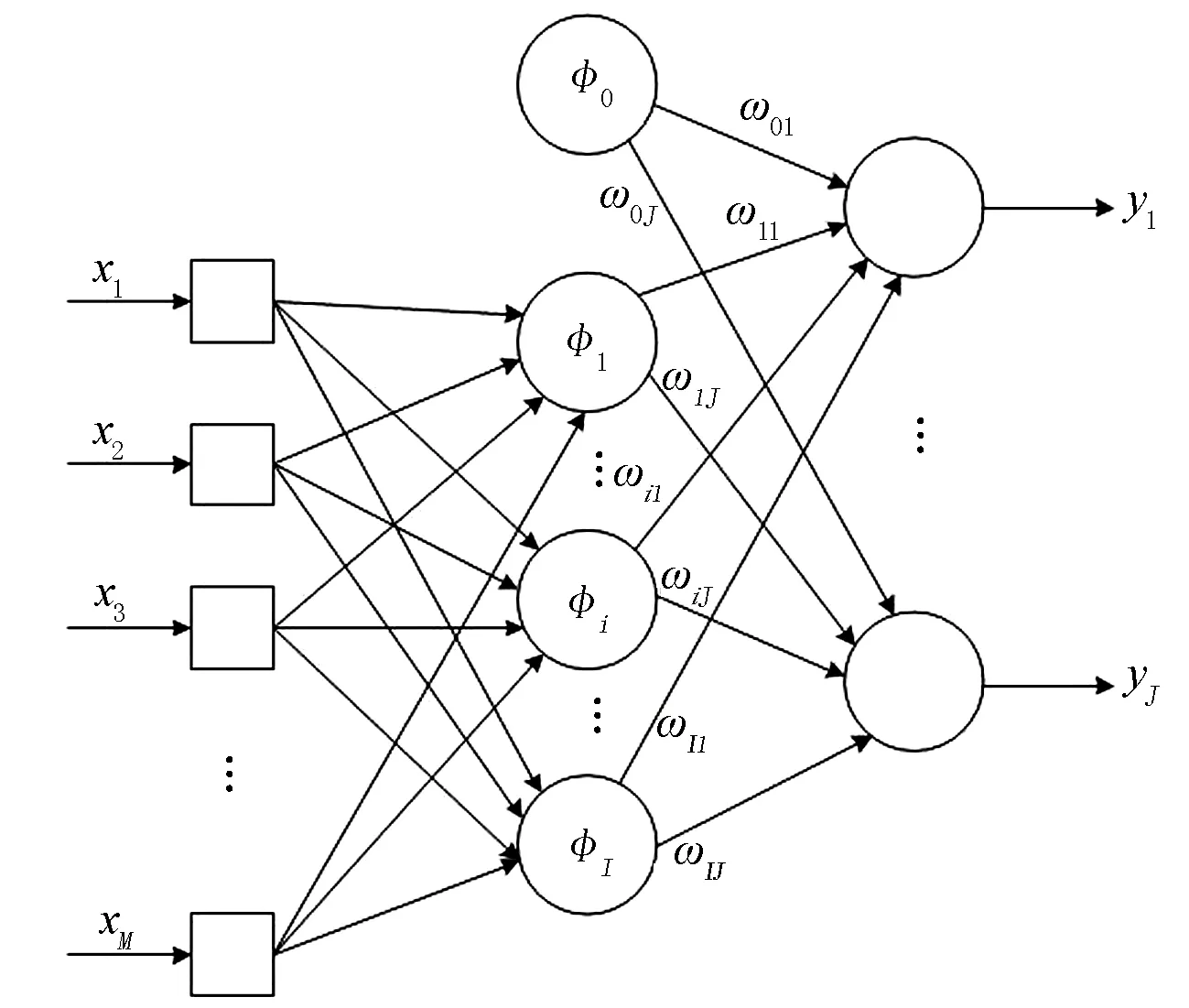
图1 径向基函数神经网络结构

网络学习策略采用随机选取固定中心，传递函数采用高斯函数：

(4)

式中，δi为频带系数。

在随机选取固定中心的方法中，唯一需要训练的参数是隐含层与输出层之间的权值，其步骤叙述如下。

1)选取基函数的标准差

(5)

式中，dmax为所选中心之间的最大距离，n为隐含节点的个数。

2)确定中心和标准差后，得到基函数

i=1,2,…,n。

(6)

3)采用伪逆法，输出权值矩阵ω

ω=G+d，

(7)

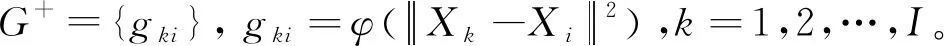
1.2 组合模型

1.2.1 残差修正组合模型

矿区沉降时间序列具有趋势性与随机性的特征，故采用ARIMA模型提取序列中的趋势性，采用径向基函数神经网络模型提取序列中的随机性。具体步骤如下：

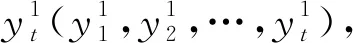
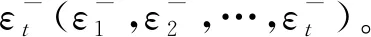
根据以上步骤求得残差修正组合模型的最终预测结果：

(8)

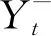
1.2.2 贝叶斯估计法组合模型

贝叶斯估计法根据多个不同基本模型当前时刻之前的预测表现对各个模型动态赋权[13-14]。本文将ARIMA模型与径向基函数神经网络模型作为基本模型进行组合，某一特定点的沉降量序列可由n个基本预测模型中任意一个模型来描述产生，即

(9)

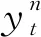
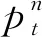
(10)

根据贝叶斯定理可知

(11)

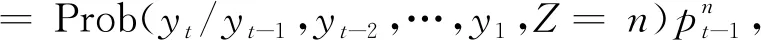
(12)

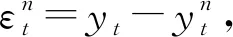
Prob(yt/yt-1,…,y1,Z=n)

(13)

合并式(12)和式(13)得

(14)

总结第t+1时刻的预测结果，用N个预测模型的预测结果组合表示为

(15)

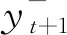
2 实验与结果分析

2.1 研究区概况

本文以甘肃省金昌市的金川硫化铜镍矿龙首矿西二采区为研究对象(简称“西二采”)。西二采矿区地势较平坦，平均海拔在1 500～1 800 m。地表无水系，属温带大陆性气候。由于持续的地下开采，西二采地表塌陷、裂缝明显，形成了巨大的安全隐患。目前沉降区面积约1.1 km2，其位置如图2所示。

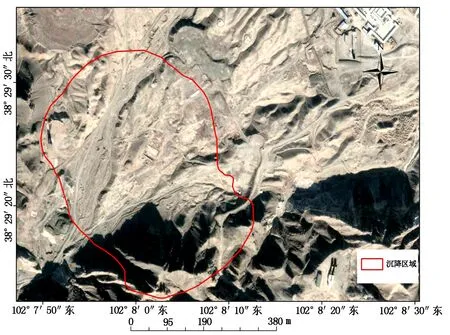
图2 沉降区位置

2.2 矿区SBAS-InSAR监测及分析

本文选取2019年3月22日至2020年6月8日共38个时相的Sentinel-1A卫星C波段升轨斜距单视复数(SLC)SAR影像(相邻两个时相的时间间隔为12 d)，采用SARscape5.2.1软件进行SBAS数据处理，提取了37期地表沉降信息。累积沉降值见图3。

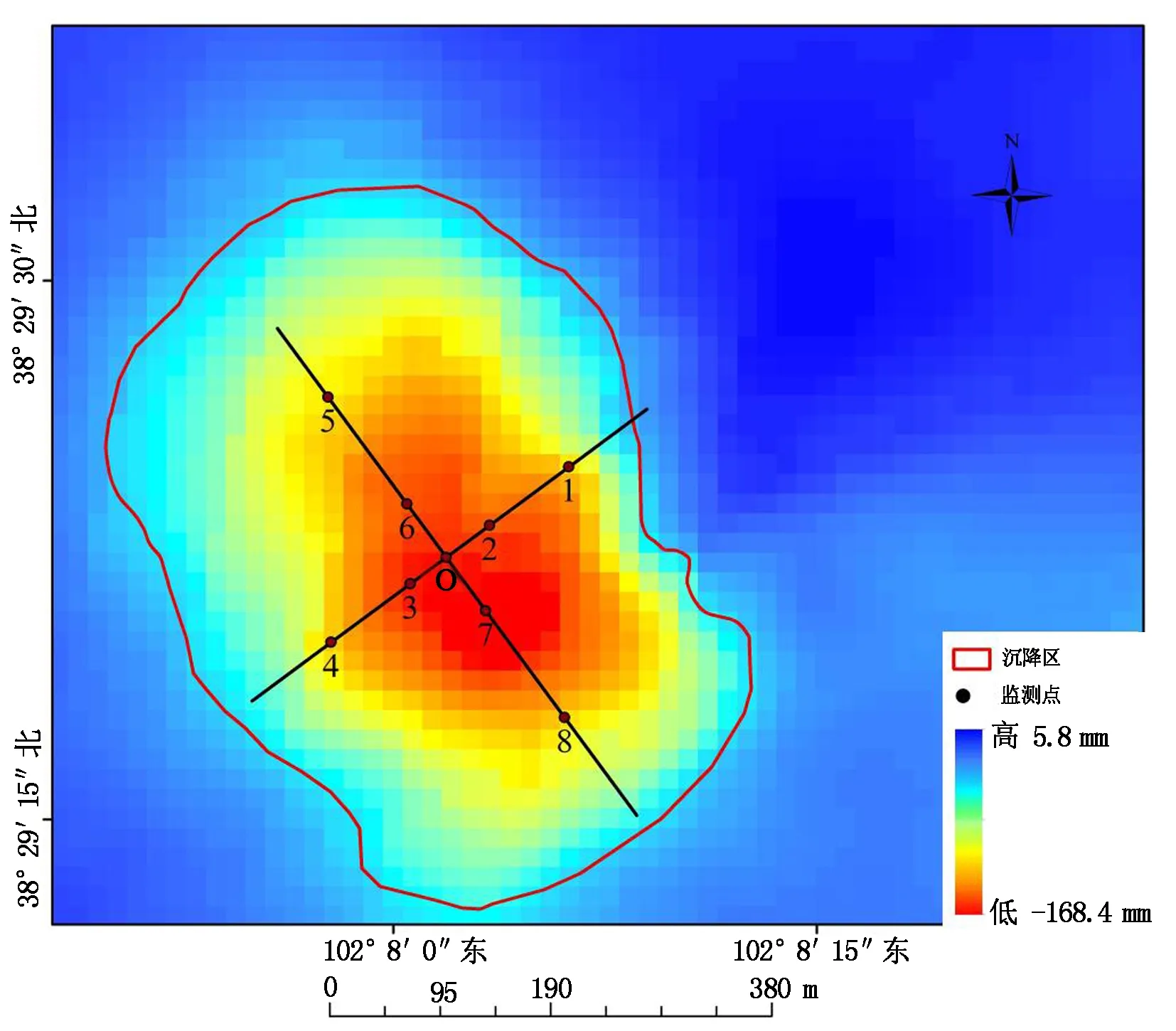
图3 累积沉降值

由图3可以看出，矿区沉降区域大致呈椭圆形，矿区在监测时间内最大累积沉降量达-168.4 mm。本文以最大累积沉降点sample O作为坐标原点，分别以椭圆形沉降区的短轴和长轴为横向和纵向，各选取4个样本点(sample 1-sample 4、sample 5-sample 8)，包括原点在内共9个样本点。

各样本点沉降变化曲线如图4所示。由图4可知，各样本点的累积沉降值以及沉降趋势相差不大，均在第1-第15期沉降较慢，第16-第37期沉降较快。

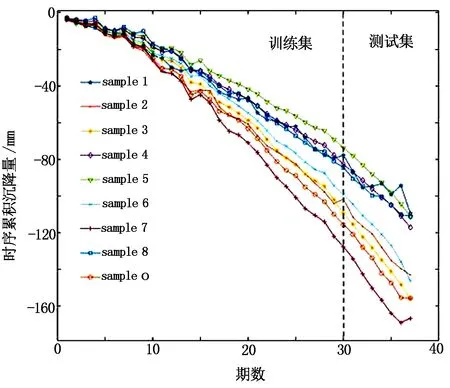
图4 各样本点沉降变化曲线

2.3 模型沉降预测及结果分析

本文将SBAS-InSAR的前30期监测数据作为训练集，对后7期(2020年3月28日-2020年6月8日)的数据进行预测，并将后7期SBAS实际监测值与预测值进行对比分析。表1为各个模型的前30期拟合度(以sample 1为例)，表中的R2为模型的判定系数，MAE为平均绝对误差，RMSE为均方根误差。表2为各个模型的预测值与相对误差(以sample 1为例)。

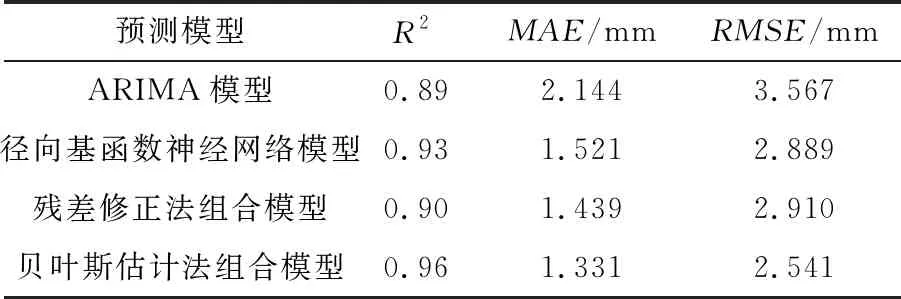
表1 各个模型的拟合度

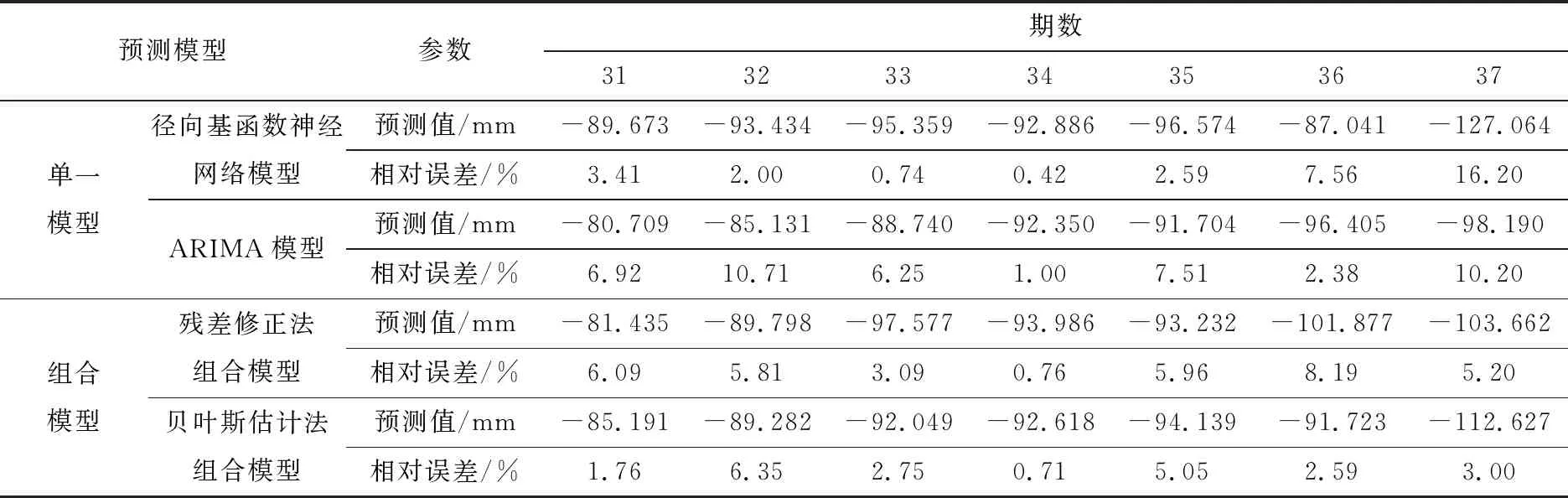
表2 各个模型预测值与相对误差

为验证上述4种预测模型的有效性，以9个样本点预测值的MAE、MAPE(平均相对误差)、RMSE为评价指标，计算公式分别见式(16)、式(17)、式(18)，计算结果见表3。

(16)

(17)

(18)

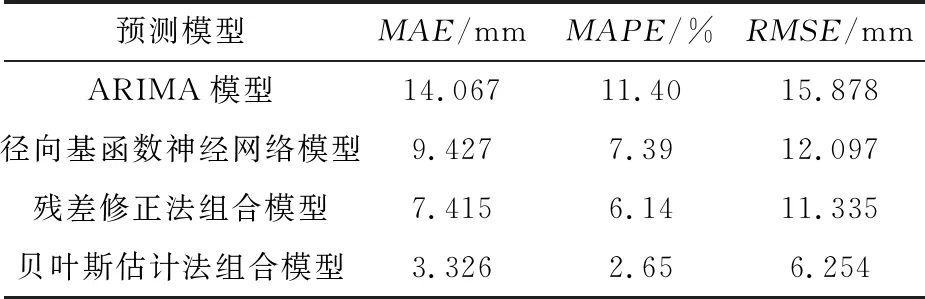
表3 不同模型预测精度比较

从表3可以看出：ARIMA模型的MAPE达到了11.40%(一般认为MAPE低于10%时，模型可以使用)，单一的ARIMA模型在中长期地表沉降预测中应用效果较差；而单一的径向基函数神经网络模型各项性能指标均优于单一的ARIMA模型，可以满足中长期地表沉降预测的基本需求；基于贝叶斯估计法和残差修正法的两种组合模型的MAE和MAPE以及RMSE指标均优于单一模型，但是残差修正法组合模型与径向基函数神经网络模型相比，各项性能指标的差距均不大；贝叶斯估计法组合模型相对其他3种模型的各项指标均有较大提升，为最佳预测模型。

3 结论

以金川硫化铜镍矿龙首矿西二采为研究对象，采用38景SAR影像进行SBAS-InSAR地表沉降监测，得到该地区37期累积沉降量，根据9个样本点的前30期累积沉降数据建立4种模型，分别计算得到后7期的预测值，并将其与实际值比较来测试4种模型的精度和适用性，得到以下主要结论：

a.基于残差修正法将ARIMA模型和径向基函数神经网络各自的优势进行组合，采用贝叶斯估计法根据两种单一模型当前时刻之前的预测表现对单一模型动态赋权，有效克服了单一模型的缺陷。预测实验结果表明：两种组合模型精度均优于单一模型，可以应用于矿山地表沉降预测。

b.基于贝叶斯估计法的ARIMA和径向基函数神经网络组合模型的性能不仅优于单一模型，而且与基于残差修正法的组合模型相比，其性能有大幅提升，得到的MAE为3.326 mm、MAPE为2.65%、RMSE为6.254 mm。

c.本文提出的基于贝叶斯估计法的组合预测模型有效提高了模型的预测精度，为矿山地下开采引起的地表沉降预测提供了另一种有效方法。