Ω涡识别方法在双进口两级中开泵中的应用

赵建涛，袁建平 *，裴吉，王文杰，张本营

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013; 2. 山东双轮股份有限公司，山东 威海 520000)

双进口两级中开泵因其流量大、扬程高等特点，被广泛应用于提水灌溉、远距离调水等工程领域.该类型泵具有比一般离心泵更复杂的结构，其内部流动复杂，极易诱发泵内不稳定流动.有研究表明，泵内部的不稳定流动与其涡旋的产生、发展及耗散密切相关[1].因此，利用涡识别技术研究泵内部流场涡的演变过程，对其稳定运行具有重要意义.

在流体机械领域应用较广的涡识别方法有涡量法、Q准则、λ2准则、λci准则等[2].敏政等[3]基于DDES湍流模型，通过涡动力学分析了多工况下离心泵内的涡旋分布情况，发现蜗壳内涡旋主要集中在隔舌区域及蜗壳进口区域，并随流体一起运动.曹璞钰等[4]通过对离心泵叶片吸力面的拓扑结构分析，利用Q准则捕捉到与压气机中的Spike式失速类似的双龙卷分离涡结构.这些传统的涡识别方法在实际应用中严重依赖于具体算例相关的阈值，并且受剪切流动影响.为了解决阈值问题，LIU等[5-6]提出了一种量纲一化的Ω方法识别涡结构，并成功应用于边界层转捩等多种经典流动问题中.与传统的Q准则和λ2准则相比较，Ω涡识别方法具有明确的物理意义，对阈值选择不敏感且可以同时捕捉强涡及弱涡[7].杨宝锋等[8]进一步确定了Ω涡识别法在高速离心泵流场涡结构捕捉方面的优势，并利用该方法对涡轮氧泵中离心轮与扩压器之间的动静干涉机理进行了阐释.

然而，目前对双进口两级中开泵的内流场分析多集中于压力脉动和常规性能的预测，对泵内部涡旋捕捉和相关判别准则的研究却较少涉及.文中以BB1T200-480型双进口两级中开泵为研究对象，利用Ω涡识别方法对泵内部涡旋结构进行捕捉，并与传统的涡识别方法Q准则、λ2准则进行对比分析，验证Ω方法在研究双进口两级中开泵内部涡识别的可行性，从而为双进口两级中开泵的优化设计提供一定的理论依据.

1 数值计算

1.1 计算模型

研究对象为某一台具有两端进口、中间出口且结构对称的两级中开泵，该泵设计性能参数分别为流量Qd=540 m3/h，扬程Hd=120 m，转速n=1 490 r/min.利用三维UG建模软件对水体域进行三维造型，将吸水室进口及压水室出口均延长5倍管径长度管路，以减少数值计算过程中进出口流动对泵内流场以及收敛性等的影响.计算模型如图1所示.

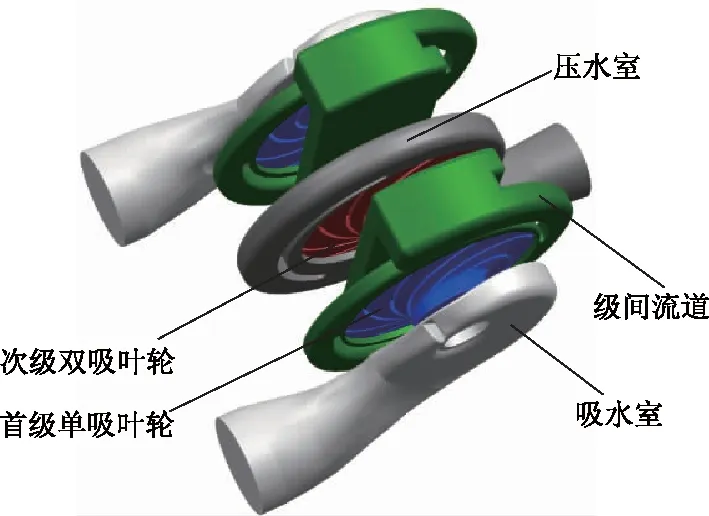
图1 双进口两级中开泵计算模型

1.2 网格划分及收敛性分析

为确保网格加密因子略大于1.3，文中设置3种类型网格，其中细密网格数为2 943万，中等网格数为1 285万，糙网格数为567万.各过流部件的网格数N如表1所示.

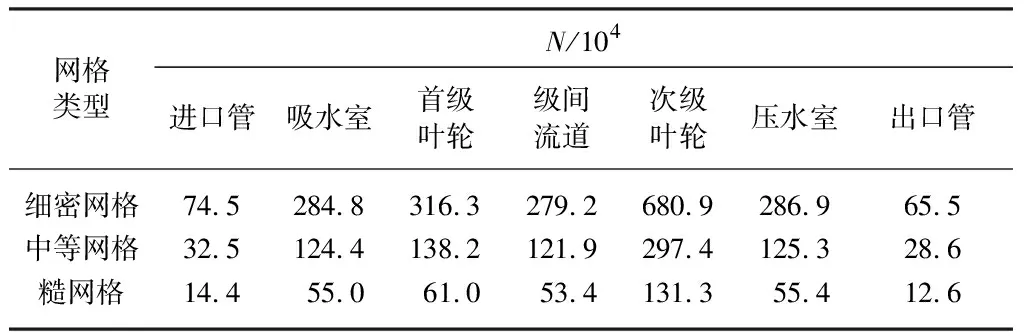
表1 各过流部件网格数

为了确保数值计算结果的准确性，采用基于理查德外推法的网格收敛指数(GCI)进行网格离散误差的估计[9].离散值越接近精确解，离散误差就越小，GCI值也越小.

在设计工况下进行网格收敛性分析，选取泵扬程H和首级叶轮叶片力矩T作为判断指标，计算结果如表2所示，表中下标1，2和3分别对应不同类型的网格，φ1，φ2和φ3分别表示3种网格下计算得到的关键变量值.

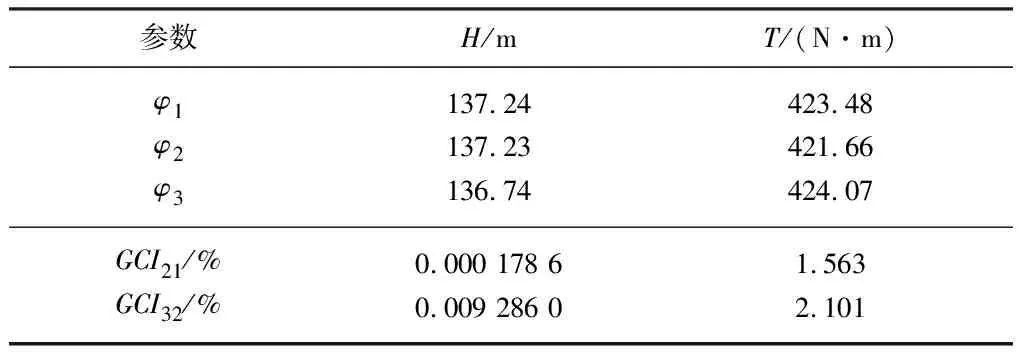
表2 数值计算离散误差统计表

由表2可知，对于不同的判断指标，网格收敛指数均小于3%，满足网格收敛指数准则[10].为了保证计算精度且能更好地捕捉小尺度涡，文中选择Fine网格进行计算.两级叶轮及吸水室等壁面平均y+<10,其余壁面平均y+<300，以满足SSTk-ω湍流模型对近壁面网格质量的要求，保证模拟的准确性.

1.3 边界条件设置

应用计算流体动力学商业软件CFX对计算模型进行非定常计算，选用SSTk-ω湍流模型[11]求解非定常雷诺平均动量方程.

在进口边界设置总压进口，出口边界设置质量流量出口，计算壁面采用无滑移边界条件，近壁面处采用自动壁面函数处理.之后，将定常计算结果作为此次非定常计算的初始流场，收敛精度设置为10-5，时间步长设置为0.335 6 ms，即叶轮每转动3°的时间为1个时间步长，总时间设置为0.322 1 s，即叶轮旋转8周.

1.4 试验验证

为保证数值计算结果的准确性，在开式试验台上对双进口两级中开泵进行外特性试验验证.图2为试验与数值计算的结果对比，其中各工况点的计算值是非定常计算下最后3个周期的时均扬程和时均效率.由图2可以看出，计算扬程与试验扬程基本一致，计算效率的趋势与试验效率的趋势也基本相同，这表明文中所采用的数值计算方法和计算模型有较高的可靠性.

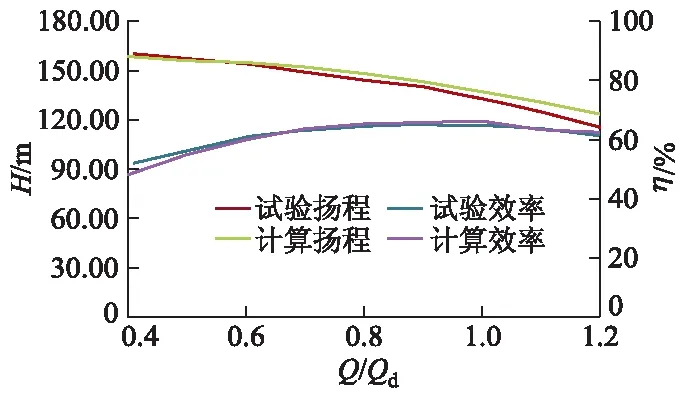
图2 泵数值计算与试验外特性曲线对比

2 涡识别准则简介

Q准则、λ2准则和Ω方法都是基于速度梯度张量▽V的分解.▽V可以被分解为两部分，即一个对称张量A和一个反对称张量B，分别代表流场中某一点的变形和旋转，即

(1)

(2)

2.1 Q准则

Q准则基于速度梯度张量的第二矩阵不变量[12]，其表达式为

(3)

其中‖‖F表示矩阵的Frobenius范数.Q>0表示在流动中旋转占主导地位，Q越大，则表明此处流体旋转率越大，存在涡旋的可能性也越大.

2.2 λ2准则

λ2准则是对搜索压力最小值区域方法的改进，当对称张量A2+B2存在2个负特征值时，压力在由这2个负特征值对应的特征向量张成的平面内为极小值.因此将特征值按λ1>λ2>λ3进行排序，当λ2<0时，压力存在极小值，即存在涡旋区域.

2.3 Ω方法

Ω方法的物理意义是旋转部分涡量大小占总涡量大小的比例，即

(4)

式中：ε为一个正数，其目的是为了避免分母为0.

由式(4)可知，Ω的取值范围为0≤Ω<1.当Ω>0.5时，表示反对称张量B相对于对称张量A占优，因此可以采用Ω略大于0.5来作为涡识别的判断依据.根据LIU等[6-7]的研究，在实际应用中，一般可以选取Ω=0.52作为固定阈值来识别涡结构.

3 结果与讨论

3.1 δ取值

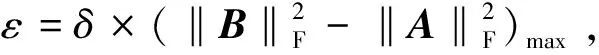
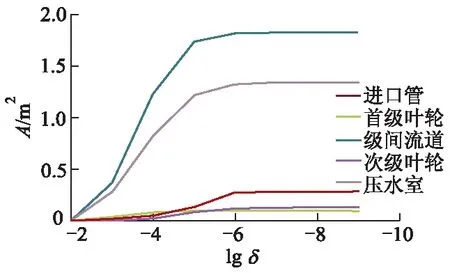
图3 不同δ值的涡旋表面积量化统计

3.2 不同涡识别方法对比

为了研究不同涡识别方法在双进口两级中开泵内流场中涡旋结构捕捉方面的适用性及准确性，将传统的涡识别方法Q准则、λ2准则及新的涡识别方法Ω方法应用于设计工况下双进口两级中开泵内流场的研究中，并对不同的涡识别方法进行对比分析.已有研究表明，Q准则、λ2准则对阈值的选取非常敏感，阈值大小对所识别出来的涡旋数量影响很大[2,8].这是因为Q值对应涡的强度，当Q值过大时，一些较弱的涡将无法被识别出来，λ2值的选取也与之相似.

因此，为了合理地选取Q值和λ2值，文中以识别出来的涡旋表面积为参考量，如图4统计直方图所示，当3种不同涡识别方法所识别出来的涡旋表面积近似相等时，认为选取的Q值和λ2值比较合理.由于在首级叶轮和次级叶轮处，Q准则和λ2准则这2种涡识别方法与Ω方法识别出的涡旋分布相差太大，所以上述方法对于这2处的阈值选择并不适用.

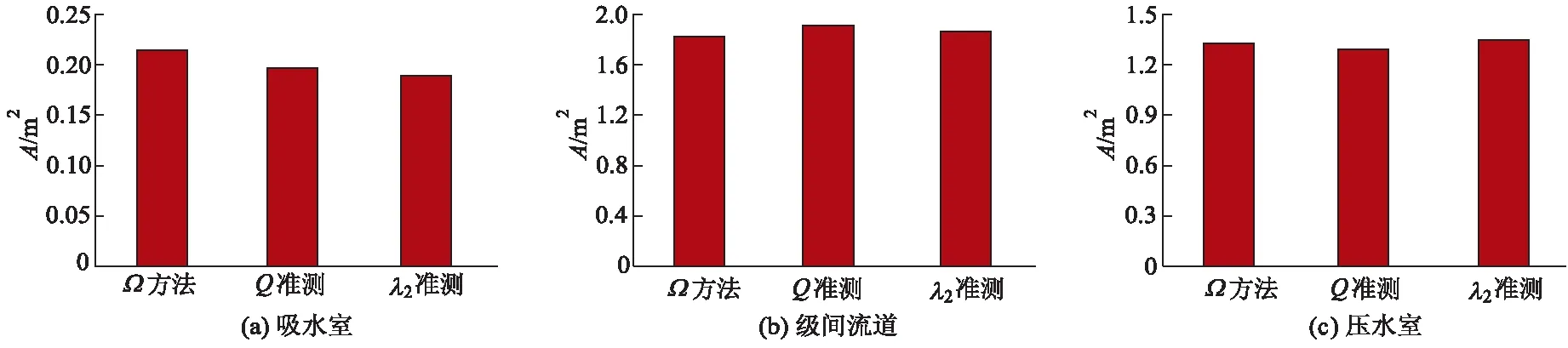
图4 不同涡识别方法涡旋表面积的量化统计

图5为吸水室、首级叶轮、级间流道、次级叶轮和压水室采用上述3种不同涡识别方法时内部涡旋结构分布，可以看出，在吸水室中，3种方法都能准确识别出口处的回流涡以及隔板处失速涡.但是相较于其他2种方法，Ω方法在隔板处能更多识别出一个长条状的涡带.同时，由于级间流道的正流道呈180°对称分布，所以3种涡识别方法所识别出来的涡旋分布也近似呈180°对称分布，Ω方法可以更加清晰地显示正流道的涡旋分布(见红色方框)，其他2种方法因为不能有效地消除壁面剪切层对涡识别的影响，因此不能清晰地显示出正流道内部的涡旋分布情况.

在反流道处，3种涡识别方法的识别效果几乎一致，都能显示出反流道中复杂的涡旋分布.在压水室中，与级间流道的涡识别效果相似，3种涡识别方法的识别效果也近乎一致，但是在压水室的扩散段，不同于其他2种方法识别的涡呈现不连续性和破碎性，Ω方法识别的涡更加连续且平滑.

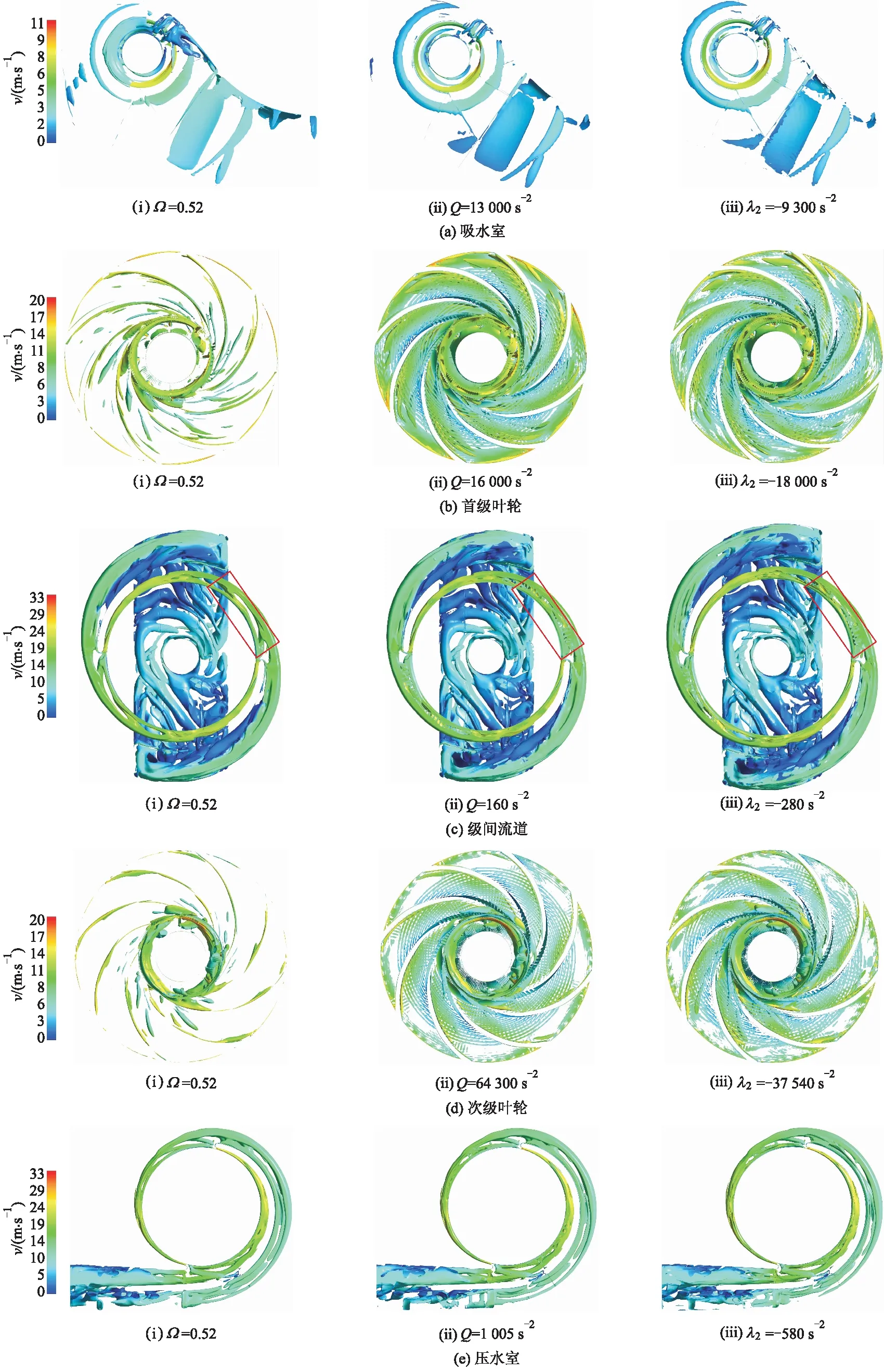
图5 基于不同涡识别方法的各过流部件涡旋分布

对比图5b和图5d可以发现，不同于静部件中的涡识别效果，Q准则、λ2准则和Ω方法在单级叶轮和次级叶轮这2个动部件中的识别效果相差很大.由于双进口两级中开泵中壁面的强剪切效应，Q准则及λ2准则的识别效果相似，都将叶片及叶轮前后盖板剪切层错误地识别为涡结构，这导致叶轮内部真实的涡结构被前后盖板的剪切层所覆盖，无法获得准确涡结构分布及演化过程.而Ω方法可以清晰地捕捉到叶轮进口的回流涡、叶片吸力面由于流动分离而产生的长条状涡团、叶轮流道里面的通道涡及次级叶轮尾缘处的尾迹涡.因此，Ω方法能将剪切和纯旋转运动区分开，获得较为清晰的泵内涡旋结构，有助于深入研究泵内涡旋产生、演化及脱落的过程及机理.

3.3 方法在反流道中的适用性分析及改进

由于级间效应等因素[15]，级间流道对双进口两级中开泵的扬程和效率具有很大影响.级间流道的反流道中涡旋数量众多且分布杂乱(见图5c)，因此，在确定Ω方法在反流道中的适用性后，可以为级间流道的结构优化提供有力的理论支撑.

图6为3种典型工况下反流道中截面的速度流线和涡旋分布，可以看出：3种工况下反流道都存在大量的涡旋，且大尺度涡旋集中在反流道的壁面附近，这可能是由于反流道与过桥段组成近似于直角流道，从而导致流体在由过桥段向反流道过渡的过程中，速度方向由周向向轴向突变产生了涡旋；随着流量的增大，在惯性的作用下，流体在反流道出口附近开始形成涡旋；在1.0Qd和1.2Qd工况下，Ω方法准确地捕捉到了特别小尺度的涡旋.

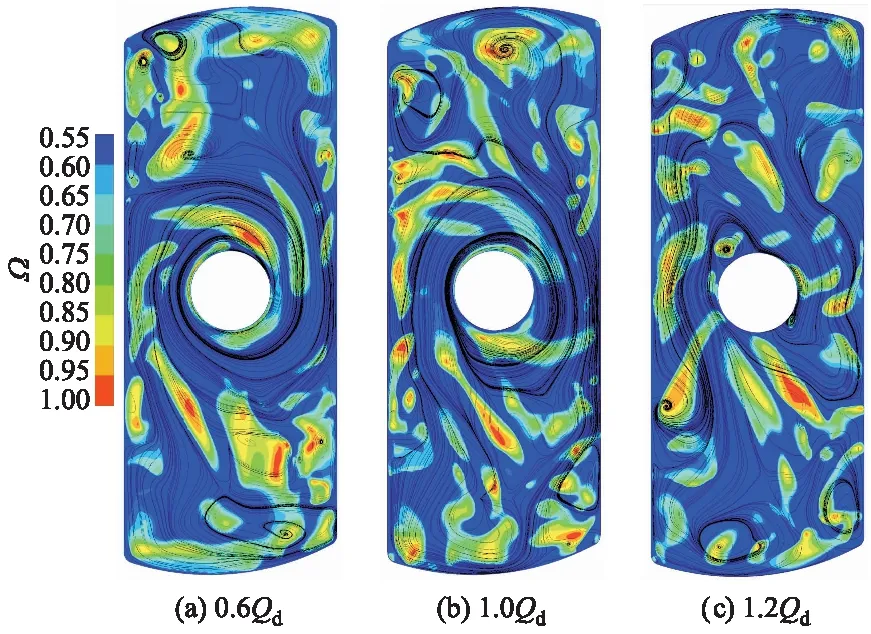
图6 反流道中截面流线和涡旋分布

由图6还可以看出，反流道中小部分区域Ω强度分布与速度流线并不有效对应，虽然这些区域的流线都呈现强扭曲的趋势，但是会对后续反流道中涡演化过程分析造成很大困扰.

ZHANG等[16]在研究普通单级离心泵射流尾迹结构时，只选取涡量在Z轴即旋转轴的分量来分析尾迹涡演化的过程.因此，文中基于同样的思路将Ω方法进行改变，将对称张量A和反对称张量B降维到XOY平面上，即

(5)

(6)

(7)

基于新的表达式得到的反流道中截面速度流线和涡旋的分布，如图7所示.可以看出，相较于之前未降维的Ω方法，新的方法得到的云图与速度流线图更加对应，同时规避了之前许多没有形成涡旋而流线呈现出强扭曲的区域.这说明在反流道中的涡旋以轴向涡旋为主，并且在研究涡演化的过程中，可以将Ω方法进行适当降维处理以得到更加清晰准确的涡分布情况.

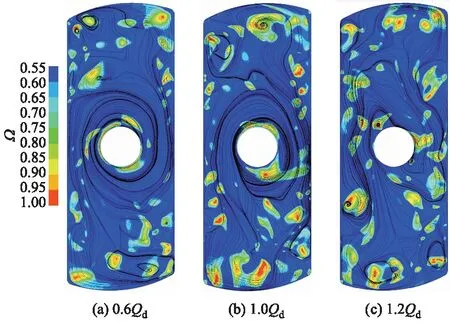
图7 降维后反流道中截面速度流线和涡旋分布

4 结 论

1)Ω涡识别方法具有对阈值选择不敏感和可以避免壁面强剪切层对泵内识别效果的影响等优势，因此，可作为双进口两级中开泵内涡识别的有效方法.

2) 将Ω方法简化到XOY平面后，其在反流道中的适用性更好，可以为后续的反流道结构优化提供一定的理论依据.