基于相关性分析的Bi-LSTM测井曲线预测方法
查文舒,乔 奇,刘子雄,李道伦
(1.合肥工业大学 数学学院,安徽 合肥 230601; 2.中海油田服务股份有限公司 油田生产研究院,天津 300450)
测井数据在研究地层结构和地下油气资源分布起到至关重要的作用,地质勘探工程师通过对测井数据的分析可以清晰地摸清地下油气储层集的状况,并以测井数据为基础建立更为准确的地质模型。然而在现实开采的过程中,由于地壳自然变动和一些人为干预,经常会出现测井数据与真实数据相差很大或者缺失的情况,重新测井会付出很多人力和物力。为了避免资源浪费,研究者根据已获得的数据生成目标测井曲线。在没有机器学习和深度学习的情况下,研究者提出根据地质信息建立一些模型预测油气田产量[1]和反演测井曲线[2]。然而有些物理模型是在研究者自己定义的很多假设情况下建立的,没有以真实的复杂地层情况为依据,在建立模型时也掺杂着研究者的主观考虑,可能导致生成的测井曲线与真实的测井曲线存在较大差异。此外,由于各种测井数据之间存在不同的内在联系,部分研究者应用一些传统的分析方法(如回归分析法、GIS组件技术等)完成对测井曲线的生成[3-4]。但是,由于地下情况和地质存在很强的不确定性,数据间的映射关系也表现得极其复杂,传统方法的预测效果不是很理想。
近年来,随着机器学习和神经网络的发展,人工神经网络方法逐渐在科学和工程领域得到广泛的应用,不少研究者使用人工神经网络预测测井曲线[5]、气井积液[6]、碳酸盐岩储层孔隙度[7]和水合物的生成[8]。人工神经网络是一种点对点的映射关系,与传统的预测方法相比,这种方法能够反映测井数据之间存在的非线性关系。但是这种方法忽略了测井曲线随深度变化的影响和数据的前后联系,尤其是无法有效处理序列数据问题[9],违背了地质学分析思想,因此生成的测井曲线的准确性需要进一步提高。
人工神经网络对先前的信息无法进行保存和利用,不能预测与序列有关的数据,有研究者通过结合小波变换[10]、奇异谱分析[11]等一系列方法,对人工神经网络进行改进,但是改进效果并不理想。随着智能时代的到来,循环神经网络(recurrent neural network,RNN)[12]逐渐被地质研究者所应用,RNN单元内存在一个自循环结构,可以使上一个序列特征输出与下一个序列特征输入一同作为模型的输入被传送到网络模型中,保留了之前状态的信息,解决了数据之间前后互相影响的问题。RNN在学习过程中可以使有效信息在网络中流动使用,基于RNN的方法不仅考虑了各条测井曲线之间的相互联系而且还展示出测井曲线随井深度变化的趋势,符合地质学分析思想。
长短期记忆(long short-term memory, LSTM)[13]神经网络是一种改进和完善的RNN模型;该网络架构通过对细胞单元精心设计,将“门”结构使用在每个自循环结构中,通过“门”结构模仿生物神经元信息的传导模式,对信息去除和保留做出选择,解决了普通RNN中梯度产生的问题。在机器翻译评测[14]、交通流预测[15]、故障时间序列预测[16]等领域都取得了较好的结果。部分学者运用LSTM网络方法进行了测井曲线的补全与人工合成[17]、储层物性参数预测[18]、钻前测井曲线预测[19]等,也取得了较好的效果。双向长短期记忆(bidirectional long short-term memory, Bi-LSTM)[20]神经网络增加了从后向前的计算过程,对全局的概念有更好的掌握。已有学者运用Bi-LSTM研究监控机器健康[21]、英语阅读理解[22]等,也都取得了较好的效果。
相关系数是衡量数据之间是否有联系的量,相关系数的大小可以反映数据之间相关程度的高低。在同一地层下,不同测井曲线之间也会存在不同的相关性,根据相关性的大小,选择合适的预测模型,在一定程度上能够减小样本数据,提高预测精度。本文利用测井曲线之间的相关性,使用Bi-LSTM,完成对测井曲线的预测。
1 神经网络原理
1.1 RNN
RNN的输入不同于一般的神经网络,它是基于时间特殊性考虑的,每个单元的输入不仅包含了当前需要输入的信息,而且还包括前面状态的信息。RNN的展开示例如图1所示。

图1 RNN的展开示例
从图1可以看出,RNN实质上是对序列中的每个单元作同样的计算,循环的过程就就是对h连续执行的过程。
1.2 LSTM神经网络
在实际操作的过程中,RNN仅对前面几步的信息有记忆,不能做到很长时间的记忆,因此一般结构的RNN逐渐淡出了大家的视野。文献[13]提出LSTM神经网络结构,大大延长了记忆周期,可以保留之前很长时间的信息。LSTM单元细胞结构如图2所示。
LSTM可以通过一个特殊的结构“门”精准地控制单元状态信息的增加和减少。“门”会控制信息传输的比例,下面对所谓的“门”结构进行解释。

图2 LSTM单元细胞结构
第1个“门”是遗忘门,它的作用是将一部分信息从单元状态中删除。起决策作用的是sigmoid层,遗忘门根据之前的状态向量值st-1和当前的输入向量值xt对所有的单元状态做出选择。遗忘门表达式为:
ft=σ(Wf[xt,st-1]+bf)
(1)
其中:σ为激活函数;Wf为权值矩阵;bf为偏置项。
第2个“门”是输入门。RNN不仅需要“忘记”之前的部分信息,重要的是补充最新的信息到记忆中,这就需要通过输入门来完成这一操作,它可决定单元状态中哪些新信息可以被保留下来,输入门表达式为:
it=σ(Wi[xt,st-1]+bi)
(2)
其中:Wi为权值矩阵;bi为偏置项。
(3)
其中:Wc为权值矩阵;bc为偏置项。
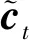
(4)
其中,*为哈达玛积。
第3个“门”是输出门,表达式为:
ot=σ(Wo[xt,st-1]+bo)
(5)
其中:Wo为权值矩阵;bo为偏置项。
当前时刻的单元状态值ct有多少信息可以作为LSTM的输出,st由输出门ot和tanh共同决定,表达式为:
st=ottanhct
(6)
1.3 Bi-LSTM神经网络
Bi-LSTM网络模型结合时间序列起始点和终点各自执行的LSTM,输出结果由向前和向后的LSTM状态同时决定。Bi-LSTM网络模型的示意图如图3所示。

图3 Bi-LSTM模型
2 基于测井曲线相关性的Bi-LSTM预测
2.1 测井曲线相关性分析
检验各变量之间是否存在相关性可以对其作相关性分析,可以了解变量之间的变化趋势,确定变量间是否存在关联,对变量数据有初步的了解。因此本文对一些已知的测井曲线进行相关性分析,通过曲线之间的相关性程度大小选择合适的测井曲线,再利用神经网络预测其他测井曲线,不仅大大节省了计算量,而且使预测精度大大提高。相关系数计算公式为:
(7)
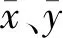
2.2 数据预处理
本文采用MinMaxScaler归一化方法对神经网络的输入数据进行处理,使得各种测井数据处于合理的分布范围,防止输入数据之间不同数量级影响预测结果。归一化的计算公式为:
(8)
其中:x为输入的测井数据样本;x′为归一化的测井数据;xmin为样本中的最小值;xmax为样本中的最大值。对测井数据进行归一化处理,不仅没有改变数据间存在的相关性,而且还解决了数据间不同数量级和取值范围的影响。
2.3 网络训练模型
Bi-LSTM网络模型的训练过程大体上可以分为如下5个步骤:① 从训练序列起始点向前执行,计算Bi-LSTM的输出值;② 从训练序列终点向后执行,计算Bi-LSTM的输出值;③ 将输出值与真实值进行比较,计算两者之间的误差,然后按照与步骤① 和步骤② 计算相反的方向计算隐藏层之间和各细胞单元之间的误差;④ 根据步骤③计算的误差,分别计算各自对应的权重和偏置梯度;⑤ 根据梯度,应用Adam优化算法[22]对相应的权重和偏置进行更新,输出预测的测井曲线序列。
Bi-LSTM网络训练预测框架流程图如图4所示。

图4 Bi-LSTM网络训练预测框架
2.4 评价方法
本文采用均方误差(mean square error)EMS、平均绝对误差(mean absolute error)EMA对预测效果进行评价,其计算公式分别为:
(9)
(10)
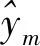
3 实 验
为了测试Bi-LSTM的预测效果,从以下2个实验进行验证:Bi-LSTM与LSTM预测对比实验、基于测井曲线相关性预测测井曲线实验。实验目的如下:
(1) 对比Bi-LSTM与LSTM的性能。
(2) 评价Bi-LSTM基于测井曲线相关性预测其他测井曲线的能力。
3.1 Bi-LSTM与LSTM预测对比实验
本实验采用的是某致密气井的真实测井数据,分别利用LSTM和Bi-LSTM基于同一口井中的测井曲线进行预测,并对比2种方法所预测生成的曲线的准确度。从井中获得测井曲线有井斜DEV、伽马GR、光电吸收截面指数PE、孔隙度POR、泥质含量VSH、垂直校正砂岩含量VSND、有机含碳量TOC和补偿中子CN 等8条测井曲线。测井段井深为2 700~4 500 m,总长为1 800 m,取样间隔为0.1 m。训练集由2 700~4 100 m测井段组成,测试集由4 100~4 500 m测井段组成。实验中训练数据有14 000组,测试数据有4 000组,利用DEV、GR、PE、POR、VSH、VSND、TOC的7条测井曲线作为模型的输入预测测井曲线CN。采用单向LSTM和Bi-LSTM 2个模型,模型中分别包含2个长短期记忆层,其中隐藏单元个数是50,模型最后再接一个全连接层,用来输出结果。为了防止出现过拟合,模型中加入丢弃率为20%的丢弃操作(dropout)。LSTM模型和Bi-LSTM模型对CN曲线的预测结果如图5、图6所示。
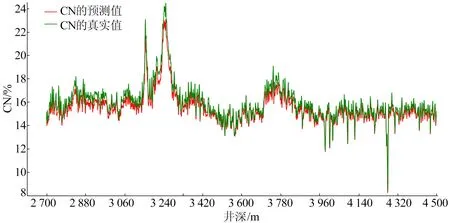
图5 单向LSTM模型对CN曲线的预测结果
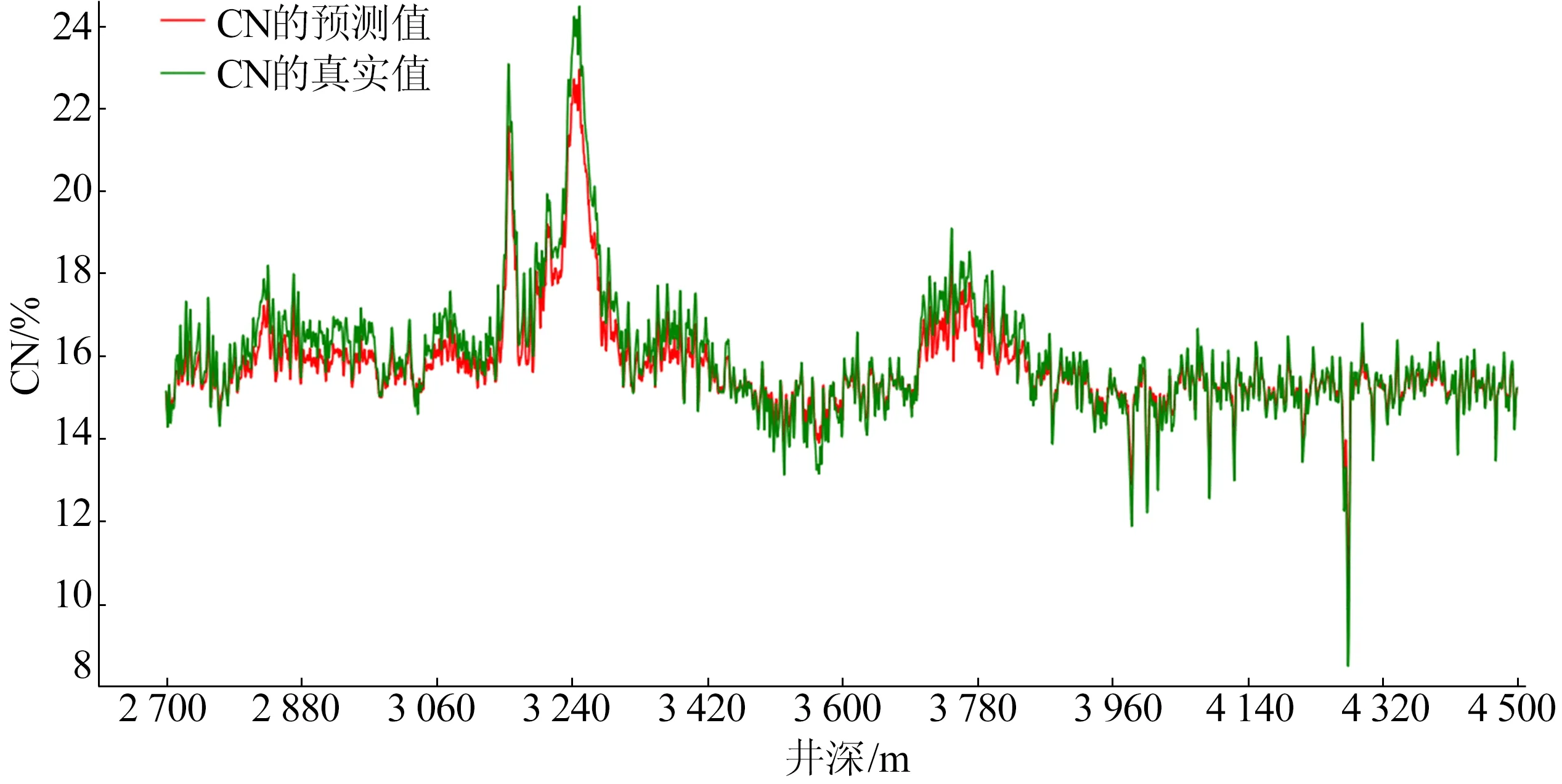
图6 Bi-LSTM模型对CN曲线的预测结果
从图5可以看出,LSTM模型的预测值与真实值存在较大的误差。从图6可以看出,Bi-LSTM的整体预测结果比LSTM模型更加接近真实值,能反映测井曲线的真实变化情况,预测精度比LSTM模型有显著的提高。LSTM和Bi-LSTM 2种模型预测误差值见表1所列,其中EMS减小58.6%、EMA减小38.2%。结果表明,Bi-LSTM模型比LSTM模型预测精度有很大提高,预测结果更加具有可信度,在测井曲线预测方面,Bi-LSTM模型更加实用和有效。

表1 LSTM与Bi-LSTM误差值表
3.2 基于测井曲线相关性的Bi-LSTM预测方法
本实验采用的是某地区致密气井的测井曲线,包含声波时差AC、井径CAL、补偿中子CN、井斜方位DAZ、密度DEN、井斜DEV、伽马GR、光电吸收截面指数PE、渗透率PERM、孔隙度POR、有机碳含量TOC、垂直校正白云岩含量VDOL、垂直校正白灰岩含量VLIM、垂直校正砂岩含量VSND和泥质含量VSH 15条测井曲线。测井段井深为2 700~4 500 m,总长为1 800 m,取样间隔为0.1 m。实验共有14 000组训练数据,4 000组测试数据,训练集由2 700~4 100 m测井段组成,测试集由4 100~4 500 m测井段组成。采用Bi-LSTM模型,由2个记忆层和1个全连接层构成,其中记忆层中隐藏元个数为70。为了避免出现过拟合的情况,模型中加入了丢弃率为30%的丢弃操作(dropout)。
在对测井曲线VSH做预测之前,计算VSH与其他测井曲线之间的相关系数,计算结果见表2所列。

表2 VSH与其他测井曲线之间的相关系数
为了检验基于相关性分析的Bi-LSTM测井曲线预测方法的性能,分别做了3次测井曲线VSH的预测实验,并对比预测结果。实验一,使用除VSH以外的全部测井曲线(AC、CAL、CN、DAZ、DEN、DEV、GR、PE、PERM、POR、TOC、VDOL、VLIM、VSND)作为Bi-LSTM模型输入预测测井曲线VSH;实验二,使用相关系数绝对值在0.5以上的测井曲线(AC、CN、DEN、DEV、PERM、POR、TOC、VLIM、VSND)作为Bi-LSTM模型输入预测测井曲线VSH;实验三,使用相关系数绝对值在0.8以上的测井曲线(CN、DEN、DEV、PERM、TOC)作为Bi-LSTM模型输入预测测井曲线VSH。实验结果如图7~图9所示。
从图7可以看出,以未考虑相关性的测井数据作为模型的输入时,预测结果能描述曲线的大概走向,但是测试值与真实值存在一定的差距。
从图8中的预测结果,特别是2 700~2 800 m、3 420~3700 m和3 870~4 500 m深度段(见图8蓝色虚线框)的预测结果可以看出,预测值基本与真实值相重合,整体的预测误差也有明显减小,其误差值见表3所列;其中输入相关性在0.5以上的曲线与输入未考虑相关性的测井曲线相比,EMS减小19.5%、EMA减小29.6%。
从图9可以看出,输入相关系数在0.8以上的测井曲线预测目标曲线时,整体预测效果比输入相关系数在0.5以上的测井曲线的预测效果有进一步的提升,其中3 420~3 690 m和3 900~4 500 m(见图9中蓝色虚线框)井段处的预测值更加接近真实值。

图7 未考虑相关性的预测结果

图8 输入相关系数在0.5以上测井曲线的预测结果

图9 输入相关系数在0.8以上测井曲线的预测结果
从表3可以看出,输入相关性在0.8以上的曲线与输入未考虑相关性的测井曲线相比,EMS减小32.5%、EMA减小35.2%;与相关性在0.5以上的测井曲线相比,EMS减小16.1%、EMA减小7.9%。这说明,Bi-LSTM结合曲线之间的相关性对测井曲线做预测,预测精度会随着相关性的增大而提高。

表3 Bi-LSTM模型预测误差值对比
4 结 论
LSTM模型和Bi-LSTM模型预测对比试验表明,考虑前后关联性,即基于Bi-LSTM的预测结果,EMS减小58.6%、EMA减小38.2%。这表明,考虑测井曲线前后关联性可以有效提高预测精度。
相对于不考虑相关性的结果,用相关系数在0.5以上的预测结果,EMS减小19%以上;使用相关系数在0.8以上的测井曲线进行预测,EMS比使用相关系数在0.5以上的结果减小16%。因此,预测精度会随着相关系数的提高而提高。
本文研究表明,若简单使用所有已知曲线,测井曲线预测精度可能会降低。考虑相关性后,使用更少的测井曲线且能得到更高的精度。因此,本文方法在测井曲线预测等方面有很好的应用前景。

