二维粒子运动模型的模拟和解析研究

2022-05-25 02:23楼鑫鑫丁中俊

合肥工业大学学报（自然科学版） 2022年5期

楼鑫鑫,丁中俊,田波

(1.合肥工业大学汽车与交通工程学院,安徽合肥 230009; 2.安徽农业大学工学院,安徽合肥 230036)

驱动扩散系统因其丰富而复杂的现象而备受关注[1]。相分离是在驱动扩散系统[2]中观察到的一种重要现象,在许多一维或准一维模型中都有提及,如ABC模型[3]、具有慢启动规则的交通流模型[4]、双车道模型[5]、一维硬粒子系统[6]等。

许多研究集中在二维驱动的扩散系统,文献[7]在二维周期网络上研究了丰富的相图,其中2种粒子以相反的方向运动;文献[8]在二维非对称简单排它过程中观察到2种干扰相;文献[9]在二维系统中研究了流体力学对液体混合物相分离后期动力学的影响;文献[10]在二维Lennard-Jones流体中分析了非平衡通道的形成,该流体由2个相反方向运动的颗粒组成;文献[11]提出2种胶体颗粒的二维模型,表明在驱动胶体系统中的通道形成,是宏观范围内的相变,但从无序的初始条件开始,在有限时间内不会发生宏观相分离;文献[12]的二维格子气模型中存在2种粒子,在外力的反向驱动下研究了“云”的粗化和动态标度;二维模型大多采用随机更新规则,考虑到一些应用背景(如行人对向流),文献[13]建立了一个具有并行更新规则与存在位置交换的二维驱动扩散系统,在该模型中,2种类型的粒子在二维网络上以相反的方向运动,当粒子发生冲突时根据周围环境判断是否发生位置交换,然后采用简单平均场方法对存在位置交换的二维驱动扩散系统进行了解析,但该方法并没有考虑粒子之间的相关性而使得误差较大。

本文以文献[13]为基础,建立存在位置交换的对向粒子流模型。然而粒子在实际的运动过程中存在相互作用,学者们将相关性[14]引入到简单平均场理论,得到簇平均场理论[15],也称作cluster平均场方法。本文采用簇平均场方法对模型进行解析,在解析中考虑粒子间的相关性,解析结果与仿真结果在均匀态下较为吻合,当出现堵塞带时误差仍然较大。

1 对向粒子流模型

本文基于元胞自动机建立对向粒子流模型,如图1所示。在一个网络中有N×N个格点,每个格点被一个粒子占据或者为空。系统中存在2类粒子,每个粒子可以向3个方向运动(图1a)。图1a中:PE(实心圆)为第1类粒子,向东、向北、向南跳跃的概率分别为q、(1-q)/2、(1-q)/2;PW(空心圆)为第2类粒子,向西、向北、向南跳跃的概率分别为q、(1-q)/2、(1-q)/2。

系统中有数量相等的2类粒子,粒子总密度为ρ,粒子的更新规则为并行更新,即每一个时间步,所有粒子同时进行更新;系统的边界为周期性边界,即系统中粒子数目保持不变。每个粒子先由其运动概率的大小来确定运动方向,再判断粒子运动的目标格点是否为空,若格点为空且同时没有其他粒子试图进入该格点,则该粒子在下一个时间步进入该格点;在同一时间步中,若有n个粒子可以进入同一个空格点,则以1/n的概率随机选择一个粒子进入该格点。此外,模型中还存在位置交换的规则,图1b中:在t时刻,若格点3的粒子PE试图向东运动,格点4的粒子PW试图向西运动,且1、2、5、6都被占据(含对角线的圆表示该格点可能被PE也可能被PW占据),则在t+1时间步这2个粒子以pe概率发生位置的交换;若1、2、5、6中有格点为空,则格点3、4的粒子不会发生位置交换。图1b的右图表示t+1时刻3、4格点的2个粒子成功发生交换,?表示1、2、5、6的状态不确定。

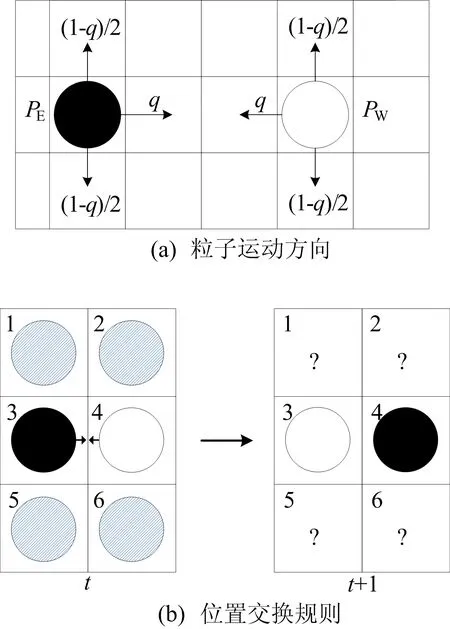
图1 对向粒子流模型

2 结果和讨论

2.1 模拟仿真

本文在一个尺寸为100×100的周期边界网格上进行仿真,即系统中存在100×100个格子。首先舍去前107个时间步使系统达到稳定,然后对后面的106个时间步进行统计,对每一种情况进行20 次仿真并计算平均值,得到考虑位置交换下粒子平均速度与密度的关系,如图2所示。

图2中:平均速度为粒子在每个时间步往目标方向运动的格点数;密度为系统中粒子数量占比。从图2可以看出,系统在任何密度下未出现完全堵塞,这是由于平均速度没有降至0。图2a中,粒子平均速度随着密度增加而一直下降,且系统中存在一个临界密度,当粒子密度超过这个值时,粒子的平均运动速度下降得更快。图2b～图2d中,平均速度随密度增加而下降,达到临界密度之后,平均速度增加,这是由于q值与pe值较大,当粒子数目较多时,相遇粒子之间的互换愈发频繁,使粒子可以运动。相比于图2b～图2d,图2a中粒子平均速度随着密度增加持续下降，这是由于此时q值与pe值较小,相遇的粒子之间发生位置互换的概率较小,从而相遇的粒子可以运动的概率也较小;当密度小于临界密度时,粒子处于均匀的状态,当系统中粒子较多时,系统中产生了一个堵塞带,阻止了系统运动,如图3所示。

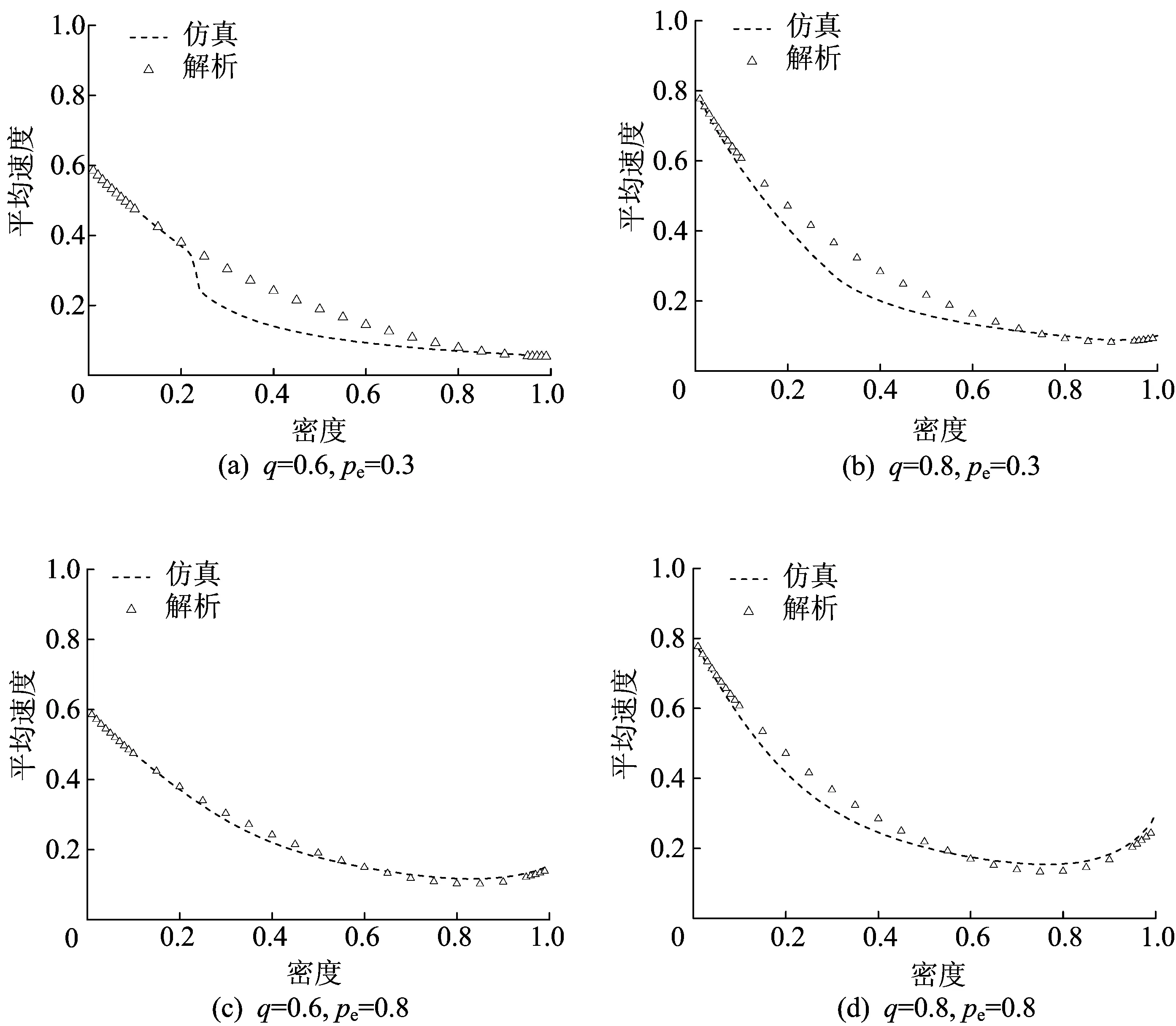
图2 在考虑位置交换的情况下粒子运动平均速度与密度关系

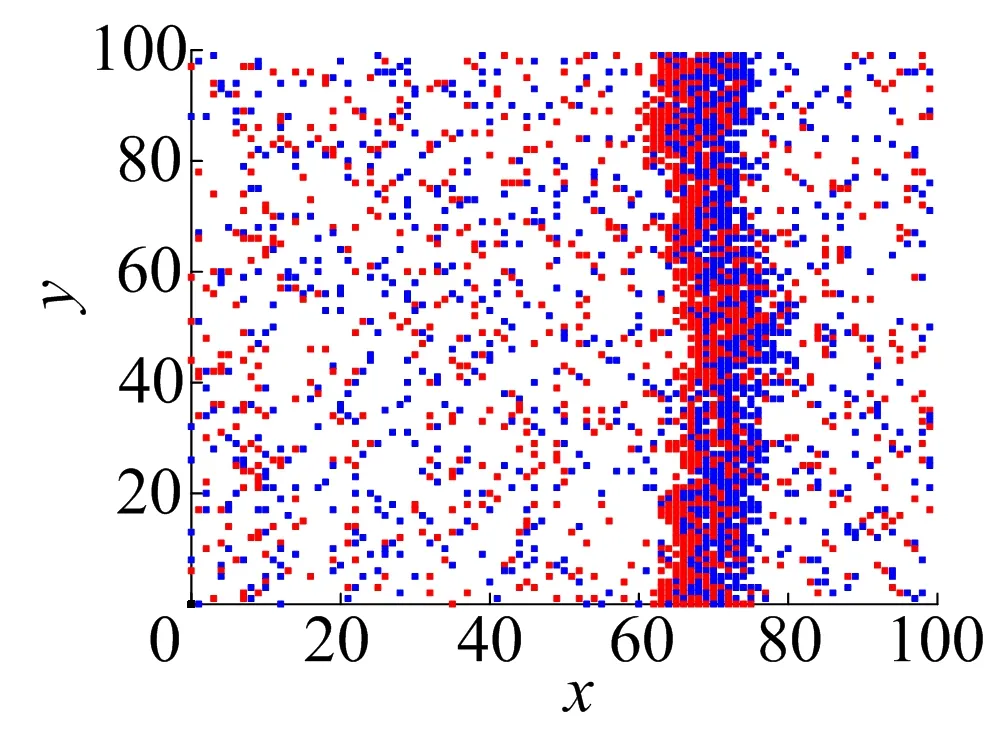
图3 q=0.6、pe=0.3的位形

2.2 2-cluster平均场解析法

本文使用2-cluster平均场理论方法解析对向粒子流模型,并分析粒子流的特性。在cluster平均场理论中,连续的n个格点即为n-cluster,相邻的2个格点即为1个2-cluster,记做(σi,σi+1)。σi=0,1,2(i=1,2),σi=0表示该格点为空;σi=1表示该格点被目标方向为东向的粒子占据;σi=2表示该格点被目标方向为西向的粒子占据。当vmax=1时,t+1时刻2-cluster(σi,σi+1)状态取决于t时刻4-cluster(σi-1,σi,σi+1,σi+2)的状态。当系统达到稳态后,出现2-cluster的概率为p(σ1,σ2)。

vmax=1时,2-cluster方程近似表达为:

p(σi,σi+1;t+1)=

p(τi-1,τi,τi+1,τi+2;t)

(1)

其中:p(τi-1,τi,τi+1,τi+2;t)为t时刻4-cluster(τi-1,τi,τi+1,τi+2)存在的概率;∑(σi,σi+1|τi-1,τi,τi+1,τi+2)为所有的4-cluster(τi-1,τi,τi+1,τi+2)更新成为2-cluster(σi,σi+1)的转化概率。

4-cluster(σi-1,σi,σi+1,σi+2)一共有81种位形可更新得到2-cluster(σi,σi+1),在不考虑位置交换的情况下,只有54种情况满足2-cluster平均场理论方程,如图4所示。图4中:第1列为粒子在t时刻的位形;第2列为粒子在t+1时刻的位形;第3列与第4列的乘积表示相应的转化概率。在系统中随机选择1个格点,格点为空的概率为1-ρ,被占据的概率为ρ。三角形和圆圈分别对应(σi,σi+1)中的σi与σi+1格点,且状态为空。箭头表示粒子运动的目标方向,→表示粒子目标方向为东向,←表示粒子目标方向为西向;?表示格点可能为空也可能被占据;ρ1表示东向粒子的密度,ρ2表示西向粒子的密度,2类粒子数相同时ρ1=ρ2;qs为粒子向其他方向运动的概率。

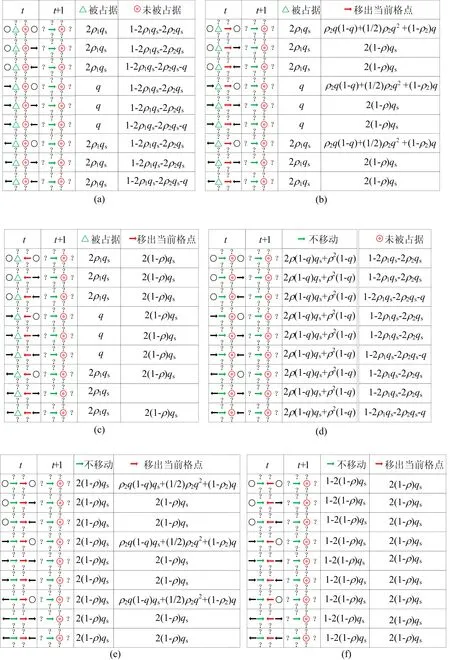
图4 能转化为p(1,0)的 4-cluster 的示意图及对应的转化概率

将格点进行1—12的编号,然后通过p(0,0,0,0)的例子介绍转化概率,如图5所示,其他概率以此类推。

图5中:t时刻1—4格点为空,5—12格点情况未知,可能被占据也可能为空;在t+1时刻有1个东向的粒子进入格点2,格点3依旧为空,即本文所求的p(1,0)。在模型中偏移概率的影响较小,为了解析的方便与清晰,忽略部分转移概率中偏移方向粒子的影响。

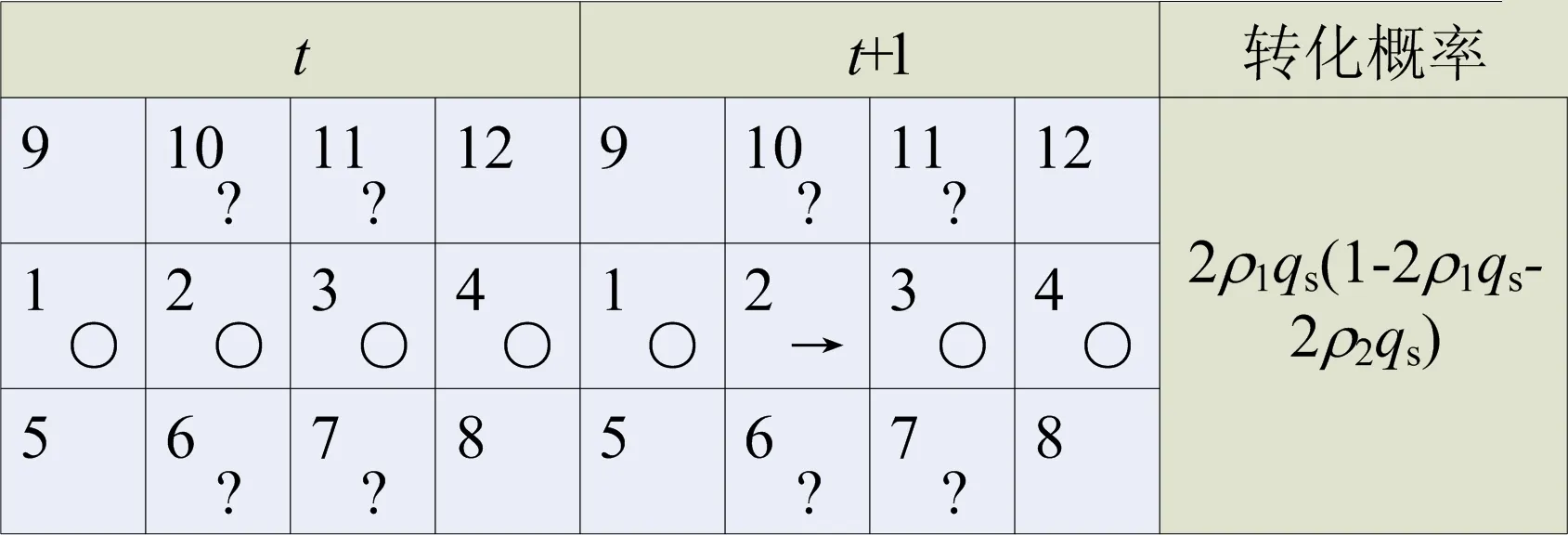
图5 图4中子图位形演化过程示意图

2ρ1qs表示格点2在t时刻为空,在t+1时刻被东向粒子占据的概率。在t时刻只有格点6或者格点10的东向粒子能在t+1时刻进入格点2号。格点6或者格点10被东向粒子占据的概率为ρ1,该粒子在t+1时刻进入格点2的概率为qs。因此格点2在t+1时刻被东向粒子占据概率为2ρ1qs。

1-2ρ1qs-2ρ2qs表示格点3在t时刻与t+1时刻都为空的概率。因为在t时刻只有格点7或者格点11的粒子能在t+1时刻进入格点3，所以存在2种情况:在t时刻格点7或者格点11被东向的粒子占据,该粒子在t+1时刻进入格点3,概率为2ρ1qs;在t时刻格点7或者格点11被西向粒子占据,该粒子在t+1时刻进入格点3,概率为2ρ2qs。因此格点3在t和t+1时刻都为空的概率为1-2ρ1qs-2ρ2qs。

其他情况以此类推。在2-cluster方法中,一共需要求解9个未知数,这9个未知数分别为p(0,0)、p(0,1)、p(0,2)、p(1,0)、p(1,1)、p(1,2)、p(2,0)、p(2,1)、p(2,2)。

通过系统中粒子的密度关系可得:

p(1,0)+p(1,1)+p(1,2)+p(2,0)+

p(2,1)+p(2,2)=ρ

(2)

p(0,0)+p(0,1)+p(0,2)=1-ρ

(3)

p(1,0)+p(1,1)+p(1,2)=

p(2,0)+p(2,1)+p(2,2)

(4)

模型中东向和西向粒子数量相等,根据对称性可得:

p(1,1)=p(2,2)

(5)

p(1,0)=p(0,2)

(6)

p(2,0)=p(0,1)

(7)

根据p(2,1)、p(2,0)粒子之间较弱的相关性假设,忽略相关性,即

p(2,1)=ρ2/4

(8)

p(2,0)=ρ(1-ρ)/2

(9)

将图4中所有子图的54种情况整合即可得到求解p(1,0)的总方程,即

p(1,0)=[p(0,0,0,0)+p(0,0,0,1)+p(2,0,0,0)+p(2,0,0,1)]2ρ1qs(1-2ρ1qs-2ρ2qs)+

[p(0,0,0,2)+p(2,0,0,2)]2ρ1qs(1-2ρ1qs-2ρ2qs-q)+

[p(1,0,0,0)+p(1,0,0,1)]q(1-2ρ1qs-2ρ2qs)+p(1,0,0,2)q(1-2ρ1qs-2ρ2qs-q)+

[p(0,1,0,0)+p(0,1,0,1)+p(1,1,0,0)+p(1,1,0,1)+p(2,1,0,0)+

p(2,1,0,1)][2ρ(1-ρ)qs+ρ2(1-q)](1-2ρ1qs-2ρ2qs)+

[p(0,1,0,2)+p(1,1,0,2)+p(2,1,0,2][2ρ(1-ρ)qs+

ρ2(1-q)](1-2ρ1qs-2ρ2qs-q)+

[p(0,0,2,0)+p(0,0,2,1)+p(0,0,2,2)+p(2,0,2,0)+p(2,0,2,1)+

p(2,0,2,2)](2ρ1qs)[2(1-ρ)qs]+

[p(1,0,2,0)+p(1,0,2,1)+p(1,0,2,2)]q[2(1-ρ)qs]+

[p(0,0,1,0)+p(2,0,1,0)](2ρ1qs)[ρ2q(1-q)+(1/2)ρ2q2+(1-ρ2)q]+

[p(0,0,1,1)+p(0,0,1,2)+p(2,0,1,1)+p(2,0,1,2)](2ρ1qs)[2(1-ρ)qs]+

p(1,0,1,0)q[ρ2q(1-q)+(1/2)ρ2q2+(1-ρ2)q]+

[p(1,0,1,1)+p(1,0,1,2)]q[2(1-ρ)qs]+

[p(0,1,1,0)+p(1,1,1,0)+p(2,1,1,0)][1-2(1-ρ)qs][ρ2q(1-q)+(1/2)ρ2q2+(1-ρ2)q]+

[p(0,1,1,1)+p(0,1,1,2)+p(1,1,1,1)+p(1,1,1,2)+p(2,1,1,1)+

p(2,1,1,2)][1-2(1-ρ)qs][2(1-ρ)qs]+

[p(0,1,2,0)+p(1,1,2,0)+p(2,1,2,0)+p(0,1,2,1)+p(1,1,2,1)+p(2,1,2,1)+

p(0,1,2,2)+p(1,1,2,2)+p(2,1,2,2)][1-2(1-ρ)qs][2(1-ρ)qs]

(10)

联立方程(2)～方程(10)可以解得9个未知数,得到p(1,0)计算模型中东向粒子的流率为:

J(ρ)=p(1,0)q1

(11)

其中,q1为p(1,0)中的东向粒子(1)在下一个时间步往目标方向东侧空格(0)运动的概率。q1的表达式为:

q1=[ρ23+2ρ1ρ22+ρ12ρ2][q(1-q)(1-qs)2+2(1/2)qqs(1-q)(1-qs)+

q(1-q)(1-qs)][(1/3)q2qs+(1/2)q2(1-qs)+(1/2)qqs(1-q)+q(1-q)(1-qs)]+

[2(1-ρ)ρ1(1-ρ2)+2(1-ρ)ρ2(1-ρ2)][q(1-qs)+(1/2)qqs]+

(1-ρ)2ρ2[q(1-q)+(1/2)q2]+(1-ρ)(1-ρ2)2q

(12)

为得到较为准确的速度,q1的计算要考虑p(1,0)中东向粒子(1)往目标格点(0)运动可能发生的竞争情况。当目标格点(0)南侧、北侧格点被任一种粒子占据,或目标格点(0)东侧格点被目标方向为西向的粒子占据时,就可能与目标粒子(1)发生竞争,因此方程(12)考虑了所有竞争的情况。

通过东向、西向粒子的对称性,解得系统中无位置交换部分的粒子平均运动速度为:

v(ρ)=2J/ρ

(13)

因为发生位置交换是2个粒子在目标方向上的运动,所以通过p(1,2)的位形可以计算位置交换的粒子流率,之前2-cluster方法已经得到p(1,2)的值,此时系统中所有粒子的流率计算方程为:

J1(ρ)=2J(ρ)+2p(1,2)ρ4q2pe

(14)

其中:ρ4为2个对向粒子的南北两侧相邻格点都被其他粒子占据的概率;q2为2个对向的粒子朝着目标方向运动;pe为位置成功交换的概率。通过对称性,得到粒子在位置交换时的流率。

系统中所有粒子的平均速度为:

v1(ρ)=J1/ρ

(15)

联立方程(2)～方程(15)得到存在位置交换规则下的解析结果(图2)。

从图2可以看出,解析结果与模拟结果较为吻合，随着密度的增加,解析与仿真之间的误差先增加再减小。这是由于当密度较小时,系统中实际发生位置交换的粒子较少,对粒子平均速度的影响小;随着密度的继续增加,粒子之间的相关性越来越强,而位置交换是影响速度大小的主要因素,2-cluster方法恰好考虑了该相关性,使求得的p(1,2)与实际值较为接近,从而使得解析与仿真结果较为吻合。

3 结论

本文以元胞自动机为基础建立周期边界的对向粒子流模型,在模型中存在2种目标方向不同的粒子,每个粒子有3个运动方向、1个目标方向与2个偏移方向,采用并行更新的规则。为了反映生活中粒子运动发生冲突的现象,在该模型中加入了一个位置交换规则。首先本文进行计算机模拟,然后通过2-cluster的平均场方法将二维问题划分成为2个一维问题,对是否存在位置交换的对向粒子流模型进行解析,并在该方法中考虑粒子之间的相关性。

在该模型中,模拟和解析均发现粒子的平均速度随着密度增加不会下降至0而发生完全堵塞;随着q或者pe的增大,则出现了平均速度随着密度增加先下降后上升的现象,因为在低密度时,系统中粒子数对平均速度产生较大的影响,而发生位置交换的粒子较少,所以位置交换对粒子的平均速度影响较小;而高密度下发生位置交换的粒子增多,成为影响速度的主要因素,从而使得粒子的平均速度增加。