基于改进A*算法的消防机器人路径规划算法研究

王 迪，黎 冠，李志伟，李明宇，谢家顺

(1.华北科技学院 安全工程学院，北京 东燕郊 065201;2.华北科技学院 电子信息工程学院，北京 东燕郊 065201)

0 引言

森林、高层建筑及危化品等火灾事故的发生，往往具有较大的破坏性，其造成的后果也普遍较为严重，近年来，天津港爆炸事故、四川凉山深林火灾等事故的发生，均造成了消防救援人员的巨大伤亡和不同程度的经济损失，给消防救援工作带来了巨大高效地开展何进一步快速、高效的开展消防救援工作，也成为了消防救援工作面临的主要问题。随着智能机器人技术的发展，一些具备自主移动、自主探测能力的消防机器人逐渐应用到消防领域当中[1]，并逐渐在消防救援中承担重要的角色。当出现火情时，消防机器人可快速深入到火源位置，及时扑灭火源，并配合消防救援人员开展现场火情勘察和人员搜救等工作，可进一步提高消防救援效率和保障消防救援人员的人身安全。

在消防机器人领域，路径规划算法作为消防机器人研究的重要方面，合理的路径规划策略可确保消防机器人安全、快速地进行救援和灭火工作，最大限度地减少人员伤亡和财产损失[2]。目前，常用的全局路径规划算法主要包括随机采样算法[3-4]、图搜索算法[5-6]和一些智能算法[7-9]等。本文将传统A*算法应用于消防机器人的路径规划中，但随着环境复杂度的增高，传统A*算法规划的路径结果中转折点较多，搜索效率明显下降。并且传统A*算法未能结合机器人本身的体积、物理学状态等因素，在实际使用过程中，需对其路径做进一步改进，以避免机器人与障碍物发生碰撞。在消防机器人路径规划算法的研究中，何光层[10]等利用改进A*算法解决室内智能消防机器人的全局路径规划问题。王宏北[11]等针对地形复杂，地貌特征易变的火场中消防机器人的路径规划问题，利用自适应改进蚁群算法来获取火场中的最优路径。

综上，本文针对消防机器人领域，利用传统A*算法导致的路径规划结果中存在过多转折点、搜索效率较低等问题，对传统A*算法的搜索邻域和轨迹方面进行改进，在邻域搜索阶段，将邻域子节点进行分级，依据优先级进行搜索，从而避免斜穿顶点问题的发生，使结果更符合实际环境要求。并利用改进Floyd算法去除冗余的转折点，增强路径的平滑性，进一步确保消防机器人路径规划结果的可行性。

1 传统A*算法

传统A*路径规划算法作为一种启发式搜索算法，常用在全局地图中搜索两点之间的最短路径。在A*算法的实现原理中，搜索区域被简化成一个二维数组，路径被描述为从起始栅格至终点栅格经过的所有栅格的集合，栅格的中心点则为节点n。A*算法的搜索方向是根据代价估算函数F(n)来确定的，如公式(1)所示，搜索过程中通过代价估算函数F(n) 来判断区域内当前点至目标点的距离，进而决定搜索方向。具体实现过程中，需要建立开启列表和关闭列表，开启列表中存储着所有可能出现在最终路径中的节点，关闭列表中存储着已检测并且不需要再次检测的节点。路径搜索过程中，首先需选取当前开启列表中F(n)值最小的节点，然后将其从开启列表中删除，再添加到关闭列表中，最终路径也将在关闭列表中产生。

F(n)=g(n)+h(n)

(1)

式中，F(n)为节点n的代价估算函数；g(n)为机器人从起始节点至当前节点n所花费的实际代价，一般情况下由当前节点的父节点的实际代价值得到；h(n)为启发函数，表示机器人从当前节点n至目标节点将要花费的预估代价。在传统A*算法中，分别采用曼哈顿距离与欧氏距离表示h(n)大小，两种表示方式如式2、3所示。

(2)

h(n)Manhattan=|xn-xt|+|xn-xt|

(3)

式中，xn，yn分别为当前节点n所处栅格的横坐标、纵坐标；xt，yt分别为目标节点所处栅格的横坐标、纵坐标。

2 改进A*算法

2.1 基于优先级的邻域搜索方法

在路径搜索的过程中，传统A*算法将机器人视为一个质点，未考虑机器人的体积等因素，其中，图1所示为一组传统A*算法规划的路径结果，该路径结果中，红色圆点位置出现路径斜穿障碍物顶点的问题，在实际使用A*算法的过程中，出现该问题时，机器人存在一定的安全风险。因此，为避免该问题的发生，本文对传统A*算法的搜索方向进行调整，将邻域中的节点划分优先级，分为优先组与普通组，如图2所示，N、E、S、W四个方向为优先组，其余NE、NW、SE、SW四个方向为普通组，在子节点的搜索过程中，首先对优先组中的子节点进行搜索，然后按照表1中的规则对普通组的子节点进行搜索。

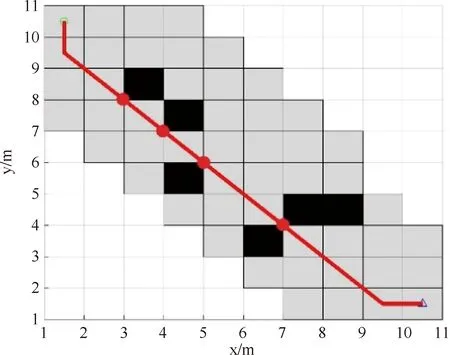
图1 传统A*算法路径规划结果图

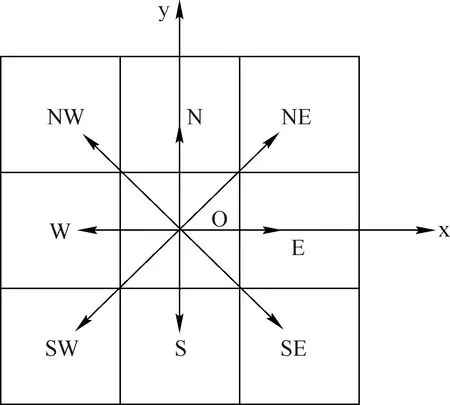
图2 邻域表示图

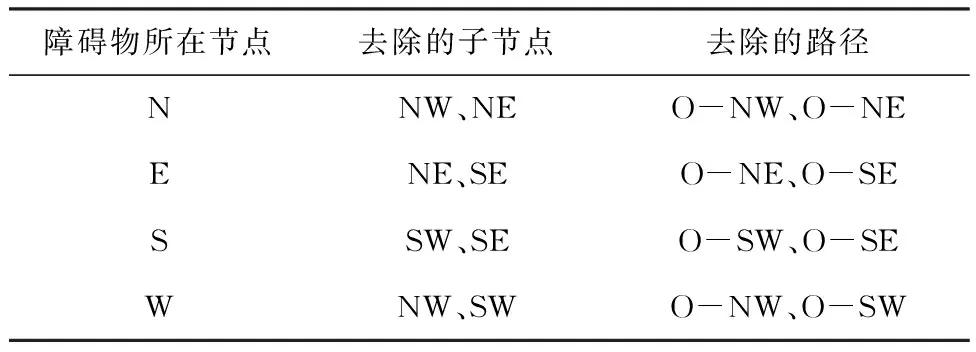
表1 普通组去除的子节点及路径

2.2 基于改进Floyd算法的轨迹优化方法

在路径的平滑性方面，随着区域内障碍物覆盖率的逐渐增加，传统A*算法规划的路径中存在较多的转折点，路径平滑性较差。因此针对此问题，本文将传统A*算法规划的路径做进一步的平滑处理，改善路径的平滑性。目前，常用的路径平滑处理算法有贝塞尔曲线以及Floyd算法等，Floyd算法作为一种基于动态规划方法的最短路径算法，又被称为插点法。在轨迹优化方面，常规的Floyd算法只进行从起始点至目标点的轨迹优化。本文采用一种基于改进Floyd算法的轨迹优化方法对路径进行平滑处理，该算法在常规Floyd算法的基础上，增加了从目标点至起始点的反向轨迹优化，采取双方向的轨迹优化方式，进一步增强路径的平滑度。除此之外，改进Floyd算法增加了碰撞距离检测，通过计算障碍物中心点与路径间的垂直距离，避免与障碍物发生碰撞。下面以图3为例，对改进Floyd算法的流程做具体阐述，其中S为起始点，T为目标点。

首先去除路径中冗余的节点，去除红色路径中除起始点S、目标点T及拐点以外的其他节点，如图3所示，去除后的路径为：S→n1→n2→n3→T。

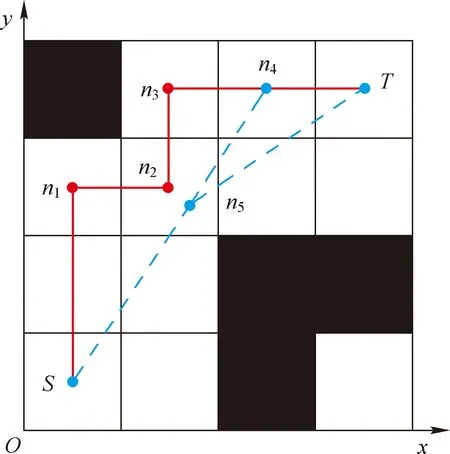
图3 改进Floyd算法示例图

然后进行正向的轨迹优化，轨迹优化阶段，设置步长为k，与障碍物安全距离为D。优化过程中，从起始点S开始，在上一步保留的路径中，相邻两个节点之间每隔k步长选取一个节点，判断选取节点与前端路径节点之间的路径是否有障碍物，并检测障碍物与路径的距离d，若d≥D，则该路径满足要求，否则不满足要求。此时，经前向轨迹优化后的路径可表示为：S→n4→T。

最后进行反向的轨迹优化，反向轨迹优化采用与正向轨迹优化相同的平滑处理方式，反向优化后路径进一步表示为：S→n5→T。

在障碍物距离检测方面，如图4所示，A、B为路径的起始点与终点，坐标分别为(xA，yA)、(xB，yB)，AB与x轴之间的夹角为α，C为障碍物中心点，坐标为(xC，yC)，点C至AB的垂直距离和纵向距离分别为d、e。因此，障碍物与路径的距离d可由A、B、C三点坐标表示为：

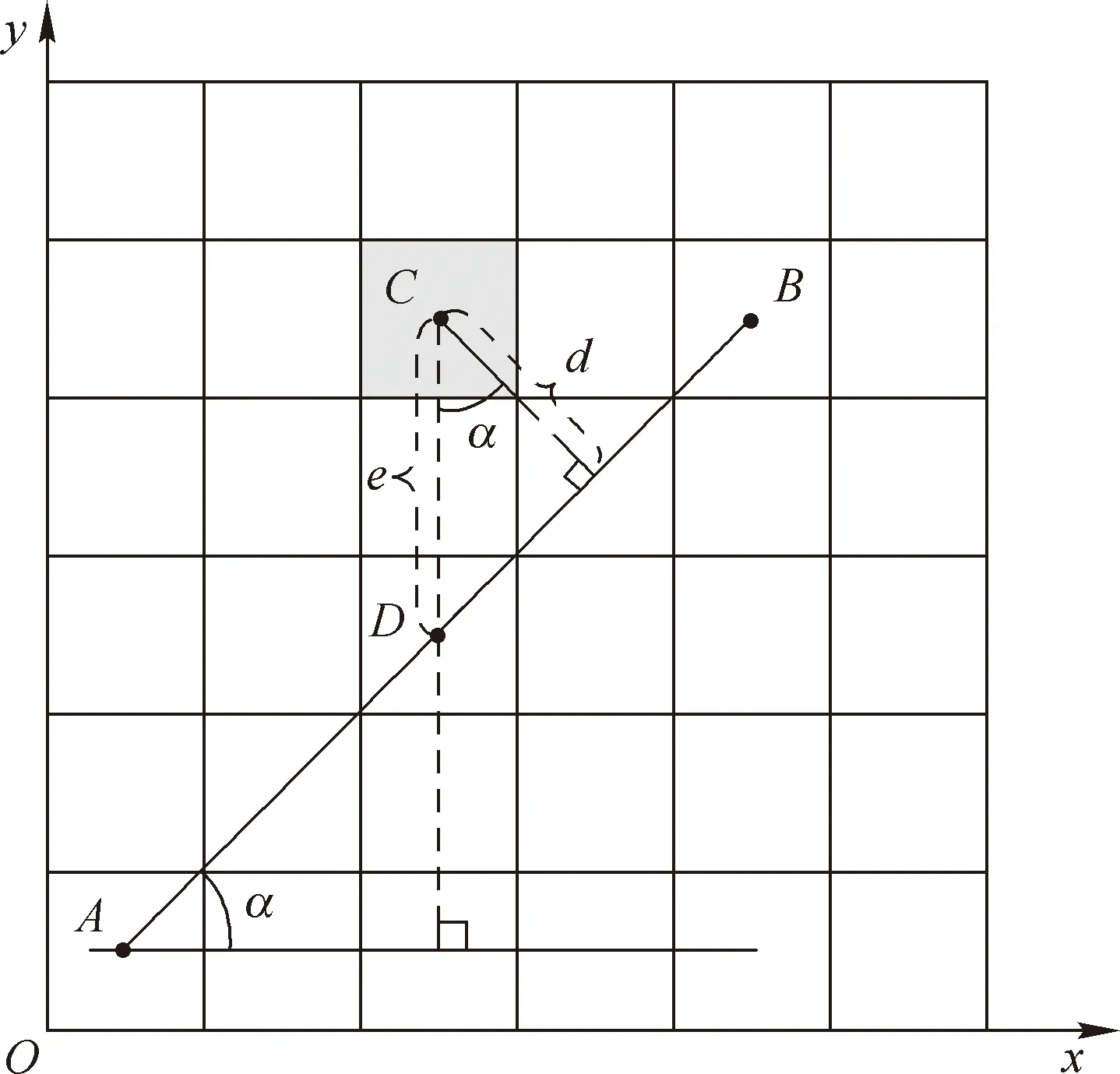
图4 障碍物距离图

d=e·cosα

(4)

其中，α、e可表示为：

(5)

(6)

根据栅格的大小，当d≥D时，表示该路径可选取，否则表示该路径不可选。

3 实验结果与分析

3.1 MATLAB仿真实验结果与分析

基于以上对改进A*算法的原理分析，本文对改进A*算法进行进一步的测试与分析，测试中使用的系统环境为Intel(R)Core(TM)i7-5500U CPU@2.40GHz Windows10专业版，软件环境为MATLAB 2019b。在障碍物覆盖率为10%、20%、30%的情况下，分别对传统A*算法、轨迹未平滑处理的改进A*算法以及轨迹平滑处理后的改进A*算法进行了测试。机器人均从左上角的起始点搜索至右下角的目标点，搜索结果分别如图5～图7所示。

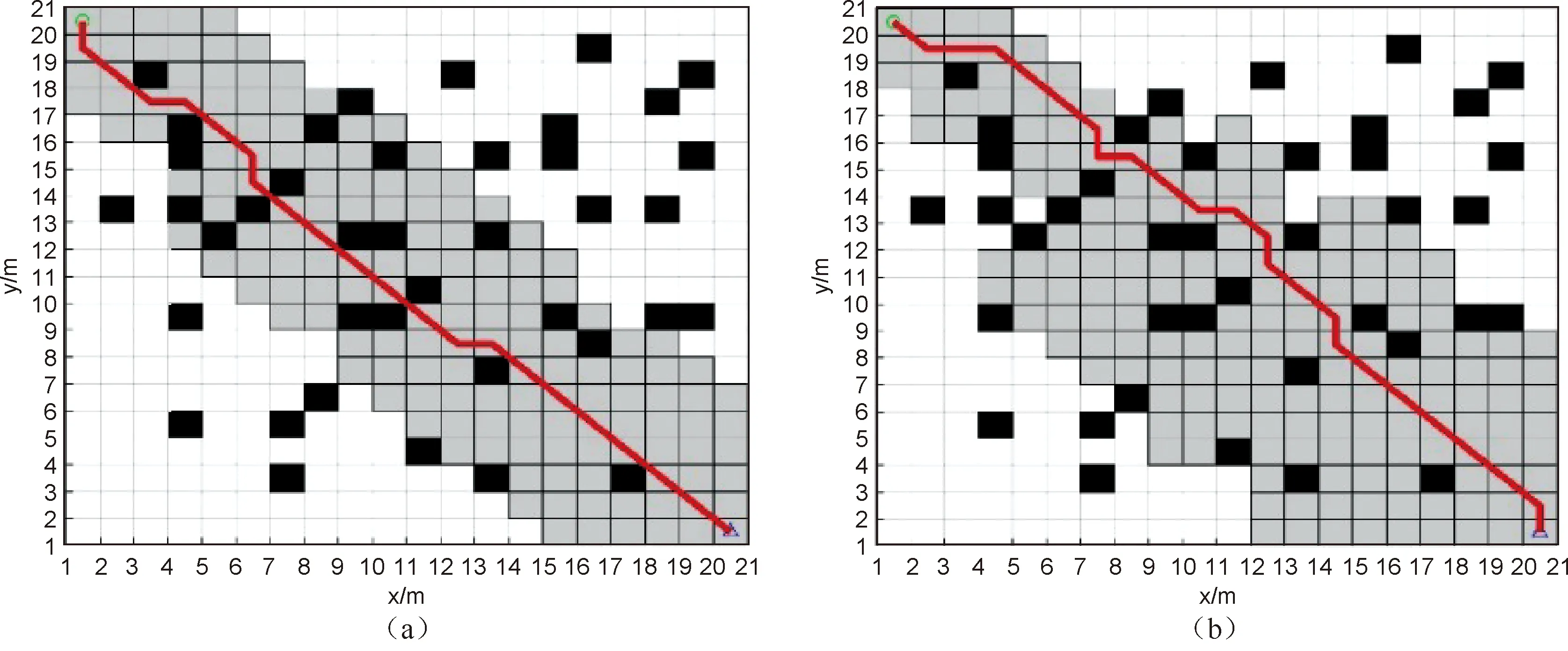
图5 仿真结果1(障碍物覆盖率10%)

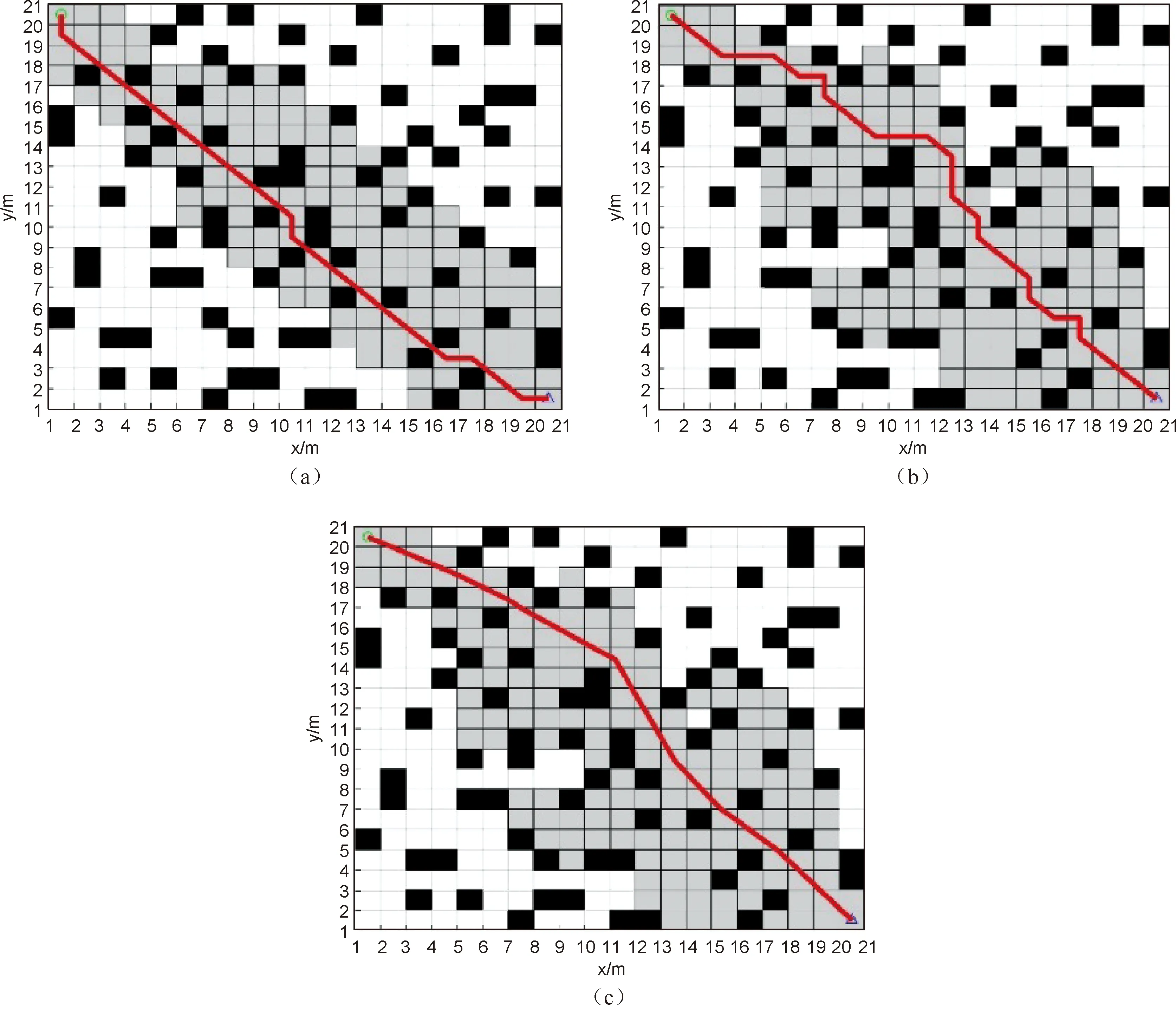
图6 仿真结果2(障碍物覆盖率20%)

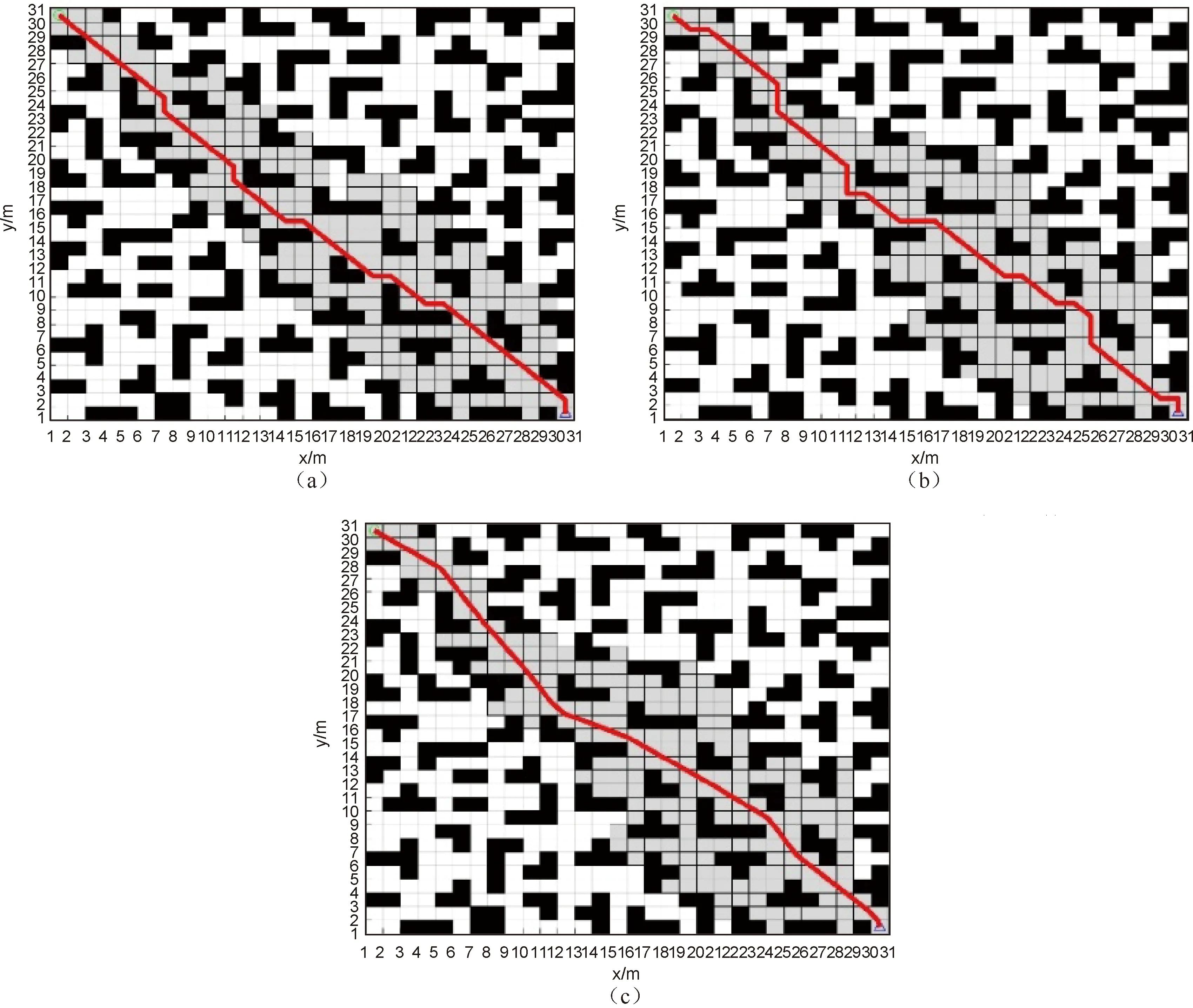
图7 仿真结果3(障碍物覆盖率30%)

从图中可以看出，三组测试均能规划出从起始点至目标点的全局路径，并且随着算法的逐步改进，路径规划的结果逐步改善，测试后的具体实验参数如表2所示。由表2可知，相比于传统A*算法，在转折点方面，每条路径中平均减少了62.49%的转折点数。在规划时间方面，平均提升了23.22%的搜索效率，在路径长度方面，平均减少了2.19%的路径长度。

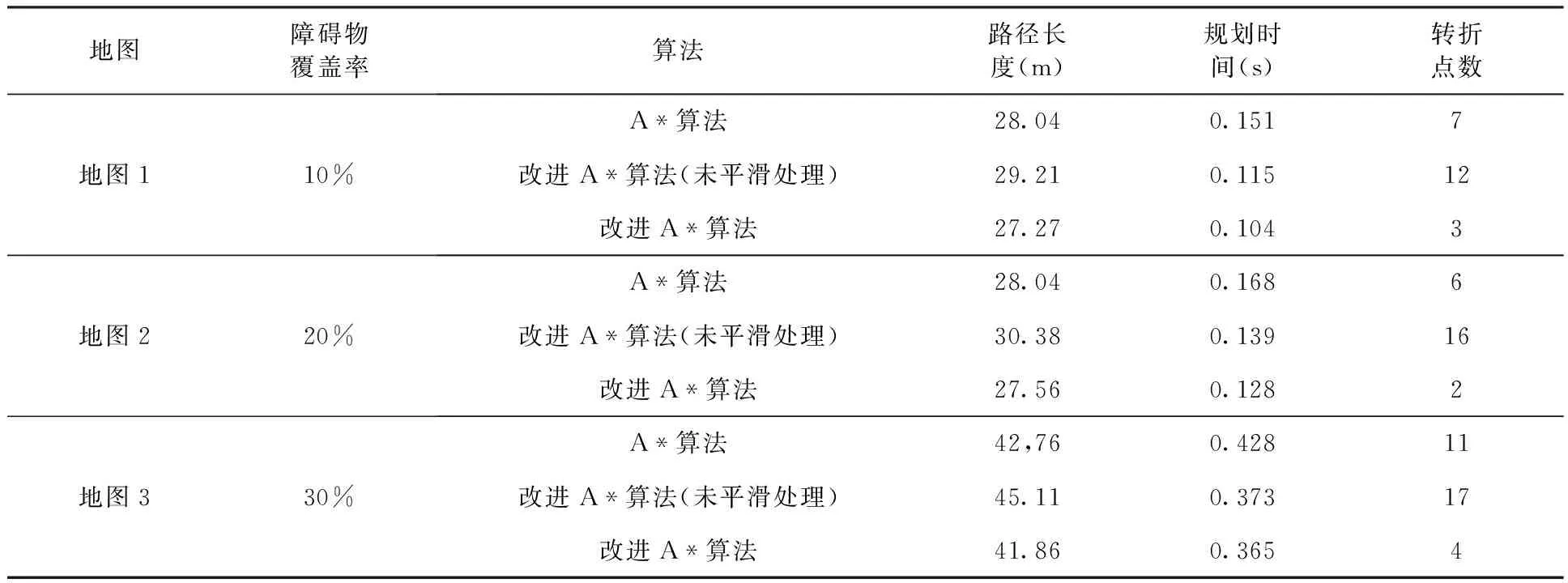
表2 具体实验参数

3.2 基于GAZEBO的室内消防救援实验结果与分析

为进一步测试改进A*算法在消防机器人中的应用效果，如图8所示。本文模拟实际的室内消防救援场景，利用GAZEBO仿真软件搭建了室内仿真环境和消防机器人模型，仿真环境整体长宽分别为30 m和20 m。结合ROS机器人操作系统，在构建完成的场景内平面栅格地图的基础上，利用Move_base导航框架，测试消防机器人消防灭火能力。

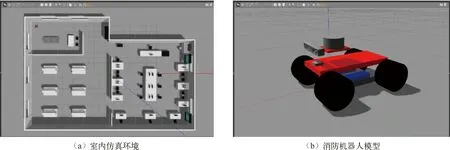
图8 室内仿真环境与消防机器人模型图

实验过程中，设定当室内发生火灾时，消防机器人从起始点开始，在指定需到达的起火点位置后，机器人便自主规划全局路径，并沿着该路径自主导航至起火点位置，及时扑灭火源，完成灭火任务。如图9、图10所示，分别为消防机器人利用传统A*算法与改进A*算法规划的全局路径。消防机器人导航过程中的相关数据见表3。

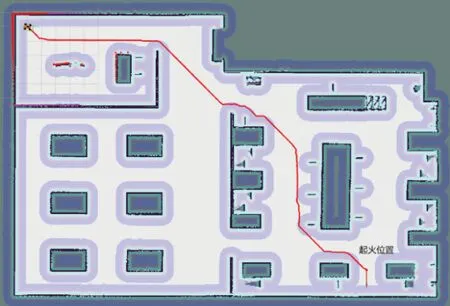
图9 传统A*算法路径规划效果图

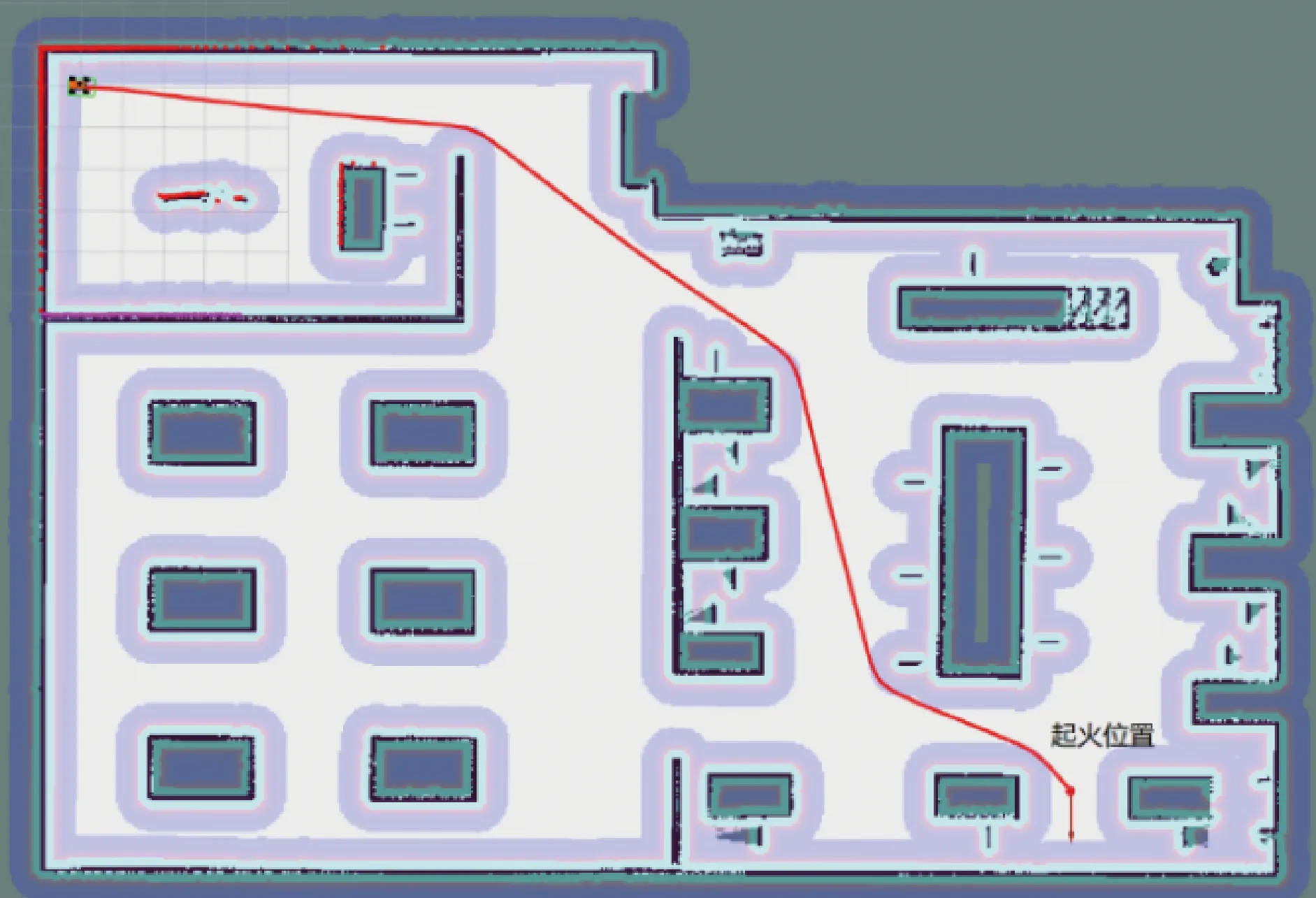
图10 改进A*算法路径规划效果图

表3 消防机器人导航相关数据

通过图表可以得出，在应用方面，改进A*算法可以较好的改善消防机器人的全局路径规划效果，并且在导航过程中，利用改进A*算法，消防机器人的整体运行速度有所提升，运行较为平稳。

4 结论

(1) 利用基于优先级的邻域搜索方式，可有效提高算法的邻域搜索效率，同时也可避免路径中出现斜穿障碍物顶点的现象，使路径规划结果更加适用于实际的消防救援场景。

(2) 利用基于改进Floyd算法的轨迹优化方法，在减少路径中的转折点数的同时，也进一步减少了路径长度，有效提高消防机器人的路径规划效率。

(3) 通过两组仿真实验，有效验证了改进A*算法的可行性以及在室内救援场景中的实用性，在此研究的基础上，未来可进一步搭建消防机器人平台，结合相关局部路径规划算法，更为全面地测试消防机器人的实际消防能力。