基于滚动轴承故障诊断的类间排斥松弛判别迁移学习

李 锋，王 腾，汤宝平，田大庆*

(1.四川大学 机械工程学院，四川 成都 610065；2.重庆大学 机械传动国家重点实验室，重庆 400044)

滚动轴承作为旋转机械中应用广泛且容易损坏的零部件，对其进行有效的故障诊断有助于预防设备事故发生。滚动轴承长期在变工况条件（如不同转速、不同负载等）下工作，一方面，这些变工况条件不但对滚动轴承的性能、可靠性有着巨大的影响，同时导致轴承新工况（当前实时的运行工况，即目标域）样本的类标签很难甚至无法获取；另一方面，正是轴承工况的多变性，造成历史工况下（辅助域）的有标签样本往往是富余的，而变工况又使得历史工况样本与新工况样本的概率分布（包括边缘概率分布和条件概率分布）存在差异。因此，仅利用历史工况下的有标签样本对滚动轴承的新工况待测样本进行故障诊断有重要的实际意义，但也有较大的挑战性。

近年来，一些学者通过支持向量机（support vector machine，SVM）、最近邻分类器（nearest neighbor classifier，NNC）、自适应增强（adaptive boosting，AdaBoost）等传统机器学习方法对变工况条件下的滚动轴承故障诊断做了一定研究，但都是基于历史工况样本和新工况样本分布一致性的假设，因此，在变工况条件下的泛化能力较差。迁移学习的主要思想是通过将辅助域中的知识迁移到目标域，来解决目标域中类标签样本匮乏下的分类问题。该方法可以缩小因变工况、不同测试环境等因素引起的数据概率分布差异，并且能够少依赖甚至不依赖新工况下的故障类标签，为变工况条件下的滚动轴承故障诊断提供了全新解决方式。现有的迁移学习方法主要有实例重加权法和特征表示法两种类型，本文研究的是特征表示法这一类迁移学习方法。现阶段，基于特征表示的迁移学习在变工况下滚动轴承故障诊断中的应用已经有了一些进展，如：康守强等将迁移成分分析方法（transfer component analysis，TCA）用于变工况下滚动轴承故障诊断；Xue等采用了一种基于混合熵特征和联合分布适配（joint distribution adaptation，JDA）相结合的方法进行变工况下滚动轴承故障模式识别；Zhang 等采用增强迁移联合匹配（enhanced transfer joint matching，Enhanced TJM）进行变工况下滚动轴承故障诊断。但上述基于特征表示的轴承故障诊断方法主要从以数据分布为中心的角度出发，旨在通过最小化公共子空间中辅助域样本与目标域样本之间的分布差异来进行迁移学习，而样本中的子空间结构和局部几何结构信息往往会被忽略。

Razzaghi等提出的低秩和判别重构矩阵迁移子空间学习（transfer subspace learning via low-rank and discriminative reconstruction matrix，TSLLRDRM）从以结构为中心的角度出发，侧重寻求一个公共子空间，使得辅助域样本和目标域样本可以很好地对齐。该方法虽然重视样本中子空间结构和局部几何结构信息，但忽略了两域样本的分布差异。本文对TSLLRDRM进行改进，提出了一种新型无监督迁移学习方法——类间排斥松弛判别迁移学习（inter-class repulsive slack discriminant transfer learning，IRSDTL）。在IRSDTL中，构造一个非负扩展松弛矩阵，将严格二进制标签矩阵转化为扩展松弛标签矩阵，从而增加辅助域中不同类标签向量之间的距离；同时，使公共子空间维数不再局限于类标签的数量，减少了原TSLLRDRM的辅助域分类误差，并提高了原TSLLRDRM的泛化能力。其次，在原TSLLRDRM基础上，引入了联合分布差异最小化两域样本分布差异，实现了以结构为中心和以数据分布为中心两种方法优势的结合，并提高了原TSLLRDRM的迁移性能。最后，构造类间排斥力项，以增加两域中某类标签子域样本到其他类标签子域样本之间的距离，进而在原TSLLRDRM基础上提高了本方法对两域样本的类判别学习能力。本文提出的IRSDTL能在新工况（目标域）样本的类标签不存在的情况下，仅利用历史工况（辅助域）中的有标签样本对目标域待测样本进行较高准确率的故障诊断。

1 类间排斥松弛判别迁移学习

在迁移学习的公共子空间中，一些潜在因素由于两域样本分布近似可被共享，因此，提出假设：在公共子空间中目标域（t）样本可由辅助域（s）样本线性表示，即：

式中：

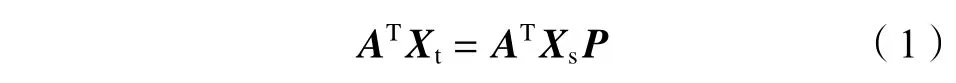
A

为映射矩阵，

A

∈R

，

m

为输入样本特征的维度，

d

为公共子空间的维度；

X

和

X

分别为输入的目标域和辅助域样本集，

X

∈R

，

X

∈R

；

P

为重构系数矩阵，

P

∈R

，

n

和

n

分别为辅助域和目标域样本的个数。由于滚动轴承辅助域和目标域样本中都存在一定环境噪声，故引入稀疏矩阵

E

来模拟这些噪声，

E

∈R。于是，式（1）可进一步表示为：

通过对重构系数矩阵

P

施加低秩和稀疏约束，以保留样本的全局子空间结构和局部几何结构的信息，使两域样本在公共子空间具有相似的几何性质；并对噪声矩阵

E

施加稀疏约束，以初步减轻噪声带来的影响。由于秩最小化问题是非凸的，一般将秩约束问题用核范数代替，则IRSDTL的初始目标函数可表示为：

式中： ||·||表 示矩阵的核范数，用于代替低秩约束；λ和 β为权重参数，用于控制不同项的影响；| |·||表示矩阵的1范数，用于表示稀疏约束。

1.1 非负扩展松弛矩阵

由于环境噪音干扰，在历史工况（辅助域）下所提取的滚动轴承状态特征样本往往存在交叉、混叠现象，造成样本可区分性差。因此，构造非负扩展松弛矩阵来增大映射后辅助域不同类别特征样本间距离，增大滚动轴承历史工况下不同类别样本间的区分性，进而减少辅助域分类误差。定义一个判别学习函数 φ (

A

,

Y

,

X

)：

式中：

Y

为扩展二进制标签矩阵，

Y

∈R，由已知的辅助域二进制标签矩阵

Y

扩展而来，

Y

∈R（

C

为标签类别的总数目），即在

Y

中所有的单个二进制标签向量

y

后增加（

d

−

C

）个 “0”，可得

Y

； α为正则化参数； | |·||表 示矩阵的F范数；

Y

+

B

⊙

K

为扩展松弛标签矩阵。

Y

+

B

⊙

K

中， ⊙ 为Hadamard积算子；

K

为非负扩展松弛矩阵，

K

∈R，

K

为

K

的元素，为极小的正数；

B

为矩阵，若

Y

=1， 则

B

=1， 若

Y

=0 ，则

B

=−1。在判别学习函数 φ(

A

,

Y

,

X

)中，通过扩展二进制标签矩阵使得公共子空间维度不再局限于标签类别的数目，进而使得降维维度从特殊到一般。在此基础上，为进一步增加不同类别样本间的区分性，构造非负扩展松弛矩阵

K

，获得的扩展松弛标签矩阵

Y

+

B

⊙

K

中不同类标签向量之间的距离大于原有扩展二进制标签矩阵

Y

中不同类标签向量之间的距离。将严格二进制标签矩阵转化为扩展松弛标签矩阵后，样本更具区分性，降低了辅助域分类误差。联合式（3）、（4），IRSDTL的目标函数更新为：

1.2 联合分布差异

由于滚动轴承长期在变工况条件下工作，这些变工况条件使得历史工况下的样本与新工况下的样本的分布差异较大。为此，引入联合分布差异来最小化辅助域和目标域样本分布差异，以更好地实现从辅助域向目标域的跨域迁移。联合分布差异由边缘分布差异

D

(

D

,

D

)及 条件分布差异

D

(

D

,

D

)组成，表达式分别为：

式中：

D

表示辅助域；

D

表示目标域；

D

表示辅助域第

c

类样本的子域；

D

表示目标域第

c

类样本的子域；

n

表示辅助域第

c

类样本的数目；

n

表示目标域第

c

类样本的数目；

x

和

x

分别表示辅助域和目标域中任意一个样本；

X

为目标域和辅助域样本组成的集合，

X

=[XsXt]∈Rm×n ；N0为边缘分布的最大均值差异（maximum mean discrepancy，MMD）矩阵；

N

为第

c

类样本的条件分布的最大均值差异矩阵。

N

、

N

的计算式分别为：

联立式（6）和（7），则可得联合分布差异

Dist

，其表达式为：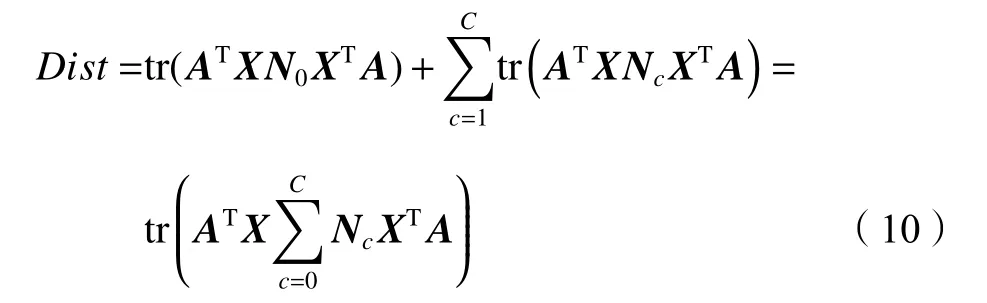

式中， t r(·)表 示矩阵的迹，

C

表示样本类别的总数目。于是，可以通过最小化联合分布差异

Dist

来减小两域样本的分布差异。将式（10）并入式（5），则IRSDTL的目标函数更新为：

式中， σ为权重参数。

1.3 类间排斥力项

虽然减小联合分布差异能够缩小辅助域和目标域中滚动轴承状态特征样本的分布差异，但由于在两域中都存在环境噪声干扰，因此两域中所提取的滚动轴承特征样本都存在交叉、混叠现象，致使映射后两域中不同类标签子域样本的判别性仍有不足。为此，构造类间排斥力项来增加滚动轴承在两域中某类标签子域样本到其他类标签子域样本之间的距离，进一步提高对两域样本的类判别学习能力。类间排斥力项

M

表达式为：

式中，

M

、

M

、

M

、

M

分别表示 辅 助 域 样 本 到 辅助域样本、辅助域样本到目标域样本、目标域样本到辅助域样本和目标域样本到目标域样本的散布矩阵。以散布矩阵

M

和

M

为例，计算式分别为：

式中，

r

表示除第

c

类外的其他类别，

D

和

n

分别表示目标域样本中除第

c

类外的其他类别的样本集及其数目。其余两种散布矩阵

M

和

M

的计算式与式（13）和（14）类似。通过两域间的散布矩阵可以计算出不同类标签子域样本的距离，以散布矩阵

M

为例，可以通过式（15）得到辅助域中类别为

c

的样本到目标域中其他类别（除类别

c

外）样本的距离之和

D

：

D

、

D

和

D

的计算公式与式（15）类似，分别可通过散布矩阵

M

、

M

、

M

计算得到。在式（12）和（15）的基础上计算

D

、

D

、

D

和

D

之和，可推导出最大化类间距离的表达式为：

将式（16）并入式（11）中，则IRSDTL的目标函数更新为：

式中， σ为权重参数。

1.4 IRSDTL整体框架（IRSDTL参数）的优化

由于式（17）是非凸的，通过添加两个辅助变量

P

、

P

来放松原始问题。则式（17）转换为：

将式（18）借助增广拉格朗日乘子法转化为一个无约束问题，如式（19）所示：

式中：

Y

、

Y

和

Y

均为拉格朗日乘子，

Y

∈R

，

Y

∈R，

Y

∈R；µ(µ>0)为惩罚参数。采用交替方向乘子法求解式（19）的步骤如下：1）首先更新

A

，这一步所需解决的优化问题为：

式（20）求解结果为：

式中，

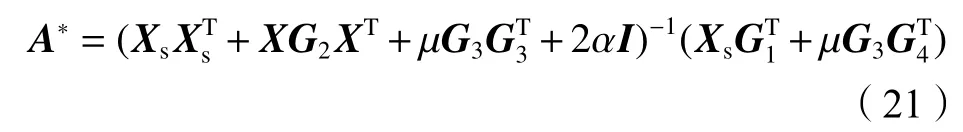
A

为

A

的局 部 最优 解，

G

=

Y

+

B

⊙

K

,

G

=2）其次更新

P

，求解如下函数：

式（22）封闭形式的解为：

式中，

P

为

P

的局部最优解，3）更新

P

和

E

，需分别解决优化问题如下：

式中，

P

为

P

的 局部最优解，

E

为

E

的局部最优解。使用软阈值函数得到式（24）和（25）求解结果，分别为：

式中， s oft(

z

,

a

)=sign(

z

)max(|

z

|−

a

,0)。4）更新

P

，求解如下函数：

式中，

P

为

P

的局部最优解。

使用奇异值阈值（singular value thresholding，SVT）求解式（28），结果为：

式中，

U

和

V

分别表示对

G

进行奇异值分解得到的正交矩阵，为软阈值操作，为

G

奇异值的，

r

为

G

的秩。5）更新

K

，求解如下函数：

式中，

K

为

K

的局部最优解。令

R

=

A

X

−

Y

，则式（30）的结果为：

最后，拉格朗日乘子

Y

、

Y

、

Y

及 惩罚参数 µ通过式（32）更新：

式中， ρ （ ρ>1）为迭代步长。

通过式（20）～（32），不断迭代更新

A

、

P

、

K

等矩阵，最终输出优化后的映射矩阵

A

。通过优化后的映射矩阵

A

，得到降维后的辅助域低维训练特征样本集

Z

和 目标域低维待测特征样本集

Z

， 其表达式分别为：

2 基于IRSDTL的滚动轴承故障诊断方法

图1描述了所提出的基于IRSDTL的滚动轴承故障诊断方法的实现过程。该过程主要包括4个步骤：1）从历史工况（含标签）和新工况（不含标签）的滚动轴承的状态信号中，提取时域和频域特征，并采用集成经验模态分解（ensemble empirical mode decomposition，EEMD）提取时频域特征；然后，将以上时域、频域和时频域特征归一化处理，构成原始维度为

m

（

m

=27）的辅助域和目标域的状态特征样本集。2）将辅助域样本集及其类标签和目标域待测样本集输入IRSDTL中，通过优化IRSDTL整体迁移学习框架的方式获得优化后的映射矩阵

A

；然后，将原始两域样本映射到公共子空间中，分别得到辅助域训练样本和目标域待测样本的低维特征向量

z

（

z

∈

Z

），

z

（

z

∈

Z

）。3）将辅助域训练样本的低维特征向量及其类标签输入到最小二乘支持向量机（least squares support vector machine，LSSVM）中以建立LSSVM的分类训练模型。4）将目标域待测样本输入训练好的LSSVM模型中，完成待测样本类标签的判别，实现故障诊断。

图1 基于IRSDTL的滚动轴承故障诊断方法的实现过程Fig. 1 Implementation of the IRSDTL-based fault diagnosis method for rolling bearings

3 实验分析

3.1 实验装置

表1给出了本文所使用的滚动轴承故障实验数据的信息，包括滚动轴承实验数据的来源及实验工况（滚动轴承的转速和所传递的功率或所受径向载荷）。

表1 实验工况
Tab. 1 Detailed working conditions

数据来源 工况 转速/(r·min-1) 功率/kW 径向载荷/lbs C1 1 772 0.74 —C2 1 730 2.22 —C3 1 750 1.48 —辛辛那提大学 C4 2 000 — 6 000凯斯西储大学

如表1所示，本文所使用的部分实验数据来自凯斯西储大学电气工程实验室滚动轴承数据中心，实验平台如图2所示。采用该实验平台驱动端滚动轴承（型号为SKF6205-2RS）振动加速度数据作为实验数据。该实验室利用电火花加工的方式在3个驱动端滚动轴承的内圈、外圈和滚动体上分别加工直径为0.335 6 mm，深度为0.279 mm的小槽，模拟内圈、外圈和滚动体单点点蚀（断裂）故障。用信号采集仪以12 kHz的采样频率，采集C1、C2和C3（表1）3种工况下滚动轴承的振动加速度信号。截取每512个连续的振动加速度数据点作为1个样本。采集每种工况下，内圈点蚀故障、外圈点蚀故障、滚动体点蚀故障及正常状态的样本各220个，也就是说每种工况下共有220×4个样本。

图2 凯斯西储大学滚动轴承故障模拟实验平台Fig. 2 Fault simulation experimental platform of rolling bearings in Case Western Reserve University

另外，表1中C4工况的实验数据来自辛辛那提大学的滚动轴承测试，实验平台如图3所示。该实验室将4个ZA-2 115双列滚子轴承安装在轴承试验台的旋转轴上，使用转速为2 000 r/min的电机通过皮带驱动转轴，并利用弹簧机构在旋转轴和轴承上施加6 000 lbs的径向载荷。以20 kHz的采样频率采集故障期间的振动加速度数据点，并截取每512个连续点作为1个样本。与C1、C2和C3工况下数据点相似，C4工况下，采集到内圈故障、外圈故障、滚动体故障以及正常状态的样本均为220个，即C4工况下共采集220×4个样本。

图3 辛辛那提大学滚动轴承故障实验台Fig. 3 Accelerated rolling bearing life cycle degradation test platform in University of Cincinnati

为了更真实地模拟工业现场环境，对表1中所有工况下的全部故障的振动加速度数据加入高斯白噪声，使这些数据的信噪比为-2 dB。

3.2 基于IRSDTL的故障诊断方法参数设置

IRSDTL参数设置如下：正则化项权重参数α=0.3； 重 构系数矩 阵

P

的权重 参 数 λ =0.2 ；噪声 矩 阵

E

的权重参数 β=0.01； 联合分布差异项权重参数σ=0.1； 类间排斥力项权重参数σ=0.3； 映射矩阵

A

的映射维度

d

=5； 迭代步数

T

=20。IRSDTL中其余无需人工设置的参数初始化如下： ρ=1.01， µ=0.02 ， µ=10，

E

=0，

K

=1，

M

=0，

Y

=

Y

=

Y

=0，

P

=

P

=

P

=0。在LSSVM分类器中，正则化参数 δ =4 ，核参数θ =1。参数设置好后在本文所有实验中保持不变。

3.3 实验结果

1）实验1

实验1中，将C1工况下的样本作为辅助域有标签样本，将C3工况下的样本作为目标域无标签样本用于方法测试。实验之前，辅助域用作训练样本的有标签样本和目标域中用作训练样本的无标签样本数量均取为 2 20×4（4表示4种状态类型：正常状态+3种故障），这意味着目标域中所有无标签样本均参与训练IRSDTL（优化IRSDTL的框架，即优化IRSDTL的参数）。然后，将所提出方法和其他4种迁移学习方法（JDA、TJM、联合几何和统计对齐（joint geometrical and statistical alignment，JGSA）、TSLLRDRM）得到的诊断准确率进行比较（被用来对比的4种迁移学习方法所采用的特征提取方式和分类器均与所提出的基于IRSDTL的故障诊断方法相同）。表2为5种方法对目标域待测样本的故障诊断准确率和平均故障诊断准确率。

表2 实验1中5种迁移学习方法对测试集的故障诊断准确率
Tab. 2 Fault diagnosis accuracy rates of five transfer learning-based methods on the testing sample set in Experiment 1

不同状态下的故障诊断准确率 /% 平均诊断准确率/%内圈故障 外圈故障 滚动体故障 正常状态基于IRSDTL的方法 94.55 100.00 95.00 100.00 97.39基于JDA的方法 68.18 85.00 60.45 85.45 74.77基于TJM的方法 75.91 86.82 65.45 95.91 81.02基于JGSA的方法 80.91 91.82 81.36 98.18 88.07基于TSLLRDRM的方法 94.09 86.36 81.82 93.64 88.98方法

同时，为了直观地验证IRSDTL迁移和分类的有效性，利用t-分布随机邻域嵌入（t-distributed stochastic neighbor embedding，t-SNE）算法将IRSDTL公共子空间中的5维特征降维到2维平面，并以散点图形式呈现，如图4所示。

由图4可知，对在IRSDTL公共子空间中的辅助域5维训练特征样本集和目标域5维待测特征样本集进行降维后，相同状态（相同类别）样本较好地聚合在一起，且不同状态（不同类别）样本之间相对较为分散，其原因是：IRSDTL在保证辅助域和目标域样本全局子空间结构和局部几何结构较好对齐的前提下，减少了两域样本分布差异，同时增大了两域不同类别样本之间距离，从而提高了方法的迁移性能和类判别能力。因此，所提出的基于IRSDTL的故障诊断方法具有比其他4种迁移学习方法更高的故障诊断准确率，如表2所示。此外，所提出的故障诊断方法将内圈故障、外圈故障和滚动体故障误诊为正常状态的误诊率分别为0、0、0.45%；将正常状态误诊为内圈故障、外圈故障和滚动体故障的误诊率均为0，说明该方法一定程度上能有效避免无法发现故障或故障误报的情况。

图4 IRSDTL公共子空间中的5维特征经t-SNE降维后的散点图Fig. 4 Scatter plot of 5-dimension features in the common subspace of IRSDTL after dimension reduction by t-SNE

2）实验2

实验2中，将C2工况下的样本作为辅助域有标签样本，将C3工况下的样本作为目标域无标签样本用于方法测试。实验过程与实验1类似，比较了所提出的方法和其他4种迁移学习方法所得到的故障诊断准确率（表3）；并利用t-SNE算法将IRSDTL公共子空间中的5维特征降维到2维平面，其散点结果如图5所示。

图5的结果与图4类似，对在IRSDTL公共子空间中的辅助域5维训练特征样本集和目标域5维待测特征样本集降维后，两域中4种状态（3种故障状态和正常状态）的相同状态样本较好地聚合在一起，而不同状态样本之间相对较为分散。该可视化结果表明，在以C2工况下的样本作为辅助域有标签样本，以C3工况下的样本作为目标域无标签样本的条件下，IRSDTL仍然具有较好的迁移性和分类性。因此，基于IRSDTL的故障诊断方法具有比其他4种迁移学习方法更高的故障诊断准确率，这在表3所展示的对比结果中得到了印证。另外，本文方法将3种故障状态误诊为正常状态的误诊率都为0，而将正常状态误诊为3种故障状态的误诊率也都0，进一步说明该方法能有效避免无法发现故障或故障误报的情况。

表3 实验2中5种迁移学习方法对测试集的故障诊断准确率
Tab. 3 Fault diagnosis accuracy rates of five transfer learning-based methods on the testing sample set in Experiment 2

方法 不同状态下的故障诊断准确率/% 平均诊断准确率/%内圈故障 外圈故障 滚动体故障 正常状态基于IRSDTL的方法 76.36 100.00 88.18 100.00 91.14基于JDA的方法 70.00 63.18 55.45 86.36 68.75基于TJM的方法 67.27 85.91 70.45 98.18 80.45基于JGSA的方法 63.18 92.73 83.18 95.91 83.75基于TSLLRDRM的方法 73.64 96.36 74.55 100.00 86.14

图5 IRSDTL公共子空间中的5维特征经t-SNE降维后的散点图Fig. 5 Scatter plot of 5-dimension features in the common subspace of IRSDTL after dimension reduction by t-SNE

3）实验3

实验3中，将C1、C2和C3工况下样本混合作为辅助域有标签样本，将C4工况下样本作为目标域无标签样本用作测试。具体而言，将C1工况下的 7 0×4（对每种状态从原有的220个样本中随机选取70个，下文同）个有标签样本、C2工况下的 70×4个有标签样本和C3工况下的 80×4个有标签样本混合作为辅助域中的训练样本（共 2 20×4）；同时，将C4工况下的无标签样本作为目标域当前待测样本，其数量为 220×4，且这些当前待测样本均参与训练IRSDTL。将所提出方法对滚动轴承ZA-2 115的4种状态下当前待测样本的诊断准确率及平均诊断准确率与其他4种迁移学习方法进行了比较，结果如表4所示；同时利用t-SNE算法将IRSDTL公共子空间中的5维特征降维到2维平面，其散点结果如图6所示。

图6 IRSDTL公共子空间中的5维特征经t-SNE降维后的散点图Fig. 6 Scatter plot of 5-dimension features in the common subspace of IRSDTL after dimension reduction by t-SNE

表4 实验3中5种迁移学习方法对测试集的故障诊断准确率
Tab. 4 Fault diagnosis accuracy rates of five transfer learning-based methods on the testing sample set in Experiment 3

方法 不同状态下的故障诊断准确率/% 平均诊断准确率/%内圈故障 外圈故障 滚动体故障 正常状态基于IRSDTL的方法 97.73 100.00 90.91 100.00 97.16基于JDA的方法 71.82 57.27 65.45 45.91 60.11基于TJM的方法 54.55 98.64 58.18 72.73 71.02基于JGSA的方法 62.73 94.09 80.00 98.64 83.86基于TSLLRDRM的方法 78.64 91.82 81.36 100.00 87.95

由图6可视化结果可知，在将C1、C2和C3工况下样本混合作为辅助域有标签样本，以C4工况下样本作为目标域无标签样本的条件下，IRSDTL仍然具有较好的迁移性和分类性。因此，基于IRSDTL的故障诊断方法仍然具有比其他4种迁移学习方法更高的故障诊断准确率。另外，在实验中，所提出的方法将3种故障状态误诊为正常状态的误诊率均为0，将正常状态误诊为3种故障状态的误诊率也均为0，说明该方法能有效避免无法发现故障或故障误报的情况。

3.4 所提出方法的鲁棒性分析

为验证本文方法的鲁棒性，将实验1、2和3中的辅助域有标签样本分别作为实验4、5和6的辅助域训练样本集，同时从实验1、2和3的目标域无标签样本中按比例随机选样，分别作为实验4、5和6的目标域待测样本集。实验4、5、6中，在增大辅助域训练样本数量与目标域待测样本数量的比值

g

（只减少目标域中无标签训练样本的数量）的条件下，将所提出的基于IRSDTL的故障诊断方法的平均诊断准确率与其他4种迁移学习方法进行了比较，结果如图7所示。

由图7可知，相比其他4种迁移学习方法，所提出故障诊断方法对目标域无标签训练样本数量具有更好的鲁棒性。随着目标域训练样本数量的减少，其平均故障诊断准确率波动相对最小、更为平稳且整体上高于其他4种迁移学习方法。因此，IRSDTL对目标域样本依赖程度相对较低，在目标域待测样本（待测样本均参与了训练IRSDTL）数量较少的情况下，仍能较平稳地实现从辅助域向目标域的跨域迁移和类判别，目标域样本的数量对基于IRSDTL的故障诊断方法的故障诊断准确率影响较小。

图7 在不同辅助域和目标域样本数比值 g 下，5种迁移学习方法的平均诊断准确率对比Fig. 7 Comparison of the average diagnosis accuracy of the five transfer learning-based methods with differentg

4 结 论

1）所提出的基于IRSDTL的故障诊断方法在已有的TSLLRDRM基础上，构造一个非负扩展松弛矩阵，将严格二进制标签矩阵转化为扩展松弛标签矩阵，增加辅助域中不同类标签向量之间的距离，同时使公共子空间维数不再局限于类标签的数量，减少了TSLLRDRM的辅助域分类误差，并提高了TSLLRDRM的泛化能力。

2）IRSDTL引入了联合分布差异，从而将以结构为中心和以数据分布为中心两种方法的优势结合了起来，既重视样本的结构信息，又关注样本的分布差异，提高了原TSLLRDRM的迁移能力；同时，构造了类间排斥力项，增加两域中某类标签子域样本到其他类标签子域样本之间的距离，提高了TSLLRDRM对两域样本的类判别性能。

3）采用交替方向乘子法优化IRSDTL的整体框架，以放宽IRSDTL的目标函数的凸限制，从而便捷地得到IRSDTL参数的最优解。

4）IRSDTL的以上优势使得IRSDTL从辅助域向目标域跨域迁移学习时具有更好的迁移性能和分类准确率。因此，该方法在新工况样本的类标签不存在情况下，仅利用历史工况中的有标签样本就能对新工况待测样本进行更准确和较好鲁棒性的故障诊断。