如何求不规则阴影图形的面积
顾杰超
求阴影部分图形的面积是一类常见的问题,但题目中的阴影部分常常不是以规则的形状出现,而是由一些基本图形组合、拼凑而成的.它们的面积无法直接利用公式计算,一般我们称这样的图形为不规则图形.对于这类不规则阴影图形的面积,我们可根据图形的特点,将它们分解、转化成我们所熟悉的规则图形来求解,但在转化的过程中方法是多种多样的.现介绍几种常用的方法.
一、利用平移法求解
平移法是求解不规则阴影图形面积的一种常用方法.它是指通过对图形的平移,使图形的位置发生改变,从而使不规则图形转化为规则图形,进而达到轻松求解的目的.
例1如图1,两个半圆中,小圆的圆心O’在大⊙O的直径CD上,长为4的弦AB与直径CD平行且与小半圆相切,那么圆中阴影部分的面积等于.

分析:通过仔细观察,可以看出,较小的半圆是夹在弦AB与直径CD这两条平行线之间的,如果把较小的半圆沿着直径CD向右平移,使圆心O’与较大的半圆的圆心O重合,小半圆的面积不变,因而阴影部分的面积未变.连接OB,作OP⊥AB于点P,用大半圆的面积减去小半圆的面积即可得到阴影部分的面积.
解:把较小的半圆向右平移,使其圆心O’与较大的半圆的圆心O重合,可知切点P即为弦AB的中点,再连接OB,过圆心O作OP⊥AB于点P,就可以得到Rt△PBO,如图2.

评注:本题通过小半圆的平移,使圆心O1与大半圆的圆心O重合,将一个不易求解的不规则图形面积转化为两个规则图形的面积差.
二、利用旋转法求解
旋转法是指按照顺时针或逆时针的方向,将图形的某部分绕着某一定点旋转适当的角度,使已知图形与所求图形之间能够建立起某种联系,从而找到解题的突破口.



评注:本题利用图形的特点,将图中某一部分图形进行旋转后把阴影部分组合为一个规则的图形,然后利用面积公式求解.
三、利用割补法求解
割补法是指通过对几何图形进行合理的分割和添补,把不规则、不熟悉、复杂的几何图形变为规则、熟悉、简单的几何图形.它是求不规则阴影图形面积的有效方法之一.
例3如图5,正方形ABCD边长为2,两对角线交点为O,OEFG也为正方形,则图中阴影部分面积为.
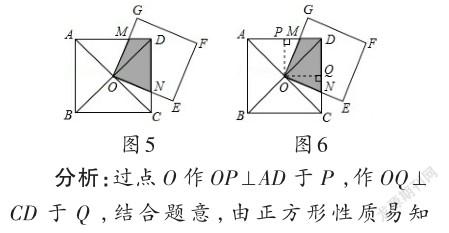

故答案為:1.
评注:本题运用了正方形性质和三角形全等的知识.通过将△QON割补到△POM的位置,把阴影图形的面积转化为规则图形的面积,从而便于求解.
综上所述,不管是平移法、旋转法,还是割补法,其实质都是通过图形的位置变换,化不规则为规则,化陌生为熟悉,化繁难为容易,从而顺利解题.同学们在求解不规则阴影图形的面积时,要注意从题设出发,结合图形特征,灵活运用这些方法,有效破解难题.

