关于数学课堂“动手做”的实践与思考

江苏灌云县下车中心小学（222200）赵云康

“动手做”专题是苏教版教材的特色之一，学习内容与单元教学内容相契合，一般以一道题的形式呈现，让学生通过动手做一做，探究问题规律、原理等。笔者认为，“动手做”只有与思考结合起来，才能让学生掌握获得数学知识的方法，使学生由不会到会，一步步抵达问题的核心，直至解决问题。那么，在“动手做”的过程中，怎样才能把“做”与“思”结合起来，实现“做思互促，做思共生”，帮助学生搭建起实践与思维的桥梁呢？

一、凸显“思”的自由

“动手做”不仅要动手，还要动眼、动脑。从这个意义上来看，“动手做”属于数学学习的一体两面。在教学时，教师要通过做来促进学生思考，再通过思考来引领学生做，让学生在做中体验数学的魅力。因此，“做”的过程也是思考的过程。

以苏教版教材二年级上册“厘米和米”单元编排的“动手做”为例（如图1）。

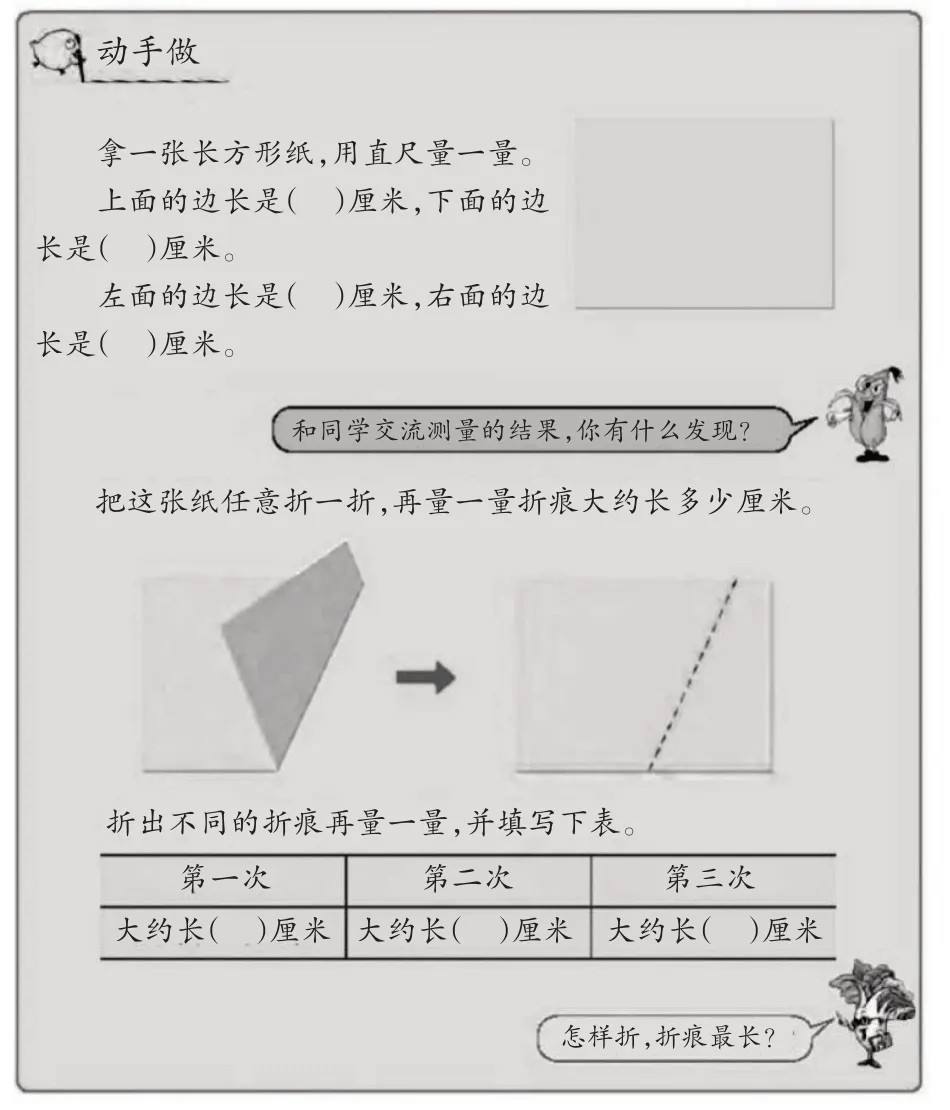
图1

这次“动手做”主要围绕本单元的“线段”和“测量长度”内容而编排的，“动手做”的训练内容包括两个方面：一是测量长方形纸四条边的长度，二是测量长方形纸折痕的长度。

活动要求：

1.学生学会使用直尺，并用学到的测量方法量长度，说说长方形纸的每条边长是多少。

2.学生自由测量，交流自己的测量结果。

3.每名学生至少测量3次不同折痕的长度，体会不同线段的长度可能不同，并思考怎样折，折痕才是最长的。

4.学生汇报测量结果。

在学生动手测量的时候，教师只是提醒学生要用正确的测量方法进行测量，而对于学生想怎样测量，教师并没有强加干涉，这就为学生提供了自主思考和操作的机会。在这个“动手做”的过程中，学生放开手脚去测量，不仅得出了长方形纸边长的正确数据，而且在反复测量长方形纸不同折痕的过程中对“长方形的对角线在所有折痕中是最长的”认识也更加深刻。

二、明确“思”的路径

在数学教学中，对于要研究的问题，教师通常按照“提出问题—构建概念—寻找方法—提出假设—验证猜想—语言表述”的步骤来引导学生解题。在“动手做”教学中，教师要让学生在做中思考，以帮助学生发现解决数学问题的普遍规律，让学生由“会解一道题”变成“会解一类题”。

以苏教版教材一年级下册“认识图形”单元编排的“动手做”为例（如图2）。

图2

这次的“动手做”是让学生进行拼图，教材的附属页里有4个蓝色的正方形、4个黄色的圆形、4个绿色的长方形和8个红色的三角形，学生可以把这些图形剪下来拼成美丽的图案。

这次“动手做”可以分两次活动来进行。

活动一：学生拿出剪下来的图形照着教材中的图案拼。

活动二：学生自由拼图案。有了活动一的拼图经验，学生这次要发挥想象力去拼，拼完以后互相交流（自己拼的图案像什么，分别用了哪些图形，每种图形各用了几个）。

学生汇报如下。

生1：我拼的是小房子，用了2个三角形、2个正方形。

生2：我拼的是大树，用了2个三角形、1个长方形。

生3：我拼的是小汽车，用了2个三角形、2个圆、1个正方形。

……

在拼图的过程中，学生一是模仿，二是创造。模仿时需要思考教材中的图案是怎样拼的，这样才能掌握拼的方法。而创造需要想象力，更需要思考怎样才能创造出属于自己的个性图案，这样就可以使学生的想象力与创造力得到有效发展。

三、关注“思”的层次

传统的数学教学一般是由复习引入、探索新知、巩固练习、总结反思等环节组成，以使学生对所学知识的印象更深刻。在“动手做”的课堂中，教师可采用问题使做的形式贯穿整节课，为学生提供独立思考的机会，让学生的做显得更有层次。

以苏教版教材三年级下册“年、月、日”单元编排的“动手做”为例（如图3）。

图3

这次“动手做”的内容是让学生在用长方形框数的过程中发现相邻的数之间的关系，以此激发学生探究年、月、日的欲望。

问题一：用长方形横着框出3个数，这3个数之间有什么关系？

学生的答案：（1）框出的数是16、17、18，16+17+18=51，51÷3=17，16+18=34，34÷17=2；（2）框出的数是4、5、6，4+5+6=15，15÷3=5，4+6=10，10÷5=2……

学生汇报交流：框出的3个数为连续的自然数，后一个数比前一个数多1，中间的数是这3个数的平均数，第一个数和第三个数之和是中间的数的2倍。

问题二：用长方形竖着框出3个数，可以怎样框？框出的数之间有什么关系？

学生的答案：（1）框出的数是7、14、21，7+14+21=42，42÷3=14，7+21=28，28÷14=2；（2）框出的数是8、15、22，8+15+22=45，45÷3=15，8+22=30，30÷15=2……

学生汇报交流：竖着框出的3个数，下一个数比上一个数多7，中间的数是这3个数的平均数，上下两个数之和是中间的数的2倍。

问题三：用长方形还能框出几个数？怎样框？框出的数之间有什么关系？

学生试着用长方形框出4个数，有的横着框，有的竖着框。

在用长方形框数的活动中，教师让学生对框出3个数的方法及这3个数的关系进行探究，而对于框出4个数则是鼓励学生在已有活动经验的基础上进行。在每次框数的时候，教师都以明确的问题与要求让学生有针对性地“动手做”，这就使得学生真正经历了由挑战到思考再到挑战的过程。随着活动的深入以及教师的适时放手，学生的思维层层深入，他们不仅解决了数学问题，而且真正学会了数学思考。

四、彰显“思”的深度

在数学教学过程中，教师经常会采取回顾反思的形式来考查学生对所学知识的掌握情况。在“动手做”的教学中，教师及时引领学生对“做”的过程进行反思，以培养学生的反思意识，促进学生的数学思维走向深处。

以苏教版教材四年级上册“观察物体”单元编排的“动手做”为例（如图4）。

图4

这次“动手做”的内容包括两个方面：一是先让学生用5个大小一样的正方体摆成教材中要求的样子；二是让学生数一数图上正方体的个数，再摆一摆。基于此，教师可设计如下活动。

活动一：

1.想一想怎么摆。

2.分别从正面、右面、上面看看自己摆的图形是否与教材上的一样。如果不一样，则意味着摆放不符合要求，要重新摆。

3.与同桌交流，说说自己是怎样摆的。

活动二：

1.按照要求数一数正方体的个数。

2.按照每个图形的样子先摆好，再添加正方体，直至摆出长方体为止。一边摆一边数，并结合图形想象哪些正方体从正面看是看不到的，思考这些看不到的正方体的个数是多少。

3.学生交流摆放经验。

摆只有一层正方体的不规则图形很简单，缺哪补哪就行。摆有两层正方体的不规则图形可以采取分层补充的方法，先补下面一层，再补上面一层就行，就这样一边摆一边想，最后把添加的正方体的个数算一算就行了。

学生在摆正方体时，先是自己摆，然后对照教材中的图形，如果摆得不符合要求则重新摆。这个摆放自查、重新摆放的过程也是学生深入思考的过程，它使学生的反思能力与“动手做”的能力得到了提升。

五、立足“思”的发展

在数学教学中，教师应在关注“思”的路径、层次、深度等基础上，关注学生思维的发展，促进学生理性数学学习、构建数学知识体系，让整个学习活动顺利地走向更深处。其间，教师切不可忽略学生“动手做”的过程。

例如，在教学苏教版教材五年级下册的“分数的意义和性质”时，教师要善于捕捉教材中一些较为特殊的习题或内容，如图5的思考题。

图5

1.尝试探究，自主思考

首先，引导学生解读问题，引发学生的疑问。有学生提出：“这个问题没法解答，无论是计算三角形的面积，还是计算梯形的面积，高都是必须要知道的，题目没有给出高的长度，还怎么解呢？”

其次，引导学生深入分析疑问，让学生努力寻找解决问题的突破口。教师对学生进行点拨：“这个问题既然出现在教材中，就说明是编者做过很多思考才编排的，那是不是我们的研究方向不对呢？有没有新的思路？好好研究，老师相信你们一定能行的！”

教师的追问和激励性语言，让学生鼓足干劲，从不同角度思考问题，使学习活动顺利进行。

2.合作学习，共享思考

紧接着上述问题继续探究，教师还得搭建学习分享的平台，引导学生把自己的想法和研究成果展示出来，给其他人更多启发，从而实现学习的突破。

有学生提出：“可以假设这个梯形的高就是8cm，这回底和高都知道了，面积就能算出来了，对应的分率也很容易算出来。”也有学生提出：“假设梯形的高是8cm，那么小三角形和大三角形的高也是8cm，它们的高相同，是不是都可以用字母h来表示？这样也能算出结果。”还有学生提出：“因为三角形、梯形的高都相同，所以这些图形之间的面积比，实际就是底之间的比。”

总之，在数学教学中，首先要让学生学会“怎样思考”，因此，对于“动手做”来说，教师要把其本质定位为“数学思考”，从“做”入手，引领学生进行多层次“思”，让学生的数学学习真正走向深处，提升学生的数学实践能力。