例谈单元整体教学下的“你知道吗”整合路径

江苏苏州工业园区金鸡湖学校（215000）何晓燕

“你知道吗”是苏教版教材的一个特色栏目，也是教材的重要组成部分，它不仅介绍数学知识的历史演变，传递数学文化和数学思想，激发学生的爱国热情，关注学生数学兴趣的养成，还对学生的数学核心素养的形成有着举足轻重的作用。但因为这一部分内容并不在日常练习和考试范围中，所以没有引起教师的足够重视。日常教学中教师大多是将“你知道吗”作为课堂的点缀，要么是蜻蜓点水般地浅尝辄止，要么是采取完全忽视的态度，仅以一句“感兴趣的同学课后可以认真阅读”一带而过。

“你知道吗”这一部分内容在苏教版教材中主要涉及三个方面：关于数学的历史资料，教材中相关内容的适度拓展或补充，与其他学科和社会生活相关的整合性知识。因此，教师不能把这部分内容不加以解读就直接使用，而应将其当作一节课来机动安排。那么如何用好“你知道吗”？应该以怎样的方式将其融入单元整体教学中？现就“起”“承”“转”“合”这四种基本路径结合具体课例进行阐述。

一、“起”——细微之处见真章

有一类“你知道吗”是介绍与本单元知识相关的数学知识的发展历程，通过传递数学思想，介绍数学家及其探究精神，让学生了解数学知识和数学文化。教师选择“你知道吗”开启主题单元的整体探究时，可通过融合、整合，借助整体教学让隐性的数学文化显性化，让静态的知识动态化。以“你知道吗”为载体，创设情境任务开启新单元的学习，能让学生从单元内容、学习方法上“俯视”整个单元，形成对单元整体的认知，同时教师能够了解学生对新知学习的“最近发展区”。

【教学案例1】关于”天元术“的介绍（如图1）

图1

1.介绍“未知数”

启发：在图1中，哪些是已知数？哪些是未知数？怎样表示它们？

明确：我们可以用字母x表示这个未知数。

介绍：“天元术”。

2.介绍“方程”

引导：50+50=100、x+50=150、2x=200三个等式如何分类？

启发：在等式中让未知数与已知数一样平等地参与运算，在表达形式上让未知数和已知数之间建立一种表示相等的关系。

小结：方程的定义。

介绍：数学史料——笛卡儿与用字母表示数。

其实，提及方程，就不得不联想起刘徽在《九章算术》中提出的“以御错糅正负”。这一精辟论断明确指出了方程的价值。“错糅”，在认识并去理解和表达复杂的现实时，首先想到的就应该是提取数量关系，这样才能用最简洁的内容去表达等量关系；列方程背后所具有的建模思想，彰显了数学思想方法的永恒魅力。如何让“你知道吗”中承载的内容凸显文化的魅力？显然，这需要整合重组、有机融合、相机嵌入。利用“你知道吗”就能开启单元整体学习的篇章，见微知著，适时放大，从而引领学生进入新的探究领域。

二、“承”——上下求索而求通

从单元整体知识中的某一知识点发散开来，寻找、搜集、联结相关的数学史、数学文化资料，就能获得对数学知识以外的思想方法以及文化底蕴的认知和思考。有一类“你知道吗”恰恰就是对单元整体的补充、拓展和延伸，对其重新加工后创设问题情境，能引领学生深度思考，让学生在动手操作、实践探究等活动中获得知识，感悟数学思想方法，提高数学素养。

【教学案例2】关于二进制的介绍

图2

在用十进制表示多位数后，教材引入了“二进制及二进制的运用”的介绍。二进制的抽象表述是难以让学生读懂和理解的。学生从启蒙之初便开始接触十进制计数法，对十进制这一计数体系和规则非常熟悉，甚至有根深蒂固的认识，而二进制则打破了现有的认知平衡。因此，结合“你知道吗”中介绍二进制是用0和1两个数字表示的数，教师可以提出核心问题：“在每一数位只有一个算珠的计数器上能不能拨出2？如果能，怎么拨呢？”这个问题让学生原有的认知经验受到了巨大的冲击，学生强烈的好奇心和探究欲一下就被激起了。在静静的思考和热烈的讨论中，学生能够突破固有的思维定式：既然不能“满十进一”，那就“满二进一”吧。

二进制在表达时只需用到0、1两个数字，只有两个数字却可以组合出从1开始的任意一个自然数。这是十进制所不具备的特征，而这种完全陌生且充满了全新逻辑顺序的进制表达方式，学生理解起来是困难的。这时可将二进制渗透到以下的数学游戏中：

年龄范围从1岁到63岁，只要一个学生拿着六张卡片提问“这张卡片上有没有你的年龄？”，就能通过被猜者回答的“有”或“没有”猜出他的年龄。

图3

这六张卡片的第一个数字1、2、4、8、16、32分别是“2”转换成十进制后的数，即20=1，21=2，22=4，23=8，24=16，25=32。制作卡片时先把1～63各数转换成二进制的数来表示，再按类别记在相应的卡片上。这样，将“你知道吗”与数学游戏相结合，为学生进一步学习二进制奠定了坚实的基础。

三、“转”——横看成岭侧成峰

不关心知识的来龙去脉与相互联系，知识呈现的样态就是零散的，学生对于知识的学习可能也是“不识庐山真面目，只缘身在此山中”。而“转”就是基于“你知道吗”对单元整体的深度探索，通过追本溯源，引领学生在动手操作、实践探究等活动中发现知识，感悟数学思想方法，提高数学素养。

可以是基于“你知道吗”对教材中某一概念进行刨根问底的探究，也可以是对某一重难点知识的深入挖掘、开发，还可以是对某一数学思想方法的渗透、提炼。

五年级上册教材在“多边形的面积公式推导”之后，编排了“你知道吗”（如图4）来介绍刘徽的割圆术——以盈补虚。通过对数学史实的简要介绍，激发学生探究“割圆术”，同时将这一方法和之前的面积公式的思维方法相联系，促使学生发现解决问题的根本方法：将未知图形转化成已知图形，将新知识转化成旧知识。

图4

【教学案例3】探究“割圆术”

师：通过了解，我们不禁为我国古代数学家的智慧感到骄傲和自豪，也有同学十分好奇——能用“割圆术”将梯形转化成学过的其他图形吗？请拿出探究单，想一想，可以将梯形割补成其他什么图形？

生1：我刚才试过了，可以从梯形的两条腰的中点向下到底边画两条垂直的线段，沿着这两条垂直线段剪下两个小三角形，拼接到上面，就能把梯形转化成长方形。（如图5）

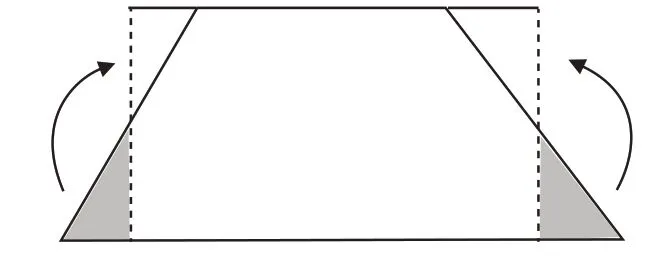
图5

生2：我跟他的想法不一样。我是先连接一条腰的中点和上底的一个顶点，得到一条线段，沿线剪下三角形后，再通过旋转和平移，把梯形转化成一个大三角形。（如图6）

图6

师：原来梯形不仅可以像最初学习之时将两个完成一样的梯形拼成一个平行四边形，还可以转化成长方形、三角形，只要转化成学过的图形，那么面积计算就不是问题啦！

在操作、交流、讨论、思考、质疑等活动中，学生不仅能够体会不同的割补方法，明确解决问题的方法多种多样，还能深刻且全面地理解教材中“你知道吗”的知识，丰富对面积计算转化思路的认识。

转换视角，从不同角度来解读教材，对“你知道吗”多元化的解读颇有“横看成岭侧成峰”的意韵。

四、“合”——为有源头活水来

苏教版教材“两位数乘两位数”单元中的“你知道吗”，介绍了我国古代“铺地锦”的乘法计算方法。这一内容可以与探索新知融合，以引导学生经历数学方法“再创造”的过程，使学生能够领略数学家的智慧，感悟数学思想方法。

在教学中，把“铺地锦”的乘法计算方法和教材中的竖式计算方法的学习融合在一起，能从单元整体教学的角度使得学生经历完整的探索过程。在学生学习两位数乘两位数的竖式计算后，教师先出示第一幅图（即62×37），引导学生思考：“这个算式是什么意思？”学生通过观察和推理，了解了方格的上面和右面表示两个乘数，而方格里的数分别表示3和6以及3和2相乘的积。此刻是将现代竖式计算的格式和古代“铺地锦”计算相结合进行“再创造”的最佳时机。教师追问：“这两种计算方法有没有相同之处？”学生很快发现，其实算理是一样的：都是用第二个乘数十位上的3分别去乘第一个乘数。之后，教师鼓励学生尝试进行第二步的“铺地锦”计算，同时想想每步算的是什么。这样，学生不仅知道了“铺地锦”计算，而且深刻感受了古今计算方法的融会贯通。可见，顺势探究，能将相关知识串成一条线，“合”起来拧成一股绳，发挥巨大的作用，为学生的数学学习输送源源不断的“活水”。

对“你知道吗”的知识的挖掘和补充，能起到“起—承—转—合”的作用，从而促进学生深刻地理解数学知识，感悟数学思想方法的魅力，同时还能激发学生探究的欲望，培养学生的数学核心素养。