振动慢剪破碎机内锥动力学分析

蔡改贫，郝书灏，黄金若，胡 振

(江西理工大学 a. 机电工程学院；b. 江西省矿冶机电工程技术研究中心，江西 赣州 341000)

近年来，随着科学技术的不断发展，能源的消耗持续增加，国内外研究人员对充分利用能源和节能降耗的课题进行了深入的研究[1-3]。在矿业生产活动中，矿产资源主要是通过破碎以及研磨之后才能得到充分的利用，所以研究矿产资源的破碎是实现能源充分利用和节能降耗的根本任务之一[4-8]。振动慢剪破碎机作为一种矿石破碎设备具有非常重要的研究意义以及研究价值，如何在提高破碎机工作效率的同时降低能耗是当前重要的研究课题[9-10]。

由于振动慢剪破碎机的破碎力主要是外锥在做绕整机中心轴线的旋转运动以及内锥在做振动时产生的冲击运动所提供的，外锥的圆周运动较为简单，内锥的振动运行形式较为复杂，所以本文中主要针对振动慢剪破碎机内锥的动力学进行研究，主要是对内锥的动力学模型进行建模分析，对内锥的动力学响应进行分析，利用机械系统动力学自动分析软件(automatic dynamic analysis of mechanical systems, ADAMS)进行空载下的动力学响应仿真分析和利用工程离散元分析(EDEM)与ADAMS耦合进行负载下的动力学响应仿真分析。

1 振动慢剪破碎机工作原理

振动慢剪破碎机是本课题组研发的一种新型细碎的矿石破碎设备，其结构简图如图1所示。振动慢剪破碎机外锥在外锥齿轮的带动下做绕整机中心轴线的旋转运动，内锥在立式激振器的带动下做振动运动，利用外锥以及内锥运动所提供的破碎力，对矿石进行剪切、挤压、冲击、劈裂，从而实现矿石的细碎。该振动慢剪破碎机具有细碎效果好、破碎产品粒度均匀、处理量大等优点，可以高效完成细碎矿石作业[11]。

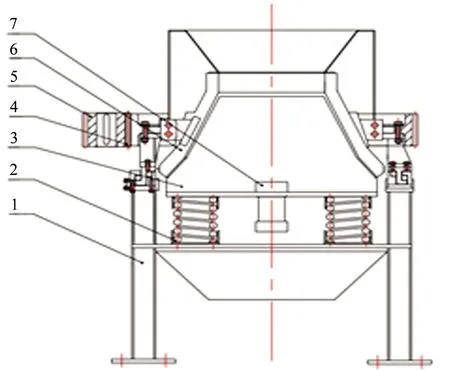
1—机架；2—主振弹簧；3—破碎机内锥；4—破碎机外锥齿轮；5—传动齿轮；6—破碎机外锥；7—立式激振器。

2 振动慢剪破碎机内锥动力学模型

振动慢剪破碎机内锥的振动运动是一种非线性多自由度的振动系统，其运动形式十分复杂。内锥做空间自由运动，即在X、Y、Z方向的平动以及绕X、Y、Z方向的转动，共有6个自由度r。通过分析，振动慢剪破碎机内锥简化力学模型如图2所示，其中，m0是偏心块质量，m1是内锥质量，k是主振弹簧刚度，x、y、z为3个方向上的位移，α、β、γ为X、Y、Z方向上的转动角度。

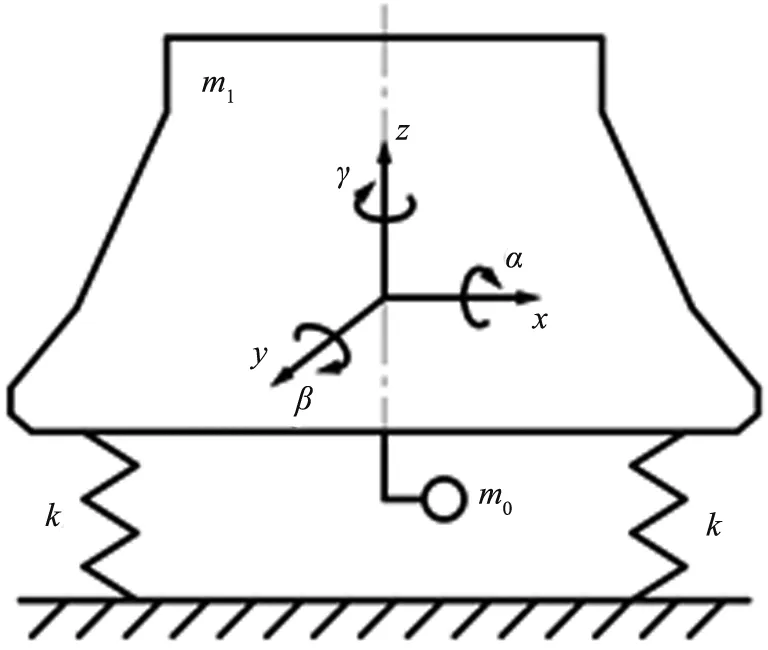
图2 振动慢剪破碎机内锥简化力学模型

利用拉格朗日方程建立振动慢剪破碎机内锥动力学方程[12-13]，该系统的振动方程可由动能、势能等来表示，即

(1)

式中：Qr为对第r个广义坐标的广义力，N；t为时间，s；E为系统的动能，J；qr为第r个自由度的广义坐标；U为系统的势能，J。

2.1 系统的动能

系统的动能由偏心块的动能以及内锥动能组成，其表达式为

(2)

其中

ωx=α′cosβcosγ+β′ sinγ,

(3)

ωy=-α′ cosβsinγ+β′ cosγ,

(4)

ωz=α′ sinβ+γ′,

(5)

式中：Em0为偏心块的动能，J；Em1为内锥的动能，J；i为0,1;x0、y0、z0为偏心块在X、Y、Z方向的位移，m；x1、y1、z1为内锥在X、Y、Z方向的位移，m；j为0，1；Ix0、Iy0、Iz0为偏心块在X、Y、Z方向的转动惯量, kg·m2；Ix1，Iy1，Iy1为内锥在X、Y、Z方向的转动惯量，kg·m2;j为0，1；ωx、ωy、ωz为内锥和偏心块在X、Y、Z方向的角速度，rad/s；α、β、γ为X、Y、Z方向上的转动角度, rad/s。

由于偏心块的动能计算十分复杂，因此本文中采用坐标变换求解其位置，然后进行求导得到其速度，再计算偏心块动能。偏心块安装在内锥上，其运动后的绝对坐标为

(6)

式中：e为偏心块的偏心距, m；ω为偏心块的角速度, rad/s。

2.2 系统的势能

系统的势能由弹簧的变形势能组成，其计算表达式为

(7)

其中

(8)

(9)

(10)

式中：Uk为弹簧的势能，J；kx、ky、kz为弹簧在X、Y、Z方向的刚度，N/m；xk1、yk1、zk1为在X、Y、Z方向的变形后的坐标, m；xk、yk、zk为在X、Y、Z方向的变形前的坐标, m。

系统的总势能表达式为

(11)

2.3 振动微分方程

系统的广义干扰力为系统中的非理想约束的反力，即阻尼。将前文求得的系统动能、势能以及广义干扰力代入拉格朗日方程式(1)中，可以建立振动慢剪破碎机内锥6个自由度振动微分非线性方程组，通过进行相应的简化以及线性化处理[14-15]，得到内锥六自由度振动微分方程组：

(12)

2.4 振动慢剪破碎机内锥动力学响应

结合自制的实验样机，可以得到振动慢剪破碎机系统参数，如表1。根据所建立的破碎机空载状态下内锥的六自由度振动微分方程组，利用MATLAB(矩阵实验室)数学分析软件求解可以得到系统在平面上的动力学响应，内锥质心的平面运动计算轨迹如图3。结合图分析可知，内锥在X、Y方向上的位移范围为-0.6～0.6 mm，整体振幅为1.2 mm，振动慢剪内锥的运动主要为水平面上的振动圆运动，其运动轨迹整体呈现一定的规律性，是一种非线性概周期运动。

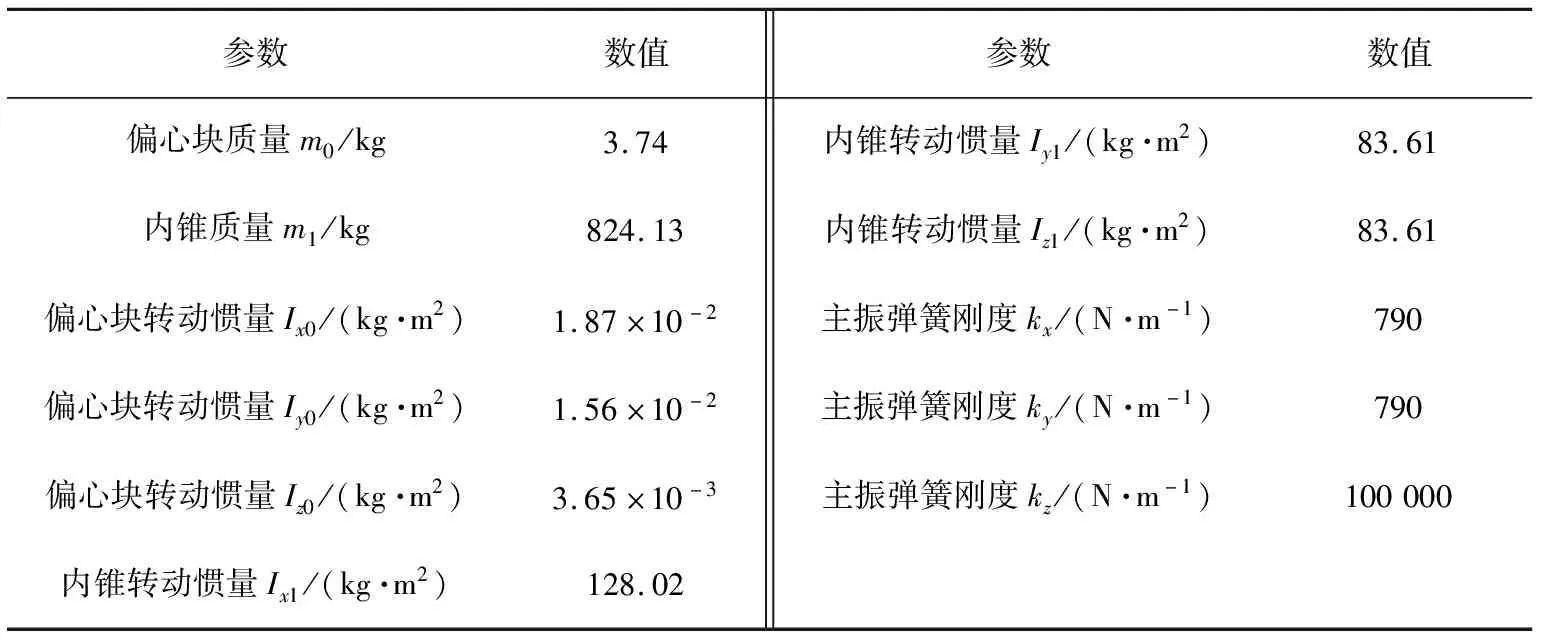
表1 振动慢剪破碎机系统参数

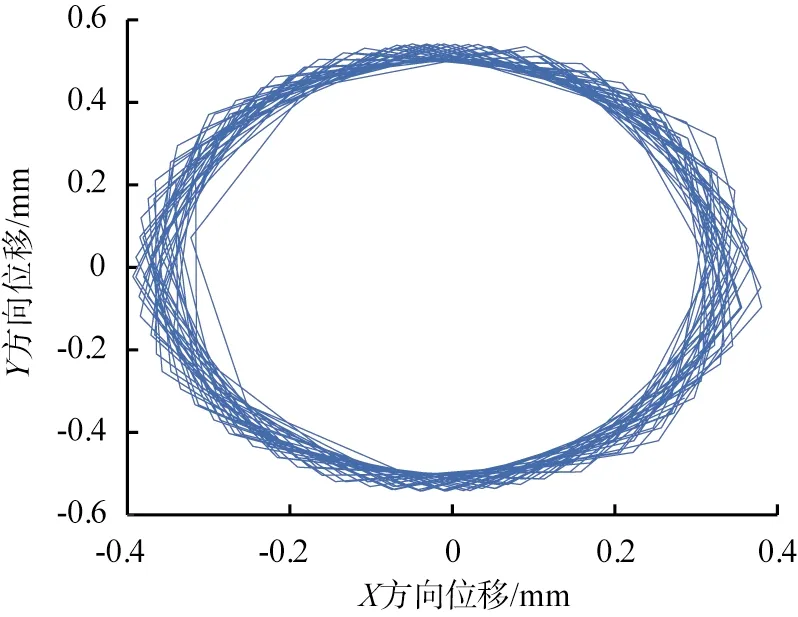
图3 内锥质心的平面运动计算轨迹

3 内锥运动仿真分析

3.1 内锥虚拟样机模型的建立

在UG中建立振动慢剪破碎机内锥、内锥底盘、振动电机主体、偏心块等三维几何模型，同时按照实际位置进行装配，内锥虚拟样机三维几何模型如图4所示。在UG中将装配体以Parasolid格式将模型导入到运动学分析软件ADAMS中，按照样机实际情况添加各部件的材料属性；根据振动慢剪破碎机实际约束情况，添加连接关系，其中内锥与内锥底盘之间为固定连接，内锥底盘与振动电机主体之间为固定连接，振动电机主体与偏心块之间为旋转连接；在振动电机主体与偏心块之间施加电动机驱动，其驱动函数为STEP(time, 0, 0, 6, 1 450×2×PI)+STEP(time, 16, 0, 18,-1 450×2×PI)，代表在0～6 s时偏心块转速由0增加为1 450 r/min，在6～16 s时偏心块稳定运行转速为1 450 r/min，在16～18 s时偏心块转速由1 450 r/min降低为0；添加内锥底盘与机架(大地)之间的弹簧模型，传统弹簧模型仅有轴向运动，不能满足实际需要，所以为满足内锥底盘与机架之间的弹簧实际要求，本文中采用ADAMS中的Bushing，其可以提供6个方向上的刚度与阻尼。建立的振动慢剪破碎机内锥虚拟样机装配模型，如图5所示。

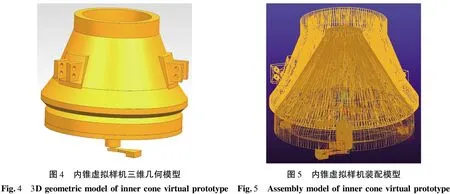
图4 内锥虚拟样机三维几何模型Fig.4 3Dgeometricmodelofinnerconevirtualprototype图5 内锥虚拟样机装配模型Fig.5 Assemblymodelofinnerconevirtualprototype

3.2 内锥运动状态仿真及结果分析

在虚拟样机模型中，在内锥质心位置上标记一个MARKER点，以该点的运动轨迹来描述内锥运动状态。仿真完成后，在后处理中可以查看仿真结果，将仿真数据导出，经过MATLAB软件分析可以得到该MARKER点的平面的位移图像，内锥质心的平面运动轨迹如图6所示。

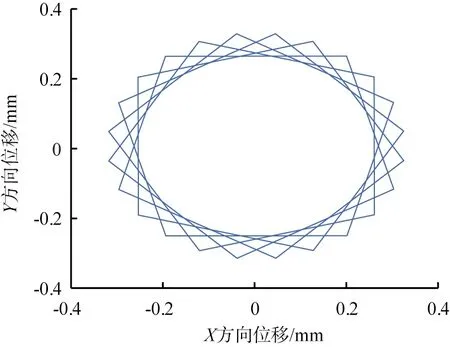
图6 空载时内锥质心的平面运动轨迹

分析图6可知，其仿真结果与建立的振动慢剪破碎机动力学模型所求的动力学响应结果一致，其内锥的主要运动为水平面上的振动圆运动，内锥在X、Y方向上的位移范围为-0.4～0.4 mm，整体振幅为0.8 mm。

4 破碎仿真试验

4.1 基于EDEM与ADAMS的破碎仿真模型

为探究振动慢剪破碎机在负载情况下的内锥运动情况，将EDEM与ADAMS进行耦合仿真[16]。将UG中建立的振动慢剪破碎机三维模型分别导入到EDEM与ADAMS，利用ADAMS Co-simulation实现2款软件的耦合仿真，其中EDEM提供颗粒信息，ADAMS提供运动信息。

ADAMS中主要的设置过程已在3.1节进行介绍，EDEM中按照实际情况选择入料粒径为35～45 mm，破碎模型选择Tavares破碎模型[17-18]，表2为钨矿石颗粒与内、外锥的材料参数。

表2 材料参数

4.2 破碎仿真结果的分析

在EDEM后处理中的破碎仿真效果如图7所示，由图可知，矿石颗粒呈分层破碎，上部颗粒粒径较大，进入排料口区域的矿石颗粒较小，其中入料粒径为30～45 mm、排料粒径为0.36～18 mm，与实际破碎过程相符。

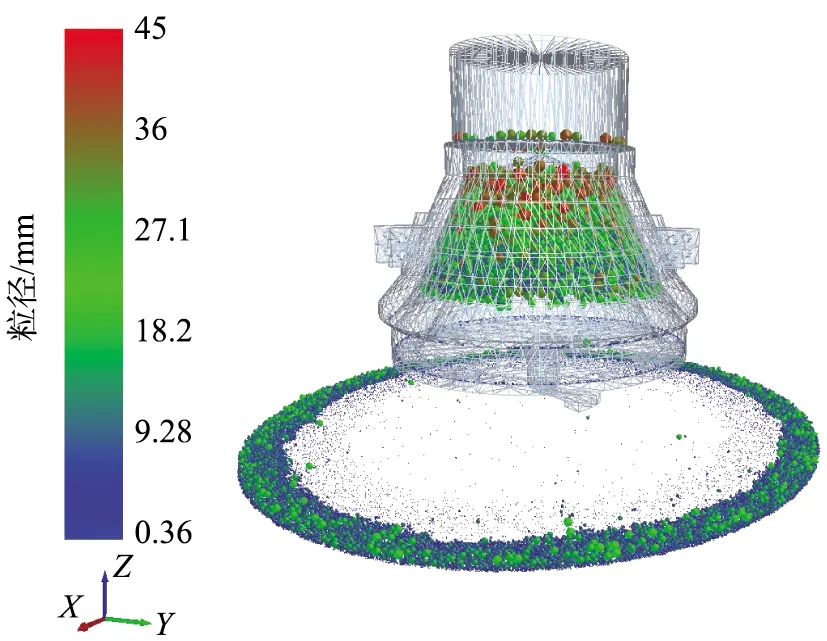
图7 EDEM中破碎仿真效果

为探究振动慢剪破碎机在负载情况下的内锥运动情况，将破碎模拟结果通过ADAMS导出内锥质心MARKER点的X、Y方向位移数据，通过MATLAB数学处理软件，绘制内锥负载情况下在平面内的运动轨迹，如图8所示。分析图8可知，其内锥的主要运动为水平面上的振动圆运动，同时在负载的作用下，内锥在X、Y方向上的位移范围为-0.3～0.3 mm，整体振幅为0.6 mm，与空载情况下的X、Y方向上的位移范围为-0.4～0.4 mm，整体振幅为0.8 mm相比，振幅减小。

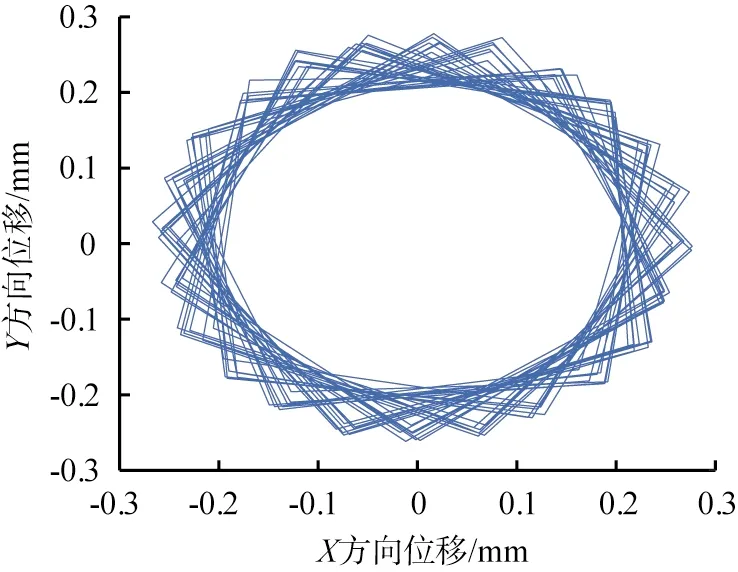
图8 负载时内锥质心的平面运动轨迹

5 结论

1)通过建立振动慢剪破碎机内锥的动力学模型，使用MATLAB软件，得到内锥的动力学响应，其主要运动为水平面内的振动圆运动。

2)使用ADAMS建立内锥的虚拟样机模型，采用内锥标记MARKER点的方式描述内锥的运动轨迹，获得空载下的内锥运动轨迹。使用ADAMS与EDEM耦合的方式，采用Tavares破碎模型，仿真振动慢剪破碎机钨矿石颗粒破碎过程，分析内锥在负载下的运动轨迹，与所建立的空载下虚拟样机模型内锥仿真运行轨迹、计算轨迹基本吻合。

3)通过数值计算、仿真、耦合仿真方法，验证了振动慢剪破碎机结构设计的合理性，证明了破碎机部件的设计参数具有可行性，可为后续设计提供参照依据。