离心双涡流快速热解器的场流机制及协同强化传热

赵泽华，杨景轩，张 楠，韩碧龙，牛昊锐，郝晓刚

(太原理工大学 化学工程与技术学院，太原 030024)

我国实现“双碳”目标离不开对煤炭、石油等传统化石能源利用方式的变革。变革方向之一是将煤炭视为碳资源，通过清洁高效利用技术，生产基础化学品、高端材料等。另一方面，生态建设作为固碳的重要手段将获得进一步发展，由此产生的数量可观的农林废弃物等生物质资源值得进一步挖掘，以补充传统化石能源退出形成的空白。这两个方面都离不开化工工艺流程的再造，也为新装备的开发提供了契机。

以热解、气化为代表的热化学转化技术是目前较为成熟的煤/生物质清洁高效利用技术。通过不同热化学转化技术的组合，如三塔式循环流化床工艺[1]，可以实现碳资源的分质梯级利用，提高工艺系统的总体能效[2]。快速温和的热解技术可以高效提取出煤/生物质中蕴含的芳香结构和环烃等高值大分子[3]，适合作为梯级利用工艺的先导。在热解反应器方面，颗粒顺重力场流动的下行床具有停留时间短、固体返混少、接近平推流型的特点，而这些特点恰好契合反应迅速、且目标产物为中间产物的煤/生物质热解工艺的需求[4]。但下行床床层固含率较低[5]，传热速率不高[6]，限制了其在以颗粒为热源的内热式工艺中的应用。针对下行床固含率低的问题，文献报道了三种改进思路：降低操作气速[7]，改变下行床结构[8]，提升系统颗粒循环通量[9-11]。前两条技术路径下，床层固含率大都处于10-2数量级，提升有限；第三条技术路径可以将局部固含率提升到0.165[11]，但需要引入额外的单元设备，其他单元设备也因配合需要增加了自身负荷，系统复杂度的增加会产生更多的工程问题。因此，有必要在下行床中引入新机制以进一步提升固含率。

针对以上问题，郝晓刚等[12]提出了离心双涡流快速热解器的技术构想，在下行床中引入离心力场，通过颗粒在器壁的浓集获得局部高固含率以增强传热速率。ZHANG et al[13]采用CFD-DEM方法对该技术构想进行了初步研究，结果表明，在较高颗粒通量下，离心力场机制可以将局部固含率提升至0.25左右，且从入口到出口保持稳定，明显改善了下行床中固含率不足的问题。同时，旋风反应器保留了下行床中停留时间短、固体返混少、接近平推流型的特点。

前期对离心双涡流快速热解器的研究聚焦于离心力“场”机制对固含率的提升作用，本文进一步阐述其中的“流”机制，剖析“场”“流”机制的互动及其对强化传热的协同效应。

1 离心双涡流快速热解器中的“场”和“流”

离心双涡流快速热解器可嵌入煤/生物质资源化梯级利用系统(图1)，利用系统中循环的载热颗粒加热煤/生物质颗粒。设置两个矩形入口分别对接两种颗粒。入口与筒体相切，切流造旋机制产生离心力场。气固两相进入后顺重力场下行，颗粒从底部流出。气流首先旋转下行，形成外层旋涡，期间不断有部分气流折返，并在某一位置全部气流完成折返，折返气流旋转上行，形成内旋涡，从顶部出口流出。本文中，“场”特指颗粒旋转产生的离心力场，“流”特指内外双层气旋涡流。

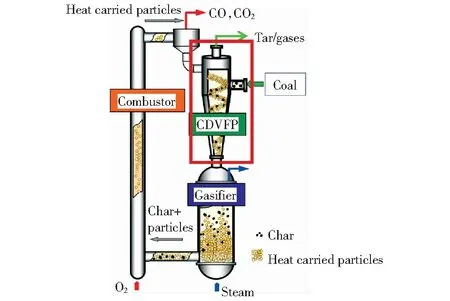
图1 热解-气化-燃烧耦合煤/生物质资源化梯级利用系统Fig.1 Pyrolysis-gasification-combustion coupling coal/biomass resource cascade utilization system

2 研究方法

2.1 CFD-DEM模型

综合考虑模拟计算效率与精度要求，选择离散单元法(CFD-DEM)进行模拟。该方法是基于欧拉-拉格朗日参考系的方法建立的，适用于探究流场与颗粒场之间的相互作用。气相作为连续相，其运动是求解模拟单元内纳维斯托克斯方程，采用雷诺应力方程考虑流体在反应器内的湍流行为。颗粒相被模拟做离散相，单个颗粒采用牛顿第二定律计算。本文采用Gidaspow曳力模型计算气固之间曳力。模型所选用的主要参数列于表1和表2.

只考虑反应器中颗粒间的热传导、热辐射和气体的对流传热，颗粒与反应器壁面无热量传递。其中对流传热模型为：

Qcond=hpfApΔTpf.

(1)

式中：p代表颗粒，f代表流体相，A为传热面积，ΔT为温差，hpf为传热系数，定义如下：

(2)

式中：λq是流体的导热系数；dp是颗粒的直径；Nup为努塞尔特准数。

颗粒热传导模型为：

Qconv=hcΔTp1p2.

(3)

(4)

式中：kp为颗粒的热传导系数，FN是法向接触力，r*是Heartz完全弹性接触理论的几何半径，hc是不同颗粒间的传热系数，E*是双颗粒的有效杨氏模量，方程右边括号内的算式表示颗粒间的接触面积。

热辐射模型：

(5)

式中：εp为球形辐射率，σ是斯蒂芬-波尔茨曼常数，A是颗粒的表面积，Tp是颗粒温度，Tlocal是封闭网格内颗粒的平均温度。

离心双涡流快速热解器直径是52 mm，筒体和锥体高度分别为120 mm和360 mm，矩形入口高宽分别为30 mm和13 mm，中心排气管直径26 mm，长21mm，排料口直径21 mm。采用非结构化网格离散。综合考虑计算时间和计算结果的可靠性，经网格无关性考察，最终选用120 000网格进行计算。采用传统下行床反应器作为对照，其主体为直径52 mm的圆柱，高2.6 m，顶部仅有载热颗粒进入，顶部以下0.1 m处安装有径向双管喷嘴，喷嘴直径25 mm，煤颗粒以0.5 m/s速度进入。其他参数列于表1和表2.

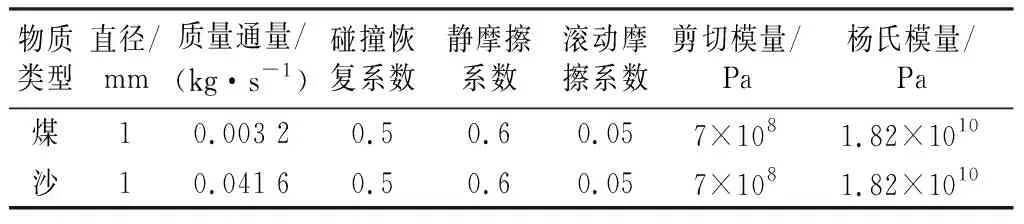
表1 颗粒特性参数Table 1 Characteristic parameters of particles

表2 颗粒与气体特性参数Table 2 Characteristic parameters of Particle and gas

2.2 验证

采用上述模拟方法分析颗粒在旋风反应器中的停留时间，与实验测试结果对照验证模拟方法的可靠性。KANG et al[14]报道了煤半焦颗粒(密度为1 700 kg/m3，粒径为178 μm)在一种与CDVFP构型相近的旋风反应器中的停留时间分布。实验与模拟结果如图2所示。平均停留时间的模拟值为1.53 s，实验测量值为1.46 s，二者相差4.8%.采用公式(6)计算停留时间跨度tsp：

(t90-t10)/t50=tsp.

(6)

式中：t10表示停留最短的10%颗粒的停留时间上限值，以相同的方式定义t50和t90.实测停留时间跨度是0.458，模拟计算值为0.490，二者相差约7%.

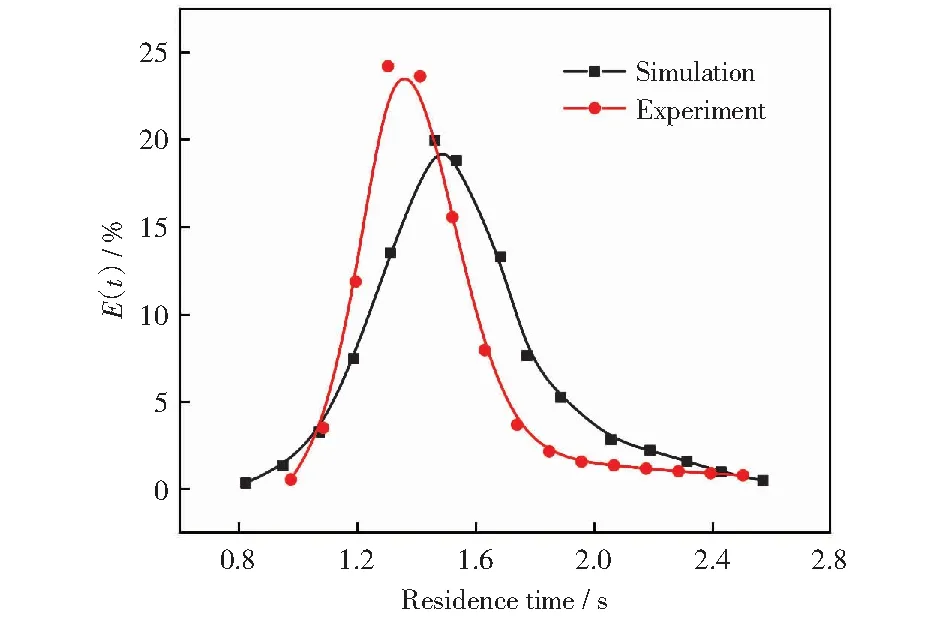
图2 停留时间分布Fig.2 Residence time distribution

误差在工程可接受的范围之内。本文所用CFD-DEM耦合方法可以较准确地预测颗粒在反应器中的运动。

3 结果和讨论

3.1 双涡流特征

离心双涡流快速热解器中内外双层旋涡的典型结构是准兰金涡。气流切向速度图如图3(a)所示，外旋流呈准自由涡，内旋流呈准强制涡。切向速度在二者交界处达到最大，约是入口气速的1.2倍。当高通量颗粒进入后，由于气固间存在速度差，气流向颗粒流传递动量，自身旋转速度急剧衰减，最大切向速度衰减了约85%.离心力场由颗粒旋转产生，“场”通过颗粒削弱了“流”。

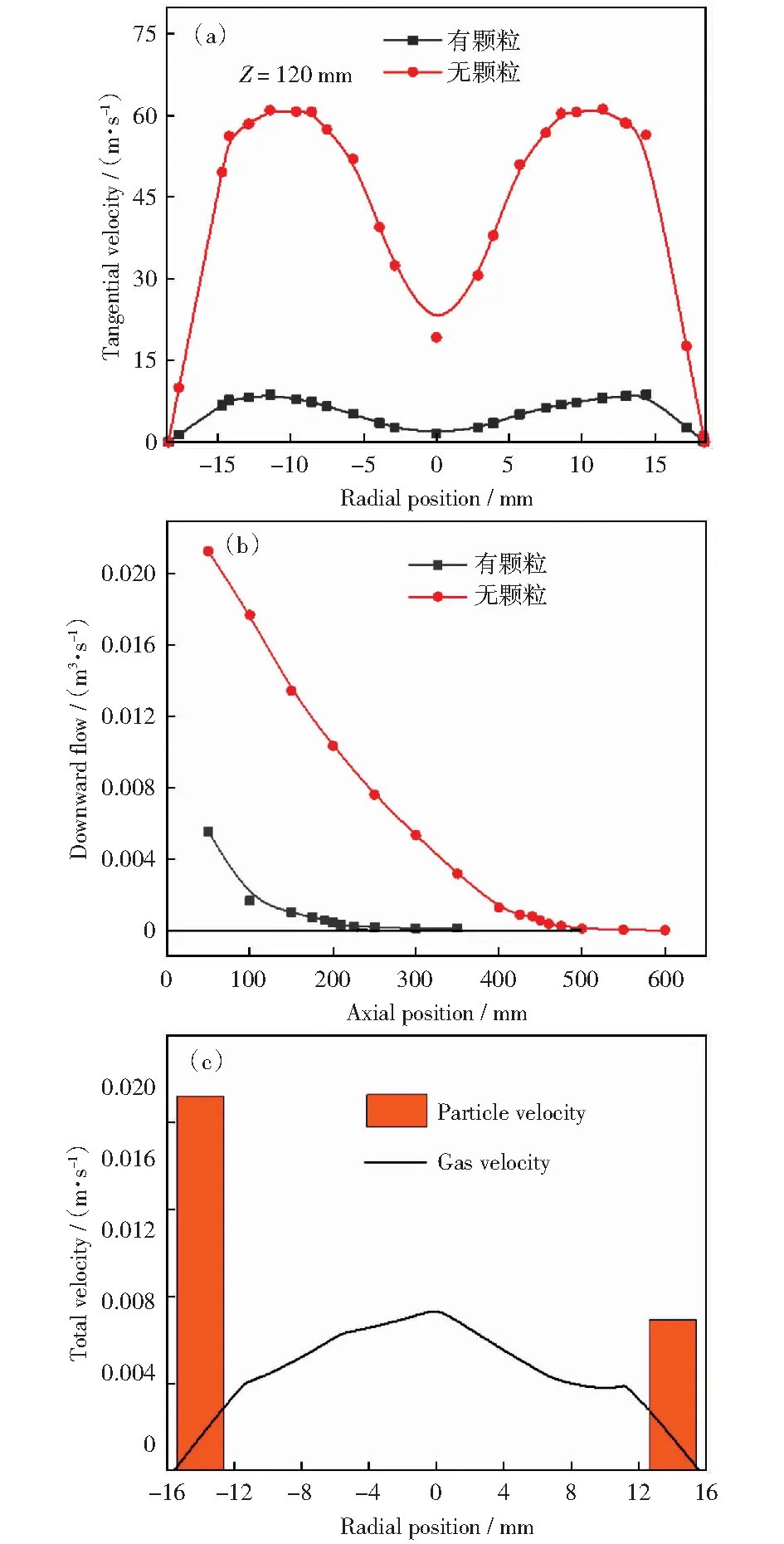
图3 CDVFP中气流速度特征Fig.3 Velocity characteristics of airflow in CDVFP

图3(b)展示了热解器内不同轴向位置处下行气体流量。下行气流量接近零的位置可认为是气流折返点，气流折返点与排气管之间的距离定为气旋长度。纯气流在热解器内经历了约500 mm的下行距离才完全折返；加入颗粒后，气体向颗粒传递动量，自身能量迅速衰减，所能支撑的气旋长度缩短了50%，明显小于热解器高度。由此，气旋尾端将热解器区分为气固互作用规律完全不同的两段：气旋尾端以上，气流运动受控于热解器结构，呈现准兰金涡结构，向颗粒传递动量；气旋尾端以下，准兰金涡结构近乎消失，气速低于颗粒速度(图3(c))，动量传递方向逆转，由颗粒指向气流。

3.2 颗粒分布及速度特征

离心双涡流快速热解器内颗粒分布如图4所示。为定量描述颗粒的分布特性，将热解器圆形横截面分为8个区域，统计每个区域内边壁附近的颗粒数量和平均速度。在空间分布方面，颗粒在器壁形成稀密相两种结构：部分颗粒堆叠团聚形成密相，部分颗粒分散紧贴器壁形成稀相。无载气或载气流速较低时，密相呈现螺旋带状，纵贯热解器上下；载气速度提高，螺旋颗粒带被打破，虽有局部浓集，但总体趋势是沿周向分布更加均匀。虽然颗粒聚集在器壁附近是离心力场直接作用的结果，但“流”对具体的分布状态有显著影响。

将颗粒速度分解为切向旋转速度和轴向下行速度两个分量，如图5所示。入口气速增加，颗粒旋转速度增加，下行速度却减小。颗粒加速旋转增强了离心力场，离心力场的增强加剧了颗粒与器壁间的摩擦，进一步抵消了重力的加速作用，颗粒的下行速度随之减弱。“场”“流”协同将颗粒下行速度保持在较低的范围内，这进一步提升了床层固含率。

在离心双涡流快速热解器中颗粒聚集在边壁，而传统下行床中颗粒分布均匀。因此，本文以包含所有近壁颗粒的圆环空间(径向尺度约3 mm)为基准统计固含率，结果如图6(a)所示。随着颗粒的下行，固含率不断提升，在排尘口处达到最大，原因在于横截面积不断收缩。入口气速增加，颗粒下行速度减小，同样高度的轴向空间容纳了更多颗粒，固含率随之增加。因此，离心双涡流快速热解器中固含率的提升是“场”“流”协同作用的结果：“场”将颗粒聚集在器壁，“流”减缓颗粒下行速度。

采用CHENG et al[15]建议的方法计算混合指数评估离心双涡流快速热解器中“场”“流”机制对二元颗粒混合的影响，结果如图6(b)所示。在颗粒下行过程中混合指数逐步增加，混合趋于均匀，这与常规下行床相同。CHENG et al[15]研究了切流进料下行床中煤与石英砂颗粒的混合指数，其颗粒通量(87.5 kg·m-2·s-1)和气速(10 m/s)与本文相近。在同样的无量纲位置处，常规下行床中二元颗粒的混合指数远高于离心双涡流快速热解器中的结果。“场”机制对二元颗粒混合有阻碍作用。相反，“流”则起促进作用。在高气速下，二元颗粒的混合均匀性很快达到了最大，并且在下行过程中基本保持不变。

图4 颗粒的空间分布及速度特征Fig.4 Distribution and velocity of particles in the CDVFP

图5 切向和轴向速度分量Fig.5 Tangential and axial velocity in CDVFP

3.3 传热特征

图7展示了颗粒在下行过程中的温度变化。颗粒在3个反应器中的停留时间都是(0.60±0.03) s，颗粒初始温度相同，传热终温的差异缘于传热速率的差异。在“场”“流”机制的协同作用下，离心双涡流快速热解器内煤颗粒的温升速率(>450 K/s)相比下行床有明显提高，达到了快速热解的要求(>100 K/s).在传统下行床中，尽管煤颗粒终温较低，载热颗粒的温降却更剧烈，更多的热量被气流接收；而离心双涡流快速热解器内则正相反，“场”“流”机制减少了传热过程中的损失，提高了传热效率。传热效率提高的另一个优势在于显著缩短了反应器高度。离心双涡流快速热解器高度仅是下行床的1/4.不仅节约了设备投资，也为循环流化床系统的优化提供了空间。

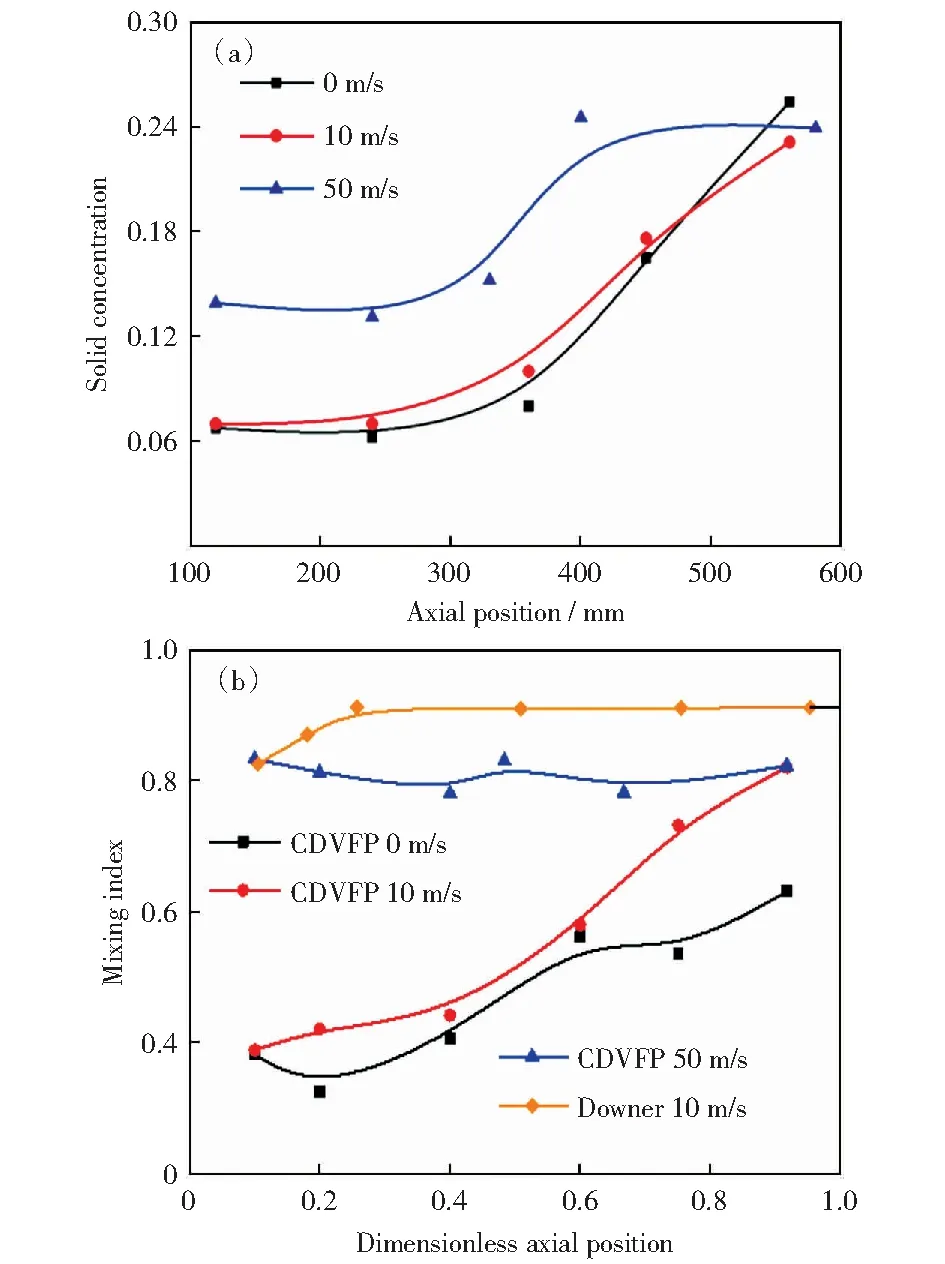
图6 二元颗粒固含率和混合特征Fig.6 Solid holdup and mixing index of binary particles in CDVFP

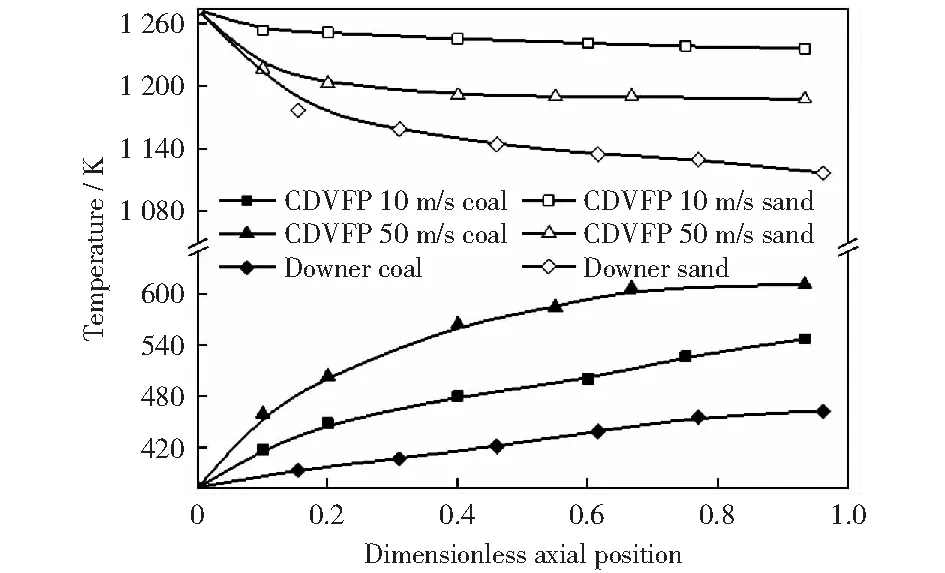
图7 二元颗粒温度分布Fig.7 Temperature distribution of binary particles

4 结束语

离心双涡流快速热解器内离心力场和内外双层气流旋涡相互作用。颗粒经切流造旋作用产生的离心力场会削弱气体旋涡的强度和长度。在气旋长度内，气流向颗粒传递动量，在气旋长度之外，动量传递方向逆转。气流向颗粒传递动量促进了颗粒沿器壁周向分散，增强颗粒的旋转速度。颗粒旋转速度的增加提高了离心力，从而增强了颗粒与器壁间的摩擦力，降低了颗粒的下行速度。这一效应与颗粒离心聚集效应协同，提升了床层固含率。离心双涡流快速热解器中二元颗粒的混合均匀性虽逊于下行床，但传热速率有明显增强，同时传递过程中的热损耗也减小。“场”“流”协同强化了二元颗粒间的传热。