多孔介质孔隙结构模型及其在渗流分析中的应用

胡黎明，林丹彤，张鹏伟，2，张兴昊，郭豪豪，Jay N Meegoda，董晓强

(1.清华大学 水利水电工程系 水沙科学与水利水电工程国家重点实验室，北京 100084；2.北京交通大学 土木建筑工程学院，北京 100044；3.新泽西理工学院 土木与环境工程系，美国新泽西 07102； 4.太原理工大学 土木工程学院，太原 030024)

随着人类经济和社会的高速发展，目前人类环境面临许多新的科学与技术问题：土壤地下水污染日趋加重，环境污染修复工作任重道远；温室效应加剧，二氧化碳地下封存成为缓解温室效应的有效手段；全球能源需求不断攀升，页岩气等非常规资源是世界能源开采的重要发展方向。上述问题与地质岩土材料中的渗流密切相关。地质岩土材料是自然界最常见的多孔介质，多孔介质多相渗流特性的研究具有广泛的理论价值及应用前景。

地下水是水资源的重要组成部分，根据2020年《中国水资源公报》，全国供水量的15.4%来自地下水，其中浅层地下水占95.7%[1]，高效地修复被污染的地下水是环境岩土工程领域的重要课题。污染物在地下水中通常以溶质形式存在，其在地下水中的运动过程涉及对流、机械弥散、分子扩散和吸附等多种作用[2]；在采用曝气法等常用修复方法进行地下水原位修复的过程中，通常涉及土壤介质中的气液两相运动，以及物质扩散、溶解、挥发、吸附等传质问题[3]；近年来纳米材料作为一种新兴的环境修复材料也开始被应用到地下水的原位修复当中，以纳米铁为代表的纳米修复材料在地下水中的有效粒径通常处于胶体的尺寸范围[4-6]。上述溶质、气液两相流、胶体在地下水中的运移主要存在于毫米-微米尺度的孔隙中。

随着经济社会的不断发展，化石能源不断燃烧导致大量的二氧化碳气体被排入大气，人类逐渐面临着海平面上升、全球气候变暖等全球性气候问题，我国也提出了“碳中和”与“碳达峰”的目标[7]。目前，二氧化碳地质封存是减少二氧化碳排放的重要手段之一，该方法是指将二氧化碳转变为超临界体并将其注入深部地层中进行长期储存[8]。超临界状态二氧化碳具有液相较高的密度，同时又保持气相较低的粘滞系数，在岩体孔隙中复杂的两相渗流和温度、力学和化学反应等形成了多场耦合作用。二氧化碳通常封存于地下岩层中，其孔隙尺度在微米量级。

作为一种非常规的化石能源，页岩气的开采已有200年的历史[9]，是世界能源的新领域[10]。页岩储层的孔隙尺度处于纳米尺度，页岩气、孔隙水以及劈裂液的多相流动以及气压变化导致储层压缩、渗透率降低产生了多场耦合复杂过程；页岩储层的高压、高温特性进一步使页岩气流动呈现出非达西流动的特征，准确预估页岩气产量、优化开采设计成为该领域的研究难点[11]；页岩气储层渗透率低，具有较好的密封特性，近年来有学者提出采用二氧化碳驱替页岩气，同时实现页岩气开采与二氧化碳地质封存[12]。

上述问题涉及的孔隙流体运动、物质运移等物理现象，与多孔介质孔隙结构以及多相渗流特性密切相关。传统的多孔介质渗流研究多集中于宏观物理现象的唯象描述与概化模拟，对于其微观机理与物理本质的研究尚不完善。基于连续介质假设的宏观模型忽略岩土介质的微观孔隙结构特性，通过设定宏观参数来概化岩土介质复杂的微观特性，无法反映微观尺度下的多相渗流、阻滞、弥散、指进效应等现象。岩土介质的渗流特性与其孔隙微观结构密切相关。近年来，多孔介质孔隙结构模型(Pore Structure Model)得到了发展，区别于传统宏观模型中对多孔介质为理想连续体的假设，孔隙结构模型将多孔介质中的固相骨架以及固相骨架之间的孔隙空间加以区分，并基于多孔介质中复杂的孔隙结构对渗流问题进行分析和计算。

按照对孔隙结构的描述及渗流计算方法由难到易，可以将目前常用的孔隙结构模型分为孔隙重构模型(Pore Structure Reconstruction Model)、孔隙网络模型(Pore Network Model)和等效孔隙网络模型(Equivalent Pore Network Model)三种。孔隙重构模型是对真实多孔介质内部的孔隙结构进行重构，并直接求解渗流控制方程；孔隙网络模型是在孔隙重构模型的基础上对孔隙结构中的孔隙和孔喉单元进行区分，从而对其中渗流计算进行简化；等效孔隙网络模型则是在孔隙网络模型的基础上进一步将孔隙排列在规则网格格点上，基于多孔介质孔隙特征统计参数建立简化的等效模型。本文将对孔隙重构模型、孔隙网络模型和等效孔隙网络模型的特点、构建方法以及在渗流分析方面的应用情况进行总结，梳理该领域亟待解决的问题和孔隙结构模型未来发展前景，为相关研究的开展提供参考。

1 孔隙重构模型

孔隙重构模型是指借助数值模拟或计算机图形学等手段，对实际岩土介质所占据空间中的固相骨架和孔隙结构的位置进行数字化，进而以孔隙结构作为边界，采用数值模拟的方法对渗流过程控制方程进行直接求解的模型。孔隙重构模型是对实际岩土介质孔隙结构的直接重现，对孔隙结构的刻画较为精细，同时由于其求解过程是在连通的复杂孔隙区域内进行直接的计算，计算代价通常较大，主要应用于较小的计算尺度。

1.1 孔隙重构模型的建立

目前建立孔隙重构模型的主要手段包括离散元重构法和序列图像重构法两种。离散元重构法是基于颗粒材料的粒径级配、孔隙率等基本参数对多孔介质的空间结构进行模拟，主要适用于粗粒土；系列图像重构法则是针对特定样本进行扫描，基于一系列二维的数字图像对其三维孔隙结构进行重构的方法，不仅适用于粗粒土，也适用于岩石。

1.1.1离散元重构法

离散元重构法是指通过离散元软件对一系列颗粒进行堆积，以模拟一定粒径级配、孔隙率、阻尼和摩擦角等参数条件下粗颗粒岩土介质的孔隙结构。在该方法中通常采用规则的球形颗粒[13]，其示意图如图1所示，也有学者基于真实粗粒土颗粒的形态来进行堆积[14]。在堆积完成后，则可以获得结构中任意颗粒的位置及所占据的空间，即获得多孔介质中固相骨架及孔隙的空间结构。离散元重构法对于砂土等颗粒本身接近球体并且具有较好连通性的粗粒土多孔介质材料具有较好的适用性，对于黏土、岩石等低连通性多孔介质材料则适用性较差[15]。

图1 离散元重构法构建的多孔介质空间结构Fig.1 Discrete element method to simulate the spatial structure of porous media

1.1.2序列图像重构法

序列图像重构法是基于成像技术获取岩土材料样本的一系列二维扫描图像，再通过计算机图形学方法将二维图像重构为三维数字图像[16]，该技术不仅适用于粗粒土同时也适用于页岩等岩石样本，岩石样品重构后的三维数字图像也称为数字岩芯[17-18]。目前常见的成像方法主要包括计算机断层扫描(CT)成像技术和聚焦离子束扫描电镜(FIB-SEM)成像技术[19]。CT成像技术是通过发射端发射X射线，穿过岩土介质时不同类型介质会对射线产生不同程度的衰减，由接收端接收后还原得到各位置的衰减系数，生成该扫描面的CT扫描图像[20]，典型的粗粒土CT扫描图像如图2(a)所示；FIB-SEM成像技术则是通过镓离子束对岩土介质样本进行连续切割，同时在电子束下成像的技术，该方法相比于CT技术具有更高的分辨率，更适用于页岩等孔隙尺寸在纳米级的岩土介质的研究[21]，采用FIB-SEM法获得的页岩二维数字图像如图2(b)所示[22]。

通过上述方法获得的二维图像通常含有噪声信息不能直接应用，因此需要经过滤波、闭运算、二值化等过程进行预处理提高图像精度。经过预处理的二维数字图像则可以经过规格化、像素值插值以及三维图像分割等步骤获得重构的三维多孔介质空间结构[23]。图2(c)展示了一组粗粒土的CT图像重构结果，图2(d)展示了一组页岩的FIB-SEM图像重构结果[22]。

1.2 基于孔隙重构模型的渗流分析

基于上述方法建立多孔介质孔隙重构模型后，可以对其中孔隙中的渗流问题进行分析和计算，该问题实为复杂边界条件下渗流方程的求解问题。目前常用的方法包括计算流体力学方法(CFD)和格子玻尔兹曼方法(LBM).

CFD是流体力学数值模拟的常用方法，该方法基于流体的连续介质假设，通常以欧拉方程和纳维-斯托克斯(N-S)方程作为控制方程，基于包括有限差分、有限体积、有限单元、有限分析和边界元等离散方法对控制方程进行求解[16]。ZHANG et al[25]基于CT图像对透水混凝土内部的孔隙结构进行了重构，并对渗流过程进行了模拟和分析；SANEMATSU et al[26]基于CT图像获得了砂岩样本内部的孔隙结构，并采用有限元法求解了其中的流场，基于流场计算结果采用拉格朗日粒子追踪法对其中纳米颗粒的运移和滞留行为进行分析。由于CFD模型的计算精度很大程度上依赖于网格划分精细程度，因此对于复杂孔隙结构的计算代价通常较大。

图2 基于序列图像重构法获取的多孔介质孔隙结构Fig.2 Spatial structure of porous media obtained by sequential image reconstruction method

LBM方法是一种介于流体微观分子动力学与宏观流体力学分析之间的计算方法，该方法将流体离散成介尺度的流体粒子，并通过粒子的平衡态分布函数特性计算其宏观渗流力学特征，对于复杂边界的计算求解问题有较大的优势[27]，目前被广泛应用于多孔介质渗流问题细观尺度研究。针对球堆积孔隙重构模型，刘一飞等[13]采用LBM研究了多孔介质粒径级配对土体渗透系数的影响；LONG和HILPERT[28]采用LBM对其中胶体的收集过程进行了模拟。刘振宇和吴慧英[29]基于CT图像对砂岩样本中的孔隙结构进行了重构，并基于LBM对其中气液两相渗流过程进行了研究。研究表明LBM方法能够对复杂边界条件下的多种多孔介质渗流问题进行有效求解。

2 孔隙网络模型

基于多孔介质孔隙重构模型进行渗流分析时，需要针对复杂的三维边界条件求解渗流控制方程，计算代价通常较大。为了提高计算效率，研究者们提出了孔隙网络模型的概念[30]。孔隙网络模型的核心思想是将孔隙结构简化为孔隙和孔喉的组合[31]，通常将孔隙结构中膨大的空腔定义为孔隙，将其中狭长的通道定义为孔喉，通常可以采用球体代表孔隙、用圆柱体代表孔喉[32]，其示意图如图3所示，也有研究采用立方体和棱柱体分别代表孔隙和孔喉，以描述在边角处的毛细作用[17]。经过上述简化，孔隙结构分解为大量规则的孔隙和孔喉，从而形成由孔隙和孔喉组成的网络，可以在此基础上进行渗流过程分析。

图3 孔隙网络模型示意图Fig.3 Schematic diagram of pore network model

2.1 孔隙网络模型的建立

在多孔介质孔隙重构模型的基础上，通过一定的几何规则对孔隙和孔喉进行区分，该过程称为孔隙结构提取。目前常用的孔隙结构提取方法包括四面体剖分法、居中轴线法和最大球法等。

2.1.1四面体剖分法

四面体剖分法适用于粗粒土，该方法将孔隙结构模型中所有固相颗粒看作其球心或颗粒质心的代表点，采用Delaunay四面体法对整个模型中的全部代表点进行四面体剖分，该剖分方法可以保证任意四面体的外接球不包含其余的点，以此保证所得的四面体均为最接近顶点所组成的四面体[33]，图1所示的颗粒堆积体所对应的四面体剖分结果如图4(a)所示。

在完成四面体剖分后，针对每一个四面体，可以确定位于该四面体顶点处的四个颗粒的最大内切球作为孔隙，进而获得孔隙的半径和位置信息，如图4(b)所示。对于规则球体堆积得到的孔隙结构模型，可以直接利用固相颗粒的半径和位置关系确定其最大内切球，而对于不规则固相颗粒堆积体或由序列图像重构得到的孔隙结构模型，由于其中固相颗粒形状不规则，则对其最大内切球的确定需要利用极值搜索方法进行，该过程应遵循如下原则：①内切球的球心应位于剖分得到的四面体内；②当内切球与任一位置颗粒接触时，即得到该处的内切球大小；③内切球的位置与半径应取为实数[23]。

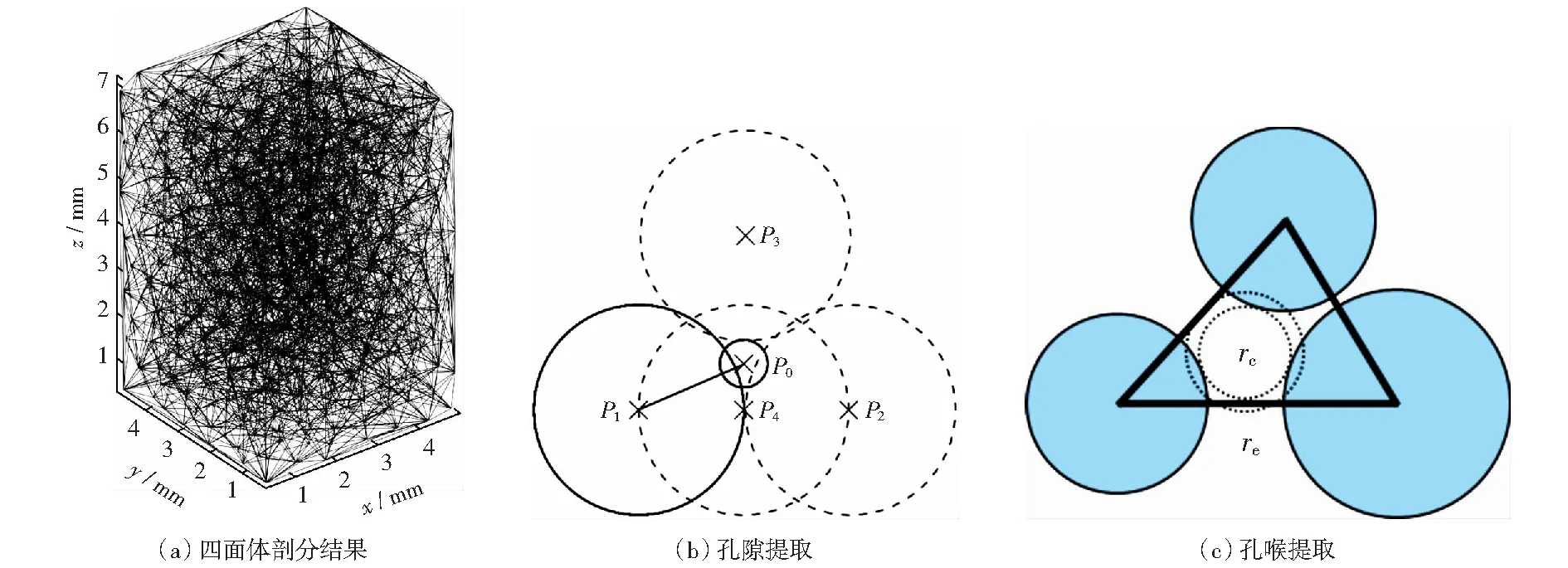
图4 基于四面体剖分法的孔隙结构提取Fig.4 Pore structure extraction based on tetrahedral subdivision method

在孔隙网络模型中，相邻孔隙间利用3个固相颗粒围成的通道进行渗流，因此由这3个固相颗粒形成的通道即为孔隙间的孔喉。BRYANT et al[33]提出了孔喉面积的等效计算方法，如图4(c)所示，其中rc表示3个球形成的横截面内的内切圆半径，re表示与截面中空隙部分渗流面积相等的圆半径，将二者的均值定义为等效的孔喉半径，基于上述方法可以确定孔喉的半径。

2.1.2居中轴线法

居中轴线将多孔介质孔隙结构看成形状不规则的连通管道，并将管道中轴线相连所构成的网络做为该孔隙结构的居中轴线，通常可以采用缩减算法[34]或烈火模拟算法[35]得到，图5展示了一组基于真实岩心样本所提取得到的居中轴线图[36]。基于居中轴线进行合理的分割和简化可以得到孔隙网络模型，通常将中轴线之间的节点定义为孔隙，将中轴线上孔隙空间的局部最小区域定义为孔喉[37]。AL-RAOUSH和WILLSON[38]细化了基于居中轴线法的孔隙识别方法，将居中轴线连线的交点作为孔隙中心，并采用膨胀法在该中心放置逐步增大的圆球，直到圆球接触岩石骨架，基于该方法确定了孔隙的半径。赵秀才[39]对居中轴线法进行了进一步的优化，对提取得到的枝节路径和冗余边界节点进行了处理。

图5 LINDQUIST et al[36]采用居中轴线法提出的孔隙网络模型Fig.5 Pore network extracted via medial axis method by LINDQUIST et al[36]

2.1.3最大球法

最大球法最早由SINGH和MOHANTY[40]提出，后续学者对该方法进行了进一步的发展和完善[41-43]。对于孔隙结构模型中孔隙空间中的任意一点，可以寻找以该点为球心并且与固相骨架相切的最大内切球，在去除包含在企图内切球中的冗余球体后，则可以获得能够描述孔隙空间的全部无冗余内切球的集合，并将其中局部半径最大的内切球半径定义为孔隙半径，将两个孔隙中局部半径最小的内切球半径定义为孔喉半径[44]，其示意图如图6所示。

2.2 基于孔隙网络模型的渗流分析

在采用上述方法对孔隙结构模型中的孔隙和孔喉进行区分后，则可以将边界形状复杂的孔隙结构模型转化几何形状规则的孔隙网络模型。根据图1所示球体堆积模型的孔隙结构，可以得到对应的孔隙网络模型如图3所示。

图6 采用最大球法提取得到的孔隙和孔喉Fig.6 Pore body and pore throat extracted by maximum sphere method

利用孔隙网络模型，可以简化多孔介质孔隙结构渗流问题的计算分析。对于单相渗流问题，由于多孔介质中的渗流过程主要由模型中狭窄的通道控制，因此通常假设孔隙网络模型中的单个孔隙中压强处处相同，流入每个孔隙的流量应符合质量平衡；孔喉两端连接的孔隙压强可以不同，其中的渗流过程可以用Hagen-Poseuille管流公式计算[45]，从而使研究者免于对复杂边界条件下的渗流方式进行求解，极大提高了计算效率。

基于上述研究思路，研究者们基于孔隙网络模型开展了多孔介质中单相渗流、两相流及溶质运移等问题的研究。GAO et al[45]构建了等直径球体简单立方堆积条件下所对应的孔隙网络模型，并基于该方法研究了不同粒径条件下多孔介质孔隙结构的渗透系数，计算结果与文献中的试验结果较为接近；GONG和PIRI[46]构建了基于CT扫描图片重构的岩心结构所对应的孔隙网络模型，并在饱和及非饱和条件下对该岩心中的溶质运移问题进行了研究；杨永飞等[47]基于数字岩心构建孔隙网络模型，研究了页岩试样中的孔隙结构特征及油相流动能力。

3 等效孔隙网络模型

孔隙网络模型孔隙及孔喉基于实际孔隙结构建立，其拓扑结构较为复杂。针对多孔介质孔隙结构中的孔隙尺寸、孔喉尺寸、孔隙与孔喉的连接情况、孔隙率等数据进行统计分析，可以获得不同类型多孔介质材料孔隙结构的特征参数取值范围。一般认为，当多孔介质孔隙结构的特征参数相同时，其渗流特征具有相似性。基于上述思路提出等效孔隙网络模型，该模型与孔隙网络模型的区别在于该模型的建立不依赖于具体的多孔介质样本，而是基于描述多孔介质孔隙结构特征的特征参数，将孔隙排列在一定规则的网格顶点上，并生成孔隙之间连接的孔喉，从而实现对孔隙结构模型拓扑结构的简化。

3.1 等效孔隙网络模型的构建

构建等效孔隙网络模型，首先需要对描述多孔介质孔隙结构特征的参数进行定义和分类统计，之后将根据特征参数的取值，生成不同类型的等效孔隙网络模型。本文基于球形孔隙及圆柱形孔喉的等效孔隙网络模型的相关特征进行介绍，也有学者采用立方体及棱柱体作为孔隙和孔喉进行模拟[48]。

3.1.1描述多孔介质孔隙结构的特征参数

基于球形孔隙和圆柱形孔喉的基本假设，可以用如下参数来描述多孔介质孔隙。

1) 孔隙半径：多孔介质中膨大的空腔为孔隙，当用球体对孔隙进行描述时，对应的球体半径则记为孔隙半径。

2) 孔喉半径：多孔介质中狭长的通道为孔喉，当用圆柱体对孔喉进行描述时，对应的圆柱体半径记为孔喉半径。

3) 孔喉长度：描述孔喉的圆柱体的长度记为孔喉长度。

4) 孔隙率：多孔介质中孔隙和孔喉的总体积为孔隙体积，孔隙体积占多孔介质总体积(孔隙体积+固相体积)的比例为孔隙率。

5) 配位数：配位数是指一个孔隙连接的孔喉数量。

在多孔介质孔隙结构中，每一个孔隙、孔喉的尺寸以及配位数均可能不同，因此除孔隙率这一宏观参数外，孔隙半径、孔喉半径、孔喉长度及配位数在多孔介质中均有一定的分布特征。对于页岩等具有较强各向异性的多孔介质，其配位数的分布在不同方向上也存在显著差异。

张鹏伟[15]通过文献调研对不同类型岩土介质孔隙特征参数进行了总结，指出对于砂土、砂岩及页岩3种岩土介质，其孔隙尺寸由毫米级别逐渐过渡到纳米级别，其孔隙连通性也逐渐由高向低转变，文献中所述的上述3种岩土介质的平均配位数范围如表1所示。

表1 不同岩土介质的平均配位数取值范围Table 1 Value range of average coordination number of different porous media

3.1.2等效孔隙网络模型的构建

基于上述孔隙特征参数的统计结果，研究者们建立了不同类型的等效孔隙网络模型。FATT[49]最早基于毛细管模型提出了采用二维蜂窝状网格、规则方形网格、双重六边形网格以及三重六边形网格的二维等效孔隙网络模型，并利用上述模型对基质吸力曲线进行了模拟。后来的研究者将上述思路拓展到了三维情况[50-51]，例如REEVES和CELIA[52]将孔隙排列在立方体网格的格点上建立了三维等效孔隙网络模型，上述文献中所报道的孔隙网络模型的配位数是恒定的，取决于所采用的网格类型。也有学者将等效孔隙网络模型称为非重建模型[16]或规则拓扑孔隙网络模型[18]。

RAOOF和HASSANIZADEH[53]提出了最大配位数为26的等效孔隙网络模型，将孔隙排列在立方体网格的格点上，每一个孔隙最多与周围的26个孔隙相连，并且基于配位数的正态分布随机生成每个孔隙与周围孔隙的连接关系，更充分地考虑了孔隙连通的多向性和无序性。张鹏伟[15]基于最大配位数为26的等效孔隙网络模型，通过考虑配位数在不同方向的连接比例，建立了能够反映各向异性的等效孔隙网络模型，并对不同岩土介质的渗透率进行了计算，验证了该模型的有效性，并将模型应用到了页岩气开采和二氧化碳注入页岩过程中的水气两相流模拟中。上述等效孔隙网络的结构示意图如图7所示。

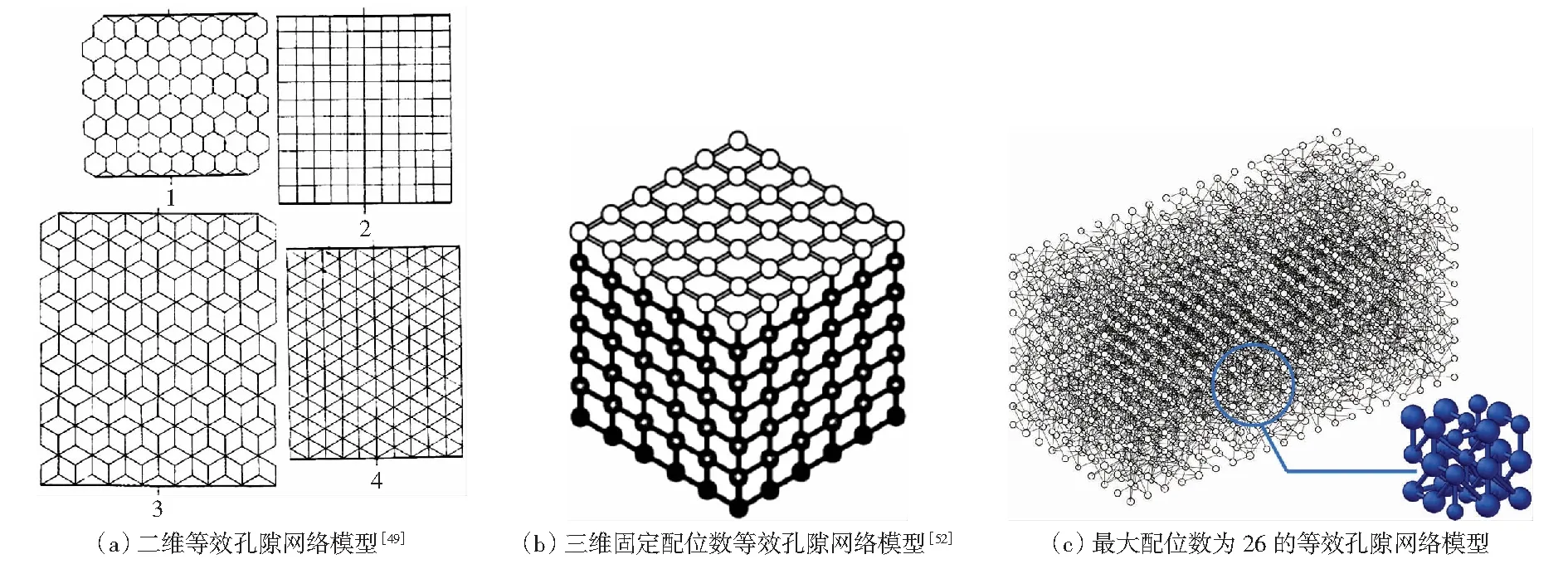
图7 等效孔隙网络模型示意图Fig.7 Schematic diagram of equivalent pore network model

3.2 基于孔隙网络模型的多相渗流和物质输移问题分析

基于等效孔隙网络模型，研究者们对多孔介质中的气液渗流、溶质运移、胶体运移等问题进行了研究。

3.2.1渗流分析

基于页岩等岩体的孔隙结构统计参数的取值范围，ZHANG et al[54]构建了等效孔隙网络模型描述页岩孔隙连通情况及低渗透性，同时综合考虑了气体在纳米尺度孔隙中的Knudsen扩散及滑移流作用，研究了不同压力条件下页岩气渗流过程，结果表明页岩气的表观渗透率与孔隙压力显著相关，随着页岩储层压力的降低滑移流和克努森扩散逐渐占主导地位，页岩气流动存在明显的指进效应，如图8所示；进一步考虑页岩的各向异性进行计算分析，通过与试验结果的比较，进一步验证了等效孔隙网络模型在渗流模拟上的有效性[55]；此外，ZHANG et al[56]还基于等效孔隙网络模型研究了二氧化碳地质封存和页岩气开发耦合过程中二氧化碳与甲烷的竞争吸附过程。

3.2.2溶质运移分析

RAOOF et al[57]发展等效孔隙网络模型描述多孔介质中溶质运移过程，考虑溶质随着孔隙水的对流作用，以及由于多孔介质复杂孔隙流场引起的机械弥散作用，并研究了饱和度对溶质运移过程的影响[58]；张兴昊等[59]在此基础上考虑了溶质分子扩散作用，计算结果表明孔隙结构参数对水动力弥散过程有显著影响，在高流速条件下水动力弥散系数与机械弥散系数接近，在低流速条件下水动力弥散系数与分子扩散系数接近，而在中等流速的过渡阶段，水动力弥散系数小于机械弥散系数与分子扩散系数的和，如图9所示，其原因是分子扩散作用导致溶质在低流速区域的运移。

3.2.3胶体运移分析

近年来，等效孔隙网络模型也逐渐被应用到胶体运移和滞留的研究领域。YANG和BALHOFF[60]建立了带有收缩管孔喉的等效孔隙网络模型，并利用粒子追踪的方法研究了其中胶体的运动过程；SEETHA et al[61]建立了带有圆柱形孔喉的等效孔隙网络模型，并提出了孔喉尺度沉积速率的表达式；LIN et al[62]发展了能描述胶体运移和滞留过程的等效孔隙网络模型，模型中考虑了多孔介质固相表面粗糙度和化学异质性对表面沉积过程的影响作用和对胶体出流和滞留曲线的影响，结果表明胶体的收集效率系数、粘附效率系数、最大沉积面积比等描述胶体运动的孔隙参数在多孔介质存在一定的空间分布特征[62]；通过训练神经网络模型实现对胶体的收集效率系数的快速计算，并基于等效孔隙网络模型建立了从孔隙参数到宏观运移参数的升尺度计算方法[63]，此外，在等效孔隙网络模型计算分析中考虑了表面沉积、筛滤作用及粒桥3种滞留作用，研究在不同胶体粒径、注入浓度及流速条件下胶体的宏观出流及滞留曲线的变化趋势，结果表明仅考虑表面沉积作用产生均匀的滞留曲线，而同时考虑粒桥作用则可以重现试验中胶体在入口处大量滞留的超指数型滞留曲线，如图10所示[64]。

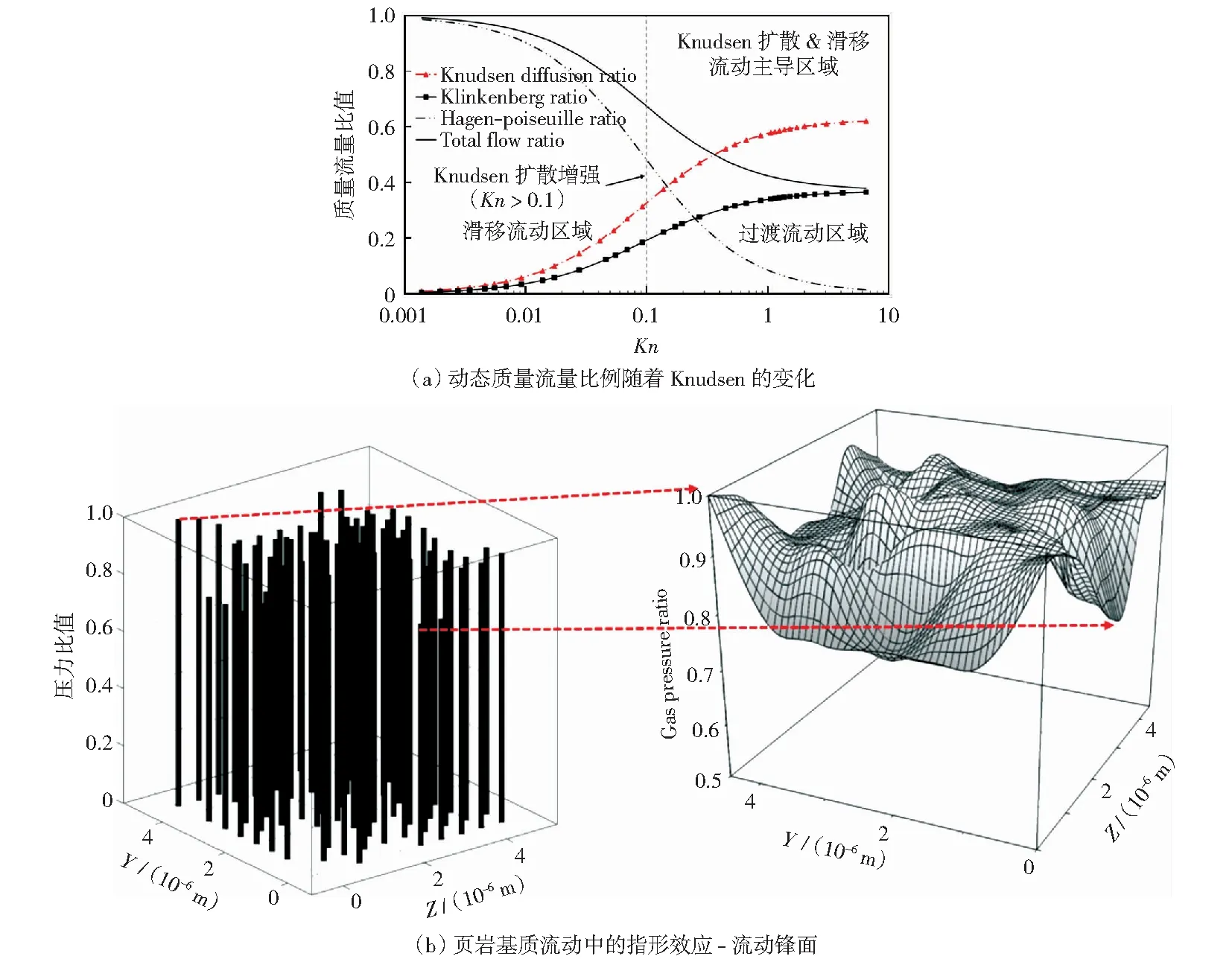
图8 页岩多流态计算结果及指进效应[54]Fig.8 Calculation results of shale multi-flow states and fingering effect[54]

D为水动力弥散系数，D*为机械弥散系数，D′为分子扩散系数图9 不同孔隙流速条件下对应的弥散系数Fig.9 Corresponding dispersion coefficient under different pore velocity

4 结论与展望

本文将多孔介质孔隙结构模型分为孔隙重构模型、孔隙网络模型和等效孔隙网络模型，分别介绍了3种模型的概念、建立方法以及在渗流分析领域的应用。从孔隙结构模型到孔隙网络模型再到等效孔隙网络模型，模型对多孔介质孔隙结构的描述逐渐由真实性向等效性发展，同时计算效率则显著提高。孔隙结构模型对于研究渗流过程的微观机理具有重要作用，目前研究集中于多孔介质中渗流分析，包括气体和液体渗流、溶质运移和胶体运移等问题的数值模拟。

图10 胶体粒径对表面沉积和粒桥的影响[64]Fig.10 Effect of colloid size on surface deposition and particle bridging[64]

目前研究主要针对具体的岩土材料样本构建对应的孔隙结构模型。由于岩土材料孔隙结构复杂多样，今后的研究中应重视对不同类别岩土材料的多孔介质孔隙结构特征的统计分析，基于统计参数的等效性建立更具有普适意义的模型，提高计算分析效率，深入认识多孔介质渗流和物质输移过程孔隙尺度的物理机理。同时，随着孔隙结构模型发展和计算效率提升，建立微观机理与宏观特征之间的内在联系和定量关系，进而基于多孔介质材料特征实现宏观渗流和物质输移行为的预测分析是未来的重要研究方向。