基于均衡学习的联邦推荐算法研究

苏 洋,张 浩,刘俊彤

(皖南医学院 医学信息学院,安徽 芜湖 241002)

随着互联网的快速发展,用户难以从海量信息中快速搜索到所需的信息,信息过载问题日益严重,个性化推荐系统[1]是一种有效的解决方法,其中协同过滤是目前使用最广泛的一类推荐算法。通过对用户过往数据进行分析,得到用户的偏好,从而对其完成推荐,具有不需要领域知识、工程上实现简单等优点[2]。

推荐系统性能的优劣很大程度上取决于训练数据质量的高低,当数据量较少,数据稀疏性较大时,推荐系统的性能较差。同时现实情况下数据往往分属于不同的数据持有者,数据孤岛[3]现象十分严重。此外,这些数据包含了大量的用户隐私,近年来国内外纷纷在法律法规层面上进行保护,对于用户数据隐私的保护日益规范[4]。因此,如何在保护数据隐私的前提下,联合多方共同进行推荐模型训练是推荐系统的一个研究热点。联邦推荐算法是其中的一个重要研究方向。

目前关于联邦推荐系统的研究主要集中在数据隐私安全、模型聚合方式和通信方式等方面,对于博弈论在其中的研究相对较少。然而在联合模型训练中,推荐的效果不仅取决于自己提供的数据,很大程度上也依赖于其他客户端提供的数据,这就导致各客户端在联合训练中存在博弈,即期望己方提供较少的数据,期望对方提供更多的数据。本文采用博弈论[15]的方法对联邦推荐系统中的各客户端之间的行为进行分析讨论。

文献[16]使用博弈论对传统协同过滤推荐系统中各用户的评分行为进行了分析。在该文中,用户对体验过的项目进行评分会产生相应的代价,因此用户不会对所有项目都进行评分并将数据提供给服务器,故将评分数据提供给服务器这一行为视为用户的策略。此外,该文认为每个用户对于推荐效果均有一个心理预期,当未达到预期时,倾向于提供更多的数据以使推荐效果进一步提升;当达到预期时,倾向于不再提供更多的数据。在此基础上,该文提出了一种基于用户数据迭代更新策略的算法。

本文针对数据分布于各客户端的情况,提出了一种基于均衡学习的联邦推荐算法(federated recommendation algorithm based on equilibrium learning,FRER)。将各客户端进行本地模型训练时提供的数据量作为用户策略,由于在联邦学习训练过程中,各客户端无法得知其他客户端采取的行动,将各客户端之间的交互建模为不完全信息博弈。同时,本文假定各客户端对于推荐效果有一个预期,当最终的推荐效果高于预期时,达到满足状态。因此，本文采用满足均衡(satisfaction equilibrium)的概念来分析该博弈的均衡。为使该博弈能够达到均衡状态,本文采用均衡学习方式对策略进行调整,在每一轮训练中,各客户端根据上一轮训练时是否达到满足状态,动态调整进行本地模型训练时的数据量。为验证所提算法的有效性和可行性,本文进行了算法收敛性的理论分析,并通过一系列仿真实验对理论分析的结果进行了验证。

1 博弈模型

1.1 场景描述

将评分矩阵Rl×m分解成Pl×k和Qk×m,其中:Pl×k为用户隐向量矩阵;Qk×m为项目隐向量矩阵;k为隐向量维数。对于某一个用户评分rui,可以用(1)式进行评分预测。

(1)

(2)

bu←bu+γ(eui-λbu)

(3)

bi←bi+γ(eui-λbi)

(4)

pu←pu+γ(euiqi-λpu)

(5)

qi←qi+γ(euipu-λqi)

(6)

(7)

在上述计算中,各客户端利用数据在本地进行模型训练,计算出用户隐向量和用户偏好偏置,将项目隐向量和项目偏置上传至服务端进行模型参数聚合,从而在保证数据隐私的前提下,完成联合建模。本文规定,每轮迭代之后,各客户端会计算当前模型是否达到期望的推荐效果,即是否达到满足,并根据计算结果,选择下一轮迭代时提供的数据量。

1.2 满足均衡博弈

(8)

(9)

本文用gi(M)表示上一时刻训练结束后客户端ci的模型推荐效果,M表示本地模型,当gi(M)≥Γi时,表示客户端ci达到满足状态。然而gi(M)只是从单个客户端方面对模型性能进行了描述,不能很好体现模型性能与其他客户端之间的联系,因此通过引入数据完整度θ和映射函数f,可将gi(M)改写为f(θi,θ-i;pi)。f(θi,θ-i;pi)表示以θi和θ-i作为输入,以pi为参数,可以更直接地表示客户端ci的推荐效果不仅与自己提供的数据有关,也和其他客户端提供的数据密切相关,同时自身提供的数据量也会影响其他客户端提供的数据量。为此,定义函数ψi(θ-i)为客户端ci在θ-i状态下选择θi的关系。基于此,本文用(11)式定义所建立的博弈模型。

ψi(θ-i)={θi∈Αi:fi(θi,θ-i)≥Γi}

(10)

G=〈C,{Αi}i∈C,{ψi}i∈C〉

(11)

2 基于均衡学习的联邦推荐算法

在上文建立的博弈模型中,直接分析该博弈的均衡是很困难的。一种可行的方法是设计某种行为规则,让客户端在迭代交互的过程中依据该规则不断调整自己的策略,最终学习到一种均衡策略。

结合联邦推荐系统的工作原理,本文设计了一种学习算法,该算法允许客户端以逐渐增加训练数据的方式寻找均衡策略。本节首先介绍算法的基本流程,然后对算法的收敛性进行分析。

2.1 均衡学习算法

在无线通信网络中,文献[18]针对服务质量(quality of service,QoS)问题,设计了一种基于满足均衡算法的迭代方法。本文将这种方式应用于联邦推荐系统之中。

在联邦推荐系统中,客户端与服务器端的交互是长期的,客户端不断向服务器端提供本地模型的参数,服务器端则进行模型参数聚合不断调整全局模型并反馈给各客户端。本文中,客户端根据当前推荐效果动态调整本地模型训练的数据,客户端与服务器端的交互如图1所示。

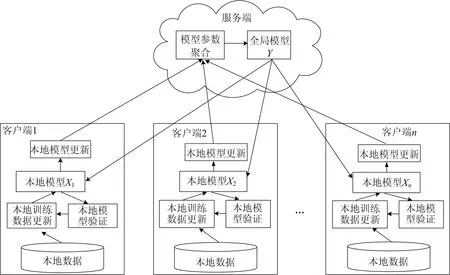
图1 客户端与服务器端交互示意图

各客户端在与服务器迭代交互的过程中按如下规则行动:

初始时刻(t=0),客户端选择部分本地数据进行模型训练,参与联合建模。当服务器端完成模型参数聚合,并回传给各客户端后,各客户端计算当前模型的推荐效果是否已达到预期,以变量vi(t-1)表示，即

(12)

(13)

(14)

当所有客户端完成数据选择、本地模型训练后,服务器端对bi、qi进行聚合并回传给各客户端进行推荐性能测试,之后再进入下一轮迭代。若经过ns(ns>0)次迭代之后,对于期望的推荐效果Γ,所有客户端都得到了满足,则迭代终止,称学习过程收敛于满足均衡。将上述行为规则归纳为算法1,描述如下：

Input:Mclients, ServerS

S:initializebi,qi

while iteration conditions true do

for each clientm∈Mdo

ift=0 do

initialize train data

else

calculategi(M(t-1))&vi(t-1) using eq.12

update train data using eqs.8,13-14

endif

updatebu,bi,pu,qiusing eqs.3-6

transferbi,qitoS

endfor

S:updatebi,qiusing eq.7

endwhile

returnbu,bi,pu,qi

2.2 收敛性分析

随着迭代的进行,可以看出模型训练的数据量必然呈现出增长的趋势,最终可以使所有客户端均达到满足状态(即∀ci∈C,ci=Ps),使算法完成收敛,3.2节给出了实验验证。

3 实验仿真

为了验证算法1的可行性,本文使用Movielens数据集进行一系列仿真实验。本节首先对实验所用的数据集以及仿真参数的设置进行说明,然后对不同参数设置下的仿真结果进行分析, 最后对算法收敛条件进行验证。

3.1 数据集和参数设置

Movielens数据集是推荐系统中的经典数据集,由明尼苏达大学搜集整理而成,本文选用了MovieLens 1M Dataset①http://files.grouplens.org/datasets/movielens/ml-1m.zip进行实验仿真,包含了6 040名用户对3 952部电影的1 000 209条匿名评价。本文删除了评价数目低于100的用户数据,最终得到了2 945名用户对3 670部电影的847 302条评分数据,数据稀疏度为7.84%。

本文采用横向联邦学习架构,假定这些数据分布于5个客户端,故将数据从用户角度随机划分成5份,并将其中90%的数据作为训练数据,10%的数据作为测试数据,划分后各客户端拥有的数据量见表1所列。

使用平均绝对误差(mean absolute error,MAE)作为模型性能评价指标[19],用lMAE表示,即

(15)

表1 各客户端数据分布

图2 不同数据完整度下模型性能

(16)

(17)

各客户端对于η可能有不同的期望,本文考虑以下3种情况:

(1) 各客户端有较高期望。∀ci∈C,η=0.85。

(2) 各客户端期望一般。∀ci∈C,η=0.5。

(3) 各客户端期望不一。{c1,c2,η=0.85;c3,c4,c5,η=0.5。

不同情况下根据(17)式计算出具体的Γi，见表2所列。

表2 不同情况下各客户端Γi值

客户端对数据的重视程度α、获取数据的代价φ、达到满足状态后维持数据不变的概率σ都会直接影响算法1的性能,为尽可能地做出全面分析验证,本文对以上3个参数取值如下:α∈{1.5,2};φ∈{1,2};σ∈{0.9,1}。

除η、α、φ、σ外,本文还有以下参数设定:初始时刻,各客户端参与训练的数据完整度θ=0.25;客户端进行本地模型训练时,隐因子维度为100、学习率γ=0.005、正则化系数λ=0.02;当客户端达到满足状态后仍愿意提供更多数据的因子k=5。

3.2 仿真实验结果

为验证不同η下算法1的性能,本文设定α=2、φ=1、σ=0.9,实验结果见表3所列,可见3种情况下,算法均完成了收敛。

当各客户端均有较高期望时,算法收敛较慢,同时需要提供更多的数据才能达到均衡状态。以客户端c1为例,当η=0.85时,其在第23轮训练结束时达到满足状态,数据完整度为89.71%,而当其将期望降低,η=0.5时,在第13轮就达到了满足状态,同时只提供了73.61%的数据。

当各客户端期望不一时,相比于期望较低的客户端,期望较高的客户端的收敛速度明显较慢,同时需要提供更多的数据。以客户端c2和客户端c3为对比,c2在第29轮达到满足,c3在第4轮就已达到满足。同时对于c2来说,mix环境下需要提供更多的数据,当η均为0.85时,c2在mix环境下需要多提供5.77%的数据,而c3在η均取0.5的情况下,数据量减少12.95%。这说明在混合环境下,对于期望较高的客户端,为了达到预期效果,需要付出等多的代价,而期望较低的客户端在期望较高客户端提供更多数据的情况下,只需提供较少数据就可以实现预期。

表3 不同η取值下算法仿真实验结果

σ也是影响算法性能的重要因素,客户端c2在η=0.85、α=2、φ=1下,σ分别取0.9和1.0情况下的仿真实验结果如图3所示,从图3可以看出，2种情况下均达到了满足状态。与σ=1相比,σ=0.9时,客户端c2较快达到满足状态,同时,在满足后,客户端仍有可能提供更多的数据,这会导致最终模型性能更好。当σ=1时,客户端达到满足时,则不会再提供更多的数据,当所有客户端均达到满足状态时,即使随着迭代的继续进行,整个模型性能仍将不再变化。此外,从图3a可以看出,当客户端提供较少数据时,其在后续迭代中倾向于提供更多数据,然而当数据量较大时,则会倾向于维持现有数据量。

客户端对数据的重视程度α、获取数据的代价φ同样也是影响算法的因素,本文也进行了相实验验证。客户端c2在η=0.85、σ=0.9、φ=1下,α分别取1.5和1情况下的仿真实验结果如图4所示。客户端c2在η=0.85、σ=0.9、α=1下,φ分别取2和1情况下的仿真实验结果如图5所示。从图4、图5可以看出，当客户端对数据越重视(即α、φ取值越大)的情况下,模型最终的性能要逊于对数据不那么重视的情况(即α、φ取值越小)。

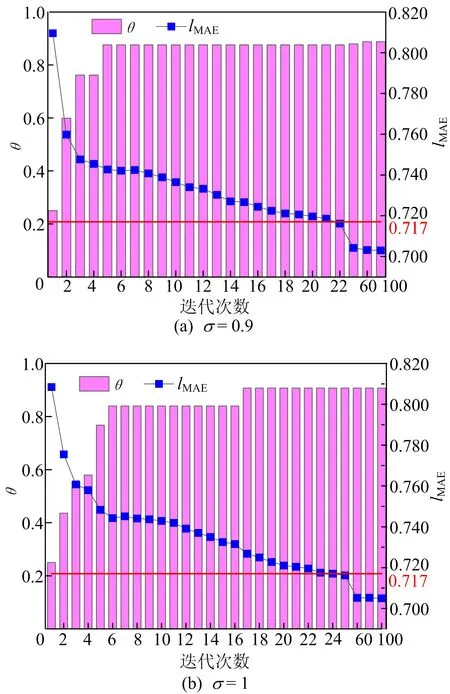
图3 客户端c2在不同σ下模型性能

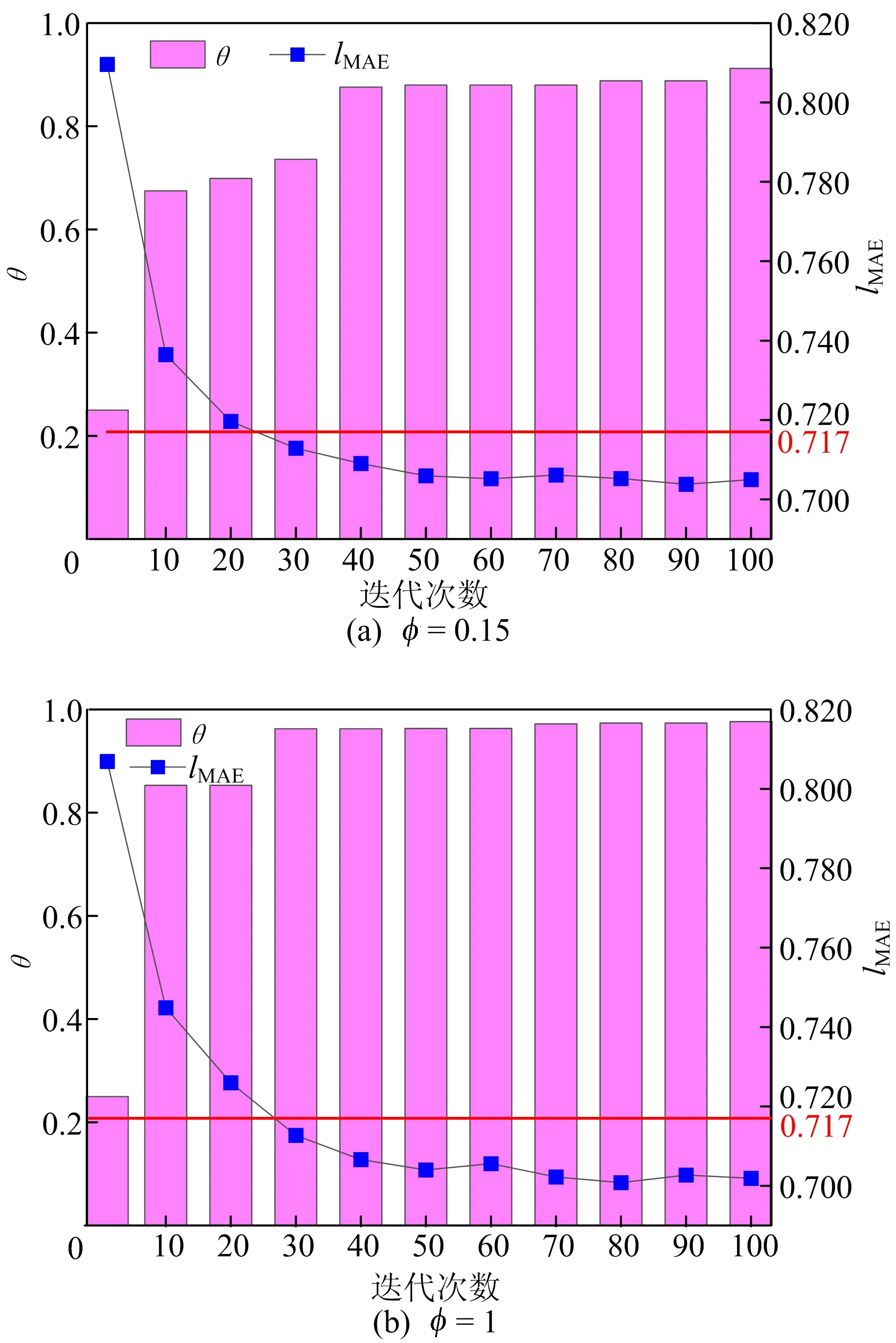
图4 客户端c2在不同α下模型性能

上述仿真实验测试了算法在不同情形下的运行状况,算法均在有限迭代次数内完成了收敛,表明算法具有较好的可行性和适用性。

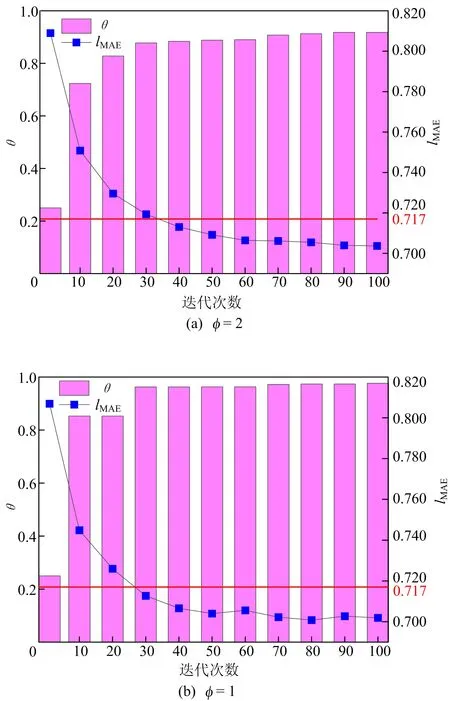
图5 客户端c2在不同φ下模型性能

4 结 论

联邦推荐系统中,各客户端相互协作共同训练推荐模型,然而由于数据获取需要付出一定的代价且出于对自身数据安全的保护,在能达到预期推荐效果的前提下,客户端倾向于尽可能少地提供自身数据,这使得在联合模型训练过程中,各客户端之间存在着博弈行为。本文利用博弈论相关概念对这一行为进行了分析将其建模为不完全信息博弈,并使用满足均衡解释该博弈,提出了一种基于均衡学习的迭代算法FRER进行求解。FRER允许各客户端在训练过程中可以根据上一轮训练结束后的推荐模型效果来动态地调整参与模型训练的数据,通过理论分析和仿真实验均表明了算法的可行性。

后续工作可将激励机制应用到联邦推荐系统中,刺激客户端提供更多的数据以使模型的性能进一步提升。将深度推荐学习算法应用到FRER中也是未来的一个重要研究点。