基于无人机倾斜摄影测量的树冠体积及表面积提取算法对比分析

王玉堂，王佳,2*，牛利伟，常书萍，孙露

(1. 北京林业大学林学院，北京 100083； 2. 北京林业大学精准林业北京市重点实验室，北京 100083)

树冠体积和表面积的传统计算方法主要是通过伐倒木解析或使用测绘工具测量树木的冠幅、冠高等参数，根据树冠形态将其拟合成近似的几何图形，根据相应的体积公式进行求解[1-2]。传统的计算方法费时费力，破坏性强，并且由于树冠结构的不规则性，传统方法计算精度不高，很难满足实际需求[3]。三维激光扫描技术具有高精度、穿透性、不接触性等特点，为了提高测量精度，许多学者将其引入树冠的测量中[4-5]。

近年来，无人机航空摄影测量技术兴起，广泛应用于地籍测绘、城市三维建模、土方量计算等多个领域。由于无人机遥感具有机动、灵活、低成本、安全性高等优势，不断发展成为林业调查中的主要手段[6-7]。其中正射影像结合树木三维点云可以精确地提取树木高度信息[8]，倾斜摄影测量能够快速、高效地获取树木不同角度的特征信息，真实地反映树木的三维结构[9]。基于视觉的三维重建技术不受物体形状及场景的限制，可快速实现全自动或半自动建模。其中，基于多视点的运动恢复结构(structure from motion, SFM)算法，利用不同角度并且具有一定重叠度的一系列影像数据，通过特征点匹配来求解相机姿态参数和变换矩阵，从而实现物体三维几何信息的恢复[10]。正是由于SFM算法的通用性，其不依赖于某一特定场景，所以无人机倾斜摄影测量的多角度特征与SFM算法相结合为林业调查提供了一种新思路。

曾健等[11]证明了使用无人机倾斜摄影测量和SFM算法生成的点云数据来提取落叶松人工林地形信息的可行性；Wallace等[12]对比分析了使用机载激光雷达(ALS)和SFM算法两种方法生成的树木点云数据，两种方法都可以提取树木特征信息，但ALS方法生成的树木点云点密度更高，林下信息更丰富，提取精度也更高。但由于在实际应用中三维激光扫描仪成本高操作复杂等缺点，并且在低郁闭度的林区两者林分信息的提取精度较为接近[13]，所以使用无人机倾斜摄影测量的多角度影像数据结合SFM算法进行的三维重建，是林分调查时的最佳低成本替代方法。

基于高精度点云数据提取树冠体积和表面积的算法有很多，应用较为广泛的主要有体元法[14]和数字高程模型法[15]。这两种算法都有其优缺点，体元法充分考虑了树冠内部空隙，但该方法无法区分树冠真实空隙和因遮挡而形成的伪空隙，而且在树冠表面规则性较差时不能很好地体现树冠的边缘特征，并且操作复杂计算过程较慢；数字高程模型法利用了点云数据的高程信息，并且结合数字化测绘数据处理系统生成立体三角网，操作方便快捷，还可以很好地反映树冠的边缘特征，但其进行计算时忽略了树冠内部的空隙，而且三角网容易出现过拟合现象。

本研究使用多旋翼航测无人机对北京市怀柔区主要道路的行道树进行倾斜摄影测量和树木模型的三维重建，在获取单木点云数据的基础上，对比分析两种树冠体积和表面积的提取算法在不同冠型、不同点云密度等方面的差异，以期为无人机倾斜摄影测量提取树冠体积和表面积的算法研究提供参考。

1 材料与方法

1.1 试验区概况

试验地位于北京市怀柔区(116°17′～116°63′E，40°41′～41°04′N)中心主干道，属于典型的北温带半湿润大陆性季风气候，夏季高温多雨，冬季寒冷干燥，春、秋短促，年均气温9～13 ℃，年均降雨量600～700 mm。试验区的行道树主要树种为洋白蜡(Fraxinuspennsylvanica)、侧柏(Platycladusorientalis)、银杏(GinkgobilobaL.)、美桐(PlatanusoccidentalisL.)、刺槐(RobiniapseudoacaciaLinn.)、毛白杨(Populustomentosa)等代表性树种。

1.2 数据获取

1.2.1 试验地选取

无人机飞行作业需远离强干扰物及高大建筑物等干扰物，并且由于研究精力有限，所选行道树要具有代表性，树木间遮挡较少，以便单木点云数据的准确提取。由于市区环境复杂，经过飞行前的实地考察，综合考虑以上因素后，在符合条件的区域选择了5段50 m长的道路作为实验地，路旁的行道树作为实验树种。

1.2.2 无人机数据获取

无人机飞行时间为2019年10月19日和20日，这两天天气晴朗风力较小。为避免光照条件对实验结果的影响，每天的飞行时间选为10：00和13：00 两个光照较好的时间段。为保证测量结果的准确性，防止倾斜摄影测量精度的不同对研究结果产生影响，本研究在实际测量每块样地时控制了变量的统一，保证了每次倾斜摄影测量的高度、倾斜角度以及飞行速度等参数不变。具体参数为：飞行高度30 m，航向重叠度80%，旁向重叠度70%，飞行速度为1 m/s。数据获取平台为大疆精灵4 RTK(公司：大疆创新；产地：中国深圳)行业级测绘无人机，无人机飞行航线示意图见图1(以样地4为例)。

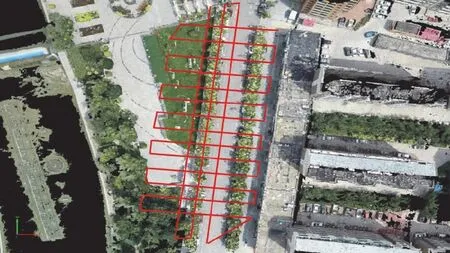
图1 无人机飞行航线Fig. 1 Schematic diagram of UAV flight routes

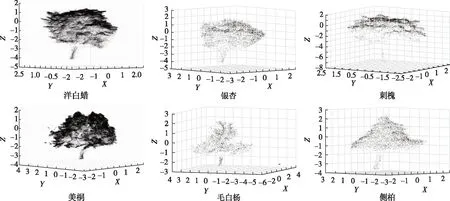
图3 单木点云图Fig. 3 Single tree point cloud

1.3 实验方法

利用摄影测量软件将航拍影像生成点云模型，并对点云数据进行去噪、单木分割、树冠提取等数据预处理操作，对处理好的点云数据分别使用体元法和数字高程模型法计算树冠体积和表面积，实验流程见图2。

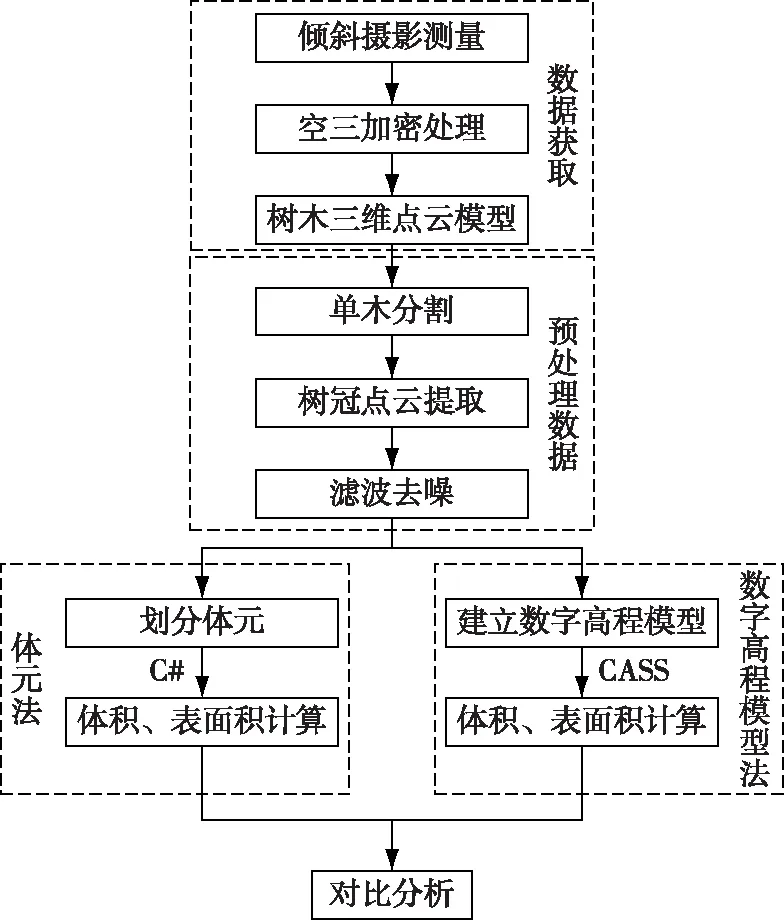
图2 实验流程Fig. 2 Experimental flow chart

1.3.1 数据预处理

1)选择Pix4D-mapper(版本号为2.0.104；公司为Pix4D；产地为瑞士洛桑)作为航拍影像处理软件，导入影像数据，软件自动读取照片位置信息。Taddia等[16]在实地实验中测试了DJI Phantom 4 RTK倾斜摄影测量数据在有像控点和没有像控点情况下的均方根误差(RMSE)，结果表明两者仅相差0.003 m。可以看出，无人机在RTK GNSS下不使用像控点和使用像控点时测量结果的误差非常小。同时，为了减小缺少像控点带来的误差，将飞行高度设为30 m。选择倾斜摄影测量建模方式，设置坐标系和投影，默认为WGS 84 / UTM zone 50N投影坐标系。软件自动进行初始化，提取并匹配特征点生成树木三维点云数据。

2)在Pix4D-mapper软件中的点云模式下，使用点云编辑工具人工手动进行单木分割(图3)和树冠部分点云的选取，并将分割好的树冠点云数据以.las格式进行输出。由于图片分辨率和航线重叠度较高，倾斜摄影测量生成的点云具有较高的质量，本研究生成的树木点云平均密度为5 043.8点/m3。

3)使用编程语言Python选择基于统计的方法，根据相邻点之间的距离来去除噪声点。

1.3.2 体元法计算树冠体积和表面积

体元法计算树冠体积和表面积的基本思想是将树冠划分成无数个小立方体，选择适合大小的体元就能很好地模拟出树冠形态及内部结构。先给树冠分层，以树冠的最高点和最低点连线作为Z轴，以k为间隔将树冠划分为n层，将每一层的点云投影到垂直于Z轴的XY平面，同样沿X轴和Y轴以k为间隔划分体元。根据韦雪花等[14]的实验可知，当体元边长k≤冠径/10时计算结果较好，计算用C#语言编程实现，体元法计算示意图见图4。

图4 体元法原理Fig. 4 The principle of voxel method

树冠体积计算时，在每一横截面上逐个体元判断是否含有点云，含有点云的体元为有效体元，记为1，相反，不含点云的像元记为0，统计每一层有效像元个数T，则树冠体积计算公式为：

(1)

式中：V为树冠体积，m3；k为体元边长，m；n为树冠层数；Ti为第i层中的有效体元个数。

树冠表面积计算时，首先建立每层中各个体元间的拓扑关系，从头到尾遍历各个体元记录当前体元与其他体元的邻接个数，如果与4个体元邻接就说明有0条独立边，与3个体元邻接就说明有1条独立边，与2个体元相邻接则有2条独立边，与1个体元邻接则有3条独立边，最后统计所有体元的邻接个数得出每一层的独立边个数。设第i层独立边的个数为Ji， 统计所有层的独立边的个数，则树冠表面积计算公式如下：

(2)

式中：S为树冠表面积，m2；Ji为每一层的独立边个数。

1.3.3 数字高程模型法计算树冠体积和表面积

数字高程模型法计算树冠体积和表面积充分利用了点云数据所具有的高程信息，计算原理为：根据树冠点云数据的高程值，将具有相同高度的树冠表面的点用平滑的曲线连接，形成等高线，再根据等高线绘制方格网，其中角点处的体积为方格体积的1/4，边点体积为方格体积的2/4，拐点体积为方格体积的3/4，中心点体积为方格体积，所有点的体积之和为树冠体积。计算表面积时应选取树冠表面点，利用其高程值连接生成不规则三角网，分别计算每个三角形的面积，所有三角形面积之和即为树冠表面积。

数字高程建模工具选择的是基于CAD成图软件二次开发的CASS软件(版本号：9.0；公司：广东南方数码科技股份有限公司；产地：中国广州)，具体计算流程为：①树冠体积计算。首先将树冠点云数据转换为数字化测绘数据采集系统可以识别的.dxf格式，打开点云数据并提取高程保存为dat格式的高程数据。在软件中展开高程数据建立数字高程模型如图4所示，立体三角网，用闭合复合线圈出要计算树冠体积的区域，利用CASS软件的DTM法土方计算功能计算出点云体积。②树冠表面积计算。首先利用体元法选择具有1,2,3条独立边的体元，将具有独立边的体元内的点云作为树冠表面点云。再根据体积计算时高程数据提取的方法提取高程数据，建立三角网，选取表面积计算区域，利用CASS软件表面积计算功能，根据图上高程点来计算树冠表面积。

1.3.4 几何法计算树冠体积和表面积

由于树冠体积和表面积的真实值无法准确测量，所以在传统的树冠体积和表面积的计算中，根据树冠的冠型将其模拟成规则的几何体，以树冠的冠幅和冠高为参数，计算几何体的体积和表面积作为树冠的体积和表面积。本研究中根据实验树种的冠型将其分别近似为椭圆形、半球形和圆锥形，每种冠型的体积和表面积计算公式见表1。

表1 几何法树冠体积和表面积计算公式Table1 Geometrical formulas for calculating crown volumes and surface areas

2 结果与分析

2.1 树冠体积及表面积计算结果

对倾斜摄影测量得到的点云数据预处理后得到了50棵单木树冠的点云数据，共6个树种。分别使用体元法、数字高程模型法和传统几何法计算树冠体积和表面积。由于树冠形态的不规则性以及实际操作的困难性，在不损伤树木的情况下树冠体积和表面积的真实值是无法测量的，所以不对算法的计算精度进行比较。对比了3种方法的计算结果，从不同树种间的计算结果来看，美桐的3种方法计算结果相差最大，侧柏最小(图5)。从不同树种的冠型分析，侧柏的冠型更接近模拟的圆锥形，所以传统方法与体元法和数字高程法的计算结果间的误差较小。而美桐的冠型规则性较差，通过与规则几何体对比，传统几何法只能将其近似模拟为圆锥形，与实际冠型间仍有较大差距，所以计算结果误差较大。从树冠体积计算结果来看，传统几何法最大，数字高程法次之，体元法最小。从3种方法的原理分析，传统几何法没有考虑树冠表面不规则性和树冠内部的空隙，所以计算结果较大；而数字高程法仅考虑了树冠表面的不规则性，但没有考虑树冠内部的空隙，所以其计算结果小于传统几何法大于体元法。树冠表面积的计算结果中，体元法和传统几何法较为接近，这是因为这两种方法将树冠表面模拟得较为规则，而数字高程法则根据树冠表面真实形状进行计算。

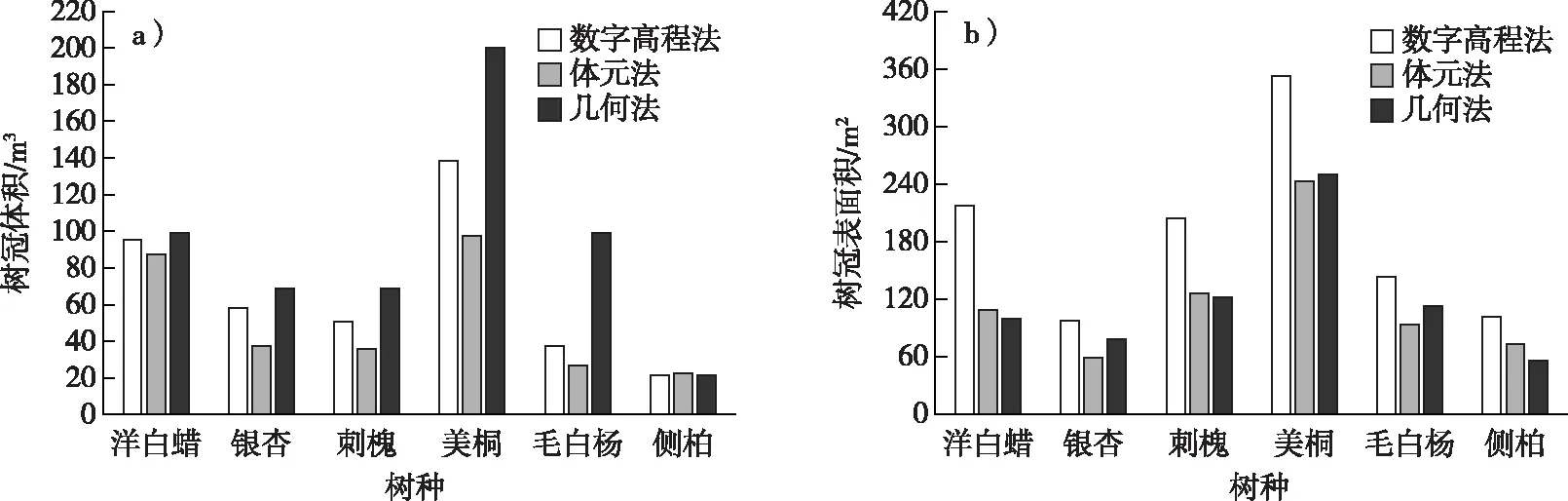
图5 树冠体积和表面积计算结果Fig. 5 Comparisons of tree crown volume and surface area calculation results

通过分析可知传统几何法的计算结果误差较大，所以本研究只分析体元法和数字高程法两种算法的差异及影响因素。使用两种算法计算结果间的相对误差和绝对误差来定量表示它们间的差异，具体计算公式为：

(3)

Eb=|r1-r2|

(4)

式中：Er为相对误差；Eb为绝对误差；r1为数字高程法计算结果；r2为体元法计算结果。

树冠体积和表面积计算结果见表2。由表2可知，除侧柏的树冠体积外，体元法计算的树冠体积和表面积均小于数字高程法的计算结果，两种算法计算的树冠体积相对误差最大为银杏的42.87%，最小为侧柏的5.60%；绝对误差最大为美桐的40.76 m3，最小为侧柏的1.23 m3。树冠表面积相对误差最大为洋白蜡的66.22%，最小为侧柏的33.47%；绝对误差最大为美桐的109.98 m2，最小为侧柏的29.38 m2。表2计算结果表明，银杏等树种的树冠内部空隙较多，侧柏的内部空隙较少，所以两种算法在树冠体积的计算上银杏的相对误差最大，侧柏的相对误差最小，而由于树冠表面不规则性的存在，导致两种算法间的相对误差均在30%以上。

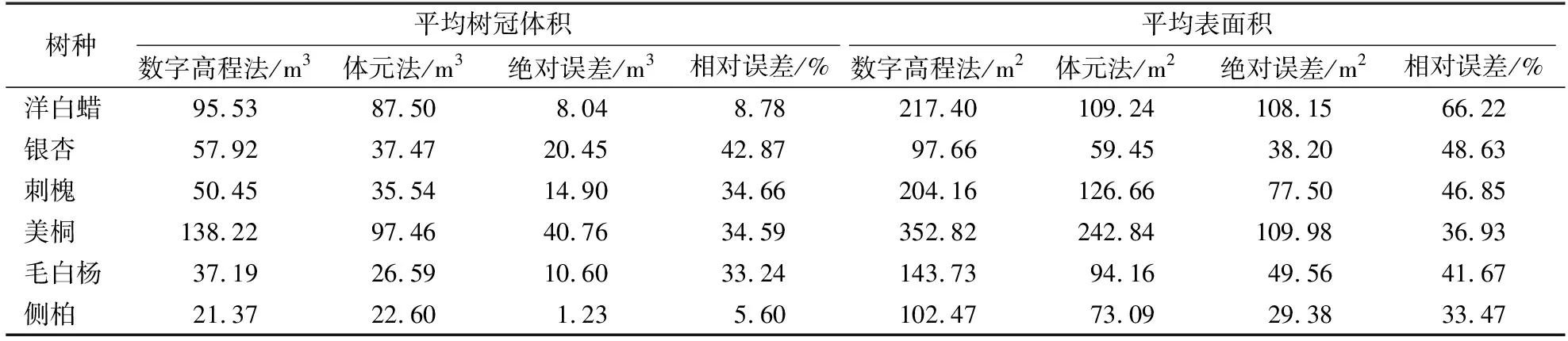
表2 树冠体积和表面积计算结果Table 2 Calculation results of canopy volumes and surface areas

2.2 树冠内部空间对两种算法的影响

树冠的内部结构主要体现在树冠的点云密度，点云密度的大小主要由单位体积的点云数量来体现，为便于分析对其进行均值标准化，计算方法如下：

(5)

(6)

式中：i为树冠编号，取值为1，2，…，n；n为树冠个数，本研究取50；Pi为点云密度；Pm为标准化后的点云密度；N为点云点数；V1为数字高程法计算的体积，m3；V2为体元法计算的体积，m3。

计算各树冠的点云密度，分别对点云密度与两种算法计算的树冠体积和表面积的相对差值进行拟合(图6)。从图6可以看出，点云密度与两种树冠体积算法的差值之间具有较好的相关性，决定系数为0.443 1，呈指数负相关关系，即点云密度越大，两种树冠体积算法的计算结果越接近。由两种树冠体积的计算原理可知，体元法计算树冠体积时充分考虑了树冠的内部空隙，而数字高程模型法在计算时只考虑了树冠的外部形态，忽略了树冠的内部结构，所以当树冠的点云密度越大时，树冠内部的空隙越小，树冠越接近一个实体，两种算法的计算结果差别也就越小。然而点云密度与两种表面积算法之间的决定系数为0.039 2，两者之间基本没有相关性，这主要是由于两种表面积算法在计算时都只考虑了树冠的表面点云，与点云密度不相关，只与树冠的外形及树冠表面特征点的选取有关。

图6 点云密度对不同算法间相对误差的影响Fig. 6 Influence of branch and leaf density on relative errors between different algorithms

2.3 冠型对两种算法的影响

同一树种的树冠形态大致相同，通过观察将实验地的6种树木依据其外形划分为6种不同冠型，不同树种间相对误差的统计结果见表3。由统计结果可知，两种算法在计算不同树种间结果的相对误差不同，并且体积计算时不同树种间的差异大于表面积。在树冠体积的计算中，不同树种间相对误差平均值最小的是窄圆锥形的侧柏树冠，为14.95%；最大的是椭圆形的银杏树冠，为56.55%。在树冠表面积的计算中，不同树种间相对误差平均值最小的也是窄圆锥形的侧柏树冠，为34.92%；最大是椭圆形的洋白蜡树冠，为55.69%。

两种树冠体积算法在同一树种间相对误差最大的为椭圆形的银杏树冠，差异最小的为宽圆锥形的美桐树冠；两种树冠表面积算法在同一树种间相对误差差异较大的为圆锥形的毛白杨树冠，差异较小的为宽圆锥形的美桐树冠。由于树冠的冠型并不是规则的几何体，在不同高度处的冠幅长短不一，为研究树冠表面规则性对两种树冠体积和表面积算法的影响，本研究以0.5 m为间隔在垂直方向上将树冠分层，计算每一层平均冠幅之间的标准差作为树冠的形状参数(K)，定量表示树冠表面的规则性，具体计算方法如下：

表3 不同树种计算结果相对误差Table 3 Statistical table of relative errors of calculation results of different tree species

(7)

式中：K为树冠的形状参数，m；n为树冠的层数；Ci为i层树冠的平均冠幅，m；Ca为树冠各层平均冠幅的均值，m。

分析树冠表面的规则性与两种体积和表面积计算结果间的关系，分别将冠型参数与两种树冠体积和表面积算法计算结果间的相对差值进行拟合(图7)。从图7可以看出，树冠表面的规则性对树冠体积和表面积的计算都有影响，两者都呈正相关，且与体积相对差值间的决定系数为0.349 6，与表面积相对差值间的决定系数为0.100 1，树冠表面的规则性对树冠体积计算的影响大于对树冠表面积计算的影响。在树冠体积和表面积计算时，体元法将树冠划分为一个个的体元，虽能反映树冠表面结构，但树冠表面越不规则其计算精度越差，而数字高程法能很好地反映树冠表面的规则性，计算结果受树冠表面影响较小。

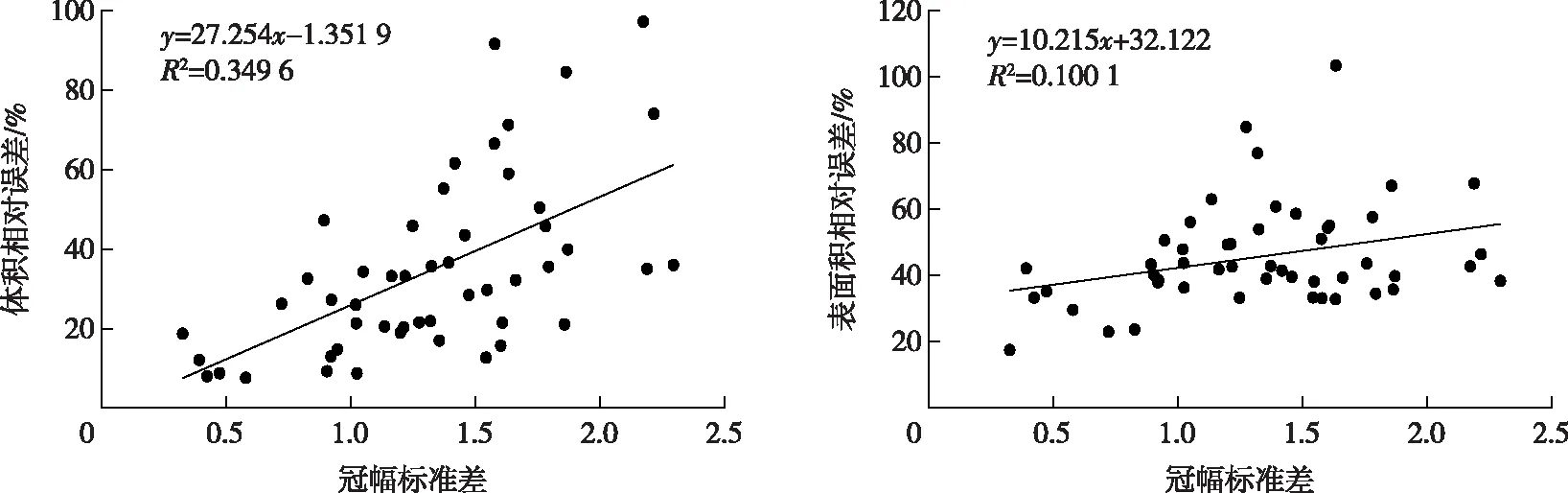
图7 树冠形状参数对不同算法间相对误差的影响Fig. 7 The influence of crown shape parameters on the relative errors between different algorithms

3 结论与讨论

本研究利用倾斜摄影测量得到的树冠点云数据对两种计算树冠体积和表面积的算法进行了对比分析，根据计算结果及两种算法的原理分析了两种算法在计算结果上产生差异的原因，结果表明：

1)数字高程法计算的树冠体积和表面积明显大于体元法的计算结果。树冠内部空隙是影响树冠体积计算结果的重要因素，洋白蜡和侧柏等树冠内部空隙小的树种计算结果较为接近，内部空隙大的银杏树种的计算相对误差高达42.87%，而树冠表面的不规则性导致两种算法在树冠表面积的计算中相对误差均在30%以上。

2)点云密度对两种树冠表面积算法的结果影响较小，对树冠体积算法的结果影响较大。树冠点云密度与两种树冠体积计算结果相对差值间的相关系数为0.443 1，点云密度越大，树冠内部空隙越小，数字高程法计算的结果越接近体元法，两者间相对差值越小。

3)两种算法在不同树种间计算结果差异较大。在计算侧柏树冠时，两种体积和表面积算法间的差异均小于其他树种，而在树冠体积计算时银杏树冠的差异最大，在树冠表面积计算时洋白蜡最大。

4)树冠表面的规则性与两种体积和表面积计算结果均具有相关性。冠型参数与体积相对差值间的决定系数为0.349 6，但与表面积相对差值间的相关性较差，决定系数为0.100 1。冠型参数越大，树冠表面越不规则，体元法不能很好地反映冠型变化，两种算法间的差值变大。

本研究分别从树种冠型、树冠表面规则性和点云密度等方面对两种算法进行了对比分析，为实际树冠体积和表面积的计算提供理论支持。虽然从两种算法的理论上来说，体元法能够更真实反映精度，但是计算过程较慢，另外需要自行二次开发计算工具，相对麻烦，而利用数字高程法，可以依赖现有的软件提供的体积表面积计算工具，快速得到树冠结构因子。所以，对于树木内部空间较小、冠型较规则的树木(例如侧柏)，或对于不考虑树木内部结构的研究(例如三维绿量等)，数字高程法仍有较好的应用前景。如果要求计算结果准确，或树冠内部空隙较多，则体元法较为适合。

另外本研究只选择了北京地区6个常见树种夏季的测量数据，并没有本地区所有树种以及同一树种其他季节的数据，在算法中只选择了两种算法来对比分析。在今后的研究中将进一步增加实验数据，并且进一步提高算法的速度和精度。