基于分段摩阻因数的水平井延伸极限分析及应用
覃 岚, 董国昌, 郭建勋, 李 玮, 李卓伦, 陈 卓
( 1. 东北石油大学 石油工程学院,黑龙江 大庆 163318; 2. 中国石油吉林油田分公司 钻井工艺研究院,吉林 松原 138000 )
0 引言
在水平井钻井延伸长度不断增长的趋势下,人们开展井眼延伸极限预测研究。以长宁页岩气实钻数据为基础,刘茂森等[1]分析钻机承载能力、钻柱安全系数等因素对水平井延伸能力的影响,并推导相应计算模型;根据整体钻柱摩阻力分析的间隙元理论,闫铁等[2]建立大位移井延伸极限的力学判断准则和计算模型,分析并确定影响大位移井极限延伸能力的主要因素;MEERTENS R等[3]考虑评价开发概念的选择、井身结构设计和钻井风险等,对大位移水平井进行实例分析,探讨井眼极限延伸能力;MASON C J等[4]通过统计资料分析研究水平井延伸极限,探讨浅井、中层井及深井延伸极限的影响因素。
摩阻扭矩是水平井极限延伸能力的主要制约因素,摩阻因数预测的准确性是影响摩阻扭矩计算的主要影响因素[5]。摩阻因数确定方法多是通过钻井实测数据反演计算得到,根据钩载、扭矩等参数与钻柱摩阻扭矩模型计算结果进行拟合,并考虑一定精度得到摩阻因数[6-7]。基于钻柱摩阻扭矩模型,JOHANSICK C A等[8]考虑泥浆性能与井眼的影响,提出摩阻因数计算公式;张建群等[9]考虑钻柱拉力增量的影响,修正摩擦阻力模型,计算大庆油田中区定向井的摩阻因数;代奎等[10]编制摩阻因数计算软件,结合水平井钻井实测数据,确定不同摩阻性能井段的摩阻因数;基于钻柱力学模型,宋巍等[11]应用近钻头多参数测量仪实测数据,预测套管段和裸眼段摩阻因数。
在传统摩阻因数反演计算中,先将井眼分为套管段和裸眼段,再分别计算两段的平均摩阻因数。水平井的井眼约束复杂,摩阻因数的取值受井眼轨迹、地层性质、套管井段、裸眼井段、钻具组合及井眼清洁等因素的影响,传统反演方法通过套管段和裸眼段摩阻因数难以准确描述水平井摩阻因数[12-16],影响水平井摩阻扭矩及延伸极限的预测精度。在传统反演方法的基础上,提出一种水平井分段摩阻因数反演预测方法。利用系统聚类分析,划分不同摩阻因数的井段,利用模拟退火算法反演计算各个井段摩阻因数的最优值,建立水平井延伸极限的判断准则和预测模型,对水平井邻井的延伸极限进行现场预测分析。
1 分段摩阻因数反演模型
1.1 计算方法
1.1.1 系统聚类算法
系统聚类分析首先将研究的对象各自看成一类,计算分析两两之间的亲疏关系,合并亲疏程度最高的两类成为一个新类,再重新计算新类与其他类之间的亲疏关系,通过不断计算合并直至所有类合成一类[17];结合肘部法则,画出聚类系数图,估算最优聚类数量。
采用欧氏距离计算法分析各对象间的亲疏关系:
(1)
式中:d(xi,xj)为研究对象xi与xj之间的距离;xie、xje(e=1,2,…,E)分别为研究对象xi、xj的第e类影响因素指标。
令dij=d(xi,xj),D=(dij)n×p,可得出距离矩阵:
(2)
式中:n为研究对象总数;dij=dji。
聚类系数J为
(3)
式中:Cl(l=1,2,…,L)为第l类研究对象;ul为第l类研究对象的重心位置。
1.1.2 模拟退火算法
模拟退火算法[18]模拟固体的物理退火过程,将目标函数的解空间对应状态空间,再按照状态产生函数随机的解;根据接受概率选择是否接受当前解为新解,逐步寻优[19]。
接受概率P根据Metropolis准则求取,系统从状态1变为状态2时,摩阻因数μ变为μ′,相应的能量从f(μ)变为f(μ′),其概率为
(4)
式中:Tt为退火过程中t时刻的温度。
如果f(μ′)≤f(μ),系统接受状态1,令μ=μ′,f(μ)=f(μ′);否则,以一个随机的概率接受或丢弃状态1。状态2被接受的概率为
(5)
1.2 摩阻扭矩
摩阻扭矩计算模型主要有软杆模型和刚杆模型。软杆模型忽略钻柱刚度的影响,运算过程简单,计算方法可靠,适用于直井和井斜角较小且变化平缓的井型,但在井眼曲率变化较大或钻柱刚度较大的井段,易产生明显误差;刚杆模型计算过程较复杂,由于考虑钻柱刚度较大,更适用于井眼曲率较大的定向井、水平井等非直井井型,但在曲率较小、刚度较小的平滑井眼中,易出现计算结果收敛困难、解稳定性较差的情况[20-23]。
水平井井眼曲率在直井段和稳斜段变化小,忽略钻柱刚度的影响,可采用软杆模型;在造斜段井眼曲率较大,采用刚杆模型;在加重钻杆至钻头井段,由于加重钻杆和底部钻具组合的刚度较大,采用刚杆模型[24-25]。水平井摩阻扭矩力学模型见图1。
软杆模型假设钻柱是一条不承受弯矩、可承受扭矩的软杆,井眼曲率为常数,忽略井下钻柱的动力效应,钻柱轴线与井眼轴线一致[26]。在理想的井眼轨迹曲线上,任一弧长为dl的微元段的钻柱单元受力分析见图2,其中N为钻柱与井壁的接触正压力;We为钻柱在钻井液中的重力;T为轴向力;Mt为扭矩;Fμ为摩阻力;α、φ分别为井斜角和方位角。
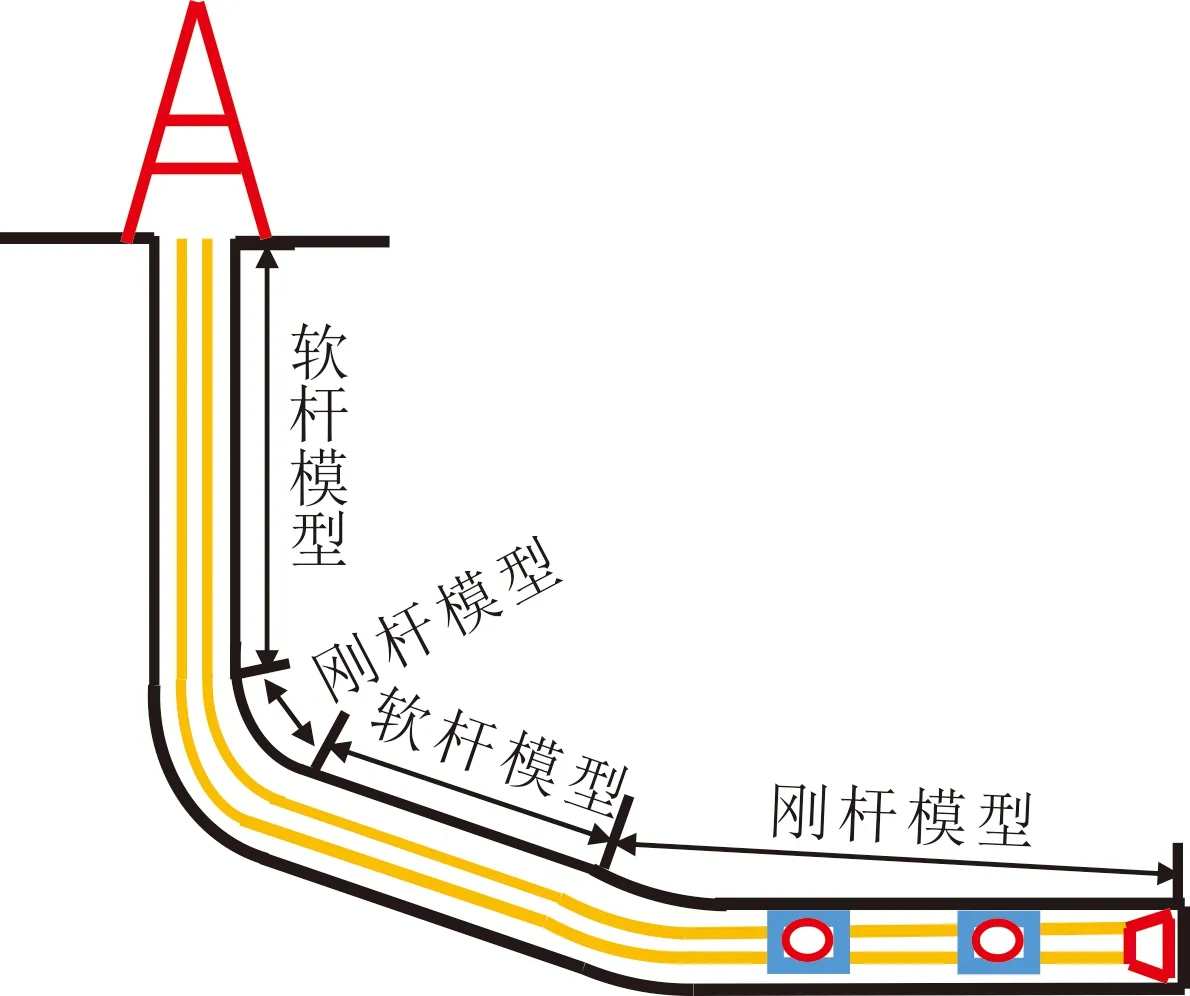
图1 水平井摩阻扭矩力学模型Fig.1 Mechanical model of friction torque in horizontal well
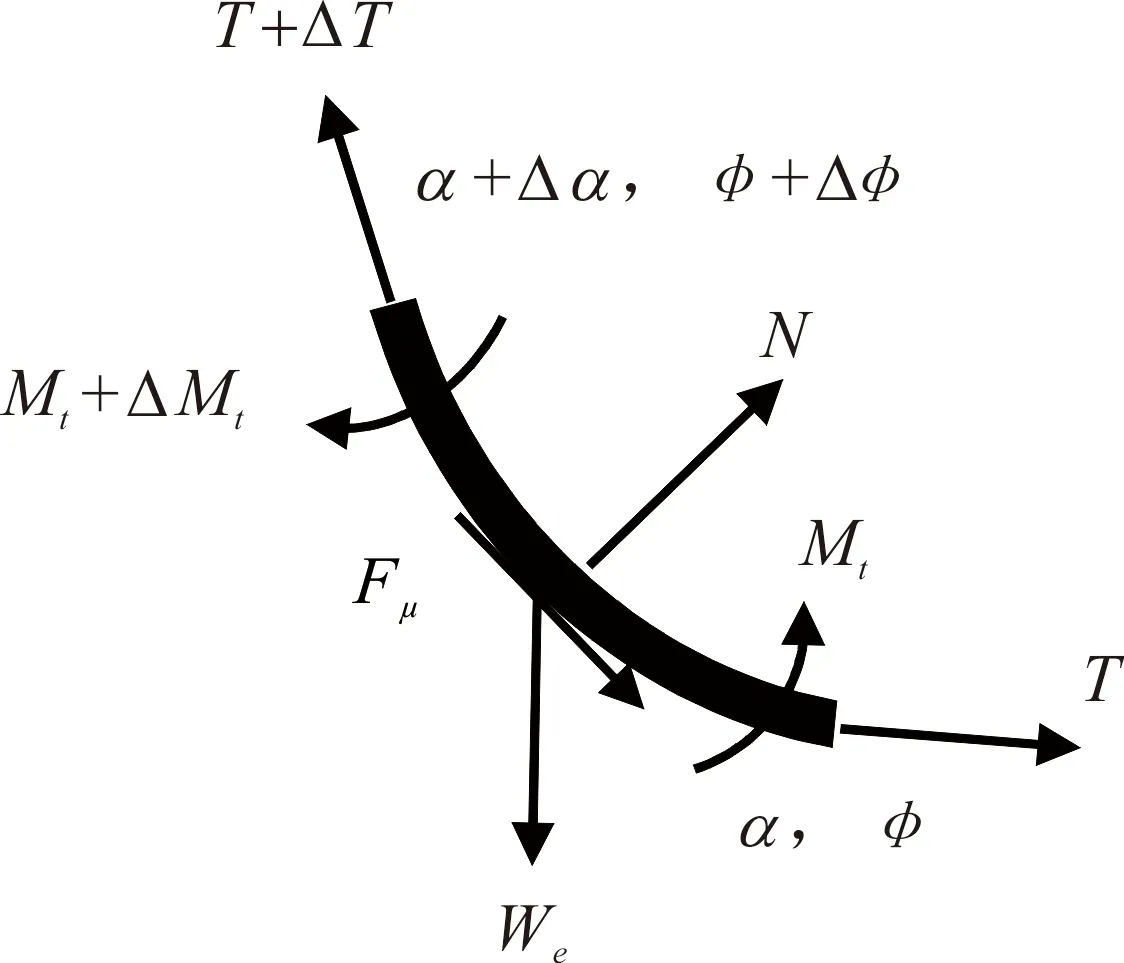
图2 软杆模型钻柱单元受力分析Fig.2 Stress analysis of drill string unit of soft rod model
(6)
式中:μa为轴向摩阻因数;μt为周向摩阻因数;r为钻柱单元半径。
刚杆模型假设钻柱与井壁连续接触,轴线与井眼曲线一致,井壁为刚性,钻柱单元体所受重力、正压力、摩阻力均匀分布[27]。在井眼轴线坐标系上任取一弧长为ds的微元体AB,进行受力分析。以A点为始点,轴线坐标为s,B点为终点,轴线坐标为s+ds。刚杆模型钻柱单元受力分析见图3,其中Mb为钻柱微元段上的弯矩;Fn、Fb分别为n方向、b方向上的剪力。
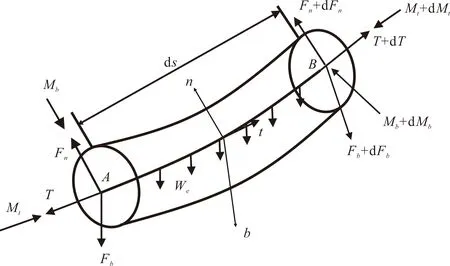
图3 刚杆模型钻柱单元受力分析Fig.3 Force analysis diagram of drill string unit of rigid rod model
(7)
式中:K为井眼曲率;Kα为井斜变化率;Kφ为方位变化率;Nn、Nb分别为n方向、b方向上的均布接触力。
釆用速度分解法计算摩阻因数,按轴向和周向速度的比例对摩阻因数进行分解:
(8)
式中:va为钻柱轴向运动速度;vt为钻柱周向运动速度。
1.3 目标函数
运用模拟退火算法进行分段摩阻因数反演预测最优值时,水平井各井段的摩阻因数μi(i=1,2,…,n)为优化变量。水平井施工过程中,可以得到不同井深下各个井段的大钩载荷实测值Hi(i=1,2,…,n)和井口扭矩实测值Mi(i=1,2,…,n);应用水平井摩阻扭矩模型,代入摩阻因数、钻压、井斜角、方位角等参数,从钻头处逐段计算钻柱上端(靠近地面)的轴向力、扭矩,可得大钩载荷计算值Hcal和井口扭矩计算值Mcal。
将各个井段的大钩载荷、井口扭矩计算值与实测值之间的误差,作为优化问题的目标函数:
(9)
(10)
计算大钩载荷和井口扭矩的平均误差绝对值δMAPE1、δMAPE1,判断预测模型的准确性:
(11)
(12)
1.4 反演流程
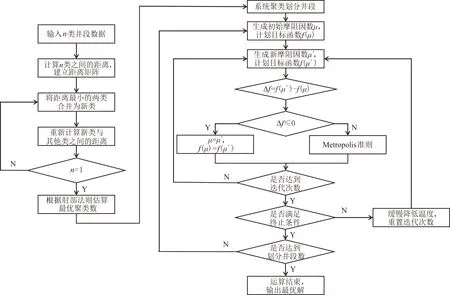
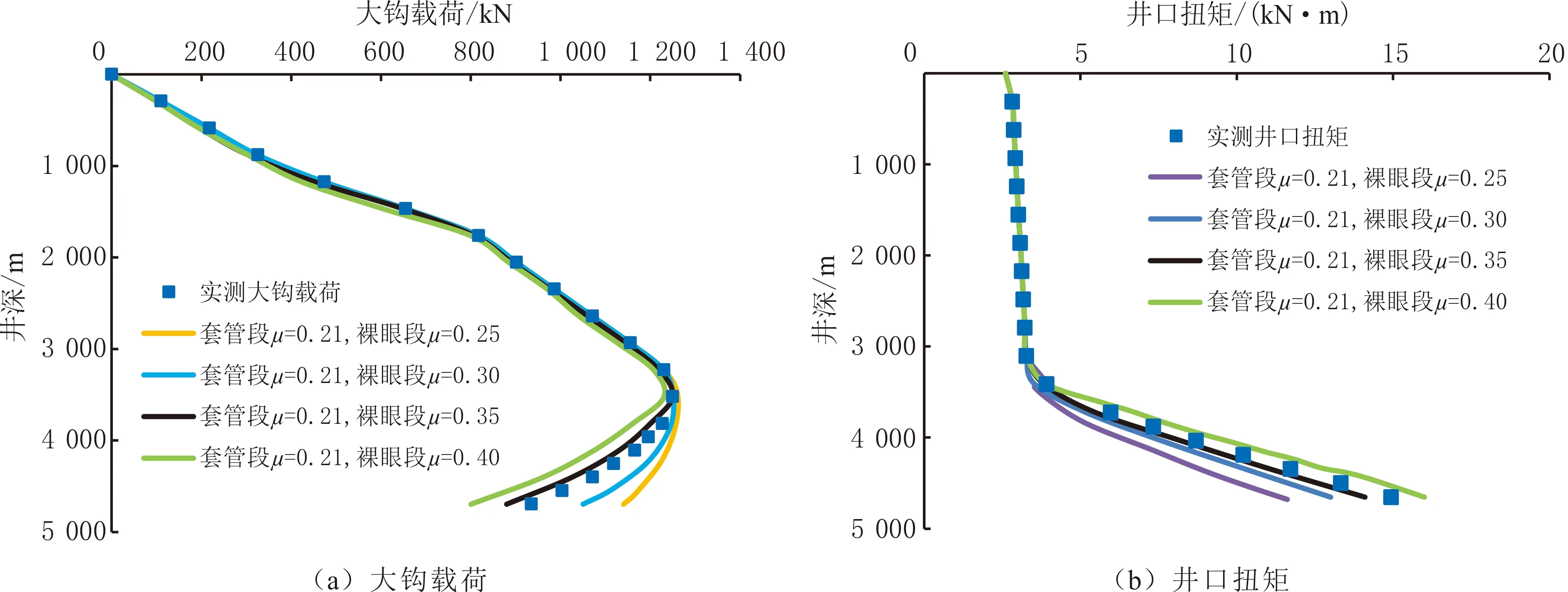
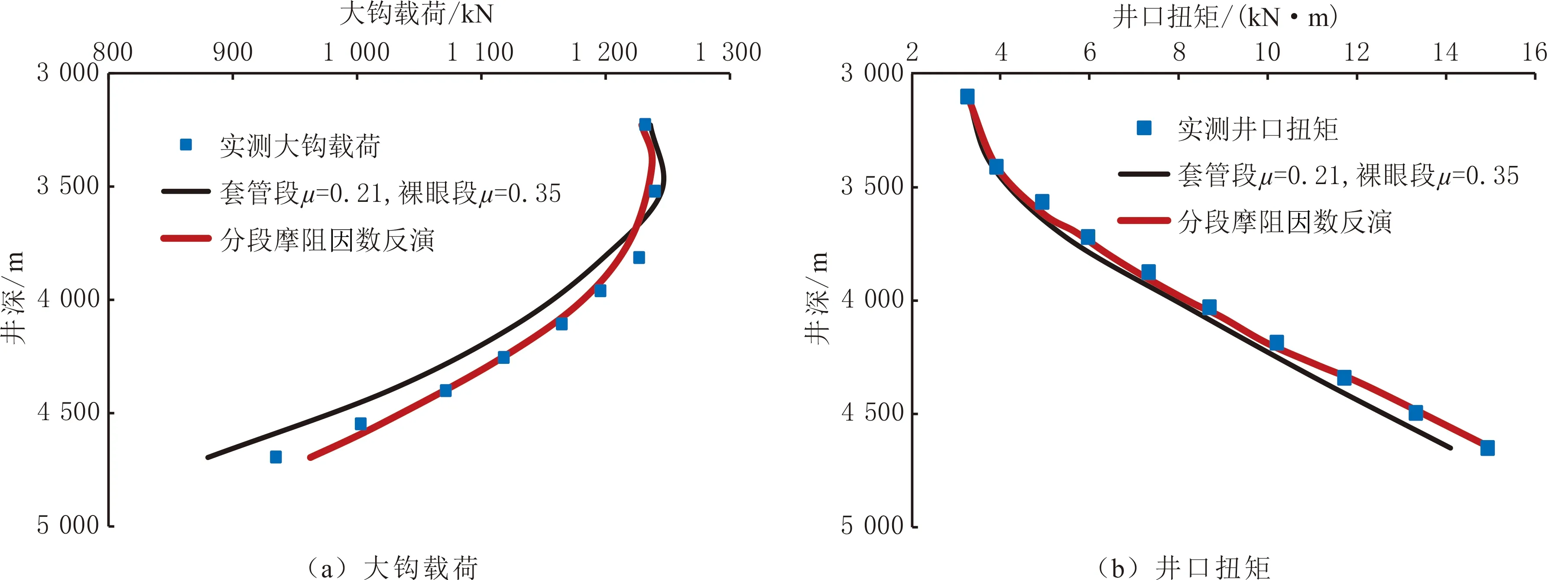
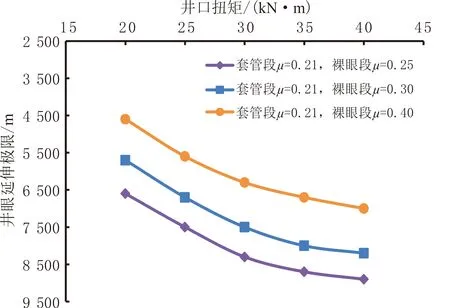
分段摩阻因数反演流程见图4。完成井眼分段,根据工程经验生成初始摩阻因数μ;结合水平井摩阻扭矩模型及实测大钩载荷、井口扭矩,计算摩阻因数μ对应的目标函数值f(μ)。在μ附近随机生成另一个摩阻因数μ′,计算μ′对应的目标函数值f(μ′):如果f(μ′)≤f(μ),将μ′赋值给μ,f(μ)=f(μ′),判断是否达到迭代次数,若未达到,则重复上面的步骤;如果f(μ′)>f(μ),依据Metropolis准则,计算接受μ′的概率P,然后生成一个[0,1]之间的随机数r,如果r 2.1 判断准则 水平井延伸极限是指在一定制约条件影响下,钻井施工能达到的极限长度。在地质条件具备的基础上,水平井延伸极限受钻机承载能力、井身剖面、井眼几何特性、井眼清洁、钻井液性能、井壁稳定、岩石可钻性、钻柱强度等因素的共同影响[28-29]。为确保井眼顺利延伸,至少需要满足条件: (1)钻机承载能力。钻机各部分的额定工作载荷主要包括钻机的提升能力和扭矩输出能力。为了确保水平井水平段的顺利钻进,在各种工况下大钩载荷、井口扭矩必须在钻机的额定载荷范围内。 (2)岩石破碎条件。钻头破碎岩石时,加载在钻头上的载荷必须大于门限载荷,否则钻头无法破碎岩石继续钻进,不能达到钻井的延伸极限。 (3)摩阻力条件。正常钻进施工过程中,必须保证钻柱在井眼中运动方向上的动力大于钻柱所受摩阻力的总和。 图4 分段摩阻因数反演流程Fig.4 Segmented friction factor inversion process (4)钻柱强度条件。为确保钻柱在工作过程中不发生断裂破坏,需要校核各工况下钻柱任一截面所受应力,使之小于材料自身的许用应力。 (5)钻柱刚度条件。钻井施工中,为确保钻柱正常工作,钻柱的弯曲变形必须小于钻柱的许用变形值。 2.2 预测模型 应用水平井钻柱摩阻扭矩模型,计算井下钻柱延伸长度L,轴向载荷与门限钻压的差值等于长度为L的钻柱产生的摩阻力: (13) 式中:Fm为所钻地层岩石的门限钻压。 水平井延伸极限预测流程为:首先调研应用区块现场钻井数据,确定钻机的最大负荷,再对计算井的整体钻柱进行力学分析,应用延伸极限判定准则判定钻柱是否能够继续钻进延伸。若满足判定准则,根据式(13)将井眼轨迹向前延伸L,然后重新进行水平井钻柱力学分析,判断是否可以继续延伸;若不满足判定准则,则将延伸长度L减半,返回水平井钻柱力学分析,判断是否可以继续延伸。直到L=0 m时,计算结束,将延伸长度迭加求和,可估算延伸极限Lz。 将水平井分段摩阻因数反演方法应用于吉林油田一口完钻水平井。该井完钻井深为4 713.00 m,垂深为3 355.00 m,造斜点深度为3 008.00 m,水平位移为1 538.63 m。采用三开井身结构:一开采用直径为 444.5 mm的钻头钻至202.00 m井深,下入直径为 339.7 mm的表层套管固井;二开采用直径为311.1 mm钻头钻至1 592.00 m井深,下入直径为224.5 mm的技术套管固井;三开采用直径为215.9 mm钻头钻至4 713.00 m井深,下入直径为139.7 mm的油层套管固井。水平段钻具组合:直径为215.9 mm钻头+近钻头地质导向+直径为165.0 mm无磁钻铤×1根+止回阀+直径为127.0 mm钻杆×170根+直径为127.0 mm加重钻杆×60根+投入式止回阀+直径为127.0 mm钻杆。 按照不同井深的地层岩性、井斜、钻井液性能等,划分不同摩阻因数的井段。钻柱摩阻因数的影响因素较多,选取10种因素的数据作为基础指标:井深(X1)、井斜角(X2)、方位角(X3)、垂深(X4)、狗腿度(X5)、岩性(X6)、井眼套管封隔(X7)、钻井液密度(X8)、钻井液黏度(X9)、排量(X10),根据要素指标进行井段分类。影响因素指标统计结果见表1。 表1 某完钻水平井影响因素指标统计结果 对提取的各影响因素指标进行转换及标准化处理并开展聚类分析,再根据肘部法则得到聚类系数折线图(见图5),估算最优聚类数量。由图5可以看出,类别数l从1到10,聚合系数变化大,在类别数达到10时,折线的下降趋势变缓,聚合系数的变化幅度明显减小。聚类的类别数设定为10,各井段划分方案见表2。 图5 某完钻水平井聚类系数折线图Fig.5 Clustering coefficient line graph of a drilled horizontal well 根据工程经验,缩小摩阻因数取值范围。套管段摩阻因数取0.25,裸眼段摩阻因数取0.30。在第1段套管内摩阻因数取值为0.15~0.35,第2~4段为裸眼直井段,摩阻因数取值为0.20~0.40,对于造斜段和水平段考虑井眼曲折度、井眼清洁等,第5~7段摩阻因数取值为0.30~0.45,第8~10段摩阻因数取值范围设置为0.30~0.50。 结合三开实测大钩载荷和井口扭矩,运用分段摩阻因数预测方法进行反演分析,确定第1段摩阻因数后,进行下一段摩阻因数反演,得到分段摩阻因数反演结果(见表2)。 表2 某完钻水平井井段划分及分段摩阻因数反演结果 采用传统摩阻因数反演计算方法,将井眼分为套管段及裸眼段,再结合水平井钻柱摩阻扭矩模型及现场实测数据,进行摩阻因数反演,传统方法预测与实测大钩载荷、井口扭矩对比见图6。由图6可知,传统方法预测裸眼段的摩阻因数为0.35时,大钩载荷和井口扭矩最接近实测数据。 图6 某完钻水平井传统方法预测与实测大钩载荷、井口扭矩结果Fig.6 Comparison of measured hook load and wellhead torque with predicted value by traditional method of a drilled horizontal well 在造斜至井底段(3 008.00~4 713.00 m),采用裸眼段摩阻因数为0.35的传统方法和水平井分段摩阻因数反演预测方法计算大钩载荷和井口扭矩,并与现场实测数据结果对比(见图7)。由图7可知,分段摩阻因数反演计算的大钩载荷和井口扭矩与实测数据基本吻合,传统方法计算结果连续偏离实测数据。大钩载荷和井口扭矩的平均误差绝对值分别为3.72%、3.45%,较传统反演方法(8.23%、7.16%)预测精度分别提高54.8%、51.8%,能更准确预测沿水平井井眼的摩阻因素,有利于工程决策。 图7 某完钻水平井不同方法预测与实测大钩载荷、井口扭矩结果Fig.7 Comparison of measured hook load and wellhead torque with predicted values by different methods of a drilled horizontal well 应用式(13)计算得到不同摩阻因数的井眼延伸极限(见图8)。由图8可以看出,随摩阻因数的增加,同类型邻井延伸极限明显降低,基于分段摩阻因数方法计算的井眼延伸极限更可靠。 图8 某完钻水平井不同摩阻因数的井眼延伸极限Fig.8 Borehole extension limit under different friction factors of a drilled horizontal well (1)在传统摩阻因数反演方法基础上,运用系统聚类分析,结合水平井钻柱摩阻扭矩计算模型,提出水平井分段摩阻因数反演预测方法;基于分段摩阻因数,综合考虑钻机承载能力、岩石破碎条件、摩阻力条件、钻柱强度条件、钻柱刚度条件因素,建立水平井延伸极限的判断准则和预测模型。 (2)某完钻水平井分段摩阻因数反演预测结果与现场实测数据具有良好相关关系,大钩载荷和井口扭矩的平均误差绝对值分别为3.72%、3.45%,较传统反演方法预测精度分别提高54.8%、51.8%,能够得到更详细准确的摩阻因数。 (3)在相同的钻机性能下,井眼延伸极限随摩阻因数的增大而明显降低,基于分段摩阻因数计算的井眼延伸极限预测结果更可靠。2 水平井延伸极限预测
3 现场应用
3.1 划分井段
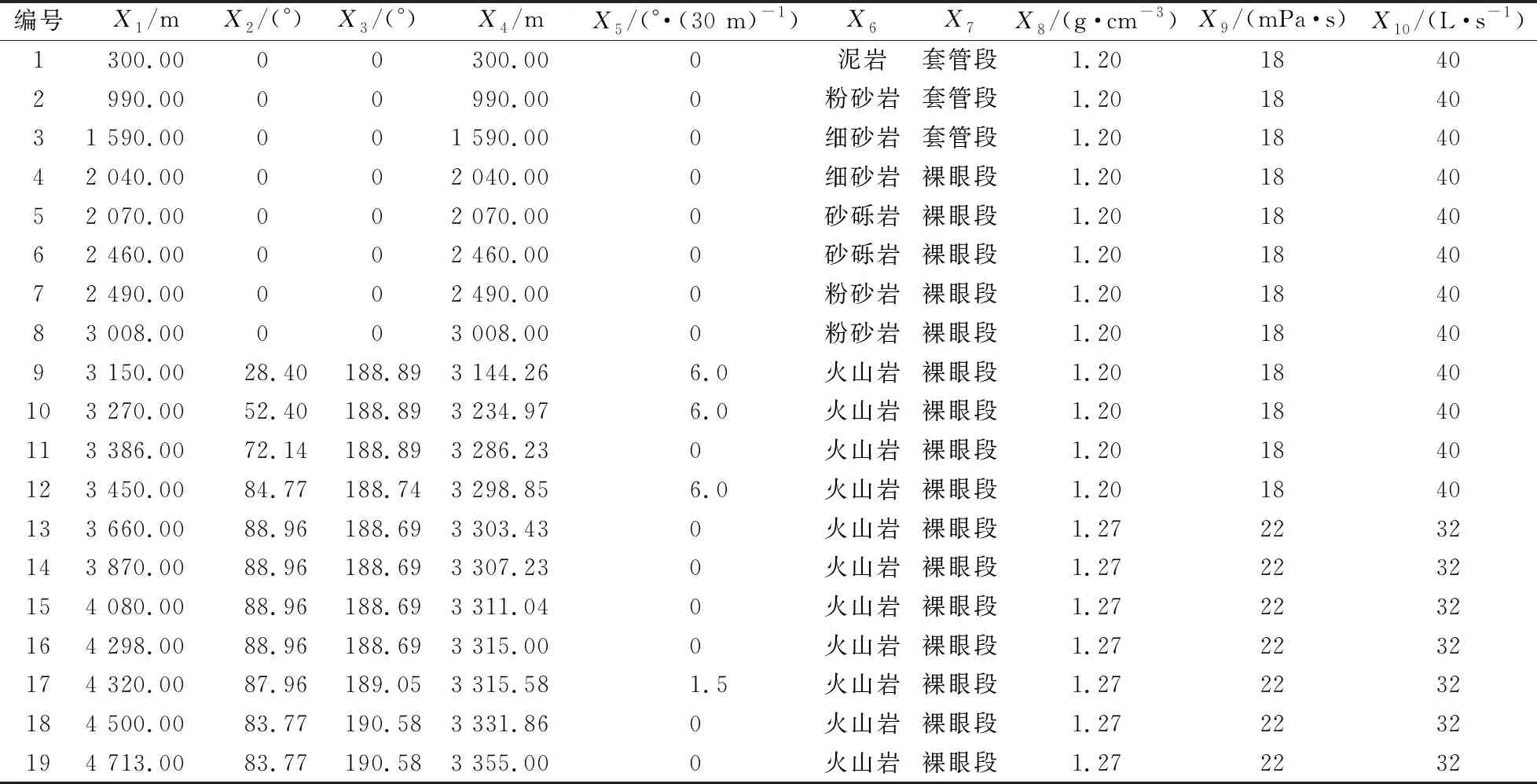
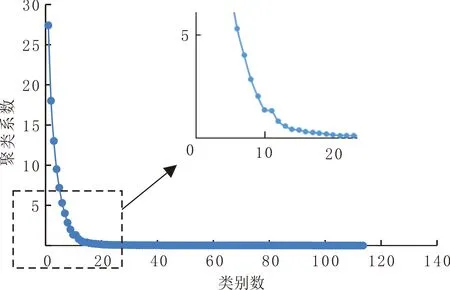
3.2 反演结果

4 结论

