樟树林林层划分及树高—胸径模型拟合

李爱国， 张扬扬， 林 强， 宋庆安

(1.汉寿县林业局， 湖南 汉寿 415900； 2.湖南省林业科学院， 湖南 长沙 410004)

林层是指森林垂直结构中乔木层林木树冠形成的树冠层次，一般也称为林相或林冠层。林层是森林调查中最为基本的调查因子之一，常用于描述林分的垂直结构[1]。林层通常被划分为单层林和复层林，单层林是指只有一个林层的林分，常见于同龄纯林，而复层林则拥有多层，常见于天然林[2]。森林的垂直结构是森林对环境的适应，是森林群落的基本特征，反映了群落树木间竞争、能量传递等重要生态过程[3]。林层的划分和存在自诞生后一直存在争议，例如根据树高、生活型、龄级、树冠高度等因素作为分层依据[4]。林层的划分方法众多，例如克拉夫特(Craft)树木分级法、判别分析法、林冠分层指数法[5]、Landscape Management System (LMS)分层算法[6]和TSTRAT法[7]等。其中TSTRAT方法除了较低林层边界的确定存在问题外，其他林层的划分效果很好，在实际应用中较为广泛[8-9]。树木的树高—胸径曲线是进行森林资源调查、调整林分结构等森林管理活动的基础[10]，在森林资源调查、碳汇储量计算、收获量估算等方面应用广泛[11]。目前广泛应用的胸径—树高模型包括线性回归模型、神经网络模型和混合效应模型等，已经较为成熟。

公益林是指以生态效益和社会效益为主体功能，旨在改善人类生存环境的森林，其主要作用包括维护生态平衡、保护生物多样性、森林游憩、国土防护等，保障了我国生态安全、人民群众生活、森林资源持续发展，是我国森林资源中最为重要的类型之一[12-13]。湖南省汉寿县森林资源较为有限，公益林面积不大，但承担了支撑地区生态和环境的重要任务。因此，根据国家对森林质量精准提升的要求，迫切需要开展森林质量提升的相关研究，确保森林质量精准提升的实施效果，从而为地区提供更加优质的生态服务。本文以汉寿县境内国家级公益林固定监测样地调查数据为基础，选取樟树样地为研究对象，分析了样地的林分结构，并以樟树为对象，通过建立拟合模型来描述树高—胸径关系，为分析地区林分结构、减轻外业调查和数据核查工作提供了帮助。

1 研究区概况

汉寿县属常德市，县域总面积2021km2，地域上东濒沅江市、南县，南界资阳市、桃江县，西接鼎城区，北抵西湖农场，与安乡市隔河相望。属雪峰山脉向洞庭湖平原过渡地带，南部丘陵属雪峰山余脉，全境地势由南向北呈阶递状下降，以平原为主，水系发达，平原占49.07%，丘陵岗地占22.44%，其余为水面占28.49%。县域内有河流30条，主要河流为沅水和澧水。主要湖泊有太白湖、围堤湖和目平湖。汉寿县林地面积为55113.33hm2，公益林面积10758.40hm2，森林空间保护率为19.52%。

2 数据来源与分析方法

2.1 数据来源

本次研究数据来源于湖南省公益林2019年面上固定样地数据，其中位于汉寿县的2个，固定样地的面积为25 m(垂直等高线)×40 m(平行等高线)，选取其中一个优势树种为樟树(Cinnamomumcamphora)的乔木样地，对样地进行每木检尺，获得每株树木的胸径、树高、冠幅和第一活枝高数据用于下一步分析。

2.2 数据分析方法

正态分布函数是拟合林分结构参数分布的常用函数，本研究选择正态分布函数对林分的结构参数分布进行拟合。偏度系数描述了随机变量分布的不对称程度。峰度系数反映了与正态分布相比，分布变量的尖锐度，因此我们分别计算了样本分布的偏度系数与峰度系数。

选取样地中所有的37株乔木的树高、冠幅和第一活枝高进行林层划分。林层划分采用TSTRAT分层算法[7]，其原理是利用光竞争区域、林冠长和枝下高确定一个林层高度临界值(HCV)，当林木的个体树高高于这一临界值时划为同一林层，直至将所有林木都划分到相应的林层中。计算方程为：

HCV=(1-竞争区域指数)×CL+HBLC

(1)

式中：HCV为林层高度临界值；CL为林冠的长度；HBLC为第一活枝高；竞争区域指数可通过修正其他研究者确定的竞争估计值和观察研究区域内林木树冠的关系来确定，本次竞争指数采用文献中常用的60%[9]。

提取25株樟树的胸径和树高数据，并选取广泛适用且具有生物学意义的一元线性模型、二项式模型等[14](见表1)进行树高—胸径模型构建。本研究使用剩余残差和以及剩余标准差(MSE，Mean Square Error)来进行模型的精度检验[15]。样地数据处理及模型构建用SPSS 21.0及Excel 2013完成。

表1 构建4种模型的公式Tab.1 Formulas for constructing four models模型公式一元线性E(H)=β0+β1D二项式E(H)=β0+β1D+β2D2对数函数E(H)=β0+β1ln(D)指数函数E(H)=β0×Dβ1 注: H表示树高,D表示胸径,β0、β1、β2表示待估参数。

3 结果与分析

3.1 樟树林的林层划分

汉寿县樟树林固定样地的胸径分布范围为8.00～25.90 cm，平均值为16.38 cm；树高分布范围为8.00～13.50 m，平均值为11.37 m；第一活枝高分布范围为0.20～7.00 m，平均值为3.27 m；冠幅分布范围为1.90～7.75 m，平均值为4.18 m；树冠长度分布范围为2.20～13.10 m，平均值为8.11 m(见表2)。根据计算结果，本次胸径和第一活枝高分布的偏度系数分别为-0.02和-0.06，表明分布较平坦，峰度系数分别为-0.71和-0.75，表明二者的分布呈左偏分布且离散程度较大；树高和树冠长度的偏度系数为-0.83和-0.13，峰度系数为-0.29和-0.61，其分布呈高度左偏且较为离散；冠幅的偏度系数和峰度系数为0.76和-0.19，分布呈高度右偏且较为离散。

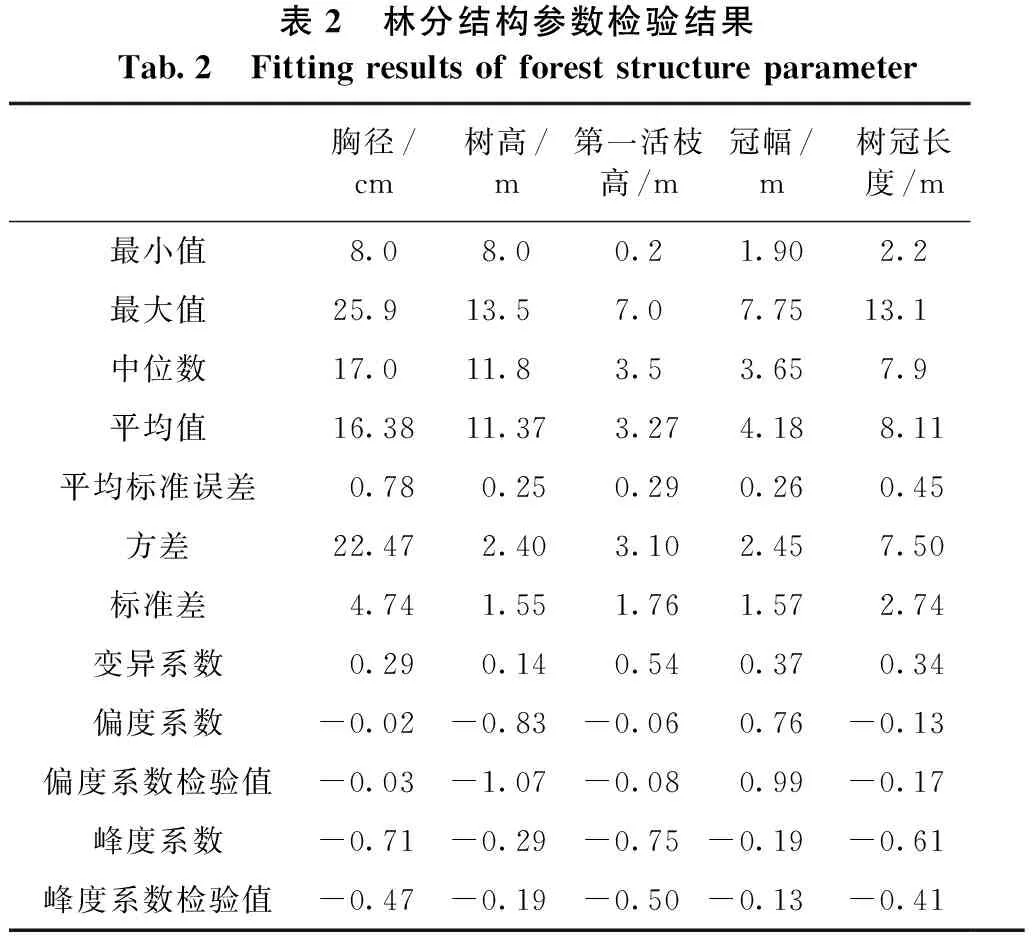
表2 林分结构参数检验结果Tab.2 Fitting results of forest structure parameter胸径/cm树高/m第一活枝高/m冠幅/m树冠长度/m最小值8.08.00.21.902.2最大值25.913.57.07.7513.1中位数17.011.83.53.657.9平均值16.3811.373.274.188.11平均标准误差0.780.250.290.260.45方差22.472.403.102.457.50标准差4.741.551.761.572.74变异系数0.290.140.540.370.34偏度系数-0.02-0.83-0.060.76-0.13偏度系数检验值-0.03-1.07-0.080.99-0.17峰度系数-0.71-0.29-0.75-0.19-0.61峰度系数检验值-0.47-0.19-0.50-0.13-0.41

通过TSTRAT分层算法计算林分分层结果(见图1)。从图中可知林层的HCV为5.64 m，第一林层高度为7.86 m，且本样地为单层林分，表明该样地的林层结构较为单一。总体而言，上述林分树木单株之间互相重叠，单株间竞争强度较高，林冠产生一定的分化，不利于大径阶个体的生长，亟需进行调整。

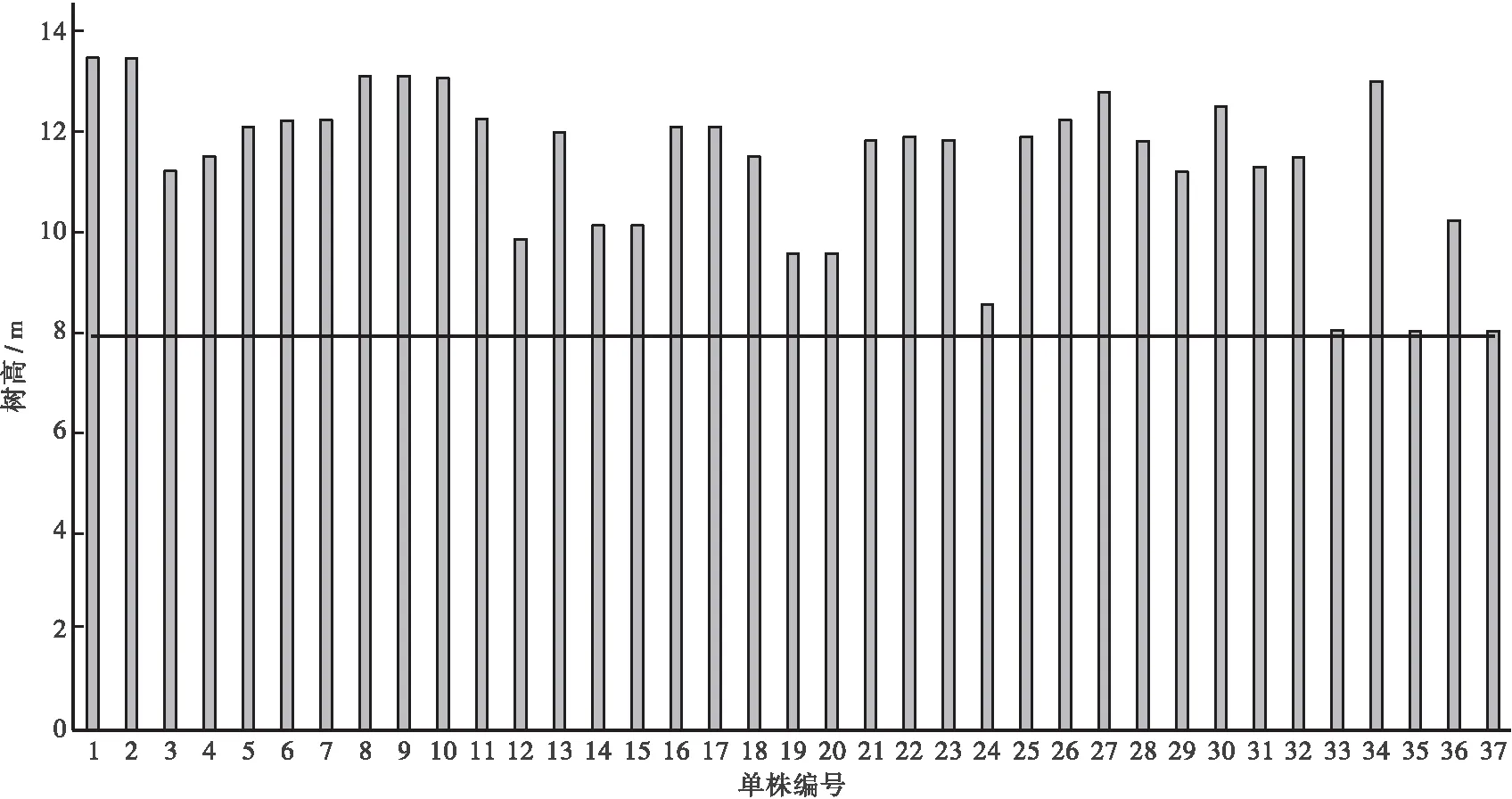
图1 樟树林的林层分布

3.2 樟树树高—胸径模型的拟合与评价

樟树树高—胸径模型的拟合结果见图2和表3。从图2和表3可知：4种模型中，残差和最大的为对数函数(43.24)，其次是指数函数(43.02)，最小的为一元线性模型(42.45)和二项式模型(42.39)，表明一元线性模型和二项式模型的拟合效果较好，对数和指数函数的拟合效果较差；从MSE分析的结果来看，MSE最大的为对数函数(1.729)，其次是指数函数(1.721)，最小的为二项式模型(1.696)和一元线性模型(1.698)，结果表明一元线性模型和二项式模型的拟合效果较好，对数和指数函数的拟合效果较差。综合上述结果，一元线性模型和二项式模型对本次样地中樟树的拟合效果最佳。

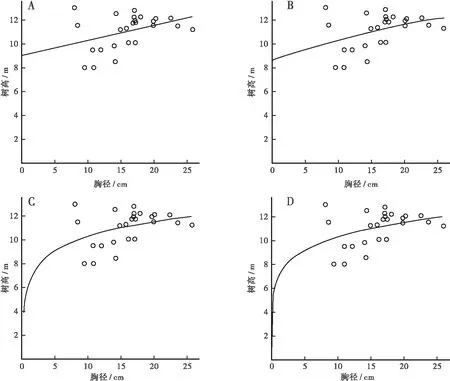
注：A为一元线性模型，B二项式模型，C对数函数模型，D指数函数模型

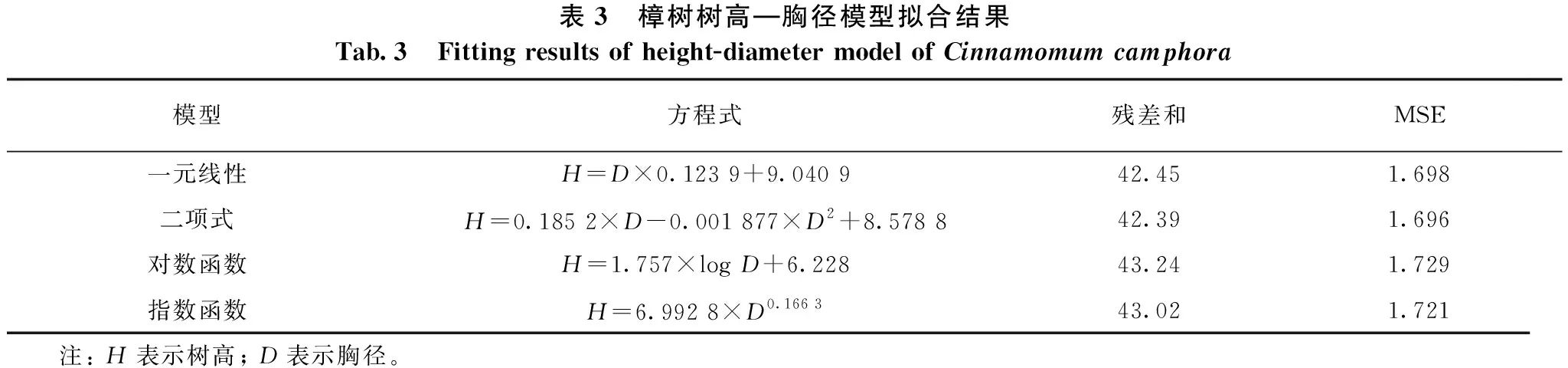
表3 樟树树高—胸径模型拟合结果Tab.3 Fitting results of height-diameter model of Cinnamomum camphora模型方程式残差和MSE一元线性H=D×0.123 9+9.040 942.451.698二项式H=0.185 2×D-0.001 877×D2+8.578 842.391.696对数函数H=1.757×log D+6.22843.241.729指数函数H=6.992 8×D0.166 343.021.721 注: H表示树高; D表示胸径。

4 结论与讨论

(1) 通过分析汉寿县樟树林的调查数据，表明该地区樟树林的胸径、树高和冠幅等林分因子均呈非正态分布。TSTRAT分层算法结果表明该林分的林层结构较为单一，单株间竞争强度较高。构建的树高-胸径模型表明二项式模型和一元线性模型的拟合效果最好。

(2)林层的定性划分方法多种多样，有基于不同演替时期森林外貌特征的方法、克拉夫特分层法、国际林联的优势高划分法等，我国也制定了林层划分的相关标准(GB/T26424—2010)。这些方法虽然有一定的量化变量，但变量得出的结果不能同时准确得出林层划分数量和位置，需要进行人为主观划分[1]。

(3)TSTRAT分层算法以林层中最高树冠长和所有林木枝下高作为划分林层的依据，其选取的变量具有一定的生物学意义，同时能够清晰知道林层的数量和位置。本研究运用TSTRAT分层算法精确计算了樟树林的林层结构，并鉴定为单层结构，对于林相改造具有重要指导作用。同时，该方法也存在一定的不足之处，没有考虑到相对多度、相对显著度及重要值等参数。此外，新兴的遥感划分法能够在更大尺度、更高分辨率下量化结构特征，是未来应用的主要技术手段[16-17]。树高—胸径模型在计算树干材积、生长和收获模型等应用中具有重要的作用，其中最小二乘法是进行拟合时最常用的方法，在众多阔叶树种的树高—胸径模型拟合中取得较好效果[18-19]。

(4)由于样地生境异质性不强，异常数据较少，因此二项式模型和一元线性模型均获得了较好的拟合效果，但未来的研究中应该考虑环境异质性较高的樟树个体，同时增加研究样本和备选模型，进一步提高模型的适用范围。

本研究分析了汉寿地区阔叶树公益林的垂直结构，筛选了樟树的树高—胸径模型，为地区林相改造、树高预测、生物量反演等研究奠定一定的基础。