改进CK-means+算法及并行实现
邵金鑫,行艳妮,南方哲,赵 鑫,马廷淮,钱育蓉+
(1.新疆大学 软件学院 新疆维吾尔自治区信号检测与处理重点实验室,新疆 乌鲁木齐 830046; 2.南京信息工程大学 国际教育学院,江苏 南京 210044)
0 引 言
K-means算法因其原理简单、易实现、运行高效等优点成为大规模数据的常用算法[1-3],但人为设定K-means算法初始聚类中心点和聚类数目,使聚类结果不稳定,以至精度低、收敛慢。针对K-means算法的改进工作大都关注于优化聚类簇数和中心点以及高效处理大规模数据这两个方面[4-12]。文献[13-17]使用预划分数据集和全局优化思想来优化初始值选取过程。文献[18]使用Kd树划分数据集,提供选取初始中心点的依据。但是Kd树较慢的建树速度随着数据量增大会进入瓶颈期。文献[19]将最大最小距离算法与禁忌搜索算法相结合,优化初始中心点。文献[20-26]将预聚类结果作为K-means算法的输入,但算法复杂度增加。以上方法分别存在处理大规模数据困难、复杂度高、通用性能差等问题。因此,本文提出改进的CK-means+算法,通过优化Canopy算法和均值计算法,解决K值不确定性和选取初始中心点的问题,并结合Spark平台在UCI数据集上,从3个方面对比其它算法的性能。
本文的主要贡献是:
(1)解决了Canopy算法中阈值T1和T2难以确定的问题,自适应得到阈值T2;
(2)采用改进Canopy算法得到聚类数目,均值计算法得到初始中心点,对K-means算法进行改进;
(3)设计并实现Spark下K-means算法的并行策略,使其更有效地适用于大规模数据的聚类处理。
1 相关技术
1.1 Spark平台
Spark[27-29]是由UC Berkeley的AMPLab提出的一种由Scala语言实现的大数据计算框架,既兼容Hadoop中MapReduce的可扩展性和容错性等优点,同时引入内存计算的概念。为加快Spark处理数据的运算速度,将数据存储在HDFS中,Spark和HDFS结合使用,并采用Spark的YARN模式管理资源调度。Spark的YARN模式如图1所示,它通过ResourceManager来申请资源,该资源管理器启动NodeManager来管理从属节点。在YARN模式下,Spark基于HDFS来存储操作数据,这不仅具有高效、快速处理大数据的优势,而且还充分发挥了HDFS数据存储的优势。
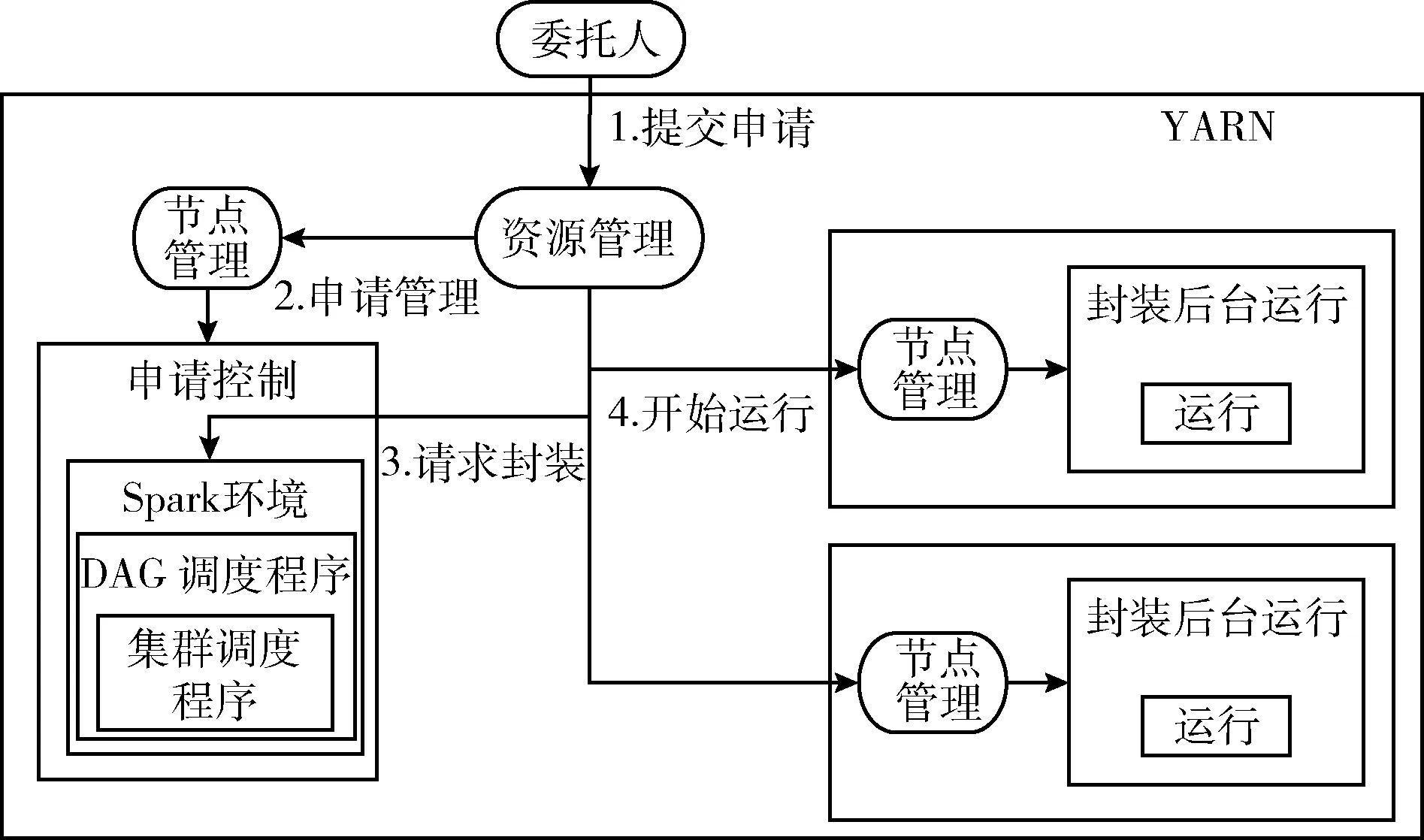
图1 Spark的YARN模式资源管理调度
1.2 K-means算法概述
K-means算法是数据挖掘领域的重要算法之一,它的特点是不受监督,原理是根据数据集特征的相似度对数据进行分类。K-means聚类算法的定义为:假设需要聚类的数据集X中有n个数据点,将其分为k类,用向量X=x1,x2,x3…xn表示待分类数据集,用向量C1,C2,C3…Ck表示k个数据集合,k∈{1,2,3,…K}, 以数据集X为例,有n个点,m个属性,以矩阵形式表示:
(1)划分待分类数据集

(1)
Xn=[x1n,x2n,x3n,…,xmn]T(n∈{1,2,3,…,N},m∈{1,2,3,…,M})
(2)
(2)选取初始中心点

(3)
Ck=[c1k,c2k,c3k,…,cmk]T(k∈{1,2,3,…,K},m∈{1,2,3,…,M})
(4)
(3)计算欧氏距离和选择最小距离
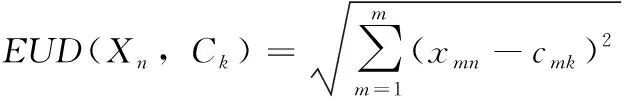
(5)
Xi={Min(EUD(Xn,Ck))} (i∈{1,2,3,…,N},n∈{1,2,3,…,N})
(6)
(4)成本损失函数最小化
(7)
1.3 Canopy算法原理
Canopy算法是由Mccallum等提出的无监督预聚类算法,用于高维度的大数据预聚类分析。它可以仅仅进行距离计算,就把初始数据集进行划分为多个可重叠的子集,从而可以消除数据集中的噪声点或离群值,因此,经过Canopy算法预处理后,K-means算法迭代次数降低,聚类耗时减少。原理是将Canopy算法对数据集做初步聚类结果的中心点作为K-means算法的初始质心。使用Canopy算法对数据集分类要预先设定两个距离阈值T1、T2,选择初始中心点,再计算数据点与初始中心点之间的距离,根据距离阈值将样本划分为相应的聚类。Canopy算法具体如算法1和图2所示。
Algorithm1: Canopy clustering algorithm
Input: Data setsX
Output: The cluster numberKand initial cluster centers of datasets
(1) initialize the ArrayList and setT1,T2
(2) select initial data pointsxrandomly
(3) FOR(each dataxi∈X){
(4) IF(data setsX!=null)
(5) {computed;
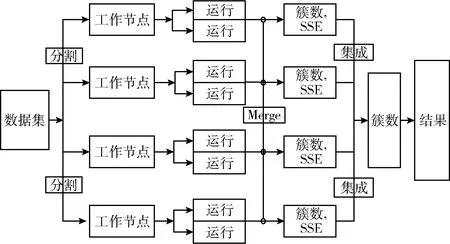
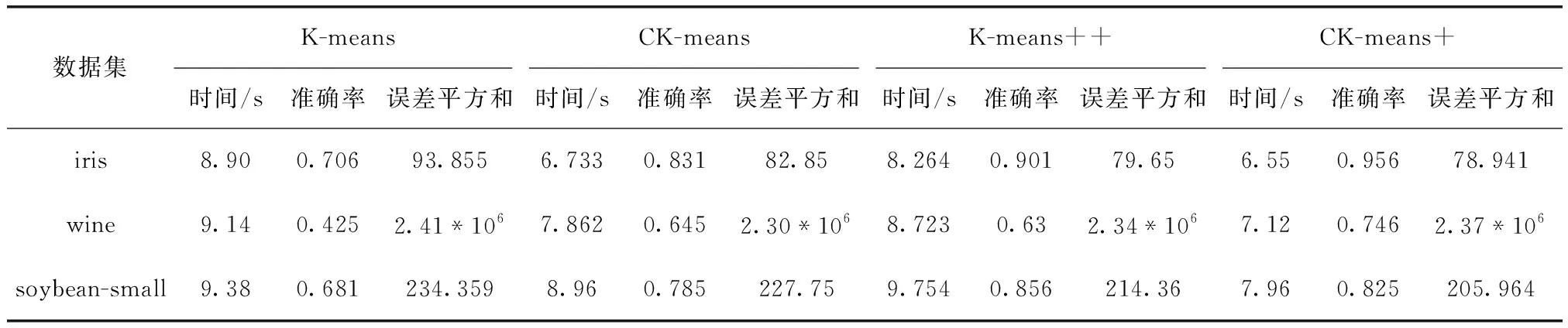
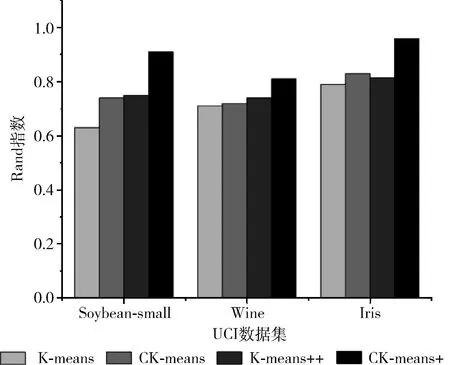
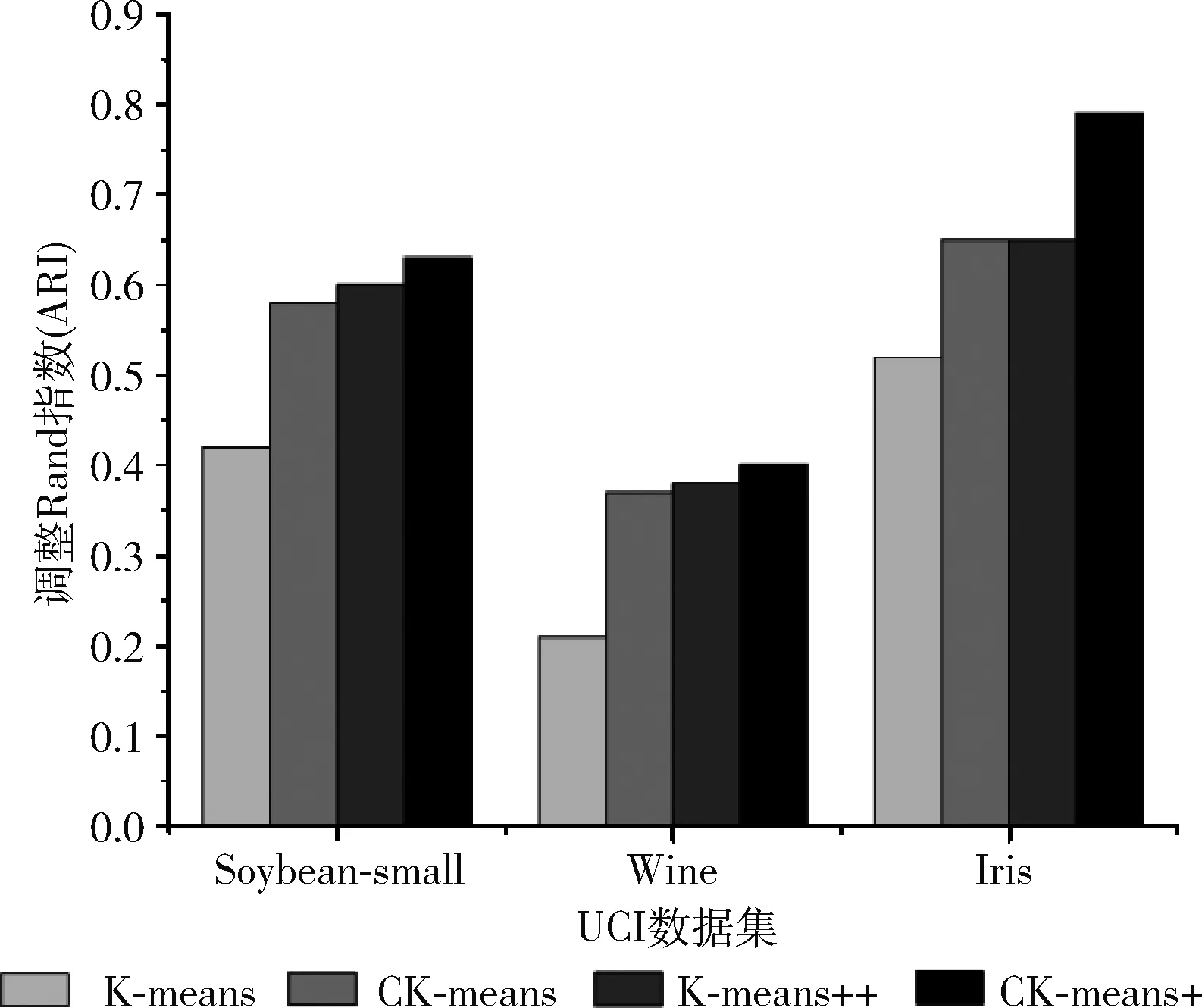
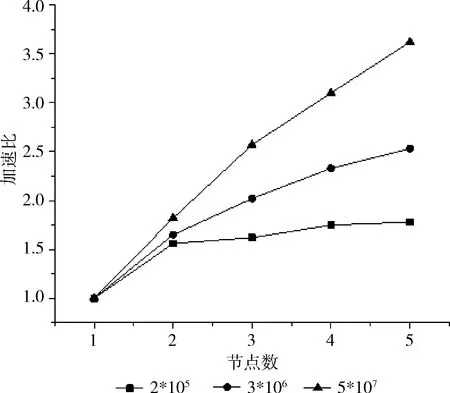
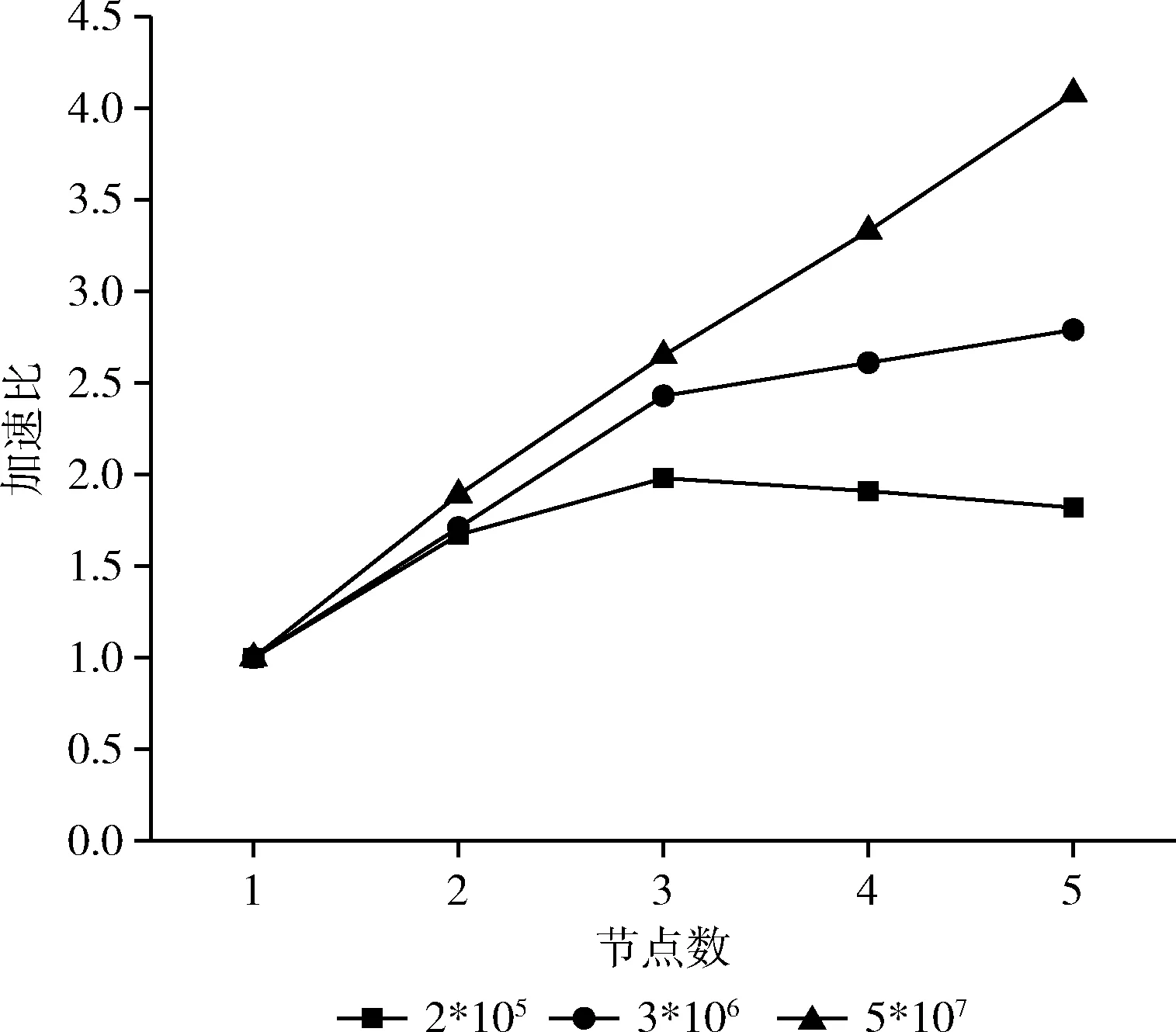
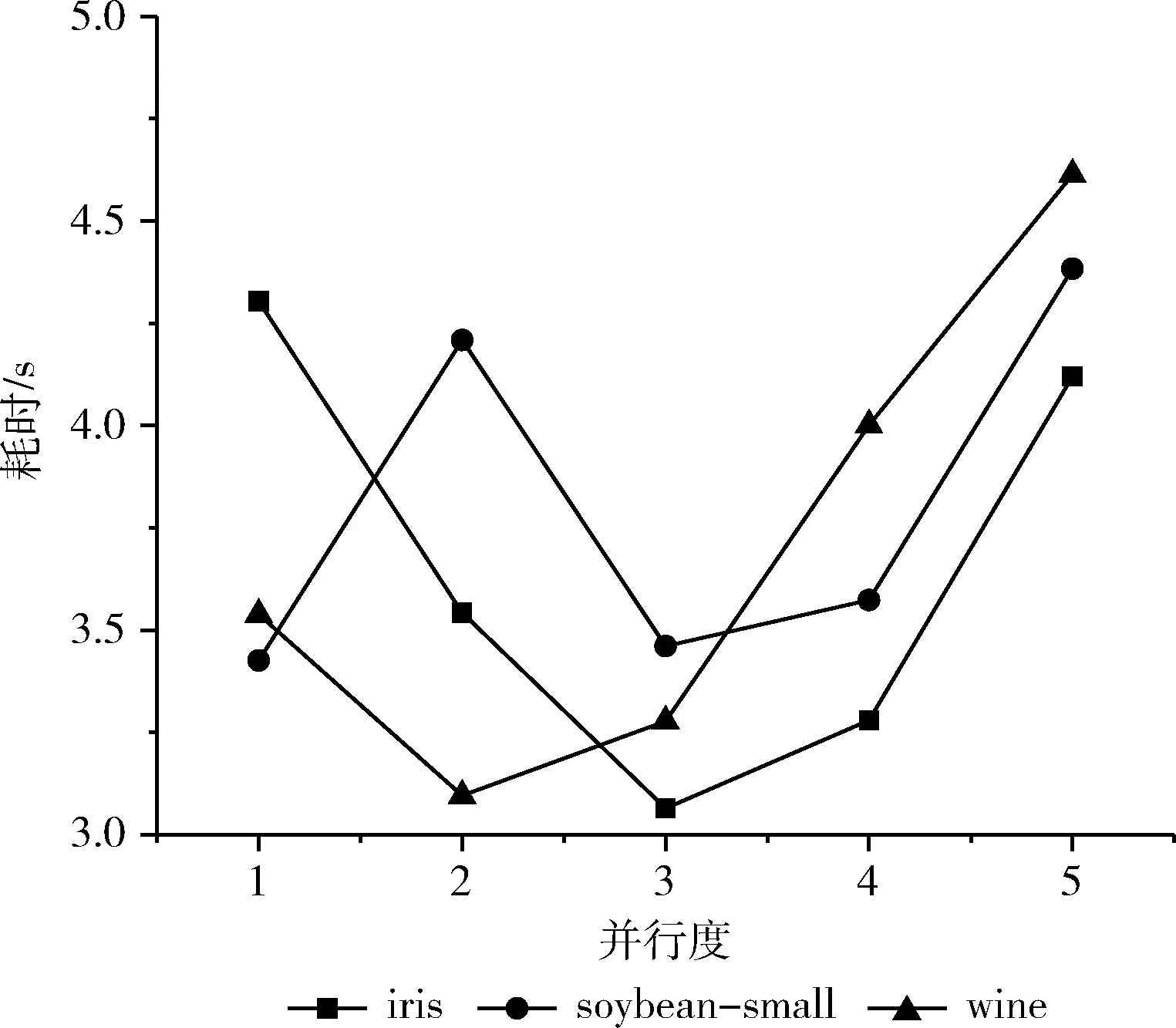
(6) IF(d (7) Canopy setsci←dataxi; (8) }; (9) ELSE IF(d (10) remove dataxifromX; (11) } (12) } (13) ELSE { (14) break; (15) } (16) } (17) END FOR (18) PRINTF(valueK, Initial Center); 图2 Canopy算法流程 CK-means+算法的改进思路为:采用精度不高的Canopy聚类和均值计算法对源数据集进行处理,将输出的结果提供给K-means作为初始值选定的参考,从而消除初始中心点和聚类数目K选择的不确定性。 因此在本节中将首先阐述优化Canopy算法的思想,接着介绍使用Canopy和均值计算法优化 K-means算法的初始阶段。 Canopy算法的距离阈值T1和T2具有很大的随机性,一般都根据经验给定,这对最终结果的准确性和效率有很大影响。如果将阈值设置得太大,则可能会将不同类数据分到同一个Canopy中,反之阈值过小,则有可能会将同一类数据分到好几个Canopy中。因此本文提出一种改进Canopy算法。考虑到Canopy算法阈值的不确定性,以及阈值T2对Canopy算法最终输出K值的影响,本文算法主要考虑阈值T2的设定,针对源数据集,计算所有点之间的距离之和,自适应得出阈值T2。 改进Canopy算法步骤为: 步骤1 创建一个空的Canopy集合ArrayList,将数据集X转化为 步骤2 计算数据集中数据点间的欧式距离之和,对所得到的距离进行数学运算,得到阈值T2,作为Canopy算法的输入; 步骤3 依次读取数据集X中的数据点,将第一个数据点作为第一个Canopy的中心点,计算数据集X中数据点与中心点之间的欧式距离,并度量相似度; 步骤4 若计算出的距离小于阈值T2,将该数据点从数据集中X剔除,划分到上述中心点的Canopy集合中;反之,依次读取下一数据点; 步骤5 迭代进行步骤3、步骤4,直到数据集X为空,输出聚类数目K。 在K-means算法中,合理选择初始中心点和聚类数目K可以避免算法陷入局部最优并且能够有效减少算法迭代次数,本文采用Canopy算法和均值计算法解决该问题。 首先执行改进Canopy输出聚类数目K;再者对源数据集进行平均值计算,依据其均值对数据集排序,同时考虑Canopy算法输出的聚类数目K,将源数据集划分为K个子集,计算每个子集的平均值,取最接近平均值的数据点作为K-means算法的初始中心点输出;最后将K和初始中心点作为K-means算法的输入执行K-means算法,CK-means+算法流程如图3所示。 CK-means+算法如算法2所示,执行步骤如下: 步骤1 从第(1)行到第(20)行,完成Canopy算法阈值T2以及聚类数目K的确定,通过对Canopy算法进行优化,读取数据集X进行预聚类过程得到聚类数目K,作为K-means算法的一个输入; 步骤2 执行第(22)至(32)行的任务,计算数据并进行排序,并获得初始中心点作为K-means算法的另一个输入; 步骤3 完成第(33)行至第(48)行CK-means+算法的计算,输入初始中心点和聚类数K,根据欧几里得距离测量相似度,依次计算数据点与中心点的距离,将数据点分到最小距离的聚类中,计算群集中每个子集之间的平均距离,并计算新的群集中心点; 步骤4 将更新后聚类中心的SSE值与初始中心点进行对比,如果收敛,则结束,将聚类结果输出;否则迭代执行步骤3。 图3 CK-means+算法流程 Algorithm2: Improved K-means algorithm Input: Data setsX Output: Clustering results of data sets (1) initialize the ArrayList (2) compute the valueT2 (3) FOR(each dataxi,xj∈X){ (4)sum←computedij(data pointxitoxj) (5) } (6)T2←sqrt(sum/2) (7) // (8) Canopy input(Data setsX,T2) (9) select initial data pointsxrandomly (10) FOR(each dataxi∈X){ (11) IF(X!= null){ (12) computed; (13) IF(d (14) Canopy setsci←dataxi (15) removexifromX (16) } (17) } (18) } (19) END FOR (20) PRINTF(valueK) (21) // (22) compute the average value of each data point (23) FOR(each dataxi∈X){ (24) computedi(avg) (25)di(avg)=(w1*x1+w2*x2+…wm*xm)/m (26) } (27) sortXbased ondi(avg) (28) Divide the data intoKsubsets (29) Calculate the mean value of each subset (30) Take the nearest possible data point of the mean as the initial center point for each data subsets (31) print(initial Centers) (32) // (33) K-means input(ValueK, initial Centers) (34) FOR(each dataxi∈X){ (35) IF(data setsX!=null){ (36) For(each dataxi∈X){ (37) calculate the Euclidean distancedik(dataxito initial centersk) (38) IF(MinDis(k)==dik){ (39) centerk←xi (40) } (41) } (42) } (43) } (44) END FOR (45) compute New Centerci= (46) Mean(sample(xi&& (xi∈ci))) (47) } (48) PRINTF(Clusterci); 在K-means算法中,算法时间复杂度可以表示为O(K*N*T), 其中K是聚类数,N是聚类数据集的数据量,T是迭代次数。本文提出的CK-means+算法的时间复杂度取决于以下因素:聚类数K、数据集的数据量N、迭代次数T以及并行数p,并且Spark并行算法将数据集分割为p个数据块,每个数据块的数据量大小为N/p,每个并行数据块单元的任务是将所有数据点分配到相应类,并计算出新的中心,时间复杂度可以表示为O(K*N/p*T), 因此 CK-means+算法的时间复杂度主要取决于数据集的数量,并且因为CK-means+算法的输入参数最佳,算法迭代次数比K-means算法迭代次数要少。因此CK-means+算法具有良好的时间性能。 结合Spark并行编程模式,设计Spark框架下CK-means+算法的并行实现。CK-means+算法实现如图4所示,主要分为3个阶段:分割数据集、聚类并行化和聚类结果合并[30,31]。 图4 基于Spark的CK-means+算法 在算法运行之前,上传数据集到HDFS,HDFS把数据集分割为数据子集,Spark集群则会根据RDD的血统生成DAG图,通过DAGScheduler调度器,根据加载的数据子集,在Executor里创建任务,再将计算资源分配给各个节点,具体步骤如下,并行CK-means+算法如算法3所示: 步骤1 采取HDFS的数据分区方法将数据集X分成p部分,将X/p的数据块分配给每个节点;主节点将Ca-nopy算法预聚类输出的初始中心点和聚类数目都传输给各个节点。 步骤2 在每个工作节点中,Canopy算法对分割后的数据集进行预处理,并输出初始中心点和簇数作为CK-means+算法的输入。K-means算法迭代计算各个数据子集与初始中心点的欧氏距离,计算每个聚类点到中心点的距离的和SSE,并标记每个点的类别。 步骤3 将聚类结果与并行结果进行集成。并行化后获得的聚类中心点需要聚合。聚合有两种类型:最小化ASSE(平均SSE)和分层聚合。为了确保聚类结果的准确性,本文使用最小化ASSE方法来聚合上一步中计算出的结果。也就是说,SSE和群集中心将进行迭代,直到SSE收敛为止。 在Spark上算法实现如下: Algorithm3: Parallel CK-means+algorithm in Spark Input: DatasetsX, Filepath, partition Output: Clustering results of data sets (1) val sc←new SparkConf(conf) (2) val input←sc.textFile(Filepath,partition) (3) val dataArray←data.map{ // Processing the data set (4) val label←line.split(",").take(1) (5) val pair←line.split(",").drop(1).map {_.toDouble} (6) (lable,pair) (7) } (8) Canopy(DatasetsX) (9) PRINT(valueK,initialCenters) (10)K-means(DatasetsX, valueK,initialCenters) (11) PRINT(Clusterci) 实验环境采用1个主节点和4个从节点的模式构建两个计算集群:Hadoop集群和Spark集群。表1显示每个节点的角色。配置最高的计算机是Master和NameNode节点,普通节点为Worker和Datanode节点,各个节点配置信息见表2。 表1 集群节点配置角色 表2 实验环境配置 本文所用实验数据是UCI机器学习标准数据库,选择下列3个数据集进行实验:soybean-small、iris、wine见表3,每个数据集都有不同的样本数量,同时每个样本有不同数量的属性,进而去测试改进算法的有效性。 表3 UCI数据 CK-means+算法的聚类效果由以下几个参数衡量:完成聚类所需的时间、误差平方和(the sum of squared errors of the clustering results,SSE)、聚类结果准确性,以及衡量聚类结果有效性的几个参数:Rand指数和调整Rand指数(ARI)。 本文采用4种不同的聚类算法K-means算法、CK-means算法、K-means++算法和CK-means+算法)处理UCI数据集并比较聚类效果。以下数值为算法进行多次实验后所取得的平均值,根据表4的数据分析和比较,可以得到以下结论: (1)K-means算法和K-means++算法执行花费时间较长,是因为传统方法是随机选择初始中心点,导致算法达到收敛状态也就是稳定时迭代次数更多,因此算法聚类过程花费的时间更长。K-means ++算法的时间复杂度高,因此其执行时间也更长。使用Canopy算法预处理的K-means算法聚类时间明显优于K-means算法,是由于该算法预先通过Canopy算法对数据集进行处理,再完成数据集的聚类,算法到达稳定状态时的迭代次数会减少,因此它比K-means算法表现更优; (2)分析聚类算法的误差平方和,可以看出CK-means+算法聚类效果最佳。K-means算法随机选择初始中心点,具有最大的SSE,并且聚类效率较差; (3)从聚类结果的准确性来看,CK-means+算法的准确性比K-means算法高23.8%,比CK-means高8.87%,比K-means++算法高4.53%。因此可以看出CK-means+算法的性能优于其它3种算法; (4)图5和图6显示4种算法聚类结果的参数(Rand指数和调整Rand指数)比较。通过计算样本的预测值和实际值的相似度来获得Rand指数。调整后的Rand指数类似于Rand指数,值越接近于1,聚类结果越好。从图中可以看出,CK-means+算法的参数相较于K-means算法、CK-means算法和K-means++算法表现最优,可以看出CK-means+算法在各个方面都具有良好的聚类效果。 表4 聚类算法性能对比 图5 Rand指数对比 图6 调整Rand指数对比 在并行计算领域,加速比用于表示并行计算与相应的顺序执行相比的运行速度,来衡量并行程序的性能和效果,加速比定义为式(8) Er=Ts/Tr (8) 其中,Ts表示算法顺序执行时所需的时间,Tr表示算法在计算节点为r个的Spark集群中运行所需的时间。 当数据作为RDD加载时,它可以进入单个计算节点的内存进行聚类过程,因此,算法可以单独在单个计算节点上运行,即使在顺序执行时,算法也可以运行,但是当数据被分割并且分配给多个计算节点时,随着计算节点的增加,各个节点间的开销也会增加,因此引入更多数据节点来进行测试。 为了并行验证CK-means+算法的性能,在实验中选择Spark MLlib中的K-means算法作为参考,以比较这两种算法的加速比。 实验中,Spark集群设置1~5个并行节点,2*105、3*106、5*107的数据量。HDFS作为文件系统,主节点运行Master、DataNode和Slave,从节点只运行Slave和DataNode。图7和图8描述两种算法在不同数据量下节点数与加速比的关系。可见,算法的加速比都近似线性。 图7 MLlib K-means算法在Spark下的加速比 图8 CK-means+算法在Spark下的加速比 在数据量较小时,MLlib K-means算法加速比增长缓慢,而CK-means+算法在节点数超过3时,加速比甚至有所下降。然而当数据量达增加到5*107时,节点数从2个增加到5个时,MLlib K-means算法的加速比从1.56提高到3.76,CK-means+算法的加速比从1.8提高到4.0。加速比明显增加。由此可见CK-means+算法在处理大规模数据时的优势。 为了测试不同并行度下CK-means+算法的聚类时间,实验在UCI数据集上测试CK-means+算法在并行度为1至5时的耗时。 如图9所示,随着并行度增加,聚类算法的时间消耗总体呈现出先减少后增加的趋势。当并行度为2或3时,该算法花费时间最短,而当并行度为4或5时,该算法的时间消耗增加。计算时间减少的原因如下:随着并行度增加,算法时间消耗由于并行处理数据而减少;通过并行迭代计算数据集与中心点间的距离,缩短算法的消耗时间。计算时间增加的原因如下:随着并行度的增加,过多的并行度导致多个结果进行最终合并,从而增加了算法的运行时间。 图9 CK-means+算法在不同并行度下的耗时 为了解决K-means算法中初始中心点和聚类数K值的不确定性的问题,本文提出基于Canopy预聚类算法和均值计算法的CK-means+算法。在UCI数据集上相较于K-means++算法、CK-means算法和K-means算法,CK-means+算法的聚类准确率分别平均提高7.03%、8.87%和24.1%,效率更高。并在Spark内存计算框架下,对CK-means+算法进行并行化编程,验证其对处理大规模数据的适用性。该方法结合优化Canopy算法和均值计算法两种方法,分别解决聚类数K和初始中心点的问题,提升了聚类算法的准确性和效率。 未来的工作将会集中在两个层面,第一个层面是考虑聚类算法数据输出的结果,准确高效整合聚类结果,提高聚类算法的准确率和效率;第二个层面是由于大数据格式的多样化,对数据处理的准确性和实时性有更高的要求,因此下一步考虑对数据进行降维,实现更高效的数据聚类。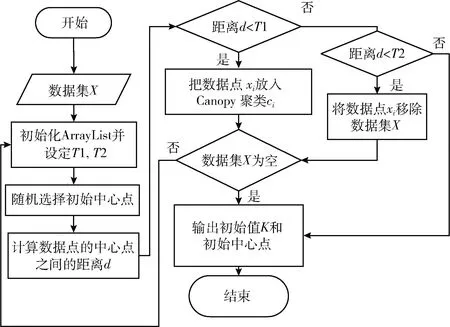
2 CK-means+算法原理
2.1 Canopy算法的优化
2.2 CK-means+的改进

2.3 CK-means+的算法复杂度
3 实验实现
3.1 CK-means+算法在Spark下的并行实现
3.2 环境配置
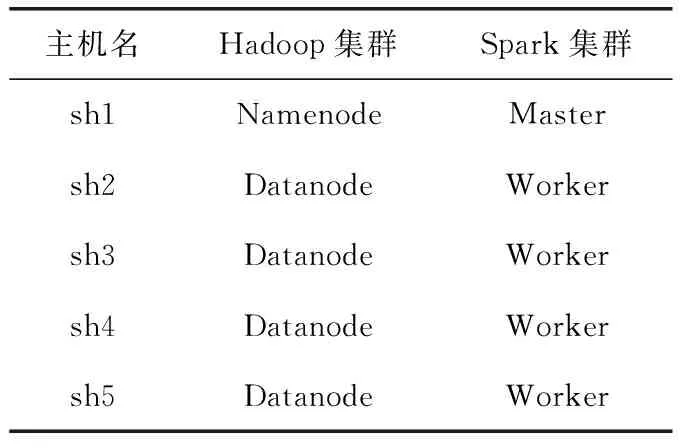
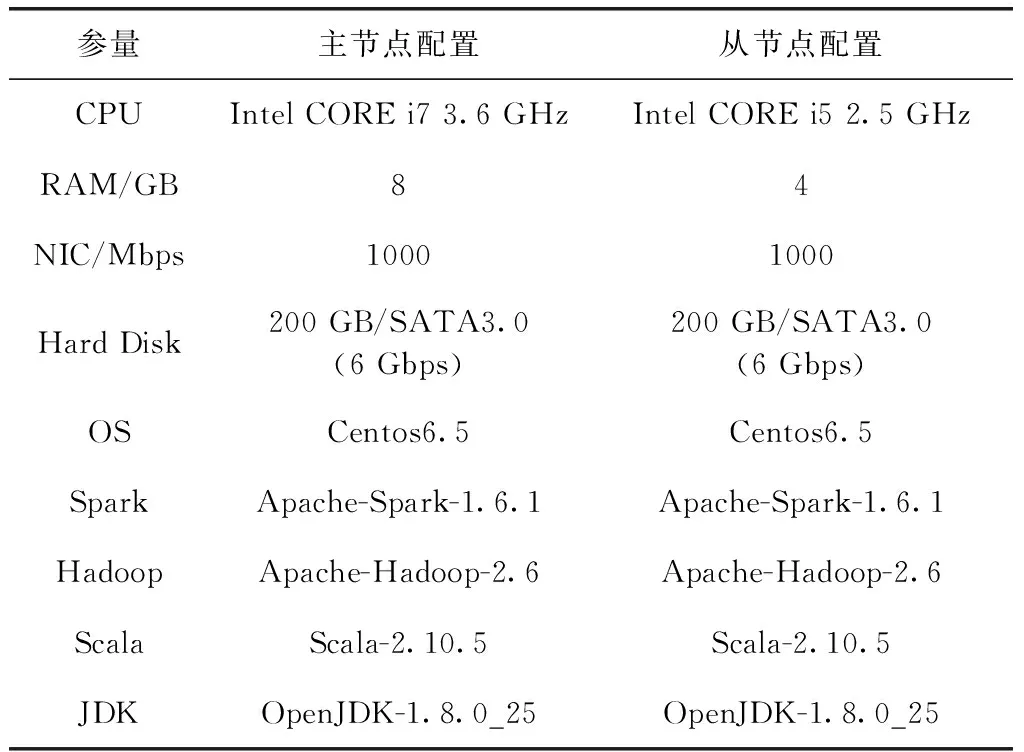
3.3 实验数据集
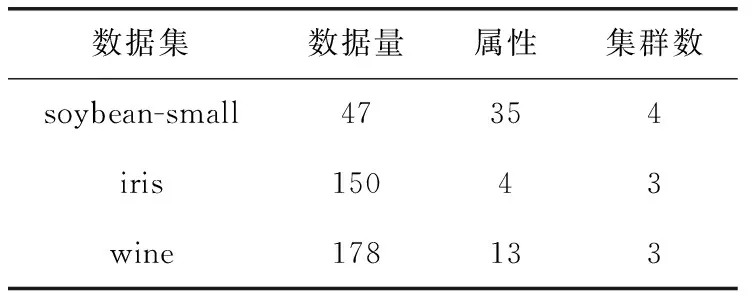
4 实验分析
4.1 性能对比
4.2 加速比分析
4.3 并行度对比
5 结束语

