基于滤波器-光谱数据降维的指甲地区识别
古锟山,王继芬*,曾啸虎
(1.中国人民公安大学 侦查学院,北京 100038;2.酒泉卫星发射中心,甘肃 酒泉 735000)
随着法庭科学检验技术的不断发展,所收集的生物检材从传统的尿液、唾液以及血液逐步发展到头发、汗液、眼泪、指甲等[1]。与传统的生物检材相比,汗液和眼泪所需检材的量更少,头发和指甲则具有保存时间长、容易收集、抗污染能力强、对待测目标物稳定等优点[2-3]。与头发样本相比,指甲样本的生长速度更加稳定,不受黑色素等因素的影响,因此检测更具可靠性和稳定性[4]。
在法医和刑事案件中,指甲作为一种生物物证具有重要作用。与人体的其他组织相比,即使是少量的指甲样本也能够包含个体的相关生物信息。此外,指甲样本的采集是非侵入性的,样本可以在室温下储存,且指甲成分的稳定性强,其中所蕴含的生物信息可以帮助识别嫌疑人。目前指甲检验在案件侦查中的作用主要有以下几点:(1)通过对指甲中残留的组织或血液进行DNA 检验,提供犯罪嫌疑人的相关信息,为案件侦查提供方向;(2)对指甲进行毒理化检验可以确认嫌疑人是否有吸毒等行为;(3)在服毒自杀的案件中,对指甲进行检验有助于确认案件性质;(4)对于抛尸案件来说,指甲检验可对无名尸源进行溯源调查[5]。
目前对于指甲的检验主要采用以下方法,一是利用气相色谱-质谱联用(GC-MS)等技术对指甲中的违禁物品进行检验分析[6-7];另一方面是利用元素分析-稳定同位素比质谱技术(EA-IRMS)对指甲中的氢、氧稳定同位素比值进行检验从而进行地区的区分[8-12],但该方法检测时间长、仪器昂贵,不能满足公安机关快速无损检验的需求;还有一种是利用光谱技术对指甲进行检验。傅里叶变换红外光谱具有分析速度快、操作简单、能够提供待测物的丰富结构信息等优点,是一种很有前途的非破坏性技术,被广泛应用于各微量物证的检验鉴定[13]。由于每个地区的环境气候不同,同时不同人指甲中的蛋白质、含水量及微量元素含量均有所差异[14-15],使得利用光谱检验技术对指甲进行个体识别乃至溯源分析具备一定的可行性,Sharma 等[16]利用衰减全反射-傅里叶变换红外光谱(ATR-FTIR)采集了100 份指甲样本的光谱图(男女性各50 份),利用主成分分析进行数据降维后以偏最小二乘判别分析模型对指甲样本的性别进行识别。实验结果表明,数据降维后模型的识别率得到提升,总体分类识别率为95%,其中男性样本的识别率为90%,女性样本的识别率为100%。这一研究充分证明红外光谱技术结合化学计量学能够实现对指甲中生物信息的区分。
实际获得的红外光谱数据除了纯光谱以外还存在大量的噪声、基线漂移等干扰信号,这些干扰信号会降低原始谱图的信噪比,影响红外光谱的精度以及导致模型过拟合现象的发生[17]。与此同时,随着样本量的增大,光谱数据的维度也随之增大,这导致光谱识别模型的运行时间增加,识别率降低。因此,建模前对光谱数据进行降噪和数据降维处理非常必要。
滤波器是一种信号过滤元件,其本质是一个选频装置,通过设置滤波器使特定频段的信号通过,可极大地滤除其他频段的成分,实现滤除干扰噪声的目的[18]。鞠薇等[19]利用改进阈值提升小波和自适应滤波器对大气红外光谱进行降噪处理后,谱图的噪声明显降低,均方根误差(RMSE)降低了30%,模型运行时间缩短了46%,充分证明利用滤波器对红外谱图进行除噪的可行性。光谱数据降维是对光谱数据进行建模分析的预处理步骤,其过程主要是根据一定的评估准则从原始高维光谱数据集合中选择出解释性最强的变量从而有效地消除冗余和无关的特征,提高模型的识别效率以及准确率[20]。
目前尚未有报道将现代光谱分析技术、光谱降噪技术以及光谱数据降维技术相结合应用于法医人类学领域。指甲所蕴含的有机分子中的化学键或官能团处于不断振动的状态,当用红外光照射有机分子时,分子中的官能团或化学键会发生振动吸收,不同的官能团或化学键吸收的频率不同,同时不同地区的人们由于饮食习惯不同,会导致指甲中所含的生物信息有所区别[12]。本实验从涉案现场收集了指甲样本的红外光谱数据,利用希尔伯特变换滤波器对原始光谱数据进行降噪处理,然后利用主成分分析和偏最小二乘判别分析对样本的红外光谱进行数据降维,并建立朴素贝叶斯以及随机森林模型对处理后的数据进行地区区分。根据模型的识别效果选择最佳预处理方法以及最优识别模型。
1 实验部分
1.1 实验样本
从实际案件中提取的指甲样本共计204 份,其中东部地区32 份,西部地区36 份,南部地区48 份,北部地区40份,中部地区48份。将上述5个地区的样本依次编号为D1、D2、D3、D4、D5。
1.2 仪器及设备
傅里叶变换红外光谱仪(Nicolet6700,Thermo Fisher Scientific,USA),KBr(Thermo Fisher Scientific,USA)。光谱分辨率为8 cm-1,扫描次数为64 次,样品波数采集范围(建模波段)4 000 ~650 cm-1。每个样本采集3次数据,取平均值作为建模分析数据。
1.3 实验预处理
由于指甲形状不同且成分相对比较复杂,在测量采集的过程中存在光谱差异以及因测量时按压力量不同导致的光谱散射影响。这些干扰会影响光谱识别模型的准确性,因此需要对原始谱图进行S-G平滑[21](平滑点数为7,3阶平滑多项式)、基线校准[22]、归一化[23]以及多元散射校正[24]处理,得到初步预处理的光谱数据后再利用希尔伯特变换滤波器对光谱进行降噪处理。
1.4 希尔伯特变换滤波器原理
希尔伯特变换滤波器的工作原理主要是将实数信号变换成解析信号,即把一个一维的信号转换成二维复平面上的信号。复平面上的信号比一维信号更加完整,实信号只是在复平面实轴上的一个投影,复数的幅角和模分别代表信号的相位和幅度[25]。光谱信号通过希尔伯特变换滤波器后会得到一个复平面信号,该复平面信号在实部的投影为降噪后的光谱信号,其信号值为复平面信号每一点的模值,即A(t)=sqrt{x2(t)+Hilbert[x(t)2]},瞬时相位就是虚部和实部在某一时间点比值的arctan。光谱信号通过希尔伯特变换滤波器后不仅能够滤除噪声等的干扰还能丰富谱图的相关信息,提高模型的识别效果。
2 实验建模
2.1 朴素贝叶斯
朴素贝叶斯(Native Bayes,NB)是一种假设每个输入变量都是相互独立的强大预测模型建模算法[26]。其主要过程为给定训练集(x,y),其中每个样本x都包括n维特征,即x=(x1,x2,x3,…,xn),类别标记集合含有k种类别,即y=(y1,y2,y3,…,yk)。对于新样本x,对其类别进行判断就是看它属于哪一类的概率最大,即转化为求解P(y1|x),P(y2|x),…,P(yk|x)中的最大值,也即求出后验概率最大的输出argmaykP(yk|x)。由于,则NB分类器可以表示为:
2.2 随机森林
随机森林是统计学中常用的分类器,能够从训练集中学习特征与标签之间的映射关系,是一种有监督学习算法。随机森林进行分类的主要过程为:(1)在样本的训练集中有放回地随机选样t次,得到t个样本;(2)从样本的所有特征中随机选择x个特征,利用随机选择的特征对所选样本进行决策树的建立;(3)将上述两个步骤重复N次,得到N棵决策树,形成该样本的随机森林;(4)对于新输入的数据,每棵决策树进行决策后会进行投票,得票数最高的即为随机森林判别得到的类型[27]。
2.3 偏最小二乘判别分析
在解决多元线性问题时,多元线性回归会因为自变量之间的相关性导致过拟合现象,而偏最小二乘判别分析(Partial least squares-discrimination analysis,PLS-DA)通过先找到先行独立的替换自变量,使其间相互独立且能够最大限度地反映变量之间的差异,同时剔除不相关的变量,并通过潜在变量进行聚类分析,是一种有监督的模式识别分析方法[28]。
3 结果与讨论
3.1 光谱分析
5 个地区指甲的原始谱图、原始光谱经S-G 平滑处理以及原始光谱经希尔伯特变换滤波器处理后的谱图如图1所示。
角膜屈光手术会造成角膜组织结构和泪液炎症介质不同程度的破坏和改变,从而引起眼表功能改变,导致患者术后不同程度的干眼症状,这已成为术后最常见的并发症[1]。全飞秒激光角膜屈光手术,根据是否制作角膜基质瓣,可分为飞秒激光角膜基质透镜取出术(Femtosecond lenticule extraction,FLEx)[2]和飞秒激光小切口角膜基质透镜取出术(SMILE)[3]。本研究通过比较FLEx与SMILE术后患者早期眼表参数和泪液炎症介质变化,探讨这2种术式对术后眼表情况的影响。
观察图1A 可知5 个地区指甲的红外谱图出峰位置大致相同,只是在峰强上有所区别。其中波数1 500 cm-1左右存在一个强峰,为C—H 的弯曲振动吸收峰;波数1 700 cm-1左右存在一个尖强峰,为C===== O的伸缩振动吸收峰;波数3 000 cm-1处存在一个左高右低的双峰;波数3 250 cm-1左右存在一个中峰,为N—H 伸缩振动吸收峰。峰的具体位置以及波段归属如表1 所示。图1B 谱图的噪声有所降低,但仍然存在毛刺。对比图1B 和图1C 发现,谱图经希尔伯特变换滤波器处理后尖长毛刺的数量明显减少,表明噪声得到了明显改善,但各样本的红外吸收峰仍相互交织,仅凭肉眼区分会产生很大的人为误差,因此需要结合化学计量学对谱图进行分析。
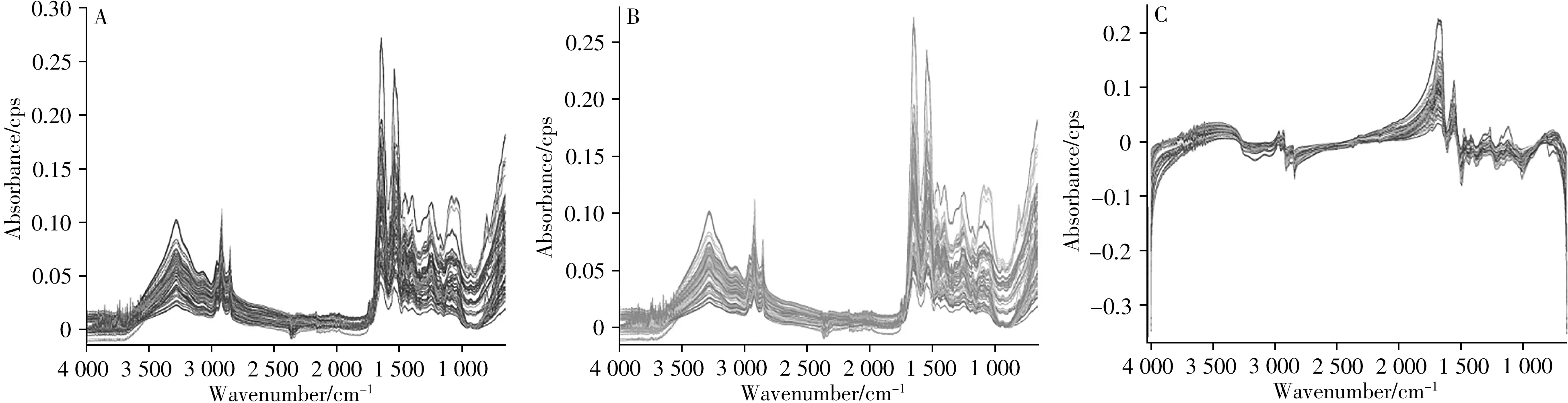
图1 5个地区指甲的原始谱图(A)、原始谱图经S-G平滑处理(B)以及原始谱图经希尔伯特变换滤波器处理的谱图(C)Fig.1 Original spectra(A)of fingernails in 5 regions,and original spectra pretreated by S-G smoothing(B)and pretreated by Hilbert transform filter(C)

表1 光谱峰及其波段归属Table 1 Spectral peaks and their band assignment
3.2 光谱数据降维
主成分分析(Principal component analysis,PCA)通过对协方差矩阵进行特征分解以实现减少数据集维度的同时保留数据中最重要的部分。本实验利用PCA 对原始数据(Original,OG)和经希尔伯特变换滤波器处理后的数据(Hilbert transform filter,HTF)进行数据降维。一般来说所提取的变量的特征值大于1,累计方差贡献率大于85%即可满足建模要求。表2为PCA的总方差解释。

表2 PCA的总方差解释Table 2 Total variance interpretation of PCA
由表2可知,原始光谱和希尔伯特变换滤波器处理后的光谱经PCA提取特征后分别有14和10个特征变量的特征值大于1,且累计方差贡献率分别为98.844%和99.012%,满足光谱建模要求,因此对所提取特征变量进行建模分析。
3.3 朴素贝叶斯建模分析
基于内核函数的不同朴素贝叶斯又可以分为3 种常用模型,分别为多项式朴素贝叶斯(Polynomial naive Bayes,PNB)、伯努利朴素贝叶斯(Bernoulli naive Bayes,BNB)和高斯朴素贝叶斯(Gaussian naive Bayes,GNB)。本实验对3 种朴素贝叶斯模型的分类效果进行比较,通过不断增加迭代数,得到3 种朴素贝叶斯模型的最小分类误差图,实验结果如图2所示。
由图2 可知,3 种朴素贝叶斯模型的最小分类误差随着迭代数的变化呈现不同的波动,且随着迭代数的增加波动逐渐缓和。在波动趋于缓和时,3种朴素贝叶斯模型的最小分类误差值大小排列为:BNB>GNB>PNB,说明PNB 模型更适合于指甲样本的分类,因此本实验采用PNB模型对指甲光谱进行建模分析。
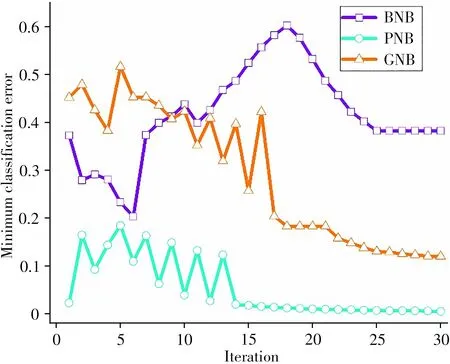
图2 3种朴素贝叶斯模型的最小分类误差Fig.2 Minimum classification error of three naive Bayesian models
分别将原始数据、经希尔伯特变换滤波器处理以及两者又分别经PCA处理的数据进行PNB建模,对5个地区共计204份指甲样本进行分类识别,同时将204份样本按照训练集和测试集3∶1 进行划分,即训练集153 份样本,测试集51份样本。建模效果如图3所示。
由图3可知,PNB模型对样本原始谱图的识别效果不佳,原因可能是原始谱图中含有大量噪声影响了模型的识别率和识别速度。经希尔伯特变换滤波器处理后的原始谱图识别效果优于未处理的谱图,原因是希尔伯特变换滤波器能够将一维的光谱信号转变成二维平面上的光谱信号,降低了原始光谱信号噪声并丰富了谱图的识别信息,提高了模型的识别效果。由于光谱数据降维能够大大降低数据的冗余,提高模型的识别效果,因此上述数据集经PCA数据降维后识别率得到很大提升。根据训练集和测试集的识别率可知,PNB模型对原始数据经希尔伯特变换滤波器处理+PCA数据降维的识别效果最好,其中训练集识别率为87.46%,测试集识别率为84.19%。
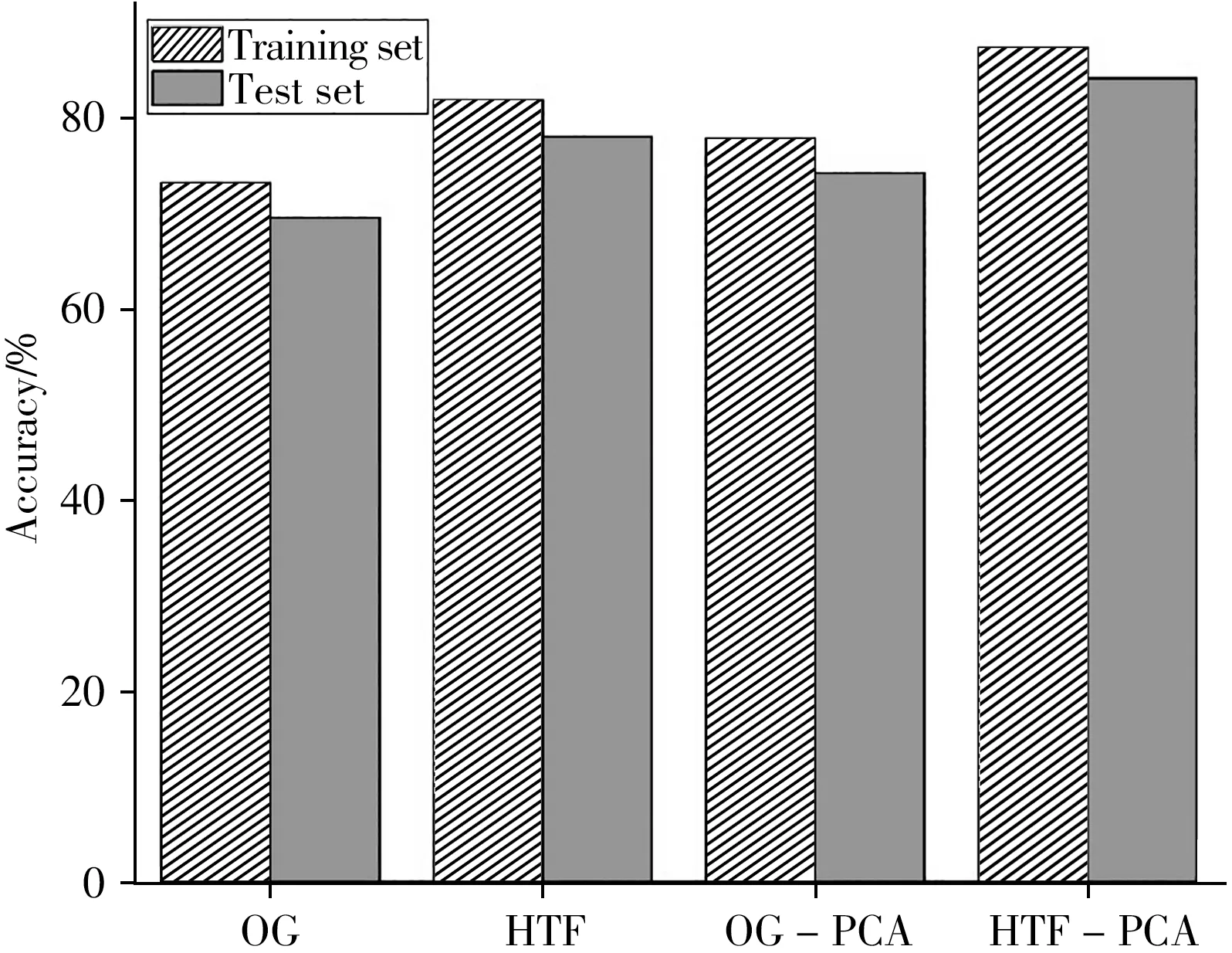
图3 PNB对各数据集的识别率Fig.3 Recognition rate of PNB for each dataset
3.4 随机森林建模分析
在使用随机森林(Random forest,RF)进行样本区分前需对模型的参数进行优化使其达到最佳运行状态。本实验中RF 所需要优化的参数有两个,分别为最大树深度(max_depth)和决策树的个数(n_estimators)。利用OBB error rate 对上述两个参数进行分析,OBB error rate 越小模型运行效果最好。将max_depth 参数值设为1 ~5,n_estimators 参数值设为0 ~260,不同max_depth 下n_estimators 与OBB error rate 的关系如图4所示。
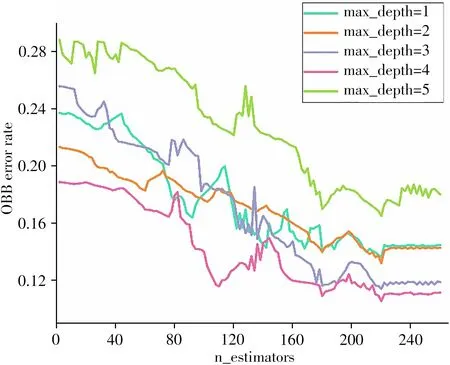
图4 不同最大树深度下的决策树个数与OBB error rate的关系Fig.4 Relationship between n_estimators and OBB error rate under different max_depth
分别将指甲样本的原始数据、经希尔伯特变换滤波器处理后的数据以及以上两者又分别经PCA 处理后的数据进行RF 建模分析,对指甲样本的地区进行区分。RF 模型的训练集和测试集识别率以及误差棒如图5所示。
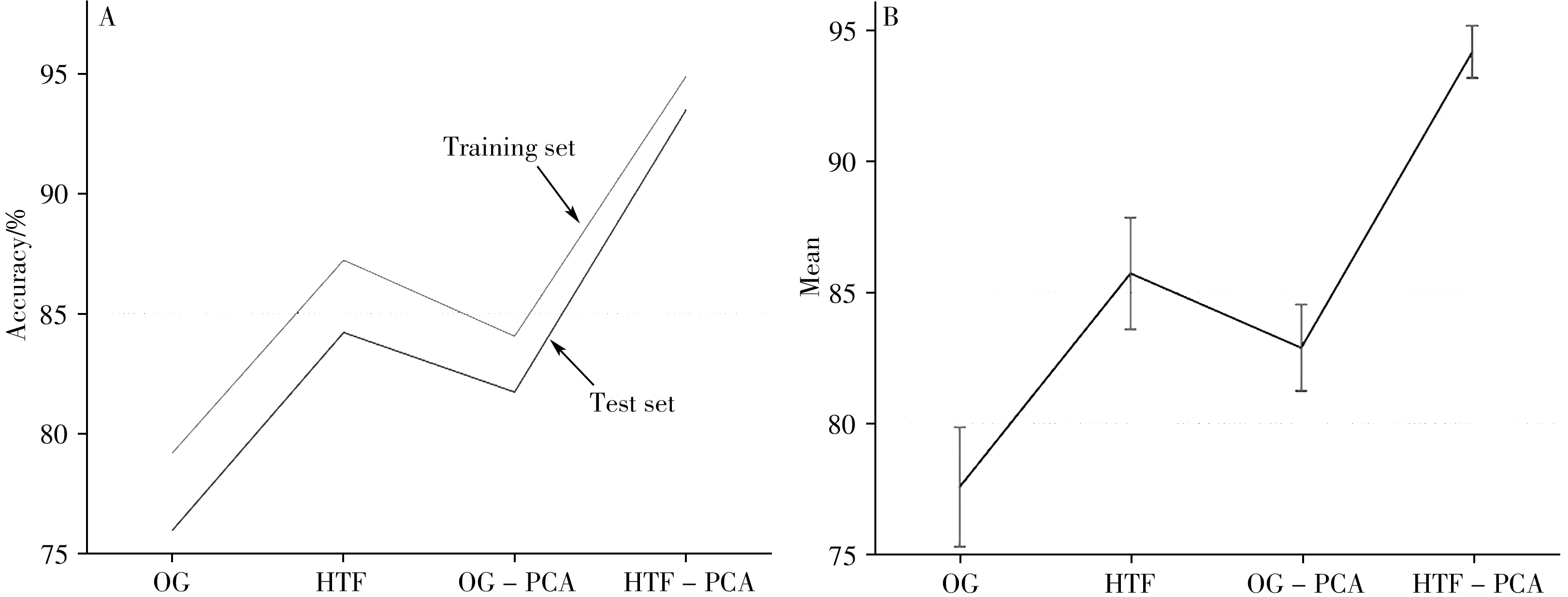
图5 RF模型的训练集和测试集识别率(A)以及误差棒(B)Fig.5 Recognition rate(A)and error bar(B)of training set and test set of RF model
由图5 可得知RF 模型对原始谱图的识别效果不好,充分证明谱图噪声会影响大部分模型的识别率。原始谱图经希尔伯特变换滤波器处理或PCA 降维后识别率有了显著提升,而原始谱图同时经希尔伯特变换滤波器处理和PCA数据降维后的识别效果最佳,训练集识别率高达94.88%,测试集识别率为93.47%。误差棒表示训练集和测试集之间的偏差情况,误差棒越小说明数据之间的波动越小。由图5可知HTF-PCA 的误差棒最小,表明这两种预处理方法结合后的训练集和测试集之间的偏差很小,进一步证明该预处理组合的稳定性优于其他方法。
3.5 偏最小二乘判别分析
最佳因子数的确定是PLS-DA 建模分析的关键问题,影响模型的实际运行效果。本实验通过不同因子数下所建立模型的R2和RMSE 值的大小来确定模型的最佳因子数。原始光谱和原始光谱经希尔伯特变换滤波器处理后的PLS-DA模型的R2和RMSE值随因子数的变化图如图6所示。
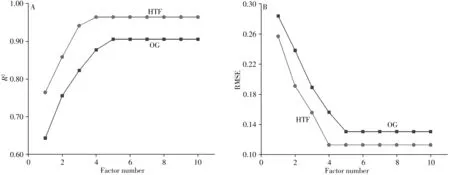
图6 PLS-DA模型的R2(A)和RMSE(B)值随因子数的变化图Fig.6 Variation of R2(A)and RMSE(B)of PLS-DA model with factor number
由图可知,随着PLS-DA 模型因子数的增加,两数据集的R2均逐渐增加后稳定,RMSE 均逐渐减小后稳定,当因子数分别为5 和4 时,OG 和HTF 数据集的R2和RMSE 值趋于稳定。由于因子数过大可能会导致模型的过拟合现象,因此本实验选择OG和HTF数据集的最佳因子数分别为5和4。
分别将指甲样本的原始数据和经希尔伯特变换滤波器处理后的数据在最佳因子数下进行PLS-DA建模分析,对指甲样本的地区进行区分,识别效果如图7所示。
由图7 可以看出PLS-DA 模型对于原始数据的识别效果不理想。对于原始数据,PNB、RF 和PLS-DA 3 个模型均存在同样的问题,充分证明光谱的噪声以及数据的维度会影响模型的运行效果。通过希尔伯特变换滤波器处理后,PLS-DA 模型的识别准确率有了显著的提升,其中训练集的识别率为86.24%,测试集的识别率为84.09%。
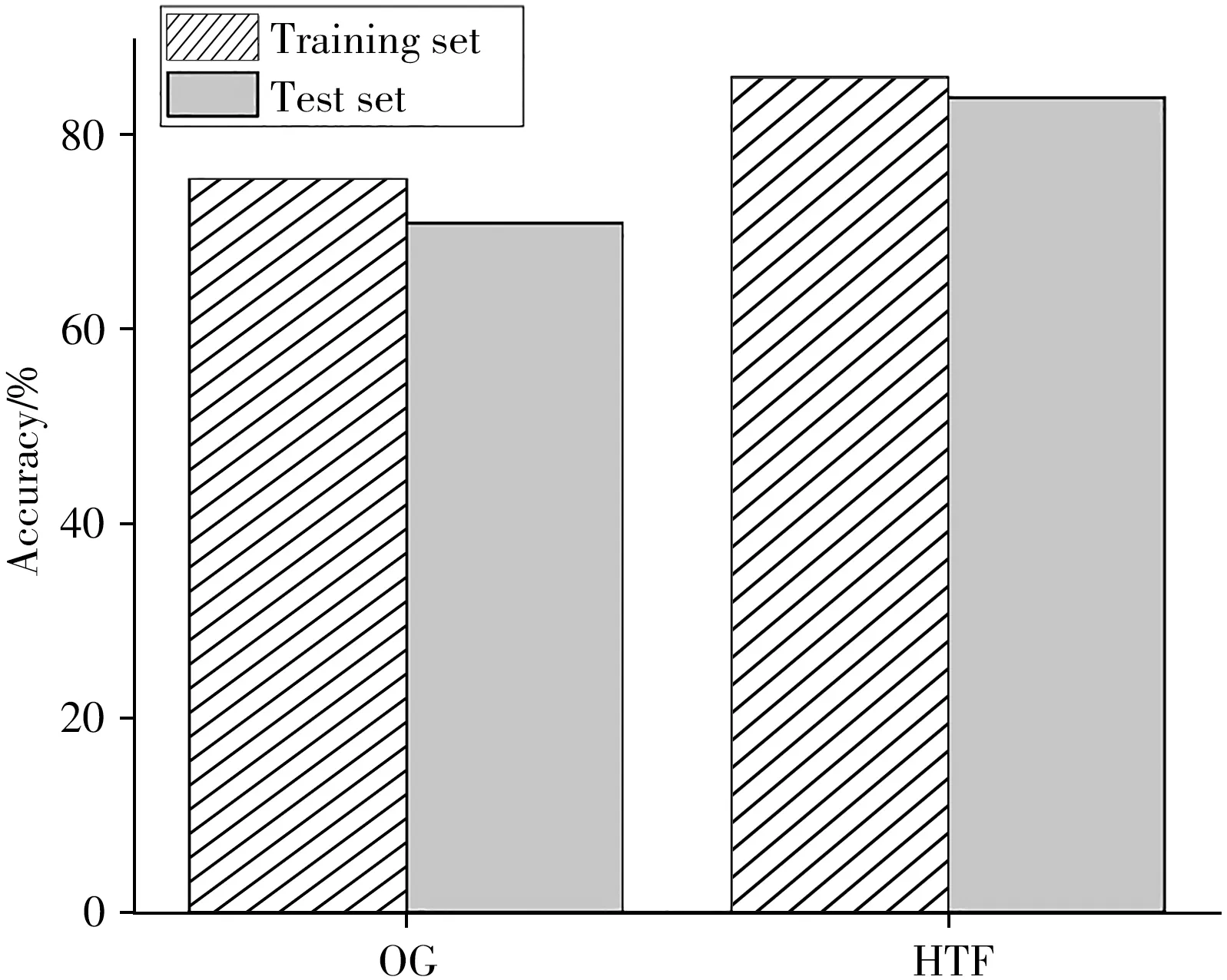
图7 PLS-DA对各数据集的识别率Fig.7 Recognition rate of PLS-DA for each dataset
3.6 3种模型的比较
分别用灵敏度、特异性和精度3 个指标评价3 个模型的性能,一般来说这3 个指标越高,模型性能越好。3 个模型的评价指标如表3 ~表5所示。
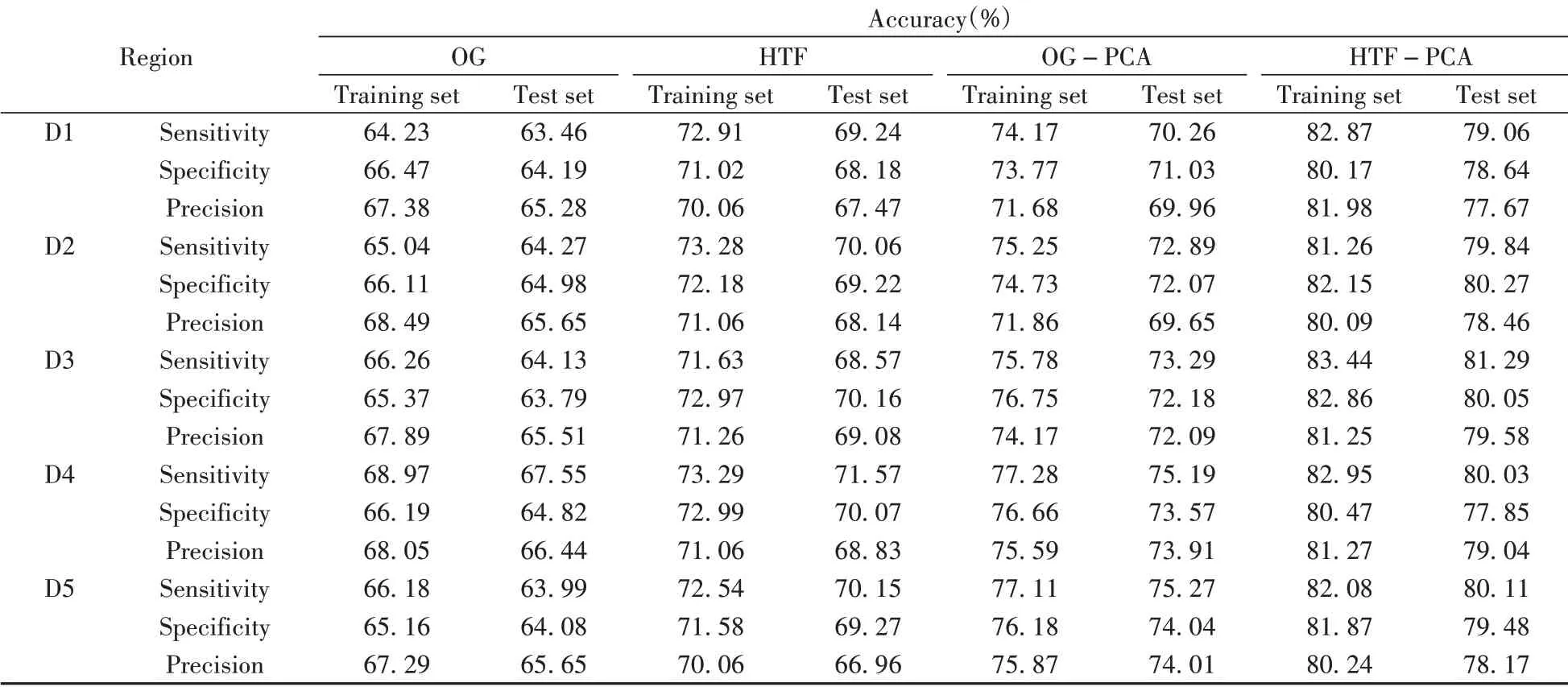
表3 PNB模型的评价指标Table 3 Evaluation index of PNB model
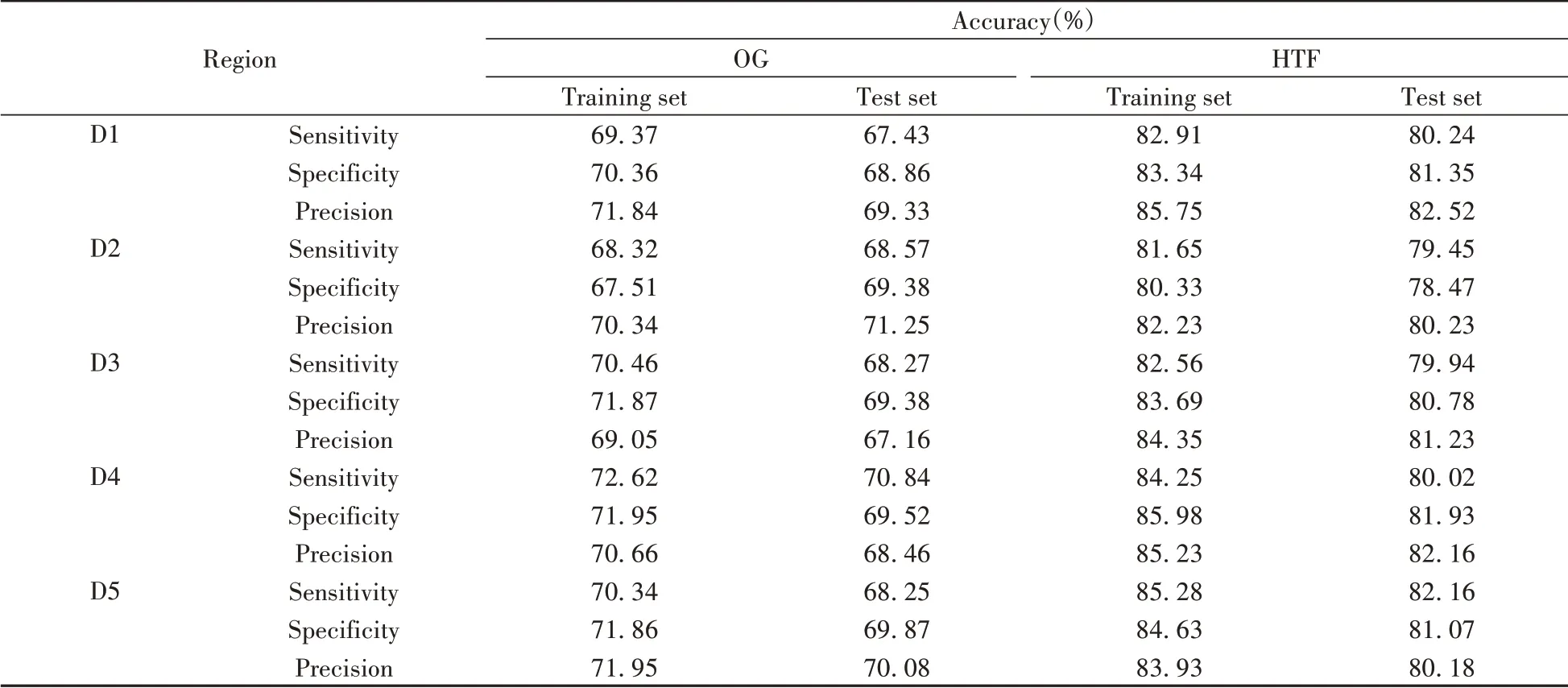
表5 PLS-DA模型的评价指标Table 5 Evaluation index of PLS-DA model
对比表格中3 个模型的评价指标后发现,三者均在经HTF-PCA 处理后达到最优识别效果。对于模型的性能和稳定性,3 个模型的排序为:RF>PLS-DA>PNB,其中RF 模型的平均灵敏度比PLS-DA 模型高8.16%,比PNB模型高10.63%;平均特异性比PLS-DA 模型高8.03%,比PNB 模型高11.56%;平均精度比PLS-DA 模型高7.68%,比PNB模型高11.85%。分析原因可能是PNB模型需要样本数据集之间相互独立,而指甲样本之间可能存在一定的关联性,会使PLS-DA 模型产生过拟合现象,影响模型的准确率。RF 模型采样的随机性则保证了RF 模型不会出现数据过拟合现象,从而使得其识别效果在3个模型中最佳。
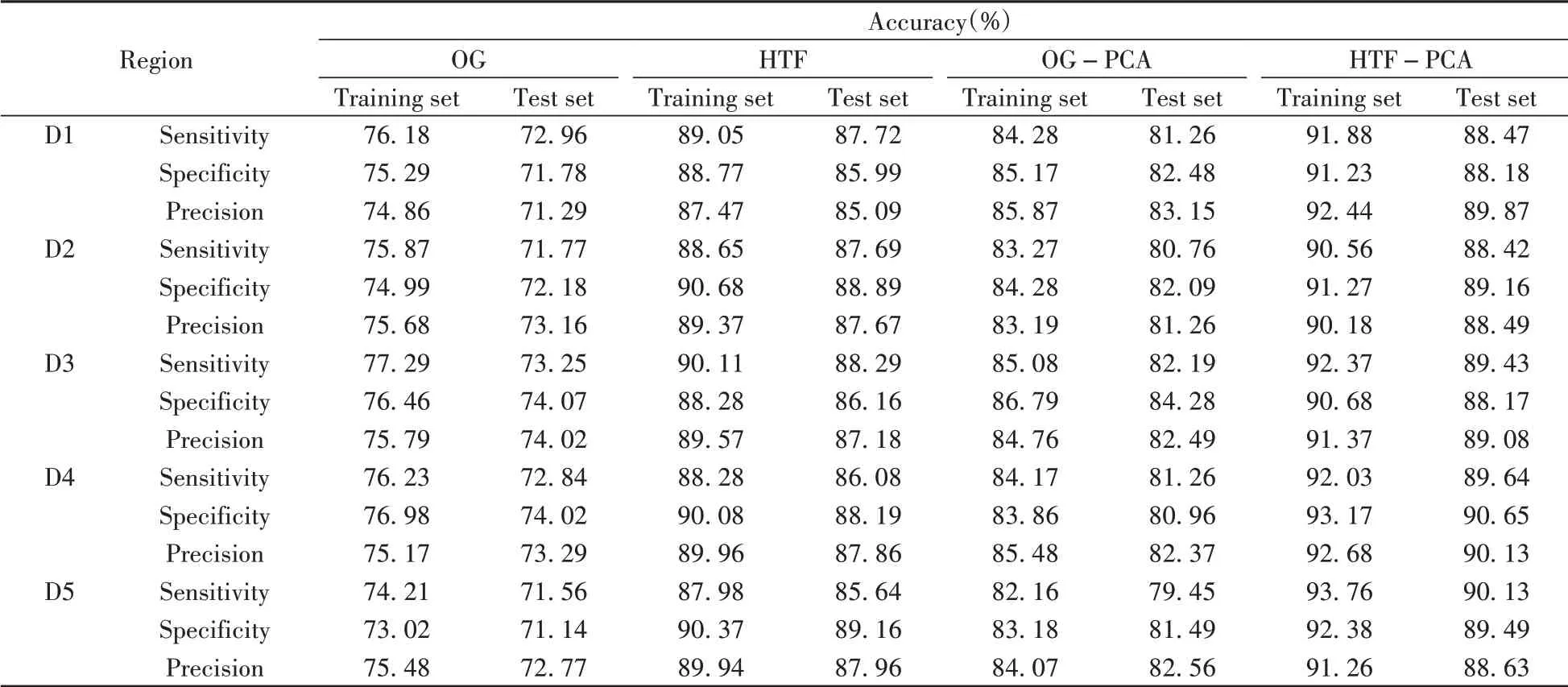
表4 RF模型的评价指标Table 4 Evaluation index of RF model
4 结 论
本实验采集了5 个地区人指甲的红外光谱数据,由于原始谱图的噪声及数据维度较大,因此采用希尔伯特变换滤波器进行降噪处理,同时采用PCA 进行数据降维,利用PNB、RF 及PLS-DA 模型对预处理后的数据进行识别,并根据模型的识别率和相关指标选择最佳预处理方法及最优识别模型。结果表明,预处理方法及模型的筛选降低了谱图的噪声和数据的冗余,同时提高了模型的识别效果,希尔伯特变换滤波器结合PCA 是最佳预处理方法,RF 模型比PNB 模型以及PLS-DA 模型更适合于指甲样本的地区区分。本方法实现了指甲样本地区的无损区分,符合法庭科学对指甲样本的鉴定要求,为法庭科学对指甲样本地区的区分提供了参考。
- 分析测试学报的其它文章
- 地下水中102种酸性、碱性和中性有机污染物的气相色谱-质谱法同时快速测定
- 基于超高效液相色谱-四极杆-静电场轨道阱质谱的结直肠腺瘤患者血清代谢组学研究
- 金-银双金属纳米簇@多壁碳纳米管-二氧化钛纳米材料为新型氧化还原探针构建电化学免疫传感器
- Preparation and Identification of Reference Materials of Isorhamnetin and Rutin in Seabuckthorn Fruit Powder
- 羧基微孔有机网络材料的合成及其对水中苯并三唑类污染物的快速吸附与去除
- 基于激发态分子内质子转移的新型聚集诱导荧光探针用于硫化氢的检测及细胞成像

