大推力液体火箭发动机试验用涡轮流量计结构优化设计

孙鹏飞,徐鸿鹏,李涛,李大海,李宝童,洪军

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安;3.西安航天动力试验技术研究所,710100,西安)

涡轮流量计作为大推力液体火箭发动机燃料供给系统的关键精密测量组件,其测量精度对研制发动机、获取发动机的准确特性具有非常重要的现实意义。作为典型的速度式流量计,涡轮流量计由流体推动涡轮旋转,根据涡轮旋转角速度与流体流速的比例关系,实现对流量的监测。此外,涡轮流量计因具有重复性好、量程范围宽、适应性强、精度高、体积小等特点,被广泛应用于多种领域[1-2]。目前,涡轮流量计的测量性能通常采用水或柴油进行鉴定,而在大推力液体火箭发动机燃料供给系统中,涡轮流量计的工作环境为低温液氧,介质和温度的转变会导致涡轮流量计的测量偏差。

为提升涡轮流量计的测量精度,常见的方法为优化涡轮流量计的几何构型,例如导流架的类型[3-4]、导头形状[5-6]、凹槽宽度[7]、导程长度[8]以及涡轮的构型[9-10]。其中,导流架通过对流体介质的流动方向进行导向,维持了流体介质的稳定运动方向。对具有不同导头的导流架研究结果表明,在大流量条件下,相比于传统球形导流架,流线型导流架因具有更缓的渐变梯度导头,有效降低了涡轮流量计运行管道内的速度梯度,提升了涡轮流量计的测量精度[5]。此外,合理减小导流架的凹槽宽度还能有效降低涡流引起较大的压力损失[7],从而保证了流量计的测量精度。然而,在实际应用中,发动机的供液系统通过测量流量计的涡轮转速,实现对流体介质流量的监测。与导流架相比,优化涡轮构型能进一步有效地提升其测量精度。在涡轮的优化中,通常将涡轮的叶片数、轮毂半径、导程等参数作为优化变量[7,11]。例如,对于小口径涡轮流量计,通过增大涡轮的轮毂半径、轮毂长度和叶片导程,使其仪表系数线性度误差由5.23%降低到4.69%,实现了涡轮流量计测量精度的提升[10]。可以涡轮流量计的涡轮导程、叶片数和前后导流架的轮毂长度为设计变量,在高黏度流体介质下进行响应面和正交试验,得到了具有仪表系数线性度误差最小化的优化变量组合,使仪表系数线性度误差下降了0.12%[12]。综上所述,现有研究对涡轮流量计的优化设计侧重于小口径流量计涡轮的整体构型和导流构件,且关于大口径涡轮流量计的叶片构型对测量精度影响的研究较少。因此,有必要对大口径涡轮流量计展开研究,提升其应用价值。

本文以大推力液体火箭发动机供氧系统中的试验用大口径DN600涡轮流量计为研究对象,采用六自由度(6DOF)模型[13-14]结合流体仿真方法,研究了涡轮流量计在水介质和液氧中的仪表系数等效关系,预估了涡轮流量计在液氧中的测量精度,并以仪表系数线性度误差最小化为优化目标,对涡轮叶片进行优化设计。

1 研究对象及方法

1.1 研究对象

图1为大推力液体火箭发动机供氧系统。其中,Dn为管道的内径尺寸。本文以大推力液体火箭发动机中的DN600涡轮流量计为研究对象,对涡轮叶片构型进行优化,实现对其测量精度的提升。根据涡轮流量计的平面参数化图形,提取其叶片的基本结构参数,如表1所示,并建立涡轮叶片三维结构模型,如图2所示。此外,为便于流量计优化中模型重构参数的选定,将其几何参数保留一位有效位数。

表1 DN600涡轮流量计叶片基本结构参数

叶片的厚度、中径来流角和宽度分别如图3所示,中径来流角为涡轮叶片中间段与流体介质流动方向的夹角。叶片宽度为叶片在x方向的跨度。叶片重合度即n个叶片在zoy平面上的投影面积与涡轮工作平面面积的比例系数。

图1 大推力液体火箭发动机供氧系统Fig.1 The oxygen feeding system of high-thrust liquid rocket engine

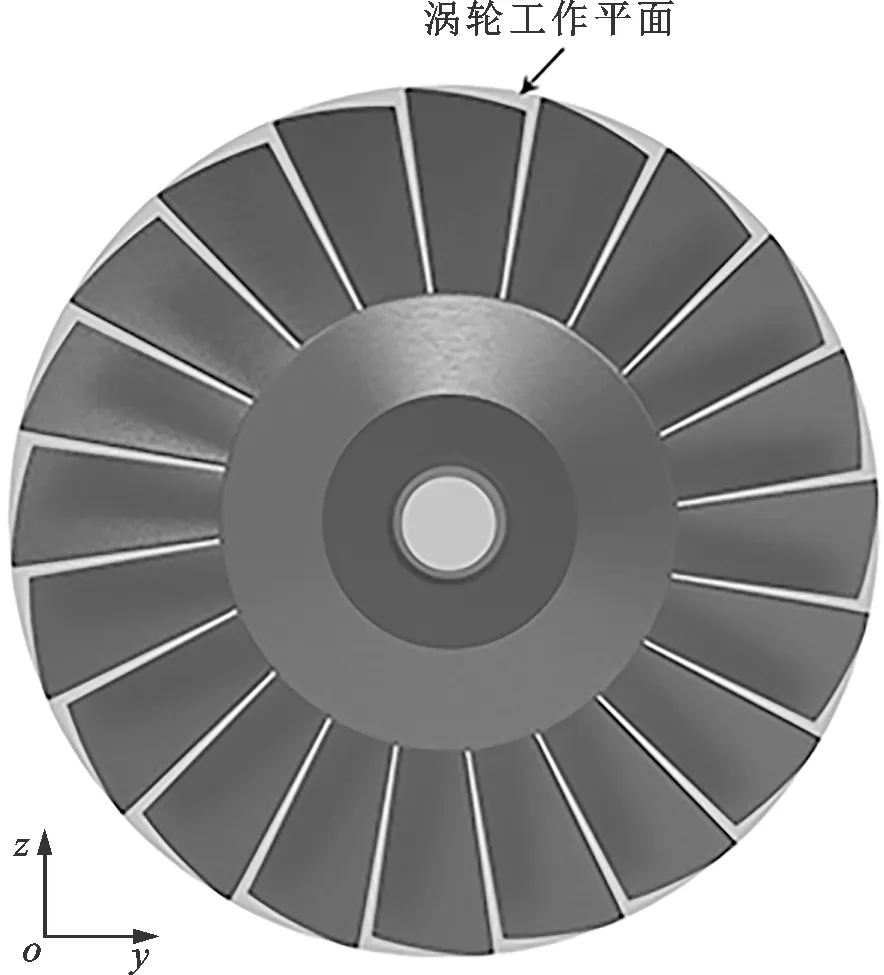
图2 涡轮叶片三维结构模型Fig.2 The three-dimensional model of turbine blades

在叶片优化过程中,为便于获得具有不同构型的叶片,根据其几何参数的耦合关系,建立叶片数n、叶片重合度k、叶根偏角α1、叶顶偏角α2、叶根圆心角θ1、叶顶圆心角θ2、叶根半径Rl、叶顶半径Rt、中径来流角α3和叶片宽度h的函数表征关系,如式(1)～式(4)所示。

叶根偏角α1、叶根圆心角θ1、叶根半径Rl与叶片宽度h的关系为

θ1=2arcsin(htanα1/2Rl)

(1)

叶顶偏角α2、叶顶圆心角θ2、叶顶半径Rt与叶片宽度h的关系为

θ2=2arcsin(htanα2/2Rt)

(2)

(a)叶片厚度 (b)中径来流角 (c)叶片宽度

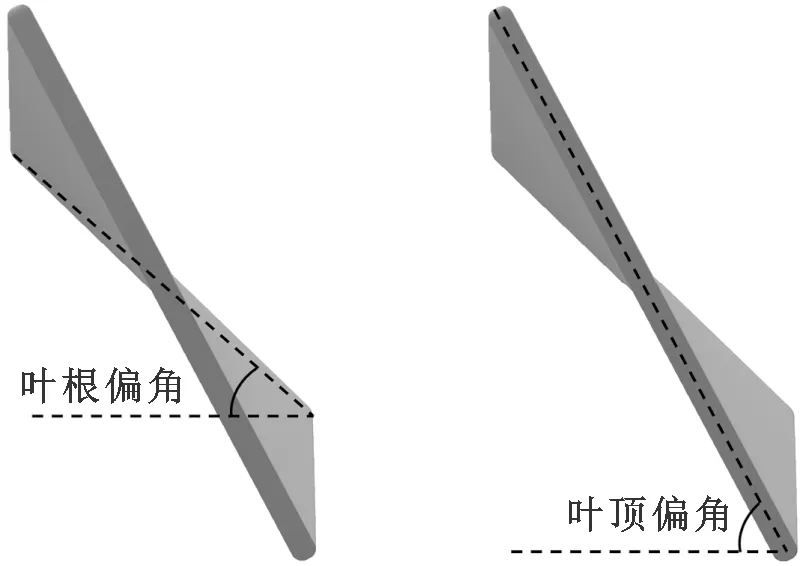
(d)叶根偏角 (e)叶顶偏角图3 涡轮叶片俯视图Fig.3 The top view of turbine blades

叶根偏角α1、叶顶偏角α2与中径来流角α3的关系为

α3=(α1+α2)/2

(3)

叶根圆心角θ1、叶顶圆心角θ2及重合度k的关系为

θ1=θ2=360k/n

(4)

涡轮流量计运行机制为前后导流架固定,涡轮绕中心轴旋转运动,故对仿真流域进行三段式建模,分别为进口上游区域、涡轮区域和出口下游区域,涡轮流量计的局部管道模型如图4所示。DN600涡轮流量计沿x方向的总跨度为811.6 mm,叶顶直径为588.0 mm。

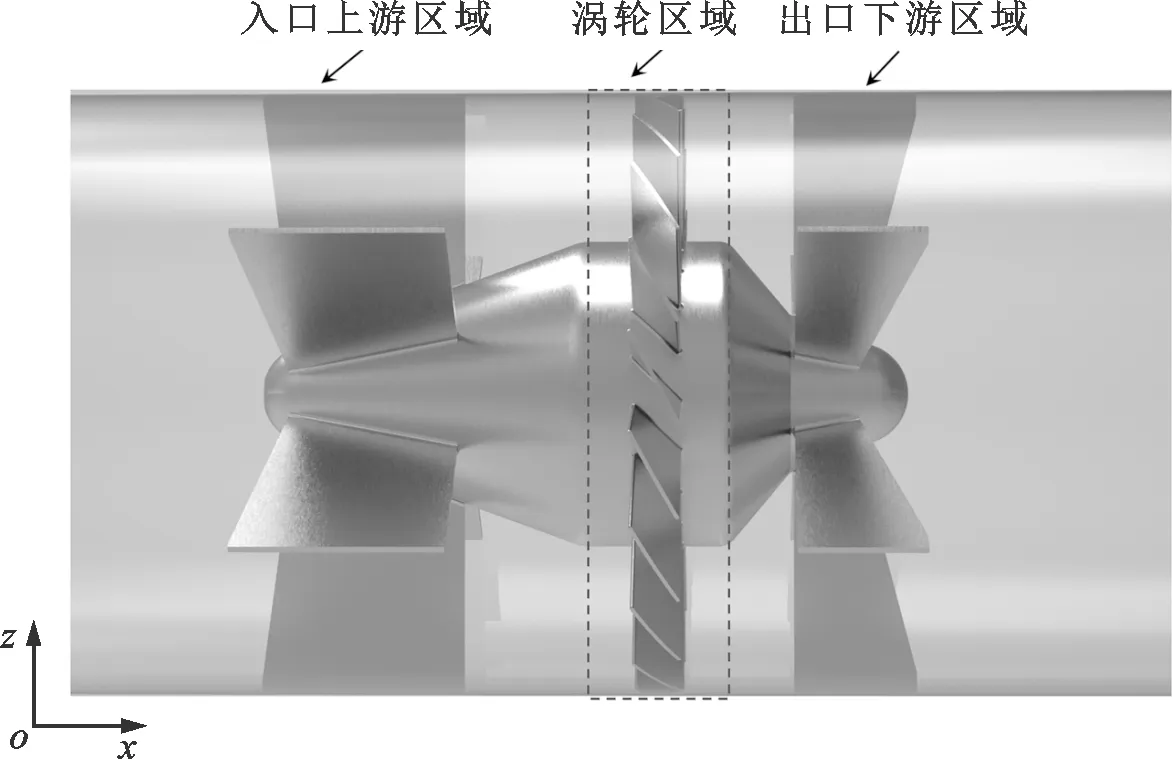
图4 涡轮流量计的局部管道模型Fig.4 The local pipeline model of the turbine flowmeter

1.2 数值模拟方法与矫正

涡轮流量计受到流体冲击时,涡轮在流体驱动力矩作用下被动旋转。因此,为得到不同流量下涡轮流量计的转速,分析其仪表系数线性度误差,本文采用ANSYS/Fluent商业软件,分别对涡轮流量计模型展开定常与非定常分析。由涡轮的运行机制可知,其初速度为0,在定常分析中仅需设定入口流速和出口压强进行仿真计算,在本文中出口均定义为自由出口。在非定常分析时,通过6DOF模型将流量计涡轮区域的运动形式定义为被动,自由度定义为绕x轴的单一转动自由度[14],并将定常分析结果作为初始值进行求解[15-17]。

1.2.1 网格无关性验证

在有限元分析中,不同数量级的网格对物理场结果的影响不可忽视。随着有限元网格数增加,分析结果越精确,但是求解过程也越复杂、计算效率越低。因此,需综合考虑仿真计算精度、计算机的运算能力和工时等多方面因素的影响,选取合适的网格数以保证仿真方法的可靠性和经济性。在水介质条件下,本文分别采用121万、160万、200万、250万和334万5种数量级的网格进行有限元仿真分析。水介质仿真网格无关性验证如图5所示。

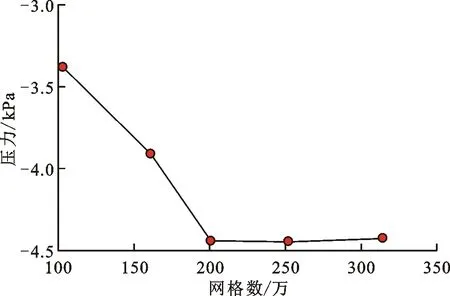
图5 水介质仿真网格无关性验证Fig.5 The mesh independence validation

由图5可知,出口压力随网格数的增加而逐渐上升,当网格数达到250万以后,出口压力趋于稳定,且不断增加网格数对于仿真结果没有实质性的影响,可认为当网格数达到250万以后,仿真结果与网格无关。因此,在水介质条件下,均采用250万数量级的网格划分策略,管道模型的进口上游区域和出口下游区域采用四面体单元的体网格,网格大小为35 mm;涡轮区域采用四面体单元的面网格,网格大小为5 mm;前后导流架的壁面采用四面体单元的面网格,网格大小为7 mm。涡轮流量计的流体域有限元模型如图6所示。

图6 涡轮流量计的流体域有限元模型Fig.6 The fluid-field finite element model of the turbine flowmeter

1.2.2 数值模拟方法的矫正

在运行过程中,涡轮流量计的涡轮因流体驱动力矩Td、流体黏性阻力矩Trf、轴承摩擦机械阻力矩Tb和电磁阻力矩Tm的作用而发生旋转运动,其转动的微分方程[18]如下式

(5)

式中:J为涡轮的转动惯量;ω为涡轮稳定状态时的转速。

为分析涡轮流量计的力矩,从叶片任意半径r处将涡轮展开成直列叶珊,叶片入口和出口的速度三角形如图7所示。

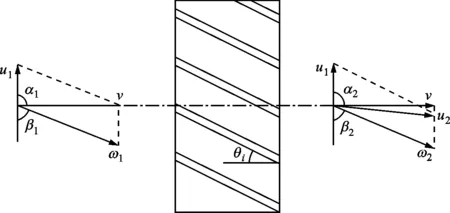
图7 叶片入口和出口的速度三角形Fig.7 The velocity triangle of blades in inlet and outlet

叶片沿高度方向受到的驱动力矩微分方程为

dTd=rdF

(6)

式中:dF为叶片半径r处的驱动力,由动量定理可得知

dF=(vtanθi-rω)2πρvrdr

(7)

式中:v为流体流速;ρ为流体介质密度。tanθi的表达式如下

(8)

由式(8)可得

(9)

从涡轮叶根半径到叶顶半径对式(9)积分得到总驱动力矩,如下式

(10)

(11)

由式(11)可得,涡轮流量计所受到的驱动力矩为

(12)

式中:A为进出口通流面积;Q为流体流量。

本文流体黏性阻力矩分别为涡轮轮毂表面的黏性阻力矩Th、叶片表面黏性阻力矩Ts以及叶顶与管壁间的黏性阻力矩Tt。

根据顺流放置平板表面的阻力研究结果,涡轮轮毂表面的黏性阻力矩[19]为

(13)

Ah=2πRhLh-Ntbhch

(14)

(15)

(16)

式中:Vzh为轮毂位置流体的轴向速度;tbh为轮毂位置叶片厚度;U∞ch为轮毂位置出入口流体的平均相对速度;Rh为轮毂半径;Lh为涡轮的导程;ch为轮毂位置的弦长。本文中Re均表示雷诺数。

叶片表面黏性阻力矩的表达式为

(17)

At=2Nctr

(18)

(19)

(20)

式中ct为叶顶弦长。

根据同轴圆筒壁面间的摩擦力矩,叶顶与管壁间的黏性阻力矩如下

(21)

(22)

式中tbt为叶顶的厚度,本文中即为叶片厚度h。

在实际条件下,转轴与轴承间的油膜不充分导致润滑不足,从而存在机械摩擦阻力矩。在涡轮开始旋转或逐渐停止旋转时,轴与轴承间存在黏性与机械摩擦共存的混合状态,且电磁阻力矩相对较小,对涡轮流量计的影响很小,难以精确获取机械摩擦阻力矩和电磁力矩。因此,本文在6DOF模型中施加预设阻力矩以等效机械阻力矩和电磁阻力矩,对有限元仿真模型进行矫正。

为获得DN600涡轮流量计在不同流量下的仪表系数真实值,在水介质条件下,对不同流量下的DN600涡轮流量计仪表系数分别进行多次试验测量,涡轮流量计试验测量平台如图8所示。通过数值平均得到流量计仪表系数,如表2所示。根据表2中的结果,通过下式分别计算仿真模型在不同流量下的入口流速

(23)

式中R为流体域入口截面半径。

表2 涡轮流量计试验测量数据

根据下式分别计算不同流速的雷诺数[20-21],分析流场的状态

(24)

式中:D为水力直径,对于圆形管道,水力直径即为圆形管道横截面的直径;μ为流体介质的动力黏度。

图8 涡轮流量计试验测量平台Fig.8 The experimental measurement platform of the turbine flowmeter

供氧管道的入口流速和雷诺数如表3所示。由表3可知,所得到的雷诺数的数量级均为106,流场状态可视为湍流状态。此外,根据涡轮流量计的运行机制分析,计算模型可选用标准的k-ε模型[22]。

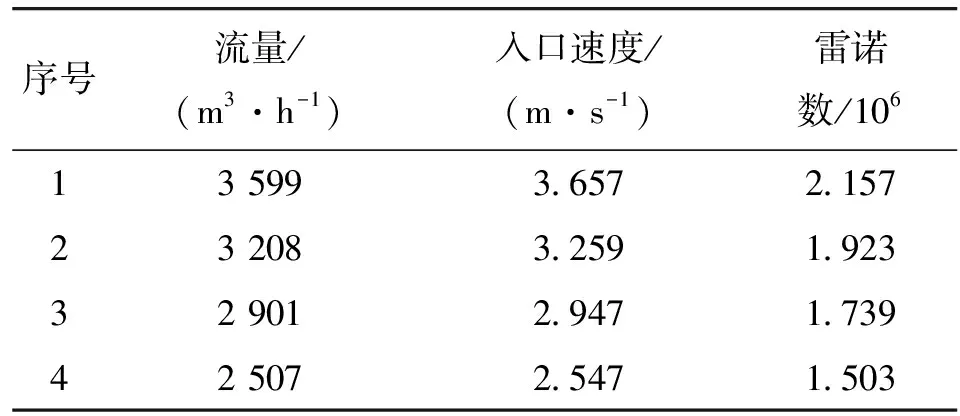
表3 供氧管道的入口流速和雷诺数

根据涡轮稳定状态的转速,可计算得到涡轮旋转频率f,如下式

(25)

基于涡轮旋转频率与流量Q的关系,可得到涡轮流量计仪表系数K,如下式[23]

(26)

根据表3的入口水介质流速条件,对涡轮流量计进行仿真分析,提取涡轮的稳定转速并计算相应的仪表系数。涡轮流量计仿真与试验结果对比如表4所示。

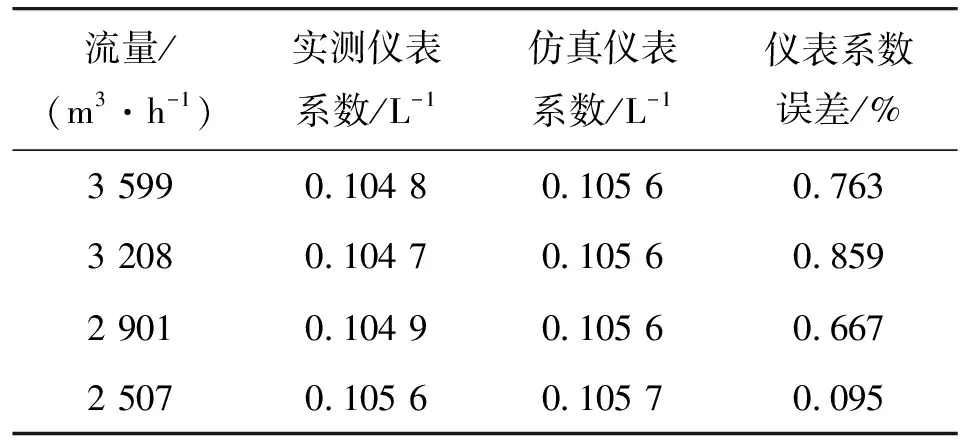
表4 涡轮流量计仿真与试验结果对比

由表4可知,本文所采用的方法与实测数据间的误差均小于0.9%。误差是因为6DOF模型中未考虑摩擦阻力矩和电磁阻力矩的作用。然而,根据实际工程需求,仪表系数误差应不超过0.5%。因此,基于上述数值结果,在6DOF模型中施加预载荷力矩对仿真模型进行误差矫正。通过在不同流量条件下施加多组预载荷力矩进行对比分析,得到如表5所示的矫正结果。

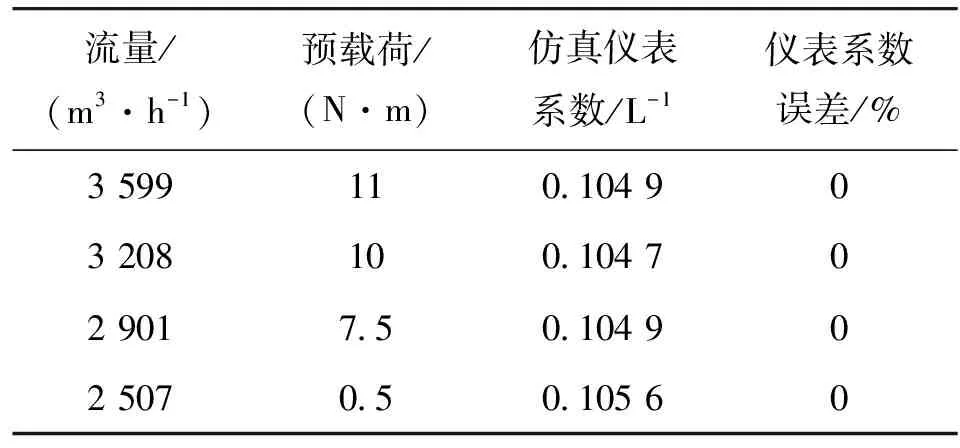
表5 不同流量点下的矫正预载荷力矩

2 水介质和液氧的等效分析

在实际应用中,液体火箭发动机的真实工作环境难以模拟,且采用液氧进行试验以获得涡轮流量计仪表系数的成本高。因此,本文通过数值模拟方法,获得涡轮流量计在水介质和液氧下的仪表系数等效关系,实现对液氧条件下涡轮流量计测量精度的预估。液氧的物性参数如表6所示。

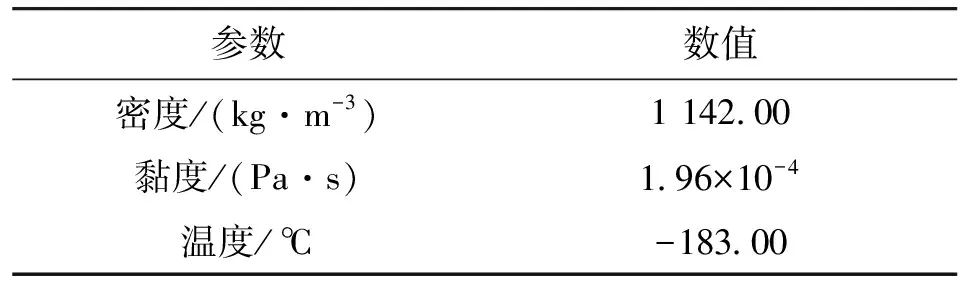
表6 液氧的物性参数

2.1 涡轮流量计热变形分析

由于液氧温度为-183 ℃,涡轮流量计在液氧中会发生冷缩变形,影响其测量精度,需对涡轮流量计进行热变形分析。因此,本文采用热固耦合的仿真方法揭示涡轮流量计的热变形情况。涡轮流量计有限元模型如图9(a)所示,网格类型为6 mm四面体单元的面网格。涡轮流量计的温度载荷边界和约束边界分别如图9(b)和9(c)所示,在涡轮流量计外表面施加-183 ℃的温度载荷,并固定其中心轴。

涡轮流量计的热应变云图如图10所示。由图10可知,涡轮流量计的最大热变形主要集中在导流架的叶片顶部。

2.2 液氧条件下的仿真分析

(a)涡轮流量计有限元模型

(b)温度载荷边界

(c)约束边界图9 涡轮流量计有限元模型与边界条件Fig.9 The finite element model and boundary conditions of the turbine flowmeter

图10 涡轮流量计的热应变云图Fig.10 The total thermal deformation of the turbine flowmeter

首先提取热变形模型的几何信息,对其进行模型重构。然后,在液氧环境下,对重构的涡轮流量计模型进行流场有限元分析,获得涡轮流量计的仪表系数。为保证仿真结果的正确性,分别采用了116万、193万、252万、338万和400万5种数量级的网格进行有限元仿真,分析出口压力的变化以进行液氧仿真网格无关性验证,如图11所示。

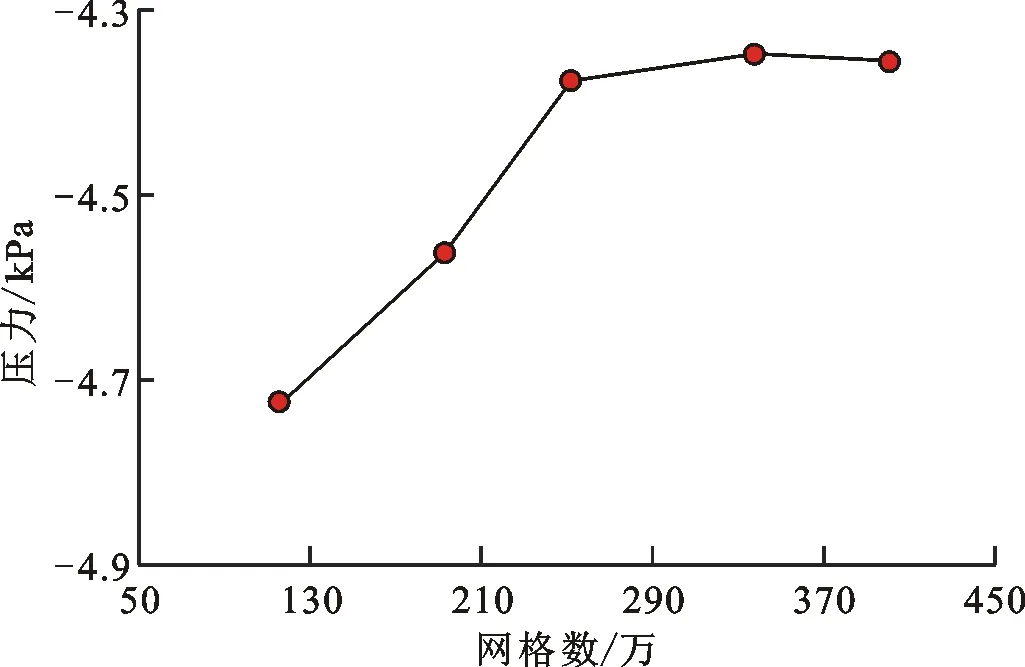
图11 液氧仿真网格无关性验证Fig.11 The mesh independent validation

由图11可知,当网格数达到338万时,出口压力趋于稳定,且不断增加网格数对于仿真结果没有实质性的影响,可认为当网格数达到338万后,仿真结果与网格无关,满足网格无关性的要求。因此,采用338万数量级的网格划分策略,分别在流量为3 599、3 208、2 901和2 507 m3/h的液氧环境下进行仿真分析,获取相应的仪表系数。在338万的网格划分策略中,管道模型的入口上游区域和出口下游区域采用27 mm四面体单元的体网格;涡轮区域采用5 mm四面体单元的面网格;前后导流架的壁面采用5 mm四面体单元的面网格。涡轮流量计在液氧与水介质条件下的仪表系数如图12所示。由图12可知,在液氧和水介质环境下,DN600涡轮流量计的仪表系数成正相关,比例系数近似为0.999 5。

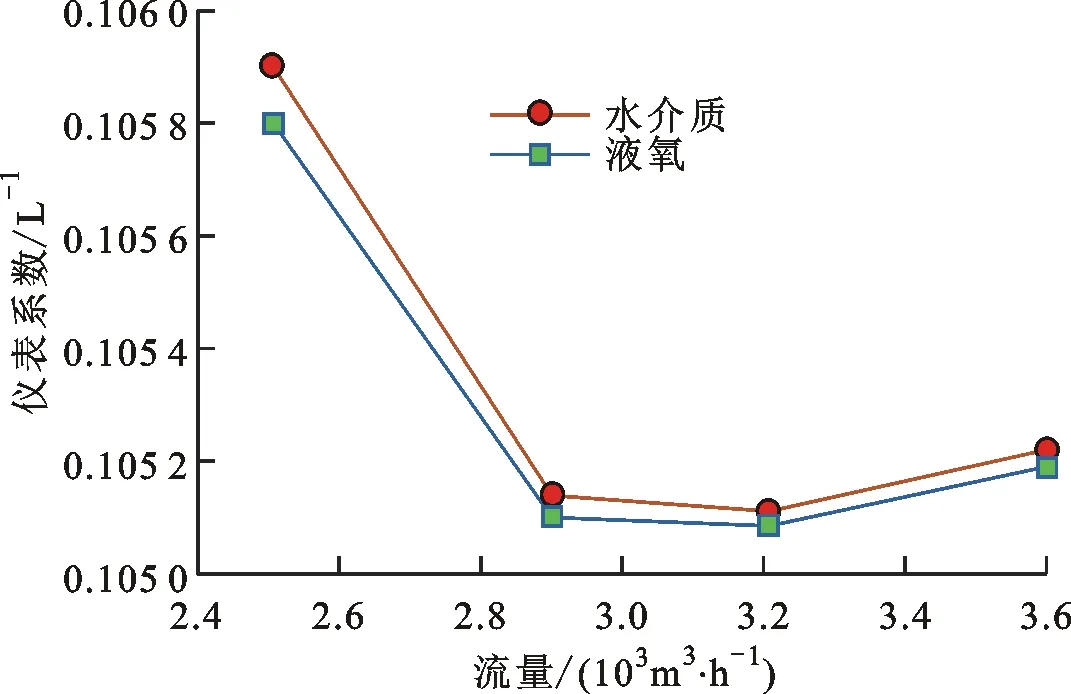
图12 水介质和液氧介质仿真仪表系数Fig.12 The meter coefficient in water and liquid oxygen simulations

3 涡轮流量计叶片优化

为提高涡轮流量计的测量精度,对涡轮叶片的中径来流角、叶片宽度和叶片重合度进行优化。根据实际工程经验,优化参数取值的最大变化范围为30%,且相较于原始构型,优化的叶片构型变化不宜过大。因此,本文分别取中径来流角为45°、50°和55°,叶片宽度为45 mm、55 mm和65 mm,重合度为0.9、1.0和1.1。通过正交试验,分别使用α3、h、k表示中径来流角、叶片宽度和重合度3个因素,如表7所示[24]。每个因素有3个水平,分别为1、2、3。选用L9(34)正交表安排试验,如表8所示。

表7 涡轮叶片参数的因素水平表

由图1可知,在涡轮流量计的真实管道模型中,存在的偏心流会影响流量计的测量精度。因此,为避免因偏心流对优化结果的影响,在仿真过程中采用直管道进行有限元仿真分析,将图4中的入口上游区域定义为10.5Dn,出口下游区域定义为10.5Dn。

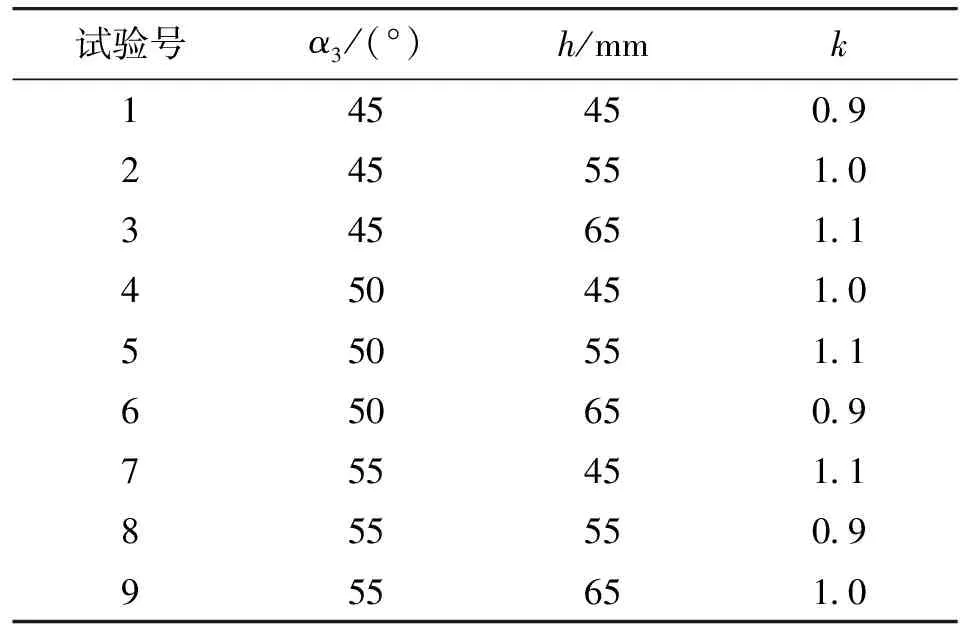
表8 涡轮流量计正交试验表

本文采用仪表系数线性度误差以评估涡轮流量计的测量精度,如下式[25]

(27)

式中:Kmax,i为涡轮流量计在不同流量下得到的仪表系数最大值;Kmin,i为涡轮流量计在不同流量下得到的仪表系数最小值。

涡轮流量计正交试验结果与均值如表9和表10所示。由表10可知,α3对应的第3水平均值最小,表明α3取第3水平上的值时线性度误差最小,同理可以得到h和k的取值均为第2水平。根据涡轮流量计在液氧和水介质中的仪表系数比例关系可知,理论上在液氧环境中的最优水平组合为(α3)3h2k2,即中径来流角、叶片宽度和重合度的优化组合为55°、55 mm、1。

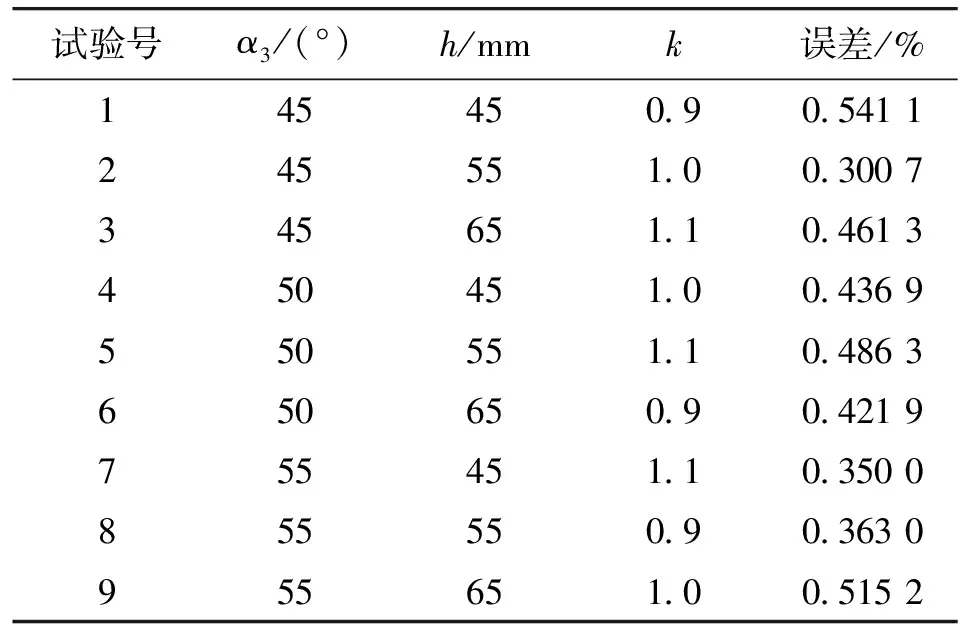
表9 涡轮流量计正交试验结果

表10 涡轮流量计的线性度误差均值

为对比优化前后涡轮流量计的测量精度,分别对优化所得的涡轮流量计进行有限元分析,得到不同流量下的仪表系数,如图13所示。根据图13中结果计算相应的仪表系数线性度误差,结果表明,优化的涡轮流量计仪表系数线性度误差为0.277 0%,相比于原始结构的0.381 5%,降低了0.104 5%,显著提升了涡轮流量计的测量精度。

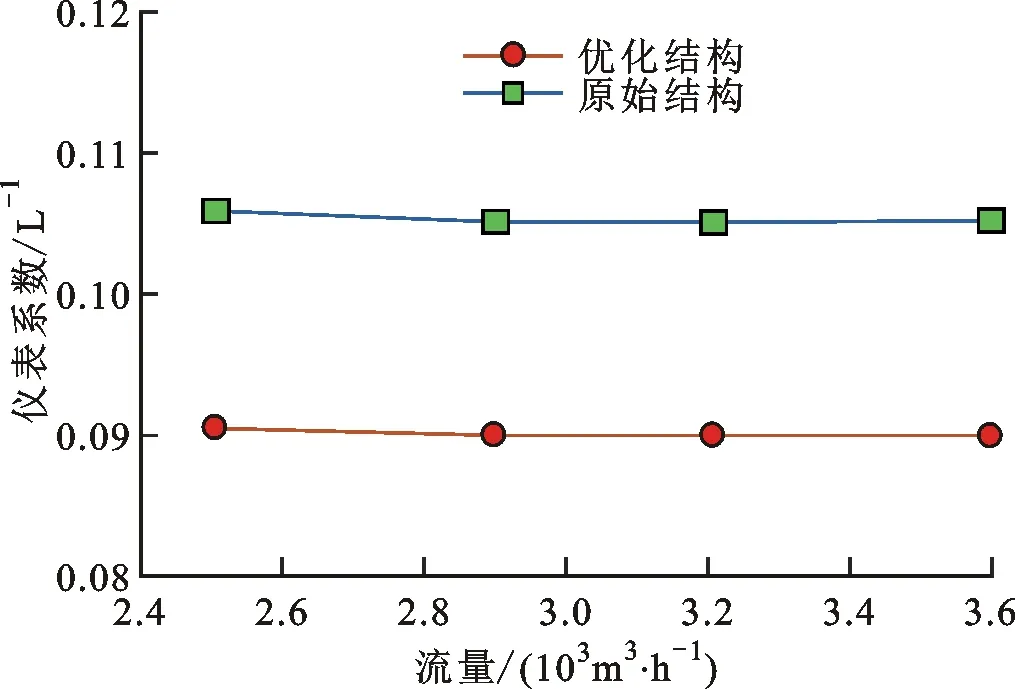
图13 优化前后不同流量下的仪表系数对比Fig.13 The comparison of the initial and optimized meter coefficients

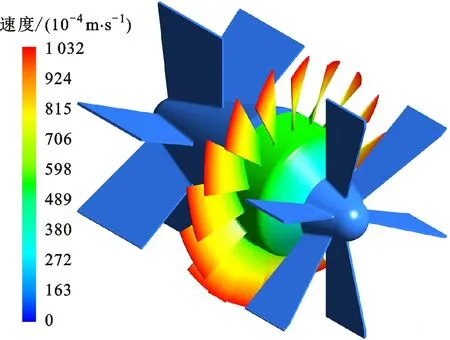
(a)优化涡轮

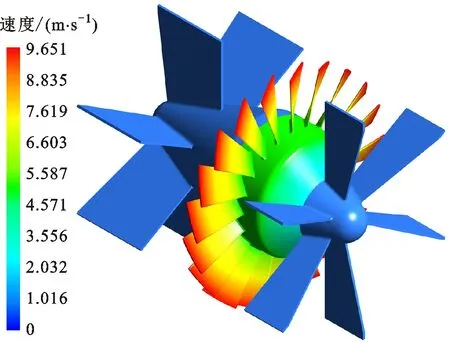
(b)原始涡轮图14 涡轮速度分布云图Fig.14 The velocity distribution of the turbine

为进一步揭示优化后涡轮流量计的测量精度,优化前后涡轮流量计在3 599 m3/h流量下的涡轮速度分布和流场截面速度分布云图分别如图14和15所示。由图14可知,涡轮的最大转速在叶片顶部,相对于原始涡轮流量计,优化的涡轮流量计的转速更大,运转更加顺畅。由图15可知,流体在流经优化的涡轮叶片时,流场速度分布较原始流量计更加均匀。综上所述,优化的流量计涡轮结构在流场中的旋转稳定性更好,从而使测量精度得到提高。

(a)优化结构

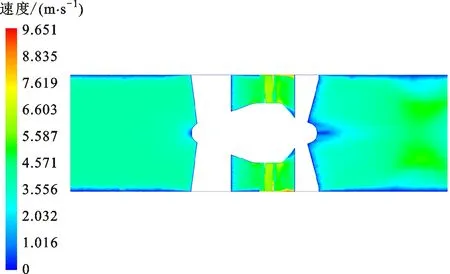
(b)原始结构图15 流场截面速度分布云图Fig.15 The velocity distribution of the flow field

4 结 论

本文以大推力液体火箭发动机供氧系统中的试验用DN600涡轮流量计为研究对象,通过数值模拟获得了涡轮流量计在水介质和液氧环境中仪表系数的等效关系。以仪表系数线性度误差最小为优化目标,通过正交仿真试验优化了涡轮流量计叶片,主要结论如下。

(1)数值仿真结果表明,涡轮流量计在水介质和液氧环境下的仪表系数呈正相关,为液氧流量计的仪表系数修正提供了数据参考。

(2)涡轮流量计中径来流角、叶片宽度和重合度的优化组合为55°、55 mm、1;相比于原始构型,优化的DN600涡轮流量计的线性度误差降低了0.104 5%,测量精度显著提升。