结合信号谐波特性的均值参数测量窗设计

周期信号(实际中为周期和幅度均随时间变化的准周期信号)是人类活动中广为应用的一类信号,如电网电压与电流信号,广播、通信和雷达等各类无线电设备发射的电波信号,引擎与马达发出的振动信号等等。周期信号参数的实时、准确测量是电子测量的基本内容,是设备工作状态分析与故障诊断的重要依据。均值参数是一类重要参数,其计算的核心环节为求信号的均值,如周期信号的有效值、功率及功率的导出参数等均属于周期信号的均值参数

。基于信号采样法对周期信号均值参数的测量主要有同步采样法

和非同步采样法

。本文研究非同步采样法,通过加窗函数的优化设计实现非同步测量误差的有效抑制。均值参数非同步采样测量的主要步骤为信号的周期预估、采样、截取与加窗求均值。由于采样周期只能取整数个时钟周期,因而信号的截取和采样均与信号周期不同步,这将导致均值参数的测量误差。为了方便,在频域中对周期信号均值参数的测量误差进行分析。信号在时域中的加窗和非同步采样,在频域中分别表现为频谱泄漏和栅栏效应

,二者均会导致谐波测量误差。为了抑制加窗引起的频谱泄漏,人们针对不同应用背景和需求下的信号分析构建了一系列窗函数

。为了抑制非同步采样引起的栅栏效应,采用了多谱线插值

以及构造平顶窗

等多种方法。信号均值在频域中对应直流分量,而直流分量的频域采样不存在栅栏效应,对其测量误差的分析只需考虑基波和各次谐波在直流分量处的泄漏干扰。研究发现对信号多次平均可有效抑制非同步采样法的均值测量误差,且多次平均与矩形卷积窗加权等价

。仿真表明相对于其他同宽的窗函数,基于矩形卷积窗对周期信号进行加权时基波和各次谐波在直流分量处的泄漏很小,特别适用于周期信号均值类参数的测量,但矩形卷积窗的最优性尚待研究。

信号分析中的各种加窗函数均可视为不同窗系数加权的组合余弦窗

。传统的窗函数在设计时并没有结合信号频谱的特性,主要基于窗函数频谱的最大旁瓣峰值最小和远程衰减快等约束条件建立窗系数方程组

。本文针对周期信号均值参数的测量,基于窗函数的组合余弦模型并结合周期信号频谱的谐波结构特性,研究组合余弦窗满足的有效条件及构建时的优化准则,建立并求解窗系数方程组进而完成窗函数的设计。另外,对基于矩形卷积窗均值测量的最优性进行了理论分析。

1 组合余弦窗加权测量分析

1.1 周期信号的均值类参数

计算周期信号均值参数时的均值项通常不是原周期信号的均值,而是运算过程中某一周期相同的中间信号的均值

。均值参数计算的关键是算出中间信号的均值,如计算交流电压有效值的关键就是计算交流电压的平方信号(中间信号)的均值。设中间信号用

(

)表示,其周期为

,则均值

可表示为在整数个周期(

)内信号的平均

由于房地产市场火爆异常，各方面的资金、技术力量都潮水般地涌向房地产市场，使住宅工程质量在一定程度上得到提高，但现阶段仍存在许多质量通病问题，其中最直观也是引起群众集中上访投诉最多的主要是“漏、裂、渗、壳、锈”五大类，包含屋面、卫生间漏水；墙体开裂、渗水；墙面抹灰空鼓、不平整，阴阳角不垂直；扶手、栏杆锈蚀等多种问题。

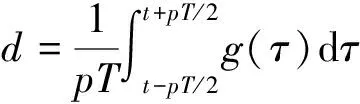
(1)

实际中由于信号的截取和采样与信号周期不同步,计算时只能用预估周期

替代式中的实际周期

,得到均值的近似值

进一步分析矩形卷积窗的傅里叶变换在周期信号预估谐波频点的平坦性,

(

)的1阶导数为

(2)

该均值测量是时间的函数,称为均值测量信号。

采区2号专用回风巷布置在本采区最东面(图1)，主要用于76采区的回风等，巷道埋深560～580 m，沿3号煤层顶板掘进。3号煤层，平均厚6.27 m，以亮煤为主，暗煤次之，加少量丝炭条带；直接顶为泥岩、页岩，平均厚1.29 m，灰黑色，具光滑面，见植物化石；基本顶为细、中粒砂岩，平均厚7.10 m，深灰色，硅质胶结，矿物成分以石英为主，云母次之、含长石；直接底为泥岩、砂质页岩，平均厚0.61 m，深灰色，质均，含云母；基本底为中粒石英砂岩，平均厚3.38 m，灰黑色、中厚层状、含云母，水平纹理发育，上部为角砾结构。

1.2 组合余弦窗及其有效条件

(2)组合余弦窗中谐波次数为

的整数倍的窗系数为0,即

(3)

(

)通常为偶函数。不失一般性,将窗函数表示为由直流分量和

个余弦分量组成的组合余弦窗的形式

,即

按实验方法，绘制试剂空白和钛显色溶液在不同波长下测定的吸收光谱。由图1可见，在阿拉伯树胶溶液存在下，于稀硫酸中，钛与百里香酚蓝形成了蓝紫色络合物，络合物/试剂空白的最大吸收峰位于590nm处，试剂空白/水最大吸收峰位于440nm处，对比度为150nm，说明络合物与显色剂之间的颜色差异大。实验选择590nm作为测量波长。

针对综合课程设计教学过程中出现的上述问题，笔者认为，综合课程设计教学中应充分体现 “以学生为中心”的教学模式，在具体实施过程中采用任务型教学法和讨论法相结合的教学方法，探索实践环节过程管理与考核结果并重的综合成绩评定方法，充分调动学生的积极性、能动性和团队合作精神，重视学生工程实践能力和团队合作能力的培养。

(4)

其中

(

)为归一化矩形函数

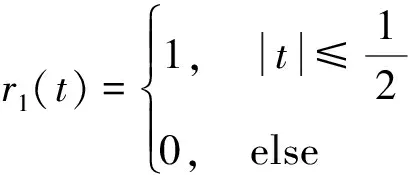
(5)

为组合余弦窗的系数。

取式(4)的傅里叶变换,组合余弦窗的频谱为

(6)

一个组合余弦窗的具体形式决定于窗宽

、余弦分量的个数

以及各窗系数

的取值。为了分析组合余弦窗用于周期信号均值测量的有效性,首先分析均值测量无误差时组合余弦窗须满足的有效条件。

将信号

(

)展开为有限项正弦级数

1)建立并求解了压缩过程的控制方程，结果表明对于等截面的柱形液压缸，活塞质量、液压缸截面积、液压缸长度是影响载荷脉宽的主要因素，通过减小活塞质量、增大液压缸截面积及减小液压缸长度可以减小载荷脉宽。

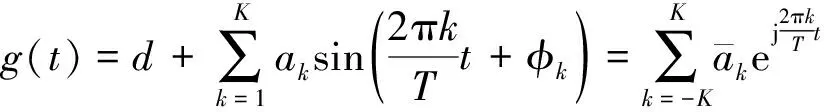
(7)

其傅里叶变换为

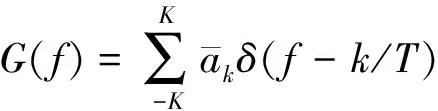
(8)

实际上式(3)给出的均值测量信号恰好是

(

)与

(

)的卷积,故均值测量信号的频谱为

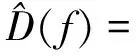
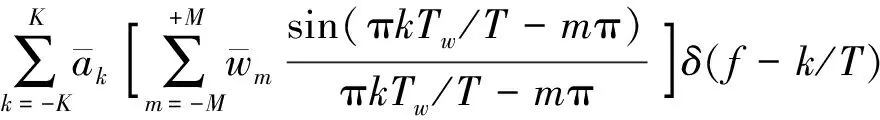
(9)

均值测量的误差决定于均值测量信号中的交流分量,即

≠0的各次谐波分量。假设均值测量信号中的各次谐波能够完全得以抑制,且直流分量与被测信号的直流分量相等,对上式进行分析可得到用于均值测量的组合余弦窗的有效条件。

根据频域采样定理,宽度为

的

重矩形卷积窗在频域可以通过频率采样间隔为Δ

=1

的频域采样进行重建

=

=1,2,3,…

(10)

这一条件表明,窗函数频谱在信号各次谐波频点的值为0。

计算均值的更一般的表示形式为基于宽度为

的窗函数

(

)对信号加权

=0

mod

=0且

≠0

(11)

这一条件表明,组合余弦窗中不含与信号谐波同频的余弦分量。

(3)组合余弦窗为单位面积的窗函数,即

(12)

该条件可使均值测量信号的直流分量与中间信号的直流分量相等。

以上为组合余弦窗的有效条件。只有组合余弦窗满足以上3个条件,才能准确算出周期信号的均值。

1.3 均值参数测量的误差分析

实际中在构建组合余弦窗时,只能用信号的预估周期

替代信号的实际周期

,因而组合余弦窗的有效条件表现为

=

、

=1以及不含与预估谐波频率(

)相同的余弦分量。在式(4)中引入有效组合余弦窗条件,得

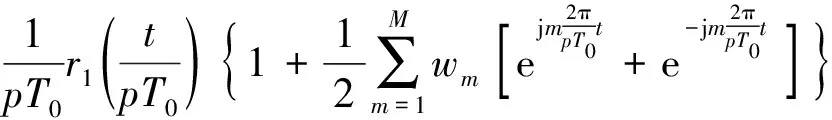
(13)

其傅里叶变换为

模拟得到圆柱壳、开孔圆柱壳、含补强件圆柱壳的轴向压力与轴向位移变化关系如图9所示，轴压曲线先增大后减小。轴压峰值分别为195.4 MPa、158.4 MPa、164.8 MPa。

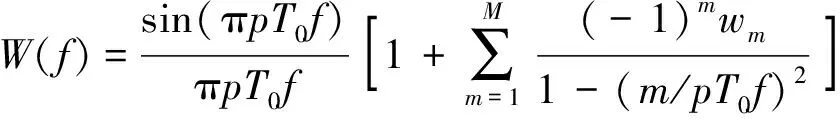
(14)

在一般情况下预估周期

虽然不等于信号周期

,但二者非常接近。为了定量分析因信号的截取和采样与信号周期不同步带来的均值测量误差,引入相对频偏

=(

-

)

=(

-

)

(15)

该式中

和

分别为周期信号的实际频率和预估频率。再利用信号第

次谐波的频率

=

,则均值测量信号的频域表示式(9)可写为

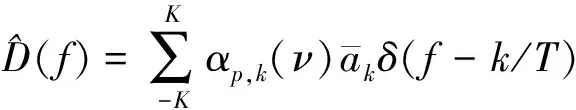
(16)

函数在一点平坦意味着函数在该点的邻域内为频偏的高阶无穷小量。无穷小量的阶数可用于函数平坦性度量,阶数越高则函数在该点的平坦性越好,因此窗宽为

个周期的窗函数的优化设计准则可描述为

,

(

)=

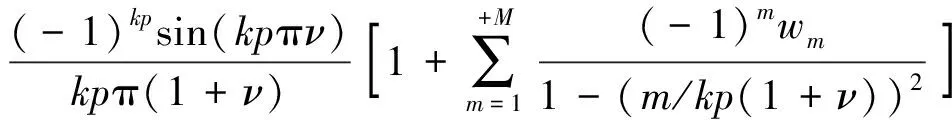
(17)

对式(16)进行傅里叶反变换,均值测量的时域形式为

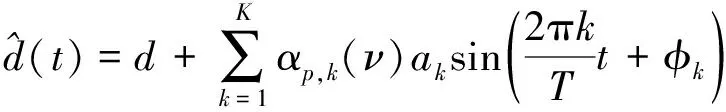
(18)

式中右边第二项为

时刻的测量误差。用均值测量信号随时间变化的标准差表示均值参数的测量误差,再利用各次谐波之间的正交性可得测量误差为

(19)

2 窗函数的优化设计

满足均值测量有效条件的组合余弦窗可使相对频偏为0时的均值测量误差为0,但实际中相对频偏不为0,因而均值测量误差也不为0。组合余弦窗的设计就是在误差最小的原则下确定组合余弦窗的系数,为此需首先给出组合余弦窗的优化准则及其相应的数学表示。在进行一般信号的频谱分析时,文献中通常以窗函数频谱的旁瓣峰值最小以及旁瓣的远程衰减最快作为优化准则,这在一般意义上可以最大限度地抑制各频谱分量之间的相互泄漏,但若用于周期信号均值参数测量,组合余弦窗的优化准则尚待研究。

周期信号的主要结构特点是谐波性,其频谱为分布于各谐波频点(

=

)上的离散谱。实际中的非同步采样虽然存在相对频偏,但预估周期非常接近信号的实际周期,周期信号的各次谐波频率只在以各次谐波预估频率(

)为中心的邻域内变化。为了有效抑制周期信号的均值测量误差,在以各次谐波预估频率为中心的邻域内均值测量信号的频谱幅值越小越好,这等同于组合余弦窗在满足均值测量有效条件的基础上其频谱在各次谐波预估频点满足平坦性。可见,在进行周期信号均值参数测量时,所选的加窗函数的频谱只需在各次谐波预估频点的邻域内最小,而不必关心在其他频域处的取值。综上所述,面向周期信号均值测量的组合余弦窗的优化准则为:窗函数的频谱在信号谐波频点的值为0且满足平坦性。

其中

,

为信号第

次谐波的衰减因子

一个晶体,往往不是一次长成，在不同生长阶段,介质环境可能会出现某些显著差异,特别是铁、钛、钒离子等致色元素的含量变化,致使同一晶体不同阶段形成的各部份之间的颜色差异,并在晶体中留下每一阶段生长的痕迹,这就是色带。

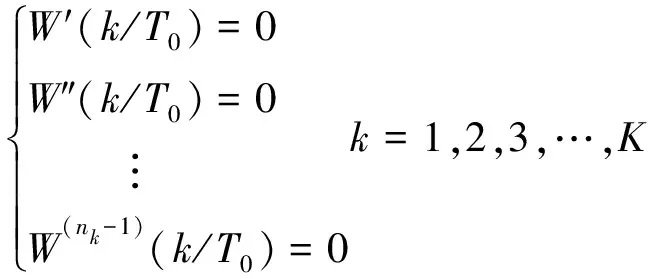
(20)

如果上式成立,则在以

次谐波频点为中心的邻域内组合余弦窗的频谱

(

)为频偏的

阶无穷小量。

将式(14)代入式(20)给出窗系数

的方程组,其中

(

)在

次谐波频点的1～3阶导数为0对应的系数方程分别为

(21)

(22)

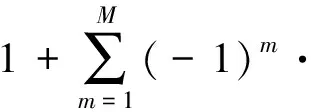
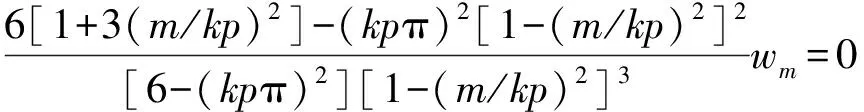
(23)

进一步还可以导出4阶以上导数为0对应的窗系数方程,这里从略。

设信号含有

个谐波,组合余弦窗的宽度为

个信号预估周期,则待确定的

(

-1)个窗系数为

,

,…,

-1

,

+1

,

+2

,…,

2-1

,

2+1

,…,

+1

,

+2

,…,

-1

。根据组合余弦窗应满足的有效条件2,与信号谐波同频的余弦分量对应的窗系数须为0。窗系数方程的个数应该与待定的窗系数的个数相等。一般情况下,在建立窗系数方程时,一方面要提高

(

)在各信号谐波频点连续导数为0的阶数,一方面又要求

(

)在这些频点有相同的平坦性。为此,由

(

)在各信号谐波频点的前(

-1)阶导数为0列出

-1个方程,

个谐波频点共列出

(

-1)个方程。

对只有部分谐波分量不为0的周期信号,列方程时不必要求

(

)在所有预估谐波频点具有相同的平坦性。这种情况下,通常在信号能量较强的频点赋予较高的平坦性,在信号能量很弱或不存在的频点赋予较低的平坦性或完全不予置理。较多的窗系数意味着组合余弦窗中有更多的余弦分量可用于调控预估谐波频点的频谱平坦性,但往往以增大各预估谐波频点之间的频谱为代价,一旦信号有谐波落入这些区域就会带来较大误差。较少的窗系数虽然只能使较少预估谐波频点处的频谱平坦性得到控制,但其他频域处的频谱往往可以维持在较低的幅度,即便信号有谐波落入这些区域也能得到有效抑制。事实上,由于平坦性约束条件可以进行多种组合,适用于任一周期信号均值参数测量的最佳窗函数并不存在。实际中组合余弦窗的窗宽和窗系数的选择应根据具体信号的谐波分布特点进行优化设计。

在精彩的歌舞表演中，颁奖典礼高潮迭起。在众人期待中，主持人正式公布本届金樽奖金樽大奖及金奖名单，晚宴嘉宾为获得金樽大奖的5款葡萄酒，获得金樽奖金奖的19款葡萄酒颁奖、合影留念，并颁出“金樽奖微醺大师”等单项奖。

3 矩形卷积窗性能分析

矩形卷积窗用于周期信号均值参数测量时可以有效抑制非同步采样带来的测量误差,而且算法简单高效

。本节基于组合余弦窗的有效条件和优化设计准则对矩形卷积窗的性能进行分析。

板涧河调蓄水库主要建筑物，包括大坝、溢洪道、导流泄洪洞、连通洞及补水泵站。大坝为2级建筑物，溢洪道和泄洪洞为3级建筑物，补水泵站为2级建筑物。洪水标准为50年一遇设计，1 000年一遇校核。

3.1 矩形卷积窗的时域表示

对式(5)给出的归一化矩形窗进行多重卷积,得归一化

重矩形卷积窗

(24)

更一般情况,借助宽度为1个信号预估周期

的矩形窗

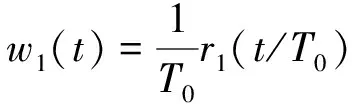
(25)

定义一般情况下的

重矩形卷积窗为

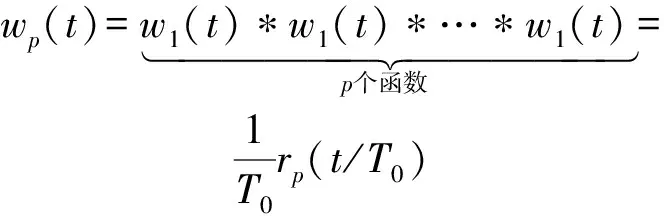
(26)

它是一个

周期宽、单位面积的偶函数。

3.2 矩形卷积窗的频域表示

根据卷积定理,式(26)给出的矩形卷积窗的频域表示为

(27)

(1)组合余弦窗的窗宽为信号周期的整数倍,即

(

)=

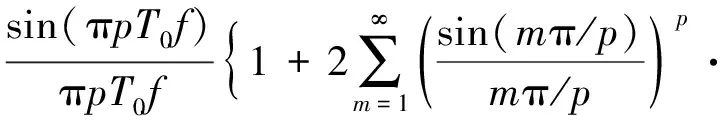
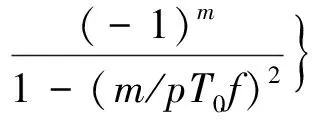
(28)

与式(14)对照可知,如果将矩形卷积窗理解为组合余弦窗的一种,则其对应的组合余弦窗系数为

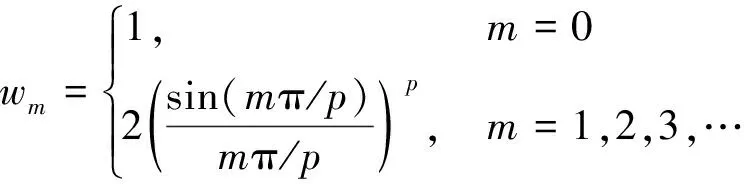
(29)

由式(28)可知在诸谐波频点上,矩形卷积窗的频谱为0;由式(29)可知矩形卷积窗对应的组合余弦窗系数

为1,且不存在与信号谐波同频的余弦分量(

为

的整数倍时

=0),因此矩形卷积窗为满足均值测量有效条件的组合余弦窗。

斜杠人生的雏形就是我们平时所说的兴趣爱好。一个人有什么爱好，就用斜杠表述。比如俺老彭爱写稿、爱打羽毛球、爱养兰花。三者呈并列关系，用斜杠隔开，便是：写稿/打羽毛球/养兰花。不过，“不是所有牛奶都叫特某苏”，也不是所有带斜杠的东西都叫“斜杠人生”。

1.2.6 Transwell实验检测过表达miR-454-3p对SW480细胞侵袭能力的影响 将以无血清细胞培养液稀释的Matrigel基质胶包被transwell小室基底膜的上室表面,加入100 μL无血清培养基稀释的各组细胞悬液,在小室下层孔板中加入含10%血清的完全培养液，置于37℃孵箱培养培养24 h后取出培养小室的,湿棉签轻轻拭去上层小室内的基质胶和细胞，4%多聚甲醛固定后行结晶紫染色，晾干后，显微镜下选5个视野计数穿出细胞数目。

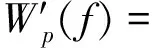
(π

)

-(-1)

sin

-1

(π

)cos(π

)

-

-

故{An(xk)}是([0,1], ρ)的Cauchy-列。由题设条件知([0,1], ρ)完备,从而{An(xk)}是([0,1], ρ)的收敛列。设

(π

)

-

sin

(π

)

-(+1)

(30)

进一步还可求出各高阶导数,不难看出

(

)的第1至

-1阶导数的各求和项中均含有sin(π

)的幂。频率

为1

的整数倍时sin(π

)=0,因而矩形卷积窗的频谱在各信号谐波频点的1～

-1阶导数均为0。这表明2重以上矩形卷积窗的

(

)在信号的各预估谐波频点均满足平坦性(至少为1阶导数为0),当频偏趋于0时,周期信号的均值测量误差为相对频偏的

阶无穷小量。

矩形卷积窗为含有无限个余弦分量的组合余弦窗,基于矩形卷积窗的均值测量信号的傅里叶变换仍由式(16)给出,

次谐波的衰减因子为

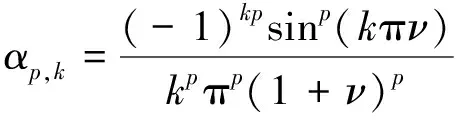
(31)

均值测量的标准差由式(18)给出,相对频偏趋于0时的近似为

图3为模拟后不同压下量下的等效应变分布云图，从图3(a)可以发现，在第30步时，上下端面位置应变较大，心部最小，在试样鼓肚位置应力均匀分布。图3(b)中的应变分布有所增加，其最小和最大应变值均有所提高。在图3(c)中，试样中应变分布与图3(b)相似，应变值进一步增加。

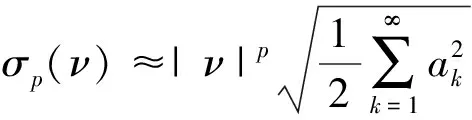
(32)

4 优化组合余弦窗应用举例

实际信号可能只包含有限次的谐波分量,且信号能量在各次谐波上的分布极不平衡,如电力信号主要由奇次谐波组成。交流电有效值计算中的中间信号为交流电的平方信号,主要由偶次谐波组成。作为实例,基于优化组合余弦窗对交流电有效值的测量进行数值仿真。设被测交流电信号含有5项奇次谐波,即

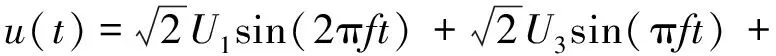
(33)

其中各谐波的有效值

=1、

=0.356 236 9、

=0.213 742 1、

=0.152 673 0、

=0.118 745 6,该交流电压信号的总有效值

=1.1。有效值对应交流电的均方根,计算中的中间信号为

(

)=

(

),显然该信号仅含有最高谐波次数为18的偶次谐波。

信号

(

)的有效值的加窗测量过程为,首先用窗函数对中间信号

(

)加权求其均值,然后再计算平方根。由于

(

)仅含偶次谐波,并考虑到随着谐波次数的提高其在直流分量处的泄漏干扰逐渐消弱,以下以窗函数的频谱

(

)在谐波次数为2、4、6、8、10的频点处平坦作为构建组合余弦窗的优化条件。在该5个谐波频点上,通过使

′(

)=

″(

)=0构建2周期窗宽的优化组合余弦窗WCOS2,通过使

′(

)=

″(

)=

‴(

)=0构建3周期窗宽的优化组合余弦窗WCOS3。表1给出了方程(21)(22)(23)解得的窗系数。

在已有的窗函数中,矩形卷积窗用于周期信号均值参数测量时的非同步误差最小,故只需将优化组合余弦窗与同宽的矩形卷积窗进行对比分析。图1、图2分别给出了2周期窗宽的优化组合余弦窗WCOS2、矩形卷积窗WCON2与3周期窗宽的优化组合余弦窗WCOS3、矩形卷积窗WCON3的幅度谱。可以看出,在选定的偶次谐波频点处优化余弦组合窗的频谱(实线)明显较矩形卷积窗的频谱(虚线)平坦。

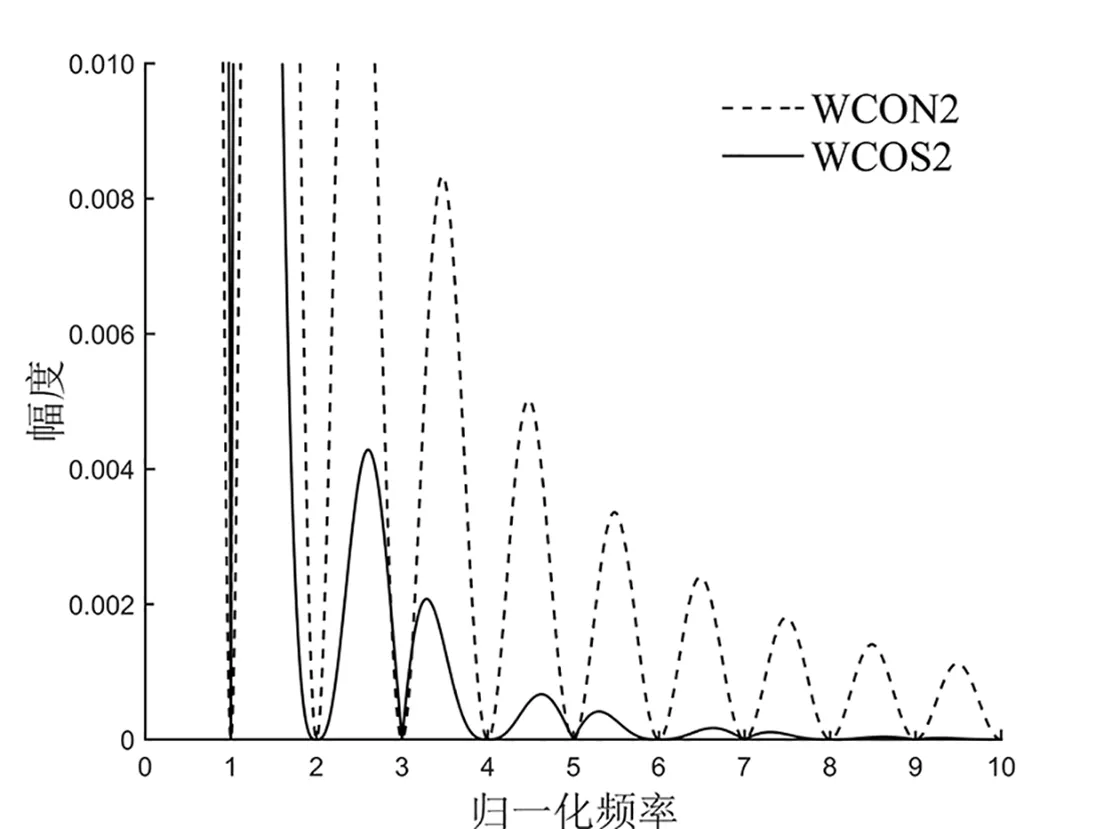
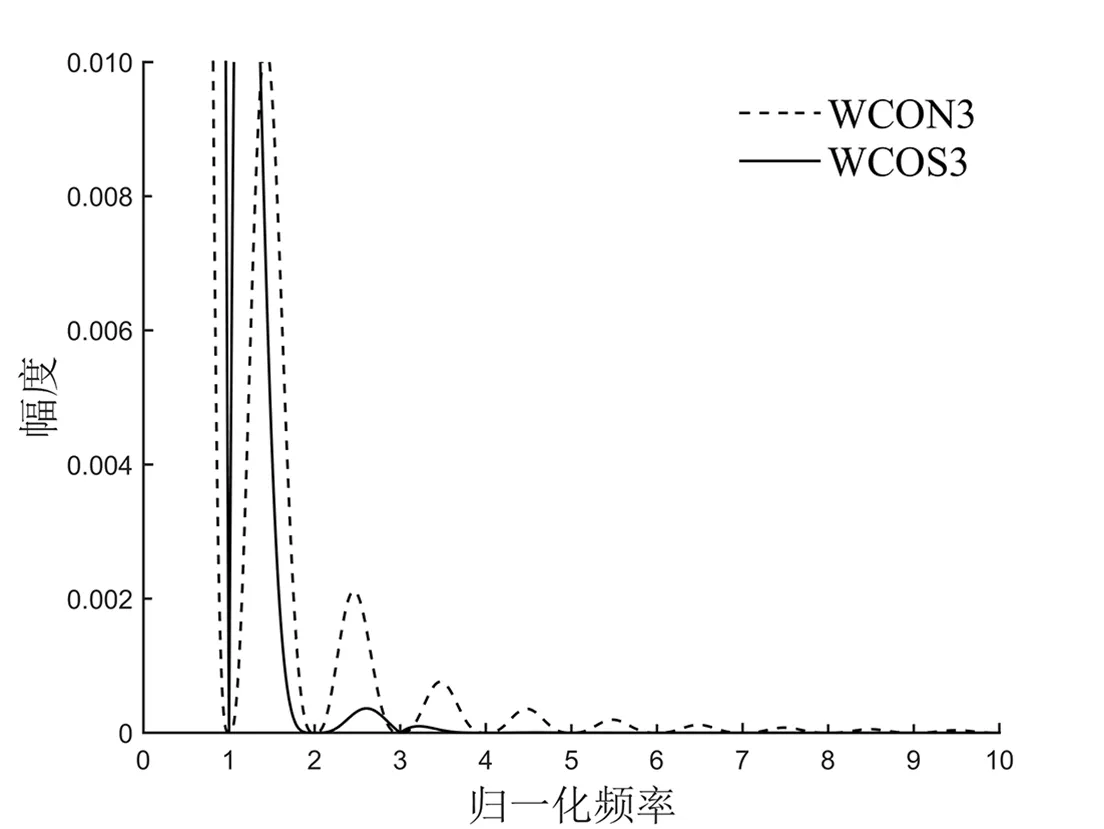
仿真中一个预估周期内对信号采样100次,信号相对频偏

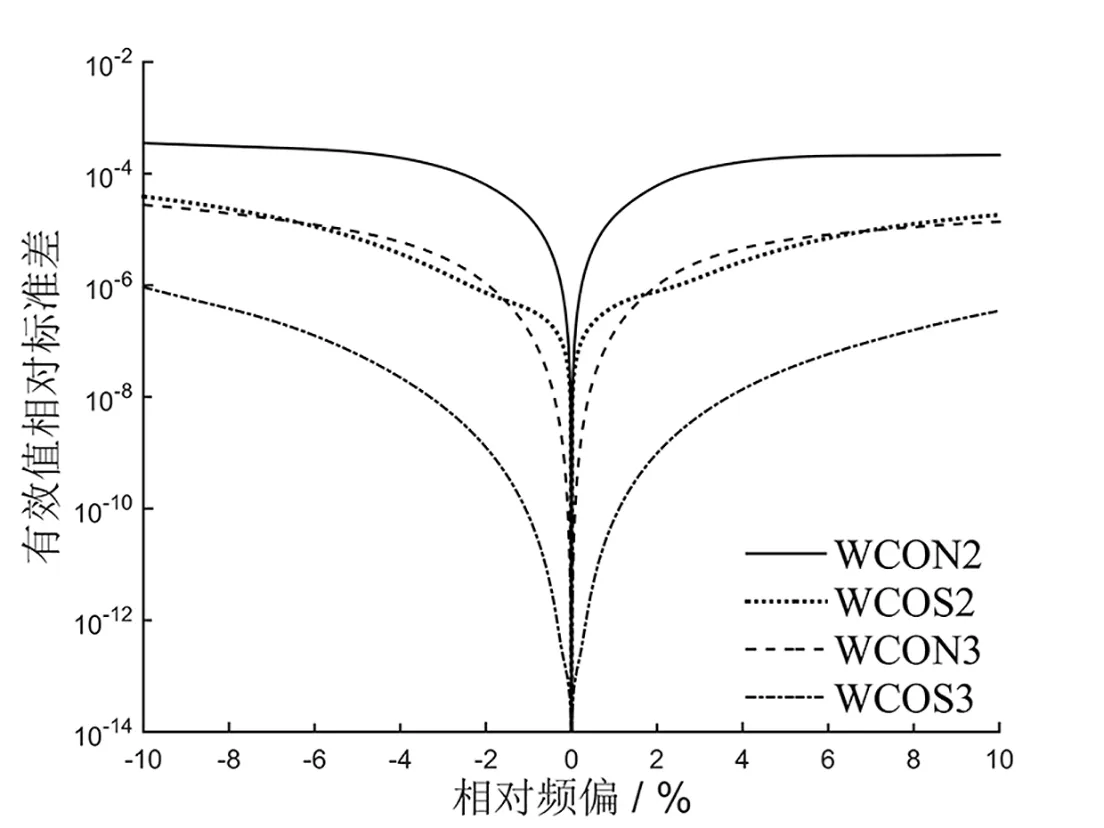
的变化范围为-10%～10%。图3为相对频偏变化时,优化组合余弦窗WCOS2、WCOS3和矩形卷积窗WCON2、WCON3用于有效值测量时的测量误差。比较WCOS2(点线)、WCON2(实线)、WCOS3(点划线)、WCON3(虚线)可知,与同宽的矩形卷积窗相比,采用窗宽为2个和3个信号周期的优化组合余弦窗后测量精度分别提高了11倍和27.5倍以上;3周期窗宽的优化组合余弦窗的测量精度高出2周期窗宽的优化组合余弦窗40倍以上。另外,在整个±10%的频偏范围内,WCOS2和WCON3的测量精度大致相近,这是因为二者的频谱

(

)在信号主要谐波(2、4、6、8、10次谐波)处均有

′(

)=

″(

)=0,但当频偏较小(±1.6%之内)时,WCOS2明显低于WCON3的测量精度。实际上用于均值测量的中间信号

(

)还含有12、14、16、18次谐波分量,但由于WCOS2的频谱在这些频点并未用

′(

)=

″(

)=0加以约束,频偏很小时这些高次谐波分量在直流分量(均值)处的干扰逐渐显露。

通过对只有奇次谐波的交流电有效值进行仿真计算表明,信号频率在较大范围(±10%)变化时,WCOS2和WCON3对应的有效值测量的相对标准差分别小于10

和10

,这说明实际中只需2个或3个信号周期的采样数据即可实现高精度测量。

5 结 论

采样不同步是影响周期信号均值类参数测量精度的主要因素,对信号加窗能够有效抑制不同步误差。论文基于组合余弦窗并结合周期信号的谐波特性进行研究,导出了信号频率变化时均值参数测量的误差公式;基于频偏为0时的测量误差为0,给出了组合余弦窗的有效条件:窗宽为信号周期的整数倍、所含余弦分量不能与信号谐波同频以及窗函数的面积为1;提出了组合余弦窗的优化准则:窗函数的频谱在信号谐波频点应满足平坦性,也即在这些频点上窗函数频谱的1阶导数为0或连续有多阶导数为0;基于优化设计准则建立了组合余弦窗的系数方程组,实现了适于周期信号均值测量的组合余弦窗优化设计;基于组合余弦窗分析了广泛用于周期信号分析的矩形卷积窗,导出了矩形卷积窗对应的组合余弦窗系数,说明了信号各谐波同等地位时矩形卷积窗的最优性。最后,基于优化组合余弦窗对测试信号进行了数值模拟,结果表明信号频率在较大范围(±10%)变化时,基于优化组合余弦窗的测量精度显著高于同宽的矩形卷积窗的测量精度。

:

[1] 戴先中. 准同步采样及其在非正弦功率测量中的应用 [J]. 仪器仪表学报, 1984, 5(4): 309-396.

DAI Xianzhong. The quasisynchronous sampling and its application in the measurement of nonsinusoidal power [J]. Chinese Journal of Scientific Instrument, 1984, 5(4): 309-396.

[2] 温和, 滕召胜, 曾博, 等. 基于三角自卷积窗的介损角测量算法及应用 [J]. 电工技术学报, 2010, 25(7): 192-198.

WEN He, TENG Zhaosheng, ZENG Bo, et al. Dielectric loss angle measurement algorithm and application based on triangular self-convolution window [J]. Transactions of China Electrotechnical Society, 2010, 25(7): 192-198.

[3] 万全, 高云鹏, 罗志坤, 等. 基于Nuttall窗频谱校正的介质损耗因数测量 [J]. 仪器仪表学报, 2010, 31(1): 15-20.

WAN Quan, GAO Yunpeng, LUO Zhikun, et al. Dielectric loss factor measurement based on Nuttall window spectral correction [J]. Chinese Journal of Scientific Instrument, 2010, 31(1): 15-20.

[4] 孟卓, 温和, 李华, 等. 电压不平衡度的准同步采样快速测量方法 [J]. 仪器仪表学报, 2015, 36(3): 574-583.

MENG Zhuo, WEN He, LI Hua, et al. Fast measurement method for voltage unbalance factor based on quasi-synchronous sampling algorithm [J]. Chinese Journal of Scientific Instrument, 2015, 36(3): 574-583.

[5] FLORES-ARIAS J M, ORTIZ-LOPEZ M, QUILES LATORRE F J, et al. A memory-efficient true-RMS estimator in a limited-resources hardware [J]. Energies, 2019, 12(9): 1699.

[6] TYAGI T, PARASURAMAN S. Finer granularity DFT bins with moving window for capacitance sensing [J]. IEEE Transactions on Industrial Informatics, 2021, 17(1): 504-513.

[7] FERRERO A, OTTOBONI R. A low-cost frequency multiplier for synchronous sampling of periodic signals [J]. IEEE Transactions on Instrumentation and Measurement, 1992, 41(2): 203-207.

[8] KOLANKO J K. Accurate measurement of power, energy, and true RMS voltage using synchronous counting [J]. IEEE Transactions on Instrumentation and Measurement, 1993, 42(3): 752-754.

[9] DAI Xianzhong, GRETSCH R. Quasi-synchronous sampling algorithm and its applications [J]. IEEE Transactions on Instrumentation and Measurement, 1994, 43(2): 204-209.

[10]NUTTALL A. Some windows with very good sidelobe behavior [J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(1): 84-91.

[11]SHUAI Zhikang, ZHANG Junhao, TANG Lu, et al. Frequency shifting and filtering algorithm for power system harmonic estimation [J]. IEEE Transactions on Industrial Informatics, 2019, 15(3): 1554-1565.

[12]ZHANG Jieqiu, LIANG Changhong, CHEN Yanpu. A new family of windows: convolution windows and their applications [J]. Science in China: Series E Engineering & Materials Science, 2005, 48(4): 468-481.

[13]陈砚圃, 张介秋. 周期信号均值型参数的矩形卷积窗加权测量 [J]. 探测与控制学报, 2020, 42(3): 51-56.

CHEN Yanpu, ZHANG Jieqiu. Measurement and analysis of periodic signal parameters based on rectangular convolution window weighting [J]. Journal of Detection & Control, 2020, 42(3): 51-56.

[14]谢航, 廖与禾, 林京. 一种含噪声多模态调频调幅信号的提取方法 [J]. 西安交通大学学报, 2012, 46(7): 93-97.

XIE Hang, LIAO Yuhe, LIN Jing. Amplitude modulation-frequency modulation multi-mode noise signal extraction by short-time Fourier transform [J]. Journal of Xi’an Jiaotong University, 2012, 46(7): 93-97.

[15]KITZIG J P, BUMILLER G. Fast-Decaying sine ramp windows for signals with limited frequency resolution [J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-13.

[16]REDDY M V, SODHI R. An open-loop fundamental and harmonic phasor estimator for Single-Phase voltage signals [J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4535-4546.

[17]WU Minshun, LIU Zhiqiang. Noncoherency correction algorithm for removing spectral leakage in ADC spectral test [J]. IEICE Electronics Express, 2016, 13(2): 20150991.

[18]付江铎, 伍民顺, 班诚, 等. 应用于高精度ADC频谱测试的改进加窗技术 [J]. 电子测量与仪器学报, 2020, 34(5): 9-15.

FU Jiangduo, WU Minshun, BAN Cheng, et al. Improved windowing applied to high-precision ADC spectral test [J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(5): 9-15.

[19]刘冬梅, 杨重良, 何怡刚, 等. 基于Rife-Vincent自卷积窗三谱线插值FFT电力谐波分析 [J]. 电子测量与仪器学报, 2016, 30(9): 1351-1360.

LIU Dongmei, YANG Chongliang, HE Yigang, et al. Harmonic analysis of power system based on Rife-Vincent self-convolution window triple-spectral-line interpolation FFT [J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(9): 1351-1360.

[20]刁瑞朋, 孟庆丰. 一种衰减信号加窗频域插值算法 [J]. 西安交通大学学报, 2013, 47(7): 85-90.

DIAO Ruipeng, MENG Qingfeng. Interpolation algorithm for discrete Fourier transforms of weighted damped sinusoidal signals [J]. Journal of Xi’an Jiaotong University, 2013, 47(7): 85-90.

[21]WEN He, LI Chengcheng, TANG Lu. Novel three-point interpolation DFT method for frequency measurement of sine-wave [J]. IEEE Transactions on Industrial Informatics, 2017, 13(5): 2333-2338.

[22]BORKOWSKI J, MROCZKA J, MATUSIAK A, et al. Frequency estimation in interpolated discrete Fourier transform with generalized maximum sidelobe decay windows for the control of power [J]. IEEE Transactions on Industrial Informatics, 2021, 17(3): 1614-1624.

[23]张强, 王海云, 王维庆. 一种新型组合优化谐波分析方法研究 [J]. 电力系统保护与控制, 2020, 48(10): 156-163.

ZHANG Qiang, WANG Haiyun, WANG Weiqing. A new combined optimization harmonic analysis method [J]. Power System Protection and Control, 2020, 48(10): 156-163.

[24]SALVATORE L, TROTTA A. Flat-top windows for PWM waveform processing via DFT [J]. IEE Proceedings: B Electric Power Applications, 1988, 135(6): 346-361.

[25]RELJIN I S, RELJIN B D, PAPIC V D. Extremely flat-top windows for harmonic analysis [J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(3): 1025-1041.