Smart grid dispatch powered by deep learning:a survey*

Gang HUANG ,Fei WU ,Chuangxin GUO

1Zhejiang Lab,Hangzhou 311121,China

2College of Computer Science and Technology,Zhejiang University,Hangzhou 310027,China

3College of Electrical Engineering,Zhejiang University,Hangzhou 310027,China

E-mail:huanggang@zju.edu.cn;wufei@zju.edu.cn;guochuangxin@zju.edu.cn

Abstract: Power dispatch is a core problem for smart grid operations.It aims to provide optimal operating points within a transmission network while power demands are changing over space and time.This function needs to be run every few minutes throughout the day;thus,a fast,accurate solution is of vital importance.However,due to the complexity of the problem,reliable and computationally efficient solutions are still under development.This issue will become more urgent and complicated as the integration of intermittent renewable energies increases and the severity of uncertain disasters gets worse.With the recent success of artificial intelligence in various industries,deep learning becomes a promising direction for power engineering as well,and the research community begins to rethink the problem of power dispatch.This paper reviews the recent progress in smart grid dispatch from a deep learning perspective.Through this paper,we hope to advance not only the development of smart grids but also the ecosystem of artificial intelligence.

Key words: Artificial intelligence;Deep learning;Power dispatch;Smart grid

1 Introduction

Power systems can be traced back to the Pearl Street station and its distribution network built by Thomas Edison (Kundur,1994).They were first built to support lighting systems only,but soon spread to provide energy for many other applications with the accelerated adoption of electrification technologies (Mai et al.,2018).This revolution is still ongoing.For example,we see more and more electric vehicles running on the road in daily life.In fact,a reliable supply of electricity has already become a cornerstone of our digital economy (Walsh,2013),and it is of vital importance in many areas,including transportation(Jaller et al.,2020),finance(Oughton et al.,2017),food and agriculture (Zimmerman R et al.,2016),and epidemic prevention and control (Liu ZF,2020).Its increasing importance indicates increasing complexities,and smart grids are believed to be the next-generation power system(Gharavi and Ghafurian,2011;Wen GH et al.,2021)for meeting the increasing requirements.

Smart grid will be much more complicated than traditional power systems.It is essentially an electrical grid enhanced by information technology (Hossain et al.,2012),which turns the electrical grid into an intelligent system.The features of smart grids and conventional power grids are summarized in Table 1.The main benefits of smart grids include the following:(1) efficiency-smart grids enable greater utilization of generators and lines;(2) resiliencesmart grids ensure a more reliable supply ofelectricity,especially against disasters; (3)sustainability-smart grids permit greater penetration of renewable energy sources;(4) marketenabling-smart grids allow more choices and therefore lower energy bills.

Power dispatch is a kernel problem that must be addressed in fulfilling the smart grid promise(Gandhi et al.,2016).With the purpose of deciding a best strategy for power generation,transmission,and even consumption,smart grid dispatch connects different components within the whole system.In particular,demand is always changing over space and time,which requires dispatch methods to be reliable and computationally efficient (Hasan et al.,2020).Furthermore,with the increased integration of intermittent renewable energies(Huang et al.,2015;Wen YF et al.,2016)and the severity of uncertain disasters getting worse (Huang et al.,2017a,2017b),the generation and transmission parts of grids are now becoming more and more uncertain,which makes the smart grid dispatch problem even more challenging than ever before.

Artificial intelligence(AI)is now a popular technology in various industries (Wu F et al.,2020).It promises to revolutionize almost all kinds of tough problems by switching the original problem to a data-driven one.This is a new paradigm for scientific research(Hey et al.,2009)and has proved its power and efficiency in many real-world applications such as computer vision (Ibrahim et al.,2020),natural language processing(Cambria and White,2014),and speech recognition(Haridas et al.,2018).Recently,it has also attracted much attention in the power engineering community(Bose,2017)from both academia and industries.

AI itself has gone through several ups and downs,and interested readers are referred to Buchanan (2005) for more details.The most recent resurgence of AI is powered by deep learning (Le-Cun et al.,2015;Goodfellow et al.,2016),which is part of a broader family of machine learning methods that are based on artificial neural networks with representation learning.On one hand,deep learning can handle a huge amount of data where other machine learning methods often fail.On the other hand,the power industries are obtaining more and more data due to the wide spread of advanced information and communication technologies(Huang et al.,2019)such as phasor measurement units (PMU),micro phasor measurement units (μPMU),and advanced meter infrastructures.As a result,many scholars have been trying to apply deep learning to problems of smart grid dispatch,with the hope of tackling the issues that remain unsolved by traditional methods.This motivated us to write this paper to summarize what has been done already and where deep learning is headed regarding smart grid dispatch.Note that other machine learning methods,such as random forests(Rahman et al.,2020)and logistic regression(Rudin et al.,2012;Eskandarpour and Khodaei,2017),will not be the focus of this paper.

2 Smart grid dispatch problems

Mathematically,smart grid dispatch is an optimization problem that can be formulated as follows:

wherexrepresents decision variables (e.g.,outputs of generators),f(x) represents the objective function (e.g.,total cost of all the generators),andg(x)andh(x) represent equality constraints (e.g.,power balance constraints)and inequality constraints(e.g.,output limits of generators),respectively.Under different assumptions or for different requirements,smart grid dispatch problems will have different formulations.Herein,we summarize some popular formulations that are often used in power engineering.

2.1 Economic dispatch

The economic dispatch problem is the process of allocating generation among different generating units to achieve the minimum operating cost(Wood et al.,2013).It is the simplest formulation of smart grid dispatch and is often used for real-time operation.The formulation is as follows:

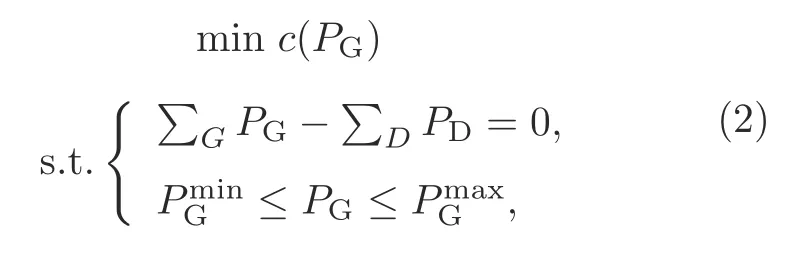
wherePGandPDrepresent the generator outputs and load demands,respectively.Gis the set of power generators andDis the set of load demands.c(PG)is the total cost function,which can be nonlinear(e.g.,quadratic functionc(PG)is often used) or linear (i.e.,c(PG)The first constraint is the power balance constraint,without considering the power flow through transmission lines.The second constraint presents the limits of generator outputs.

The classical economic dispatch problem targets minimization of the operating costs as shown above.With the increasing concern about environmental matters,other costs,such as carbon emission cost,can also be included (Yin et al.,2018).In addition,network loss cost is often considered (Zeng et al.,2014),especially for electricity market applications.

2.2 Optimal power flow

Economic dispatch is quite successful when the flows within transmission lines are at a low level.However,with quickly increasing demand for electricity,transmission lines were soon working close to their capacities,and a fear of line overloading led to the concept of optimal power flow (Carpentier,1979).

As an extension of the classical economic dispatch problem,optimal power flow is an optimization problem that solves the economic dispatch problem and power flow equations simultaneously(Wood et al.,2013).Its original formulation is as follows:

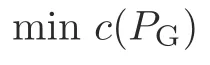
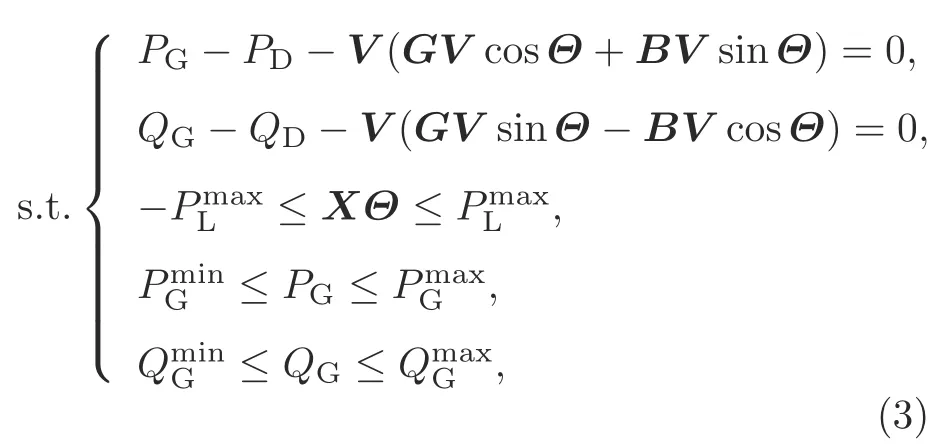
wherePG,QG,PD,QD,V,G,B,andΘindicate the generator active output,generator reactive output,load active demand,load reactive demand,voltage magnitude,the real part of the node admittance matrix,the imaginary part of the node admittance matrix,and the voltage angle difference,respectively.Xis the reactance matrix of transmission lines,andrepresents the transmission capacity.The first two constraints address the power flow equations,the third constraint addresses the transmission line constraints,and the last two constraints address the limits of generator outputs.

The above problem is a highly nonlinear and nonconvex optimization problem,which makes it quite difficult to solve for practical usage.As a result,a linear approximation called direct current (DC)optimal power flow is often used in research and industry.Here,decision variables in the DC optimal power flow formulation correspond to active generator outputs only.Generally,it is believed that DC optimal power flow gives a good approximation of the original optimal power flow problem (i.e.,alternating current(AC)optimal power flow)and is much faster and easier to apply (Wood et al.,2013).DC optimal power flow has the following formulation:

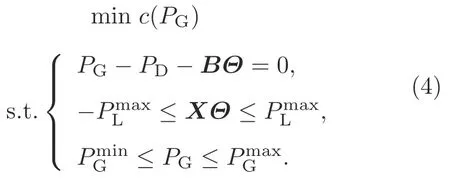
The optimal power flow problem provides a building block for many other smart grid dispatch applications(Chatzos et al.,2020),and is almost the most popular formulation for smart grid dispatch.

2.3 Unit commitment

In economic dispatch and optimal power flow,it is assumed that there areNGgenerating units working in the power system.Under this assumption for the economic dispatch problem and the optimal power flow problem,we aim to find an optimal operating point for grids.Nevertheless,the optimal subset of the complete set of generating units remains undecided,which results in the problem of unit commitment (Sheble and Fahd,1994;Padhy,2004;Tejada-Arango et al.,2020).

A general formulation of unit commitment is as follows:

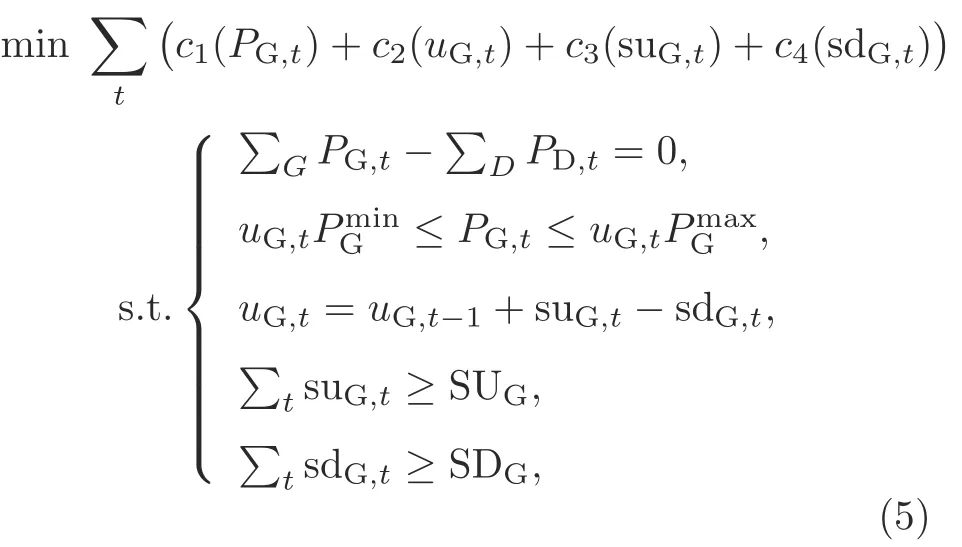
wherec1(·),c2(·),c3(·),andc4(·) indicate the fixed cost,variable cost,startup cost,and shutdown cost of generating units,respectively.uG,t,suG,t,and sdG,tindicate the commitment decision,startup decision,and shutdown decision,respectively.The first constraint addresses the power balance constraints,the second constraint addresses the generator output constraints,the third constraint addresses the unit status,and the last two constraints address the minimum up-and down-time constraints.

Unit commitment is often used for day-ahead generation scheduling.The desired output is the commitment status,which is binary.As a result,the unit commitment problem is a mixed-integer optimization problem,which is more complicated than the economic dispatch problem.

2.4 Security-constrained dispatch

Contingencies are things that might happen to a system for various reasons,for example,natural disasters(Huang et al.,2017a,2017b)or human attacks(Xiang et al.,2018).The above formulations,however,do not consider contingencies,which can lead to load shedding or even large blackouts when disruptions happen.As a result,it is necessary to take into account contingencies as constraints in smart grid dispatch problems.

Contingency analysis models single-failure events (e.g.,one line fails) or multiple equipment failure events (e.g.,two transmission lines fail at the same time) (Wood et al.,2013).According to whether corrective actions are allowed when integrating contingencies in smart grid dispatch formulations,security-constrained dispatch problems can be categorized into preventive security-constrained dispatch and corrective security-constrained dispatch(Xu et al.,2014).Taking the contingencies of transmission line outages in DC optimal power flow problems as an example,the preventive securityconstrained optimal power flow problem can be formulated as follows:

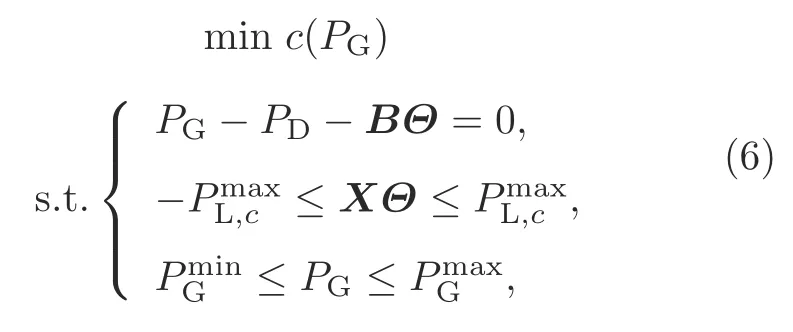
where the subscriptcindicates the set of contingencies that will be taken into account.

Similarly,we can present the formulation of corrective security-constrained optimal power flow problems as follows:

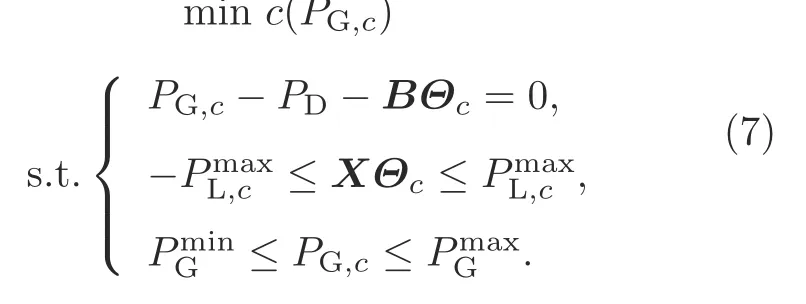
Note that contingencies will greatly increase the scale of the optimization problem,and therefore the solution of smart grid dispatch problems will be much harder.

3 Deep learning solutions

Many methods have been developed for smart grid dispatch problems.For example,Newton-based methods (Sun et al.,1984) and interior-point methods (Capitanescu and Wehenkel,2013) have been thoroughly investigated and widely used.However,these methods have to repeatedly solve the challenging dispatch problems,which could hardly meet the fast-growing requirements of reliability and computational efficiency.As a result,in contrast to the above mathematical optimization methods,scholars began to investigate the application of deep learning methods for smart grids.After briefly introducing the deep learning basics in Section 3.1,we review the recent progress.This progress can be divided into three categories,whose logic,along with the logic of traditional mathematical optimization methods,is summarized in Fig.1.Herein,type-1,type-2,and type-3 correspond to end-to-end learning,constraint set learning,and iterative process learning,respectively,and they will be reviewed in Sections 3.2-3.4.Different methods provide different pipelines to derive dispatch decisions from a given system state.Our taxonomy of deep learning solutions is shown in Table 2.

3.1 Deep learning basics

We focus on deep learning,especially deep neural networks in this study.Let us useto represent the input data of smart grid dispatch problems(e.g.,power system state),andto represent the output data (e.g.,grid dispatch decision).The aim of deep learning methods is to derive an optimal modelf(·)to capture the relationship betweenandIn other words,the following problem will be minimized to learn the pattern betweenand

Here,andrepresent the input and output parts of a given samplei.Functionℓ(·) measures the difference betweenf() andand is also known as the loss function or empirical risk.For classification problems,we often use 0/1-loss,namely,1 ifFor regression problems,square-loss is often used,namely,

3.2 End-to-end learning

As illustrated in Fig.1,smart grid dispatch end-to-end learning refers to training a complex machine learning model to directly learn the inputs and outputs of the original optimization problems.The power of the end-to-end learning philosophy has been demonstrated in many tasks,for example,image recognition (He et al.,2016),self-driving cars(Bojarski et al.,2016),and three-dimensional (3D)object detection (Zhou Y and Tuzel,2018).Thus,the straightforward brute-force technique has been almost the most popular direction in deep learning applications.Typical works on end-to-end learning methods for smart grid dispatch problems are listed in Table 2.

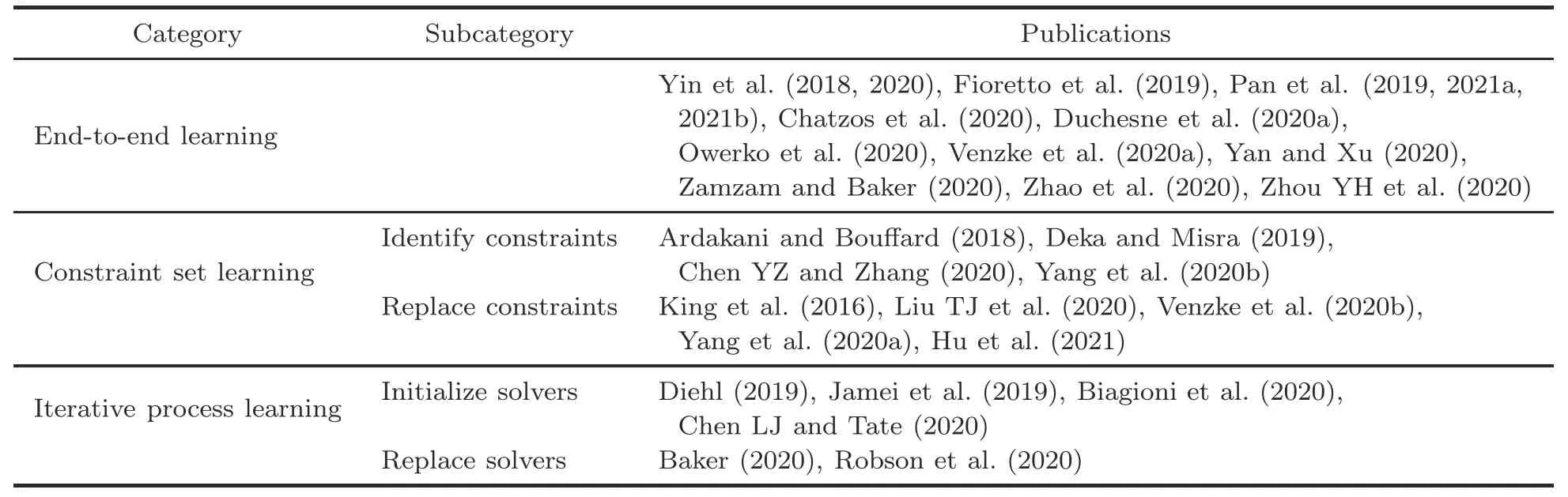
Table 2 Taxonomy and representative publications on deep learning solutions

Fig.1 Logic summary of deep learning solutions

Pan et al.(2019) developed a deep neural network approach called DeepOPF for the DC optimal power flow problem.The DeepOPF approach uses a multi-layer feed-forward neural network to learn the mapping between power demand and generator output.In this paper,generator limit constraints were guaranteed by the Sigmoid activation function,and a penalty function was proposed to deal with transmission line limit constraints.Because the line limits cannot be exactly satisfied,a post-processing procedure was activated when lines got overloaded.Note that power balance equations were there to derive line flow when power demands and power generators were derived.

Based on the above work,Pan et al.(2021a)extended the DeepOPF approach to the securityconstrained DC optimal power flow problem.Their case studies showed that the proposed approach can speed up the computation by up to two orders of time,compared to the Gurobi solver (Gurobi Optimization,2019).As a cost,18.3%of solutions might be infeasible before the post-processing procedure in the worst case,and 0.2% optimality loss on average would be unavoidable.

Pan et al.(2021b) also investigated the Deep-OPF approach for the AC optimal power flow problem.Because explicit expressions of penalty gradients are unavailable,AC power flow equations make the widely used training methods (e.g.,stochastic gradient descent(Le et al.,2011)and Adam(Kingma and Ba,2015)) fail.Thus,a two-point zero-order optimization method was proposed in Pan et al.(2021b) to compute the estimated gradient during training.The effectiveness of the proposed method was verified through a small-scale test system,but evaluation of DeepOPF for medium-or large-scale AC optimal power flow problems still needs further research.

As an improvement of DeepOPF,DeepOPF+was recently proposed (Zhao et al.,2020).It is also based on a multi-layer feed-forward neural network,but tries to deal with the feasibility issue that remains in previous methods.The idea is to calibrate the generation limits and transmission line limits during training dataset preparation.The benefit is that a post-processing procedure is no longer required to guarantee the generation limits and transmission line limits.As a result,further computation acceleration can be guaranteed.It was also reported that a larger calibration magnitude will lead to a larger optimality loss,while a higher feasibility rate can be achieved.

Encouraged by Pan et al.(2019),Zamzam and Baker(2020)investigated how to learn the mapping from system loading to optimal generation setpoints and voltages with deep neural networks for the AC optimal power flow problem.Similar to the limitation in Pan et al.(2019),operational constraints cannot be guaranteed directly by the deep learning method in Zamzam and Baker (2020).To alleviate this issue,a fast iterative procedure based on the power flow problem is required to recover a feasible solution.Note that transmission line constraints were ignored in Zamzam and Baker(2020).

To analyze the robustness of deep neural network methods used in the above works,Venzke et al.(2020a) introduced a framework based on mixed-integer linear programming to obtain worstcase guarantees for DC optimal power flow problems.Three conditions were considered:(1) maximum constraint violations,(2) maximum distances between the predicted and optimal decision variables,and (3) maximum distance between the predicted and optimal solution values.The results on a range of PGLib-OPF networks (Babaeinejadsarookolaee et al.,2021) up to 300 buses showed that the worst-case guarantees can be up to one order of magnitude larger than the empirical lower bounds by conventional methods.Nevertheless,the worst-case guarantees can be reduced to an acceptable level by training on a larger input domain.

Fioretto et al.(2019) explored a deep learning approach called OPF-DNN for highly efficient and accurate solutions of AC optimal power flow problems.The OPF-DNN method consists of a deep neural network architecture and Lagrangian duality.Here,Lagrangian duality was used to deal with the physical and engineering constraints.The OPF-DNN method was verified on systems up to 300 buses and results showed that it is faster than the DC optimal power flow approximation solved with IPOPT (Wächter and Biegler,2006)by at least two orders of magnitude.

The OPF-DNN method was revisited in Chatzos et al.(2020).The authors improved the algorithm design and training procedures,and through the case study in a French 3400-bus transmission system,the effectiveness of the proposed framework on largescale power systems was verified.The biggest finding was that high-fidelity approximations of large-scale optimal power flow problems can be solved within milliseconds.

Because smart grids can be viewed as a graph,Owerko et al.(2020) proposed using graph neural networks in an imitation learning framework to solve AC optimal power flow problems.Graph neural networks(Wu ZH et al.,2021)belong to a class of neural networks that map the inputs to the output with consideration of the underlying graph.Case studies on the IEEE 30-bus system and IEEE 118-bus system were provided.The results showed that graph neural networks can lead to lower root mean squared errors.

Zhou YH et al.(2020) applied deep reinforcement learning to solve the AC optimal power flow problem.A deep neural network agent was trained by the state-of-the-art proximal policy optimization algorithm to derive an optimal policy for the reinforcement learning framework.To further increase the training speed and performance of the deep neural network agent,they used another independent neural network to learn a better initialized policy.

Yan and Xu (2020)applied a Lagrangian-based deep reinforcement learning method to solve realtime optimal power flow problems.The Lagrangian relaxation approach was proposed to deal with the operational constraints,and a policy model based on a deep deterministic policy gradient was used to update parameters of the deep neural network.Simulations were conducted to show that the proposed method can derive decisions continuously in real time for the IEEE 118-bus system.

Duchesne et al.(2020a) dealt with the dayahead unit commitment and economic dispatch decision ranking problem with deep neural networks.This problem is different from the above problems because it belongs to the field of reliability management for smart grid dispatch.Running a very large number of security-constrained optimal power flow problems for all the day-ahead decisions is impractical,so a deep learning method was used to assess day-ahead decisions and rank them according to next-day operating costs.Multi-task learning was also used to provide more information about different cost values such as preventive redispatch cost,preventive load shedding cost,and preventive wind curtailment cost.

Yin et al.(2018)used a deep learning method to replace the traditional automatic generation control method.The method consists of two deep neural networks connected by a“selector,”which was designed to determine the optimal next state in the next states predicted by the first neural network.A“relaxed operator”was used after the second neural network to ensure that the constraints of generating units are met.The feasibility of the proposed method was verified through the IEEE New-England power system,Hainan power grid,and IEEE 118-bus power system.

Yin et al.(2020)extended the work in Yin et al.(2018) to scenarios where the number of generators and the topology of systems are not fixed.An expandable deep learning method was proposed for dynamic expandable future smart grids.The proposed method consists of basic deep neural networks and expanding operation which makes the neural networks expandable.A 118-bus power system and a 13 659-bus system were used to verify the effectiveness of the proposed method.

3.3 Constraint set learning

While end-to-end learning is elegant and powerful,it may be inefficient (Glasmachers,2017) and the operational constraints in smart grid dispatch problems can hardly be satisfied exactly.An alternative is to use deep learning to predict the constraint set for mathematical optimization models (Type-2 in Fig.1).The constraint set learning method works as an intermediate step between deep learning and mathematical optimization.As a result,traditional algorithms such as interior-point methods and simplex methods can be significantly accelerated.In fact,some complex smart grid dispatch problems might even be downgraded to have analytic solutions when the filtered constraints are simple.

A hot field is active constraint set learning(Misra et al.,2019),where active constraints mean the constraints that are satisfied with equality in the corresponding optimization problem.For example,Deka and Misra (2019)took advantage of deep neural network based classifiers to learn optimal active constraints from uncertainty realization.Given an uncertain injection scenario,the proposed classification method can derive the corresponding active constraints,which can then be used to calculate the results of DC optimal power flow problems.It was shown that the deep learning method is superior to the traditional ensemble policy method in both speed and performance.

Chen YZ and Zhang (2020) proposed a deep neural network to learn the mapping between power loads and the optimal system cost,but interpreted the gradient of neural networks as dual variables,which could be used to identify active constraints in the DC optimal power flow problem.The proposed method is error-correcting and proved to be an order of magnitude faster than the state-of-the-art linear programming solvers.

Yang et al.(2020b) proposed a deep learning based pre-screening method to identify active constraints of security-constrained economic dispatch problems.To deal with topology changes that might occur in a system,a fast tuning strategy based on transfer learning was also provided.The authors verified the effectiveness of their method on the IEEE 30-bus system,IEEE 118-bus system,and a practical 661-bus utility system.

Umbrella constraints are different from active constraints.They are the constraints that form the feasible set of solutions,which makes active constraints a subset of umbrella constraints in the same problems (Ardakani and Bouffard,2018).Regarding the umbrella constraint set,deep learning is not yet applied for smart grids.A related work is Ardakani and Bouffard (2018),in which a single-layer neural network was applied to learn the optimal umbrella constraints for the security-constrained optimal power flow problem.The input is a specific demand scenario and the output is the umbrella set corresponding to that scenario.A customized training algorithm was proposed to replace the traditional backpropagation algorithm to avoid false negative errors.However,the proposed method has weaker learning ability than deep learning methods,and thus 2864 neural network models are required for 2864 constraints.

Both active constraint set learning and umbrella constraint set learning aim to identify effective constraints for mathematical optimization.In addition,deep learning methods can be used to replace some constraints for smart grid dispatch problems.For example,Yang et al.(2020a) and Hu et al.(2021)focused on replacing power flow equations with deep learning methods.Here,Yang et al.(2020a) constructed a deep neural network to learn the probabilistic power flow calculation for smart grid dispatch,and Hu et al.(2021)encoded physical knowledge of the grid to regularize neural networks to solve the overfitting problem.

Venzke et al.(2020b)focused on the more challenging AC optimal power flow problems with dynamic security constraints.The authors first used a deep neural network to solve the AC optimal power flow problem including dynamic security constraints.Then,they reformulated the nonlinear activation function with binary constraints and the deep neural network was transformed into mixed-integer constraints.Taking into account the above constraints in a mathematical optimization model,the authors tackled the issue of how to consider dynamic security constraints for optimal power flow problems.

Liu TJ et al.(2020) also investigated how to take advantage of deep learning methods to incorporate dynamic security constraints into optimal power flow problems.First,a Bayesian neural network was trained by the“Bayes by Backprop”method (Blundell et al.,2015) for confidential dynamic security assessment.Then,a security-constrained optimal power flow problem was reformulated by replacing dynamic security constraints with the above neural network model.Finally,the Bayesian optimization method was used to solve the smart grid dispatch model embedded with deep learning constraints.

King et al.(2016)focused on transient stabilityconstrained optimal power flow problems.The authors proposed to replace the dynamic and transient stability constraints with a critical clearing time constraint.Then,the critical clearing time constraint was approximated by a neural network model.As a result,dynamic simulations during traditional optimization methods were no longer required in the proposed method,and the computational burden of dynamic simulations was therefore removed.

The performances of constraint set learning and end-to-end learning were compared in a simple way in Guha et al.(2019).The results on the IEEE 30-bus system and IEEE 118-bus system showed that the constraint learning method can be more effective.However,we need to note that a more thorough comparison is required to lead to a general conclusion.

3.4 Iterative process learning

Smart grid dispatch problems are traditionally formulated as mathematical optimization problems and then solved by an iterative process such as Newton-based methods(Sun et al.,1984)or interiorpoint methods (Capitanescu and Wehenkel,2013).However,the iterative numerical methods might result in a failure of convergence due to a bad initialization point (Baker,2019).Moreover,Newton-based methods have to calculate a full Jacobian matrix(e.g.,Newton-Raphson method) or an approximate Jacobian matrix(e.g.,quasi-Newton method)during iterations,which is time-consuming and might even be numerically unstable(Baker,2020).To deal with the above issues,deep learning following the formulation of the mathematical optimization problem is also investigated.

Because a good initialization point can avoid poor local optimum and speed up the convergence process,Jamei et al.(2019) proposed a metaoptimizer to initialize interior-point solvers.Inspired by meta learning,the meta-optimizer is based on a neural network model that could be trained to learn the pattern between the dispatch problem formulation and initialization point.The loss function was defined as the number of iterations to reach an optimal solution.Experiments verified that the convergence process could be accelerated.

Based on the results from DC power flow calculation,Chen LJ and Tate (2020) proposed a onedimensional convolutional neural network method to obtain initial values of voltage magnitude and phase values for Newton-Raphson-based AC power flow problems.Experiments on the IEEE 118-bus system and PEGASE 2869-bus system showed that the proposed method could achieve more than 30% reduction in computation time and 49.54%-66.47%reduction in solution iterations.

Diehl(2019)proposed using a graph neural network method to warm-start the AC optimal power flow solvers.Results on the Illinois 200-bus system showed that the proposed method would achieve 25%reduction in computation time compared to the IPOPT solver.In fact,the proposed method would even be slightly faster than the IPOPT method warm-started by the DC optimal power flow.

Biagioni et al.(2020)focused on the distributed formulation(i.e.,the alternating direction method of multipliers)of DC optimal power flow problems.The authors proposed a recurrent neural network based on the gated recurrent unit to predict the equilibrium values and accelerate the iterations.Case studies on the IEEE 14-bus system,IEEE 118-bus system,and RTE 2848-bus system verified the effectiveness of the proposed method.

Baker (2020) used a deep neural network with feedback to learn the Newton step as follows:

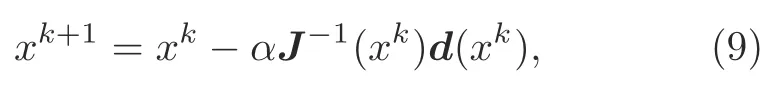
wherexkis the solution at iterationk,J-1(xk) is the Jacobian matrix at iterationk,d(xk) is a vector of the Karush-Kuhn-Tucker (KKT) conditions at iterationk,andαis an optional step-size parameter.Case studies showed that the deep learning method can avoid singular Jacobian matrices and ill-conditioned matrices in Newton-based methods,and the computational efficiency improvement will be large for large power grids.

Robson et al.(2020) proposed a deep-learningbased method to iteratively solve optimal power flow problems.First,a neural network model was used to generate a reduced optimal power flow model by removing the predicted non-binding constraints.Then,the reduced model was extended by iteratively checking and adding violated constraints during iterations.The parameters of the neural network model were determined by minimizing the meta-loss function which is defined by the computational cost of the warm-stated optimal power flow problems.Because this loss function is not differentiable,particle swarm optimization rather than back-propagation was used to train the model.

4 Challenges

The fast development of smart grid and AI will bring about great opportunities.Much progress has been made in smart grid dispatch via deep learning methods;however,many issues in this field still require further research and some problems even remain untouched.Herein,we discuss several significant challenges based on our observations.

4.1 Data availability,security,and privacy

Deep learning is a data-driven method;so,datasets that could be used to train deep learning models and evaluate their performance are of vital importance (Venzke et al.,2021).In fact,to realize its greater learning ability,deep learning requires more data than traditional machine learning methods.However,while various public datasets are available for fields such as computer vision (Prabhu and Birhane,2020)and natural language processing(Dror et al.,2017),very few electric power system datasets are publicly available at the present time(Ruan et al.,2021).Although we can easily find the data for many power networks (e.g.,in Coffrin et al.(2019)),current research often has to run simulation tools (e.g.,MATPOWER (Zimmerman RD et al.,2011)) to generate training samples for deep learning.This raises an obstacle for deep learning experts who are not familiar with how power grids work.The availability of power system datasets,especially real-world power system datasets,is still urgent.

Data security and privacy are other issues that often accompany deep learning methods (Wu C et al.,2019).A promising direction is distributed deep learning,especially federated learning (McMahan and Ramage,2017;Kairouz et al.,2019;Li et al.,2020;Huang et al.,2021),which could enable collaborative machine learning while the raw data remain distributed.Another direction is to develop small sample learning techniques (Zhang et al.,2018),for example,few-shot learning (Ravi and Larochelle,2016) and zero-shot learning (Changpinyo et al.,2016).In case we cannot gather enough data to construct a training dataset that we need,data augmentation (Shorten and Khoshgoftaar,2019) can also help.

4.2 Model robustness and explainability

Deep learning methods have already shown their power in mastering games(Silver et al.,2017),quantifying behaviors(Mathis et al.,2018),and so forth.However,how significantly deep learning will impact real-world power systems still requires investigation.There is no doubt that deep learning methods,although vulnerable(Papernot et al.,2016)sometimes,can be widely used in fields that are not so securitysensitive.However,power systems are critical infrastructure and are very sensitive,so robust deep learning methods are necessary.This issue is particularly challenging because the vulnerability of deep learning methods for power systems has been shown(Chen YZ et al.,2018;Venzke and Chatzivasileiadis,2021).

Although traditional numerical methods for smart grid dispatch problems can sometimes fail to converge,deep learning methods will always generate a solution.This is not at all an advantage,however,because deep learning methods are widely viewed as black-box models,which means that we cannot explain the solution they provide.This will hinder the application of deep learning methods,especially in fields like smart grids.In general,there are two directions to alleviate the explainability issue:(1)interpreting the deep learning models with visualization(Chatzimparmpas et al.,2020)and(2)building interpretable deep learning models(Duchesne et al.,2020b).

5 Conclusions

Artificial intelligence has attracted extensive attention recently,and it is beginning to revolutionize power grids,a typical representation of critical infrastructure systems.As a core problem for power system operation,smart grid dispatch has been reviewed in this paper from the perspective of deep learning,which is,so far,the most advanced AI technique.We have provided our taxonomy of all the deep learning solutions which can be divided into three categories(end-to-end learning,constraint set learning,and iterative process learning).Representative works of each type have been carefully reviewed,and the main challenges regarding deep learning methods for smart grid dispatch have also been discussed.It can be concluded that much more effort is required to promote deep learning methods for smart grid dispatch,and we expect that this paper will provide a helpful review for researchers who are entering this interdisciplinary area of smart grids and AI.

Contributors

Gang HUANG drafted the paper.Gang HUANG,Fei WU,and Chuangxin GUO revised and finalized the paper.

Compliance with ethics guidelines

Gang HUANG,Fei WU,and Chuangxin GUO declare that they have no conflict of interest.