考虑政府参与的环境NGO与WEEE处理商演化博弈研究
孙珂珂,张海珍,李 鑫
(1. 青岛大学商学院,青岛 266061;2. 菏泽学院商学院,菏泽 274000)
目前,中国已经进入家电报废高峰期,报废数量年均增长20%,预计2021年报废家电将达到1.37亿台。废旧家电的非法拆解和处理会产生大量污染物如溴代阻燃剂、重金属等,对大气、土壤和水环境造成严重污染。废旧家用电器无害化回收处理已经成为全球共识,回收处理过程中出现的相关问题亦引起政府、环保组织以及国内外众多学者的重点关注。中国的废旧家电回收处理业务是WEEE处理商在政府相关政策的指导下执行运作,即政府出台相应的法规政策规范家电行业发展,营造有利于回收处理行业可持续发展的环境与条件,WEEE处理商遵循市场规律运营。WEEE处理商是否开展某项回收处理业务,取决于政府激励下某项回收处理业务获得的净盈利[1-8]。为落实生产者责任延伸制度、推进废旧家电回收处理工作再上新台阶,国家发改委于2020年5月出台《关于完善废旧家电回收处理体系推动家电更新消费的实施方案》,提出要完善行业标准规范、政策体系,建立有序、高效的废旧家电回收体系。目前,已有众多研究构建了多种废旧家电回收体系,如废旧家电逆向物流回收体系[9-12]、废旧家电网络信息平台[13]等。此外,现实中影响WEEE回收的相关因素包括回收渠道[14]、回收价格[15]和回收成本[16-17]等。目前,考虑政府参与情形下环境NGO(即环境非政府组织)与WEEE处理商之间联系的研究成果较少。环境NGO作为独立组织,不以商业和营利为目标,能够宣传和普及环保意识,推动和促进企业与消费者参与环境保护活动,激励WEEE处理商策略转型等。综上,本文基于考虑政府参与废旧家电回收过程中环境NGO与WEEE处理商互相合作与博弈行为,探讨双方在不同情形下的均衡策略及条件,促使双方选择最优决策以保障环保工作的顺利开展。
1 演化博弈模型
1.1 假设与符号定义
模型包含环境NGO和WEEE处理商两个博弈主体,WEEE处理商考虑自身的成本和利润等因素会做出不同的决策,即普通处理和无害化处理;由于环境NGO非商业、非营利的特点,盈利来源一般为消费者的捐款,其自身利益会受到消费者的约束和影响,也会做出两种不同的决策即监管和不监管。基于此,本文提出以下假设:
假设1:博弈双方均为有限理性,环境NGO的策略集为{监管,不监管};WEEE处理商的策略集为{无害化处理,普通处理}。环境NGO选择监管策略的概率为x(0≤x≤1),选择不监管策略的概率为1-x,WEEE处理商选择无害化处理和普通处理策略的概率分别为y(0≤y≤1)和1-y。
假设2:与环境NGO有关的假设。环境NGO潜在收益为E1,监管需付出成本为C1。
假设3:与WEEE处理商有关的假设。WEEE处理商选择普通处理时获得的收益为E2,无害化处理需投入一定的成本为C2(如购买无害化处理设备和相关技术研发等),收益增加概率为α2(0≤α2≤1)。
假设4:环境NGO和WEEE处理商的混合假设。双方共同选择积极策略时,环境质量状况得到改善,环境NGO获得额外的社会效益,收益增加概率为β0(0≤β0≤1)。WEEE处理商获得环境NGO的扶持帮助,收益增加概率为α1(0≤α1≤1)。WEEE处理商保持现状时,环境NGO监管时发现处理商违规行为,敦促政府对其处罚,使WEEE处理商的收益减少,减少概率为β(0≤β≤1);由于环境NGO监管得当,政府将处罚WEEE处理商的罚金赠予环境NGO作为奖励。双方共同选择消极策略时,环境污染加剧,政府接到消费者举报两者消极行为的概率为θ(0≤θ≤1),若接到消费者举报,政府对两者分别处以罚金为f1、f2的处罚。
1.2 模型构建
基于以上假设,构建环境NGO与WEEE处理商不同策略下的演化博弈收益矩阵见表1。

表1 环境NGO与WEEE处理商的博弈支付矩阵

EX1=y[(1+β0)E1-C1]+(1-y)(E1+βE2-C1)
(1)
EX2=yE1+(1-y)(E1-θf1)
(2)
(3)
根据Malthusian动态方程[18],构建环境NGO选择监管情况下的复制动态方程为
(4)

EY1=x[(1+α1)E2-C2]+(1-x)[(1+α2)E2-C2]
(5)
EY2=x(1-β)E2+(1-x)(E2-θf2)
(6)
(7)
由此得WEEE处理商选择无害化处理情况下的复制动态方程为
(8)
2 演化博弈稳定性分析
根据Friedman[19]提出的分析方法检验均衡点的性质,即由该系统相应的雅克比矩阵J的行列式detJ和迹trJ来判定。当且仅当detJ>0,trJ<0时,该均衡点具有稳定性。联立式(4)、式(8)复制动态方程,得该系统的复制动态方程组为

(9)
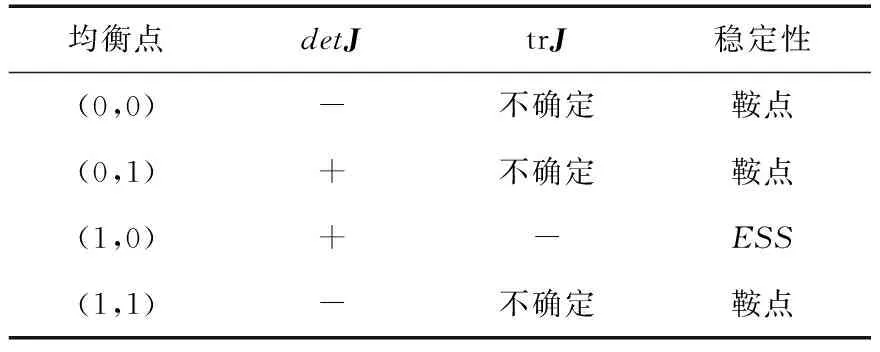
令F(x)=0,F(y)=0,可得(0,0)、(0,1)、(1,0)、(1,1)、(x0,y0)5个均衡点,对其所描述的动态系统,均衡点对应的detJ和trJ见表2。在(x0,y0)处,trJ=0不满足trJ<0这一条件,因此(x0,y0)不是演化稳定均衡点,不再计算U值。

表2 系统各局部均衡点detJ和trJ的取值
2.1 环境NGO群体策略稳定性分析
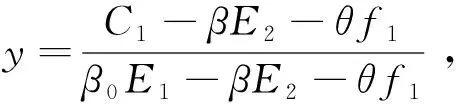

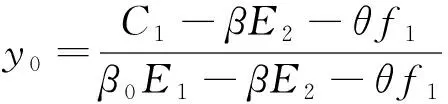
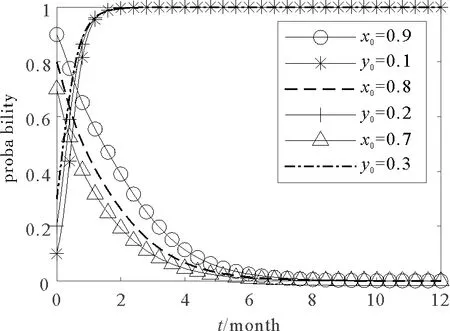
②若C1-βE2-θf1>β0E1-βE2-θf1,即C1>β0E1,恒有y ③若0 ②若α2E2+θf2-C2>α2E2+θf2-α1E2-βE2,即α1E2+βE2>C2,则恒有x ③若0<α2E2+θf2-C2<α2E2+θf2-α1E2-βE2,即0 当βE2+θf1 表3 系统均衡点的稳定性分析 图1 稳定点(0,0)的仿真结果 当βE2+θf1 表4 系统均衡点的稳定性分析 图2 稳定点(1,0)的仿真结果 当β0E1 表5 系统均衡点的稳定性分析 图3 稳定点(0,1)的仿真结果 当β0E1>C1且α1E2+βE2>C2时,4个均衡点的稳定性见表6。此时,只有(1,1)点符合detJ>0,trJ<0的条件,因此该点为系统的稳定均衡点,系统的演化稳定策略为监管、无害化处理。此时设参数值E1=10,E2=6,C1=3,C2=4,α1=0.8,α2=0.3,β=0.1,β0=0.4,f1=4,f2=3,θ=0.5,环境NGO与WEEE处理商选择策略的初始值分别为(0.4,0.6),(0.3,0.5),(0.2,0.4),由Matlab得到的系统仿真见图4。由稳定条件β0E1>C1、α1E2+βE2>C2可知,当环境NGO增加的收益高于监管成本时,环境NGO倾向于监管策略;当WEEE处理商转型成本低于环境NGO给予的扶持福利和采取普通处理损失的收益总和时,WEEE处理商更倾向于无害化处理策略。结合实际情况,环境NGO的盈利来源为消费者捐款和政府拨款、WEEE处理商的转型依赖于扶持福利和政府措施,此时,政府需引导和强化消费者、WEEE处理商的无害化处理意识,实施相关奖惩措施,推进废旧家电的无害化处理。 表6 系统均衡点的稳定性分析 图4 稳定点(1,1)的仿真结果 当β0E1>C1且α1E2+βE2>C2时,环境NGO与WEEE处理商选择策略的初始值分别为(0.4,0.6),此时设参数值E1=10,E2=6,C1=3,C2=4,α2=0.3,β=0.1,β0=0.4,θ=0.5,分别讨论f1、f2、α1对仿真结果的影响,如图5、图6所示。可知,环境NGO和政府给予的扶持程度是影响WEEE处理商向无害化处理转型速度快慢的关键因素。政府惩罚力度越大、环境NGO扶持力度越大,企业转型速度就越快。应加大对成功无害化转型WEEE处理商的宣传力度,出台相应的政策扶持、提高相关的补贴,加快WEEE处理商的转型速度。 图5 f1、f2对仿真结果的影响 图6 α1对仿真结果的影响 本文基于演化博弈法研究讨论了废旧家电回收中环境NGO与WEEE处理商之间博弈关系,分析总结4个稳定策略。研究结果显示,WEEE处理商的转型速度与政府和消费者的参与度、环境NGO给予的宣传福利、转型成本等因素呈现线性关系。若政府和消费者不参与废旧家电无害化回收处理,单靠环境NGO和WEEE处理商,废旧家电无害化回收处理难以达到理想状态即绿色环保、无污染的回收处理过程。因此,政府应提高无害化处理政策的支持程度,增加污染惩罚力度,提高消费者参与的积极性,推进废旧家电的无害化处理。本研究只考虑了废旧家电参与群体中环境NGO和WEEE处理商的行为策略,今后将引入奖惩机制,研究制造商、政府等多主体策略行为的演化问题。

2.2 WEEE处理商群体策略稳定性分析
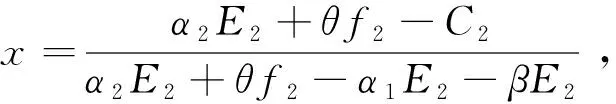

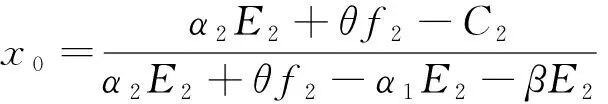


3 结果与讨论








4 结论

