基于局部相似性的非平滑非负矩阵分解

张逸群，彭 冲

(青岛大学计算机科学技术学院，青岛 266071)

随着网络信息时代的到来，人们在使用互联网时产生了海量的数据，这些数据可以使用高维矩阵形式存储于计算机中。处理高维数据矩阵时，矩阵分解算法可以找到两个或多个低维矩阵来近似原始数据，用低维数据来表示高维数据，这项技术广泛应用于图像识别、信号识别和视频处理等领域[1]。针对条目为非负元素的数据如图像和文档，非负矩阵分解(Nonnegative Matrix Factorization，NMF)算法寻求两个非负的因子矩阵，使二者乘积可以逼近原始矩阵[2]。在面部识别问题中，学习的基础图像是局部的而不是整体的，类似于面部某个抽象的部分，将基矩阵和系数矩阵进行线性组合即可由部分组成整体[2]。因此NMF算法在表示原有数据信息时所需数据元素更少，存储数据所需空间资源就更少，便于简化计算。该算法的非负约束能使分解所得矩阵具有随机稀疏性即局部特征更加明显，若要保证更稳定的稀疏性，还需要添加相应的约束条件[3]。Liu等[4]基于Hoyer[5]提出的非负稀疏编码方法，引入KL散度，提出稀疏非负矩阵分解(Sparse Nonnegative Matrix Factorization)。Hoyer[6]在此基础上又引入一种非线性稀疏函数来约束分解后矩阵的稀疏性。上述算法单独对基向量与编码向量稀疏性进行约束，而由于矩阵分解后两个矩阵“相乘”的性质，施加稀疏约束一般只能使其中一个矩阵具有稀疏性。基于此问题，非平滑非负矩阵分解算法(Non-smooth Nonnegative Matrix Factorization，nsNMF)在目标函数中引入了一个“平滑”矩阵，使基矩阵和编码矩阵都具有稀疏性[7]。该算法假设数据都是线性分布的，如果数据分布在非线性结构例如流形结构时，聚类效果会受到影响。实际应用中，高维数据通常驻留在低维子空间中，恢复这些子空间需要一个自我表达性假设。现有研究表明，数据内的局部结构非常重要[8]。本文提出一种新的非平滑非负矩阵分解算法，将局部相似性学习作为约束项整合到算法模型中，同时加入核函数，以期解决数据线性不可分时聚类效果差的问题。

1 相关工作介绍

经典NMF算法无法控制分解后矩阵的稀疏程度，无法有效挖掘数据间的几何结构。nsNMF可以保证稀疏性，但没有考虑数据间的几何结构。本文提出基于局部相似性的非光滑非负矩阵分解算法，通过局部相似性约束项和核函数，深度挖掘原始数据间的几何结构，提高聚类精度。

1.1 局部相似性

高维数据通常会驻留在低维子空间中，恢复这些子空间通常需要一个自我表达性的假设，即数据可以用表示矩阵Z和原矩阵X的乘积来近似表示原数据X，表示为

X≈XZ

(1)

将数据限制为列的凸组合，如果两个数据点xi和xj彼此接近，那么它们的相似性Zij应该很大；否则，Zij应该很小[9-10]。因此引出如下优化问题。

(2)

用矩阵形式可以表示为

(3)

其中，1n代表长度为n，元素全为1的向量；diag()代表取括号内矩阵的对角矩阵；Tr()代表括号内矩阵的迹。由于本文的基本问题是将X分解为X*W*VT，因此用W*VT来代替Z，再引入上文所述的平滑矩阵S，因此得到Z=WSVT。

1.2 nsNMF

非平滑非负矩阵分解引入了一个平滑矩阵，将数据矩阵X进行如下分解

X=USVT

(4)

引入的平滑矩阵用S表示

(5)

其中，I是单位矩阵，参数θ取值范围满足0≤θ≤1，q为矩阵的列数。当θ=0时，式(5)为普通NMF算法；当θ=1时，S与其他任意的矩阵相乘，得到的矩阵具有如下性质：矩阵中的元素是与S相乘的矩阵的均值。由于S的平滑性，即可使得基矩阵U和编码矩阵V具有一定的稀疏性。

2 本文算法

2.1 目标函数

首先，算法的目标函数为

(6)

将目标函数展开，得

O=Tr[φ(X)Tφ(X)]-2Tr[φ(X)Tφ(X)WSVT]+Tr[φ(X)Tφ(X)WSVTVSTWT]+λTr(WTDVST)

(7)

2.2 目标函数的迭代求解

设计乘性迭代算法来迭代求解W和V，目标的拉格朗日方程表示为

L=O+Tr(ΩWT)+Tr(ΨVT)

(8)

其中，Ψ=[ψij]，Ω=[φij]是两个矩阵，ψij和φij分别是约束uij≥0,vij≥0的拉格朗日乘子。将W和V取偏导，令φ(X)Tφ(X)=K[11]，得

(9)

(10)

由Karush Kuhn Tucker(KKT)条件及Ωijwij=0，ψijvij=0，得

(-2KVST+2KWSVTVST+λDVST)wij=0

(11)

(-2KWS+2VSTWTKWS+λDWS)vij=0

(12)

整理式(12)得到如下迭代规则

(13)

(14)

此迭代规则概括为算法1：

输入：原始数据X，初始化W和V，模型的参数λ，平滑矩阵参数θ。

(1) 设置最大的迭代次数和阈值,开始迭代计算；

(2) 设置t=1，计算目标函数值，判断是否收敛；

(3) 根据式(17)计算W；

(4) 根据式(18)计算V；

(5)t=t+1,跳转至第二步直到收敛；

返回W，V。

3 实验结果与分析

对比实验在MatlabR2018a，Intel(R)Core(TM)i5-8500T CPU环境下完成。对比算法选取经典的NMF[2]算法及其变体RMNMF[12]、CNMF[10]和ONMF[13]。

3.1 实验数据集

选取3个开源数据集，包括1个手写数字数据集Semeion[14](收集约80人书写的1 593个手写数字，扫描拉伸尺寸为16×16)，两个人脸图像数据集Jaffe[15](收集10名日本女性拍摄的含有7种面部表情图片，共213张，每张像素为26×26)和PIX10[16](包含10名拍摄者100张灰度图像，每名拍摄者包含10张100×100像素的图片)。上述数据集的图像经处理后以灰度值形式存于二维矩阵中，受篇幅所限，仅展示部分数据集，如图1所示。

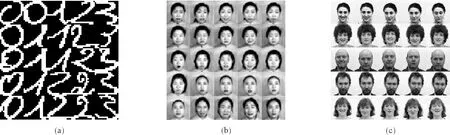
图1 三种数据集(a)Semeion数据集；(b)Jaffe数据集；(c)PIX数据集

3.2 实验评价指标

选用Accuracy(ACC)、Normalized Mutual Information(NMI)、Purity这三种评价指标[17]来衡量图像聚类效果。ACC：对于实例xi，令li,ti分别为聚类所得标签和真实标签其中，n为数据集中实例样本数量；当x=y时，Delta函数δ(x,y)值为1，在其他情况下为0。

(15)

(16)

(17)

Purity：测量每个集群包含主要来自一个类的数据点的程度。聚类解的纯度是作为单个聚类纯度值的加权和，表示为

(18)

(19)

其中，Si是一个大小为ni的特定簇，nij是分给第j个类的第i个输入类的样本数量，K是类数量，n是点总数。一般来说，纯度值越大，聚类结果就越好。

3.3 聚类结果

本文所提算法与其他四种算法在三种数据集上的聚类效果对比见表1～表3。可知，在Jaffe数据集上，本文算法除RMNMF外聚类效果最佳，ACC提高3%～19%，NMI提高1%～18%，Purity提高3%～14%；在Semeion数据集上，本文算法聚类效果最佳，ACC提高2%～10%，NMI和Purity提高4%～15%；在PIX数据集上，本文算法聚类结果也最佳，三种聚类指标都提高3%～18%。同时，新算法在三种数据上的聚类性能比较稳定，其他算法稳定性较差。RMNMF虽然在样本相对简单的Jaffe数据集上聚类结果最佳，优于本文算法，但在其他两种数据集上的聚类效果低于本文算法约10%。这说明实验中不同数据集对会算法效果产生影响，RMNMF算法的聚类效果有较大波动，而本文算法受影响较小。

表1 不同算法的Accuracy对比(%)

表2 不同算法的NMI对比(%)

表3 不同算法的Purity对比(%)

3.4 参数选择

在目标函数求解迭代时，参数取值非常重要，会影响最终的聚类效果。本文算法的目标函数包括2个参数λ和θ。由于新算法是一种无监督算法，不能提前确定最优参数值，因此通过遍历法选择参数。λ的遍历区间设置为{0.001、0.01、0.1、1、10、100、1000}，θ的遍历区间设置为{0、0.1、0.2、…、0.9、1}。为保证实验公平，对比算法中若有相应的约束项参数，也做相同的遍历区间设置。通过实验发现当θ为0.5时效果最佳，当λ等于0.01或0.1时效果最佳。

3.5 收敛性分析

为验证本文所提算法是否具有收敛性，实验记录了不同数据集上迭代过程中的目标函数值，受篇幅所限，仅展示部分迭代过程，如图2所示。在迭代次数达到500次左右时，本文所提的模型已经达到收敛。

图2 目标函数迭代图(a)Jaffe数据集上的迭代图；(b)PIX数据集上的迭代图

4 结论

本文基于非平滑非负矩阵分解算法，提出了一种新算法，在目标函数中加入了核函数和局部相似性约束项来处理非线性数据，弥补了传统非光滑非负矩阵分解未考虑数据间几何结构的局限。针对非凸问题优化求解困难的特点，本文实验优化过程中设计了乘性迭代方法进行迭代求解。新算法在Jaffe、Semeion、PIX三种开源数据集上的聚类效果良好，并能够在迭代过程中达到收敛，验证了该算法的可行性和有效性。下一步研究考虑将新算法扩展至其他应用场景如有噪声的数据聚类领域，优化算法的时间复杂度和收敛速度。