模拟动断裂问题的多尺度扩展有限元方法

张凝,尹硕辉,赵子衡

(湘潭大学 机械工程学院,湖南湘潭 411105)

部件受外部动载荷影响,其内部微观层面的缺陷会出现应力集中现象,以致产生裂纹萌芽、拓展,进而产生宏观层面的裂缝,随着裂缝的增多最终造成整个机构失稳[1],因此动断裂的研究对机构的安全性和稳定性是非常重要。

动断裂裂纹存在不稳定扩展的特性,通过控制和引导裂纹扩展成为了工程中最有效、快速的结构分离模式[2],在结构安全性设计、大型机构产品定期维修、某些材料分割加工等具有很大的实用价值。

研究动断裂裂纹扩展问题,国内外主要采用试验研究和数值理论分析两种手段。试验方面,李清等[3]利用落锤冲击试验以及动焦散线试验方法研究了冲击下预制裂纹梁的动态断裂行为;岳中文等[4-5]利用对岩体和梁进行动态焦散线三点弯曲冲击试验来研究梁和岩体的动断裂行为;杨仁树等[6]利用动态焦散线三点弯曲冲击试验研究裂纹角度对相互贯通裂纹动断裂特性的影响;钟红等[7]利用轴拉试验研究混凝土和花岗岩的动态断裂性能;Sharma[8]利用气枪冲击试验结合人工神经网络分析长径比对颗粒聚合物复合材料动态断裂韧性的影响。

在数值理论研究方面,因动裂纹存在不稳定扩展,而扩展有限元方法因不需要预制裂纹路径优势,广受学术界青睐。Song等[9]分别对扩展有限元方法、单元删除法和界面裂纹法对脆性材料的有限元分析,结果表明XFEM更有优势;Menouillard等[10]利用无网格技术对扩展有限元法进行改进来模拟动断裂问题;Asareh等[11]结合显式时间积分和内聚规律改进扩展有限元法,来预测脆性材料动断裂问题;Zeng等[12]利用嵌入式有限元法和扩展有限元法模拟动态裂纹扩展并与实验作比较;Yin等[13]利用多尺度扩展等几何方法对弹性固体进行静态和动态断裂分析;Teng等[14]在扩展有限元基础上利用自适应网格方法研究微观缺陷对裂纹扩展影响。

工程中动断裂问题数值模拟需要很大的计算量,网格尺度是计算量大的主要成因之一,本文基于此问题提出多尺度扩展有限元法,通过MATLAB进行数值计算,并通过与经典算例数值计算结果进行对比,验证该方法的有效性和可靠性。

1 基本方程

二维裂纹问题示意图如图1所示,边界Γ=Γu∪Γt∪Γc,其中,Γu、Γt、Γc分别为模型的位移边界、应力边界、裂纹面边界。模型所有区域的集合用Ω表示。

图1 二维裂纹问题示意图

动态断裂模型满足以下平衡方程和边界条件:

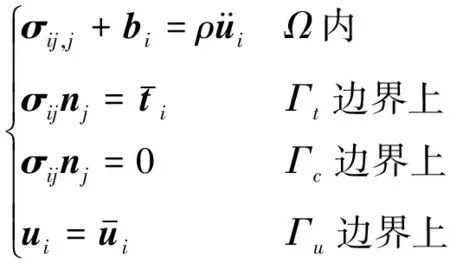
(1)

(2)

模型的本构方程为

(3)

2 多尺度扩展元法

2.1 位移模式

扩展有限元(XFEM)是传统有限元法的扩展,相对于传统有限元法,在求解不连续断裂问题上具有更高的精度和效率[15]。XFEM的动态裂纹的位移模式可表示为

(4)

式中:Ni、Nj、Nk为标准有限元结点形函数;ui为结点位移向量的连续部分;Ω为所有结点的集合;aj、bαk为富集结点变量;Ω1、Ω2分别为Heaviside富集函数和裂尖分支富集函数的结点的集合;H(x)、χα(x)分别为Heaviside函数和裂尖分支函数。Heaviside函数和裂尖分支函数结点分布如图2所示。

图2 裂纹结点分布图

Heaviside函数表达式示为

(5)

式中:x为参考点;x*为裂纹上离参考点x最近的一点;en为在裂纹x*处的外法线单位向量。

裂尖分支函数能反映裂纹尖端附近的奇异性和不连续性,对于二维各向同性的弹性体问题,裂纹分支函数的表达式为

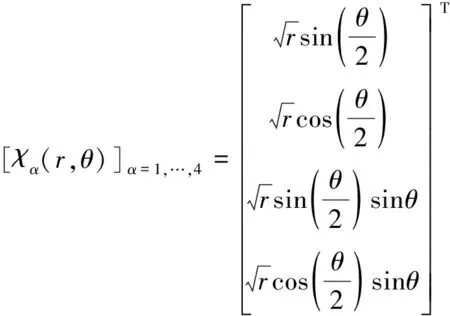
(6)

式中(r,θ)为裂纹尖端局部的极坐标。其中,裂纹分支函数的第一项可反映裂纹面的不连续性,在裂纹尖端附近的裂纹面可表现为断裂;其余3项可改善裂纹尖端奇异性。

2.2 控制方程

在忽略阻尼的影响下,动态断裂的控制方程为

(7)

式中:δ=[u,a,b]T为未知列向量系数;K为整体刚度矩阵;M为质量矩阵以及;R为载荷矩阵。

(8)

式中:i、j为节点编号;u、a、b分别为标准结点、Heaviside函数结点、裂尖分支函数结点对刚度矩阵分量的影响上标。

相应单元质量矩阵元素为:

(9)

(10)

(11)

(12)

(13)

(14)

(15)

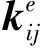
(16)

(17)

(18)

(19)

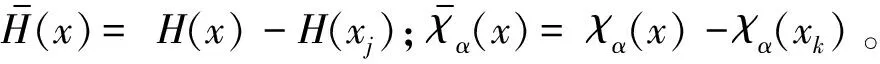
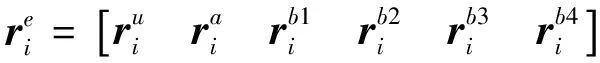
(20)

单位载荷矩阵元素为:

(21)

(22)

(23)

式中:Fb为体力;Fs为面力;F为集中力。

2.3 时间积分方案

控制方程求解方式有隐式积分和显示积分两大类,本文采用隐式积分中的Newmark积分对控制方程时间积分。离散方程在第n个计算步可以表示为[13]:

(24)

式中:α、β为Newmark法参数;Δt为计算时间的步长增量。

2.4 可变结点

计算量与网格规模有关,通过适当的增加单元规模,可以提高计算精度。但同尺度加密网格单元会造成计算量的浪费,因此只针对重要部位采用局部网格加密是更好的方法,如图3所示。

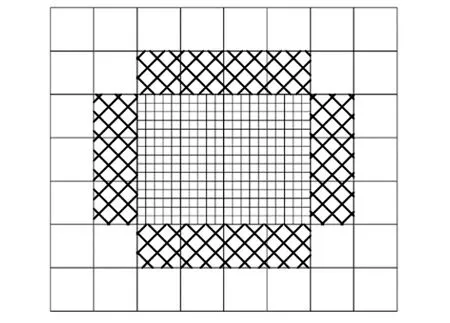
图3 多尺度网格示意图

采用可变结点单元[16]连接不同尺度网格,如图3交叉部分网格单元所示。可变结点单元四周边上的结点数在允许的范围内可以是任意值,如图4所示,虽然结点数增加,但任一两个相邻点的插值特性仍是线性的。

图4 (4+k+l+m+n)结点单元示意图

可变结点的位移模式可表示为

(25)

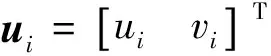
(26)

插值点表示为

uh(ξ)=aTp(ξ)=UTq-1p(ξ)

(27)

式中:q=[p(ξ1),…,p(ξ4+k+l+m+n)];U=[u1,…,u4+k+l+m+n]T。通过联立式(25)与式(27)可以得到

[N1,…,N4+k+l+m+n]T=q-1p(ξ)

(28)

2.5 动应力强度因子

本文计算应力强度因子是利用互作用积分[17]形式推导。因考虑二维裂纹问题,因此裂纹可以用J积分描述,如图5所示,用一条周线Γ0围绕裂尖。

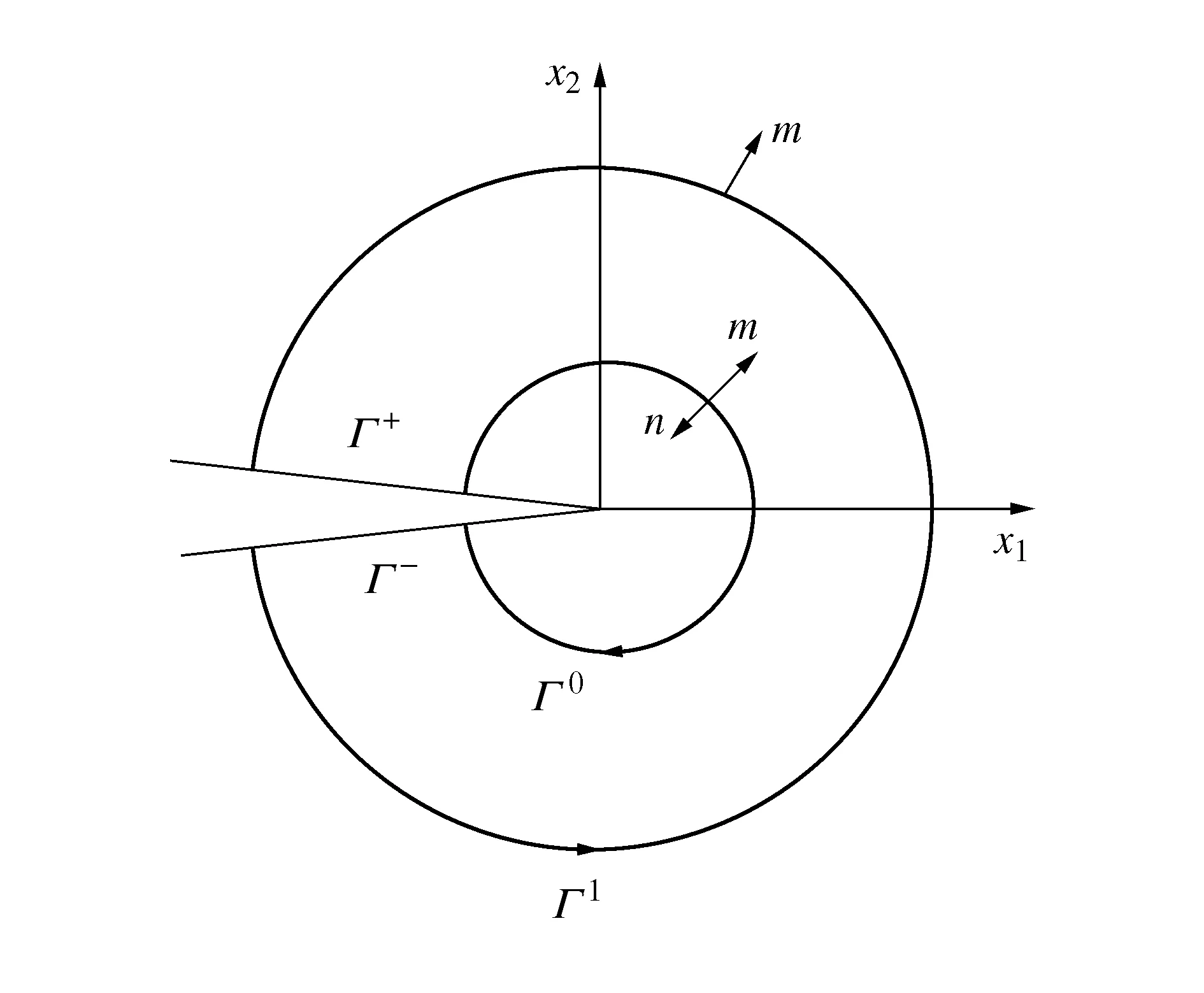
图5 J积分轮廓图

利用散度定理,并将平衡方程和几何方程代入,可以得到J积分表达式[18]为

(29)

J(1,2)=J(1)+J(2)+I(1,2)

(30)

互作用积分I(1,2)为

(31)

(32)

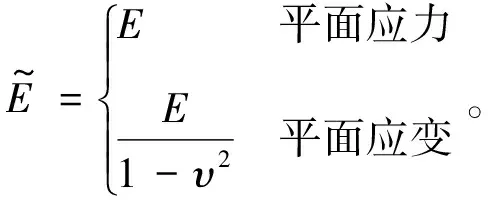
因此,第三平衡状态可以改写成

(33)

通过式(30)与式(33)可以得到

(34)

令平衡状态2为Ⅰ型和Ⅱ型的渐近场,可以得到

(35)

3 数值算例

3.1 算例1:半无限板Ⅰ型裂纹动态断裂

研究半无限板上Ⅰ型裂纹在拉力作用下的动裂纹扩展。如图6所示,在半无限板选取L×2H=10×4 m有限区域为研究对象,裂纹长度a=5 m。板的弹性模量E=210 GPa,泊松比ν=0.3,密度ρ=8 000 kg/m3。有限区域顶端受到一分布载荷σ0=1 500 MPa,为避免应力波影响,计算时间为t=1×10-3s≤3tc=H/cd=1.009×10-3s[18],其中,cd为应力波的传播速度,tc为应力波第一次到达裂尖的时间。

图6 Ⅰ型裂纹计算模型示意图

为了方便比较,将动应力强度因子归一化,在不考虑裂纹扩展的情况下半无限板Ⅰ型裂纹动态应力强度因子计算公式为[19]

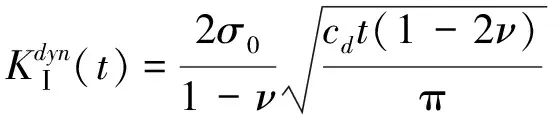
(36)

定义归一化动态应力强度因子的相对误差为

(37)

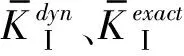
3.1.1 数值算例验证与比较

为验证多尺度扩展有限元方法的优劣性,分别对算例的解析解、标准扩展有限元法以及多尺度扩展有限元法的数值解作比较,并计算相对误差,如图7和图8所示。

图7 不同方法归一化动强度因子结果比较

图8 不同方法归一化动强度因子结果比较

数值计算中的网格模型分为65×25、多尺度网格、79×41、195×75这4种,如图9所示。

图9 半无限板网格示意图

多尺度网格模型是由原始网格模型65×25中的裂纹附近网格进行3×3细化,共3 239个网格单元,计算自由度为6 812。与之作比较的网格单元规模为65×25(自由度3 592)、79×41(自由度6 908)、195×75(自由度30 212),对应优化比较、同等自由度比较、同等细网格尺寸比较。

从图7和图8可以看出多尺度扩展有限元法数值解与同等细网格尺寸下的标准扩展有限元法数值解能很好的吻合解析解,但同等自由度下的标准扩展有限元法精度没有多尺度扩展有限元法精度高。结果表明,多尺度扩展有限元法比标准扩展有限元法有更高精度。

3.1.2 计算效率

如表1所示,对各个模型进行计算所消耗的时间进行记录比较,可以看出,多尺度扩展有限元法比195×75网格模型的标准扩展有限元法计算的时间短很多,即在得到相似精度数值解情况下,多尺度扩展有限元法相较于标准扩展元法计算效率提高188%左右。

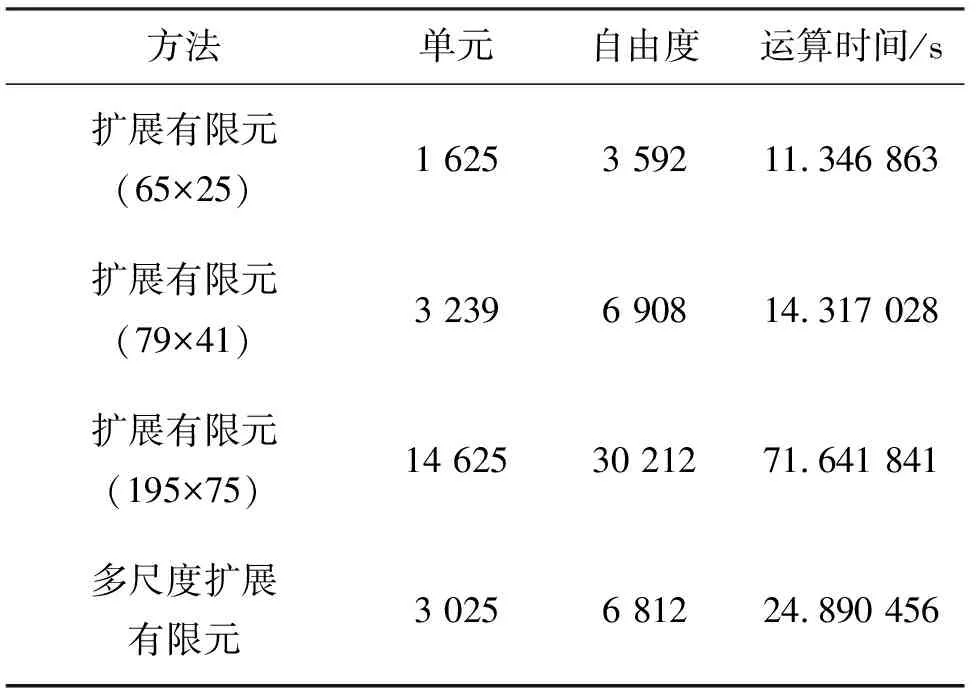
表1 算例运算时间记录表

3.2 算例2:边界斜裂纹板动断裂

为验证混合裂纹模式下多尺度扩展有限元法的适用性和可靠性,如图10所示,对带有斜裂纹的矩形板进行计算。

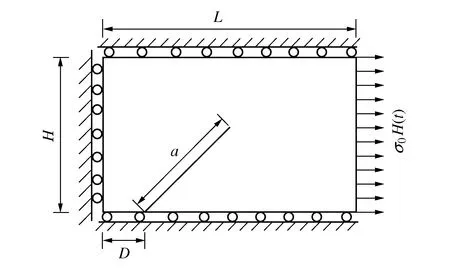
图10 边界斜裂纹板示意图

板的几何尺寸L×H=44 mm×32 mm,裂纹距离左边界的距离D=16 mm,裂纹长度a=22.63 mm,与下边界的角度成45°锐角。板的弹性模量E=29.4 GPa,泊松比ν=0.286,密度ρ=2 450 kg/m3。右边界受一均布拉伸冲击载荷σ0H(t),其中H(t)为Heaviside阶跃函数,板的上、左、下边界受法向位移约束。设定计算时间为3×10-5s。

网格划分如图11所示,用于标准扩展有限元法数值计算的网格模型为45×21;用于多尺度扩展有限元法数值计算网格模型如图11b)所示,原始网格模型为15×7,裂纹附近采用3×3网格细化。

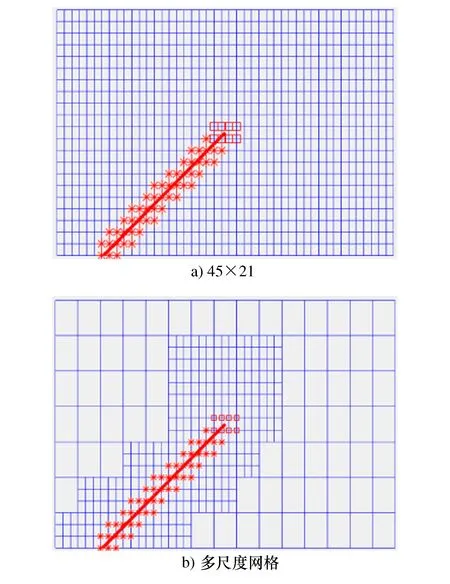
图11 边界斜裂纹板网格示意图

采用同等细网格比较,通过数值计算验证多尺度扩展有限元的实用性和可靠性,计算结果如图12所示。

图12 不同方法归一化动强度因子结果比较

从图12可看出,标准扩展有限元法和多尺度扩展有限元法两种不同方法计算出来的数值解吻合较好,表明多尺度扩展有限元也适用于分析混合裂纹模式的动裂纹扩展。

4 结论

通过给出多尺度扩展有限元数值计算结果与解析解、不同网格模型的标准扩展有限元数值计算结果进行对比。结果表明:

1) 多尺度扩展有限元数值计算结果与解析解及标准扩展有限元数值计算结果一致。

2) 多尺度有限元法比标准扩展有限元法具有更高的精度和更低的计算成本。

3) 多尺度扩展有限元法适用于混合裂纹下动断裂裂纹扩展。