鸵鸟足型沙地履带板设计及牵引性能研究
干霖杰,黄青青,陈劭
(北京林业大学 工学院,北京 100083)
履带式行走机构具有接地比压小、附着性能好、牵引效率高、结构简单和控制便捷等显著优点,可应用在沙地作业机械上,完成沙地资源的勘探、开采、运输等任务。而履带板是作业机械与地面接触的关键零部件,起到传递机械与地面间相互作用力、力矩等作用,其结构形式直接影响着牵引性能。
常规作业机械在松软沙地上极易出现滑转下陷、甚至无法行进等问题[1-2],主要原因是沙土在载荷作用下出现明显的塑性变形并迅速扩展,且破坏后沿侧向和纵向流动。研究人员基于工程仿生技术,设计并优化了一系列仿生行走机构,主要包括轮式、腿式及复合式等[3-5]。这些仿生行走机构均可在一定程度上提高作业机械的软地通过能力,但在流动性更大、地形较为规则沙地上依旧存在一些缺陷。例如,相比于履带式行走机构,轮式行走机构在松软沙地行驶时下陷量更大,通过能力受到轮胎尺寸的制约;腿式及复合式等行走机构虽具有良好机动性和越障能力,更适用于复杂多变的非规则地面(具有壕沟、崖壁等),但存在结构和控制系统较复杂等问题。现有多数履带板是针对在矿山、泥地、雪地、沼泽等地面而设计的,并不适合在沙地上使用。所以,有必要针对在松软沙地上使用的履带板进行设计与研究。
文献[6-8]基于车辆地面力学、土力学等理论建立了履带板-土壤相互作用的力学模型,研究不同结构参数对牵引性能的影响;文献[9-11]则采用土槽实验或田间实验等进行研究。理论分析得到的解往往是基于对土体力学行为、边界条件等诸多简化与假设所得,与实际情况存在一定差异;而实验方法往往受到成本、时间等条件的制约。随着计算方法及计算机技术的发展,有限元法已在轮/履带板-地面相互作用的研究中得到广泛运用[12-13]。有限元法可快速便捷地研究不同行驶条件、地面土壤参数、履带板结构参数等因素对牵引性能的影响。
本文根据车辆地面力学理论及鸵鸟足的越沙机理,在现有某款履带板的基础上设计一款鸵鸟足型沙地履带板,并建立履带板-沙地牵引力数学模型;采用有限元方法对履带在沙地上的运动模拟,分析履带板的不同参数对牵引性能的影响;最后试制出优选的沙地履带板,进行实际沙地牵引实验。
1 鸵鸟足型沙地履带板设计
鸵鸟在沙地中的高速奔跑能力与其特殊的足部结构有关,如图1所示,鸵鸟足仅有第Ⅲ趾和第Ⅳ趾。其中,第Ⅲ趾较发达,前端有坚硬的趾甲;第Ⅳ趾较小,前端趾甲较小甚至退化;两趾底部均有典型的曲面形貌,可分为第Ⅲ趾前掌缓曲面、中间凹槽面、后掌缓曲面以及第Ⅳ趾底曲面。

图1 鸵鸟足底部形貌
文献[14]研究表明,当鸵鸟行走或奔跑时,趾甲扎入沙土中可增大牵引力,底部曲面形成的空腔有助于固沙限流。
将鸵鸟足底部形貌与履带板相结合,本研究设计的鸵鸟足型沙地履带板如图2所示。

图2 鸵鸟足型沙地履带板
该履带板采用金属铸焊一体式,分为主体板与履刺板两部分。相比于同等尺寸的全铸造式履带板,该形式具有质量轻、功耗小等显著优点。主体板采用整体铸造式,其与驱动轮、导向轮、支重轮等相互配合,主要起到传递车辆与地面相互作用力的作用。
履刺板焊接在主体板上,其底部形式如图3所示,履刺分为横履刺和斜履刺。横履刺相当于鸵鸟足趾甲,可扎入沙土增大牵引力;两种履刺与板体构成的半封闭式空腔相当于鸵鸟足底部曲面形成的空腔。当车辆行驶时,沙土相对于履带运动方向作反向流动,沙土流动受到履刺的限制并逐渐聚集在半封闭式空腔内;当沙土聚集到一定程度(履带不再滑转)时,沙地对履带接地段的反作用力可推动车辆行驶。即该种形式的履带板可限制沙土塑性流动,提高沙地通过性。

图3 鸵鸟足型沙地履带板底部形式
履带板的基本设计参数包括履带节距l、履带板宽度b等。履带节距l计算式为

(1)
式中G为沙地作业机械的总重量,G=50 000 N。
履带板宽度b计算式为

(2)
式中:p为接地比压力,一般的履带车辆在松软地面上具有良好通过性时,其接地比压力不超过50 kPa;L为履带接地长度。
2 单块履带板牵引性能分析
本文以鸵鸟足型沙地履带板的结构参数为研究对象,采用理论分析及有限元仿真分析结合的方法,研究结构参数对牵引性能的影响。
2.1 单块履带板理论分析
通常用牵引力来评价牵引特性,而地面牵引力与地面剪切力是一对相互作用力[15],因此地面剪切力可作为牵引特性的评价指标。地面剪切力是指,履带板在剪切沙土的过程中受到的反作用力(与剪切运动方向相反),它既与沙土力学参数相关,又与履带板的结构参数相关。文献[7-8]中指出履带板在剪切过程受到的反作用力通常可分为以下4部分:作用在履带板底部的力F1,作用在履刺底部的力F2,作用在履刺上的力F3以及作用在履带板及履刺两侧的力F4。F1、F2和F4计算式[7-8]分别为:
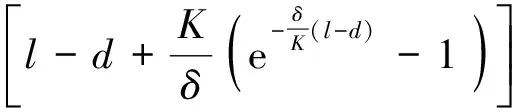
(3)
(4)

(5)
式中:b=460~660 mm;沙土黏聚系数c=13.79 kPa;沙土内聚力变形模量kc=2.79 kN/mn+1;沙土内摩擦变形模量kφ=141.1 kN/mn+2;沙土压缩变形量z=60~100 mm;沙土变形指数n=1.15;l=120 mm;履带板厚度d=7 mm;沙土水平剪切变形模量K=2.5 cm;滑移率δ=5%~20%;履刺高度h=60~100 mm;沙土内摩擦角φ=27.5°。
建立F3数学模型,需要结合该沙地履带板的履刺具体形式。新设计的履带板底部履刺如图4所示,单块履带板包括1个横履刺及N个斜履刺,横履刺与斜履刺之间的夹角α∈[45°,75°],b1为斜履刺在横向上的投影长度。

图4 履带板底部履刺简化示意图
F3的计算涉及到土压力理论,在车辆地面力学中的土压力属于被动土压力,一般采用Rankine土压力理论进行研究。经典的Rankine被动土压力可表示为

(6)

单块履带板的接地压力可视为均匀分布,如图5所示。

图5 均布载荷-履刺剪切作用下沙土破坏模型
因此在均布载荷p作用下,横履刺上产生的附加力为
(7)
式中均布载荷p=35 kPa。
而单个斜履刺产生的附加力为
(8)
式中斜履刺横向投影长度b1=40 mm。
该种形式履带板的斜刺个数为N,因此沙土作用在履刺上的力F3为
F3=F31+NF32
(9)
式中斜刺个数N分别为2和4。
综上所述,可得单块履带板在沙地上的地面剪切力表达式为
FS=F1+F2+F3+F4
(10)
2.2 单块履带板仿真分析
土是由土颗粒、孔隙气和水组成的三相材料。从微观角度来看,土壤颗粒之间存在空气和水分等,使得土壤介质不连续;但在大多数实际应用中,土被理想化为连续体,“微观”作用被均匀化,即宏观上把土材料视为连续介质或固体材料。因此,土在载荷下的力学性质,即土的应力应变关系,可用弹塑性本构模型进行描述。
履带板在沙地上的运动是一个高度非线性弹塑性问题。针对这类非线性和大变形问题,采用耦合欧拉-拉格朗日法(Coupled Eulerian-Lagrangian,CEL),即用拉格朗日网格描述履带板,欧拉网格描述土体,这样可以有效解决土体网格的大变形扭曲畸变的问题,并能精确地确定运动界面的位置。
在仿真中,履带板的运动简化为向下沉陷和剪切运动。选择履带板宽度b=560 mm、履刺高度h=80 mm、履刺夹角α=60°、斜履刺个数N=2、剪切速度为100 mm/s的履带板作为基准履带板,并将该履带板简化为图6所示形式。

图6 简化履带板
将沙地简化为3 000 mm×2 000 mm×1 300 mm的土体,土体单元采用EC3D8R;土的本构模型采用各向同性弹性模型和Mohr-Coulomb模型,相关参数见表1。如图7a)所示,土体可分为欧拉材料区和欧拉空隙区,材料区是初始时刻土体所占有的区域,空隙区用来容纳仿真过程中的土体材料的运动及变形。综合考虑结果的准确性及计算效率,整个土体采取中间致密四周稀疏的分区域网格划分方法,最终仿真模型(隐藏欧拉空隙区)如图7b)所示。仿真输出变量设置为:履带板在剪切沙土过程中,接触面所受到的所有反作用力(与剪切方向相反),即沙地剪切力(牵引力)。

图7 有限元模型
图8是该基准履带板-沙地仿真在不同时刻沙土的变形。t0时刻为初始时刻,t0-t1时间段履带板竖直向下压实沙土,履带板四周沙土微微隆起;t1-t2时间段履带板沿x轴正向剪切沙土,被剪切的沙土在履带板前方不断堆积并逐渐升起,形成如图所示的壅土区,该现象与实际情况相符。

图8 不同时刻沙土变形
图9包含两条关系曲线:1) 该基准履带板-沙地仿真中t1-t2时间段剪切力随剪切位移的关系曲线;2) 同等条件下,由式(10)计算得到的理论关系曲线。从图9中可以看出,仿真计算结果与理论计算结果具有较好的一致性,且单块基准履带板所受到的剪切力FS≈2 800 N。

图9 剪切力-剪切位移关系曲线
为研究不同的履带板参数对地面牵引力的影响,考察的因素有履带板宽度(A)、履刺高度(B)、履刺夹角(C)、斜履刺个数(D)、剪切速度(E),考察的实验指标是剪切力(与地面牵引力构成相互作用力),确定的因素水平表如表1所示。

表1 因素水平表
本研究采用正交实验分析,选取常用的正交表L18(36×6)安排正交实验:将因素D虚拟一个水平3(值与水平1相同);设置了空白列,用来衡量实验的可靠程度,提高分析的可靠性。实验方案及结果如表2所示。
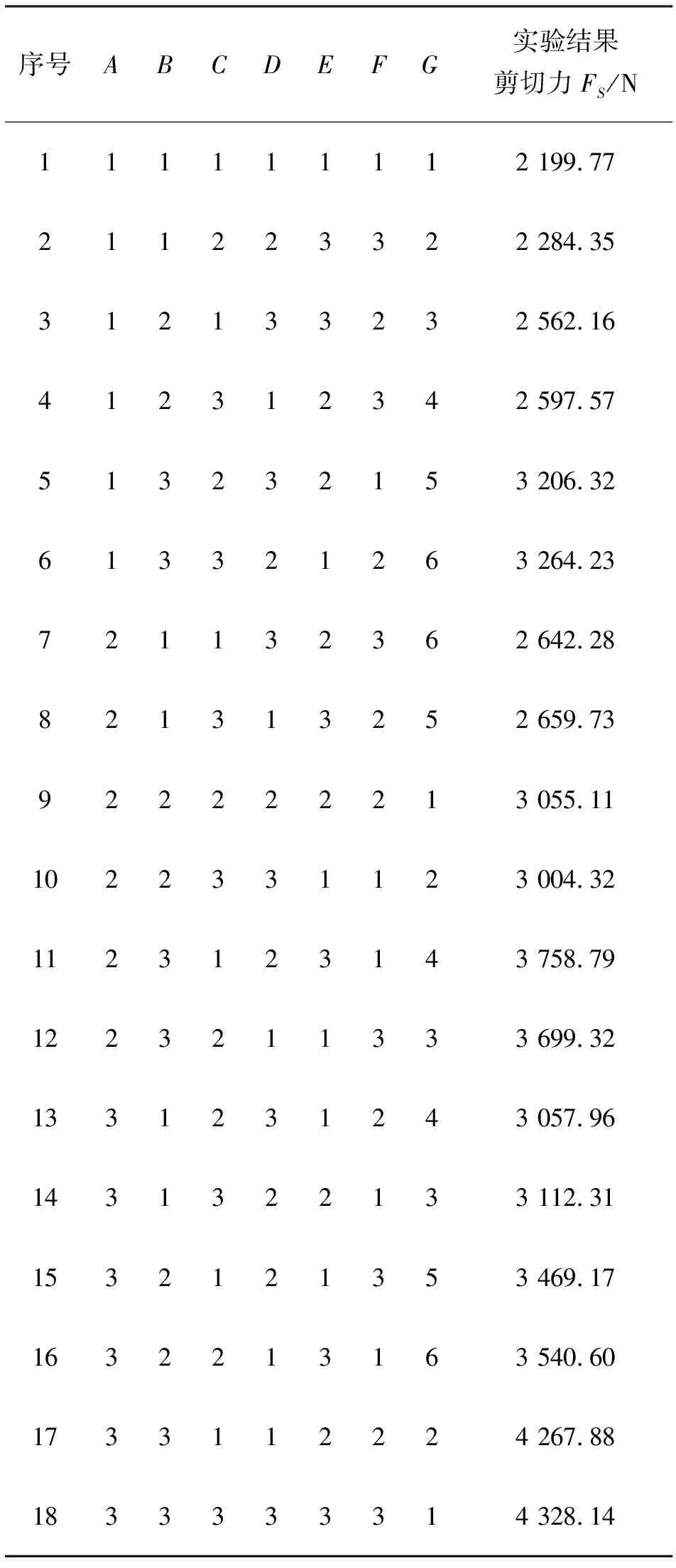
表2 实验方案及实验结果表
2.3 数据处理及结果分析
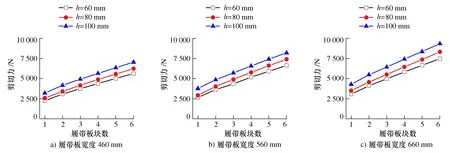
根据上述正交实验,可得出方差分析如表3所示。从表中可以看出,鉴于因素C和因素D的均方值均小于两倍的误差均方值(MSC<2MSe、MSD<2MSe),可认为C、D的水平改变对实验结果几乎无影响,因此可将两者并入误差项e中,作为新的误差项e;FA>F0.01(2,11),FB>F0.01(2,11),说明因素A、B水平的改变对实验结果具有高度显著的影响,记为**;而FE 表3 方差分析表 因此,可知履带板宽度及履刺高度对沙地牵引力的影响最为显著,而履刺夹角、斜履刺个数以及剪切速度对其基本无影响。若将显著因素作为自变量,其余因素取值与基准履带板参数相同,式(10)理论模型可转化为图10所示的三维曲面。由图10可知,剪切力与履带板宽度、履刺高度均呈现正相关性。 图10 显著因素对剪切力的影响 为探讨履带板受到的剪切力与块数之间的关系,进行多块履带板的仿真分析。从经济成本、制造加工、履带重量及动载冲击等角度考虑,将非显著因素直接设置为:履刺夹角α=60°,斜履刺个数N=2,剪切速度100 mm/s。因此,实验研究的变量为履带板宽度b分别为460 mm、560 mm、660 mm、履刺高度h分别为60 mm、80 mm、100 mm及履带板块数分别为1、2、3、4、5、6,实验输出结果为履带板与沙土接触面所受到的所有反作用力(与剪切方向相反),共计3×3×6=54组实验。 以两块履带板为例,其简化模型如图11所示,其余块数履带板简化模型与之类似。 图11 简化履带板(2块) 整理数据,最终可得到图12所示结果。从图12中可以看出,即使履带板的形式不同,但是剪切力都是随着履带板的块数增加而增大;每增加一块履带板,其剪切力的增幅大约为单块履带板受力的30%(增幅η≈30%)。 图12 不同形式履带板剪切力与履带板块数关系 因此,可外推出整车在沙地上的受力为 (11) 式中C为履带车的履带数。 为验证该鸵鸟足型沙地履带板的实用能力,以及研究两显著因素对牵引力的实际影响,进行实际沙地牵引实验。实验场地选择在黑龙江省大庆市杜尔伯特蒙古自治县(46°29′12″N,123°56′43″E,海拔140 m)的沙地(沙土密度ρ=1 540 kg/m3;沙土杨氏模量E=20.2 MPa;沙土泊松比μ=0.25)上进行。实验车的总质量G=50 000 N,履带条数C=2,履带接地长度L=1 600 mm,履带节距l=120 mm。 如图13、图14所示,在沙地上用该履带实验车牵引一履带式负荷车(要求其整车质量大于实验车质量),拉力传感器通过钢丝绳连接在两车之间;逐渐增大负荷车的制动程度,使实验车产生最大牵引力。 图13 实际沙地牵引实验方案 图14 实际沙地牵引实验 实验车分别安装如表4所示的五种型号履带板进行多次牵引实验,将实验测得的数值取平均值(剔除误差较大项后)作为整车牵引力。 表4 沙地实验履带板及实验结果 实验表明,新设计的鸵鸟足型沙地履带板能保证整车在沙地上正常行驶。分析1号、2号和3号履带板的实验结果,可知履刺高度越高,整车牵引力越大;分析1号、4号和5号履带板的实验结果,可知履带板宽度越宽,整车牵引力越大;这与上述理论结果及仿真结果基本一致。 考虑到履带板的尺寸参数越大,其运行过程中的噪声、能量消耗、动载冲击等也就越大,同时过大的履带板会导致整车运行缓慢、转向困难等问题。结合现场实验情况,优选出1号履带板作为基准。 图15中的散点是1号基准履带板的沙地实验结果,虚线表示由式(10)计算得到的理论值。9次实验中有2次实验数据与理论值存在明显误差,产生误差的原因可能是:1) 实际沙地不是理想的完全均匀体;2) 车体短暂非匀速行驶时的冲击造成。 图15 “1”号履带板沙地实验结果 本研究基于车辆地面力学理论及鸵鸟足越沙机理,设计了一款适用于沙地的履带板;通过对履带板在沙地运动上的理论、仿真及实验研究,分析了履带板参数对牵引性能的影响,得到如下结论: 1) 履带板在沙地上的运动可用沉陷及剪切运动简化,仿真计算结果与理论计算结果具有较好的一致性,由多块履带板有限元仿真结果外推得到的整车牵引力与实际沙地牵引实验的结果也较为接近,说明建立的履带板-沙地的理论数学模型、有限元仿真模型基本正确,能较好的预测履带板的结构参数对牵引特性的影响。 2) 针对该种形式的沙地履带板,履带板宽度及履刺高度对其牵引性能影响最为显著且呈现正相关性,而履刺夹角、斜履刺个数以及剪切速度对其基本无影响。 3) 单块基准履带板在该种沙地上运动时,牵引力约为2 800 N;每增加一块履带板,其牵引力的增幅约为单块履带板受力的30%,而装有基准履带板的实验车在该沙地行驶时的地面牵引力约为30 kN。

3 多块履带板仿真及沙地牵引实验
3.1 多块履带板仿真分析

3.2 实际沙地牵引实验分析




4 结论

