融合信息增益与基尼指数的决策树算法

谢 鑫，张贤勇，杨霁琳

1.四川师范大学 数学科学学院，成都 610066 2.四川师范大学 智能信息与量子信息研究所，成都 610066 3.四川师范大学 计算机科学学院，成都 610066

大数据时代需求高效的信息获取，这对数据分类及相关知识发现提出了更高要求。数据分类的方法主要有贝叶斯分类、神经网络、支持向量机、决策树等。其中，决策树是机器学习与数据挖掘的一种基本分类策略，在决策支持、信息分析、医疗诊断等方面具有广泛的研究与应用[1-3]。决策树自1966年提出，而后主要关注结点选择来进行决策树构造、改进、优化。现有决策树算法的节点度量函数选择，具有偏向于信息熵、基尼指数、粗糙集理论三个方向。ID3（iterative dichotomiser 3）

算法[4]、C4.5算法[5]及其改进算法[6-7]选择信息增益或信息增益率。CART（classification and regression tree）算法[8]及其改进算法[9-11]选择基尼指数作为度量函数。例如，文献[9]采用递增式学习来改进CART算法，文献[10]引入模糊逻辑来构建模糊CART算法，文献[11]采用Fayyad边界点与关键度量来改进CART算法，文献[12]依托基尼指数来构建一种模型决策树加速算法。借助粗糙集理论，RS（rough set）算法及其改进算法主要优先考虑属性依赖度[13-14]。

信息增益与基尼指数可以表征数据的不确定性程度或杂乱度，从而对应的ID3算法与CART算法完成决策树基本构建，但相关的分类效果还值得改进。信息熵和基尼指数具有相似的不确定性度量功能，但具有不同的表现形态与测量重点。信息熵侧重于信息表示，对较乱数据具有更强表现力；基尼指数则侧重于代数表示，更擅长较纯集合分类。由此，两种度量的深入结合具有意义，相关融合度量可望获取优化决策树算法，但是相关报告较少；文献[15]将基尼系数关联阈值来构建改进ID3算法，文献[16]采用常数权重来进行线性组合集成。本文将信息增益和基尼指数进行自适应加权集成，产生具有更完备不确定性刻画的融合度量IgGi，再自然构建对应决策树算法IGGI（information gain and Gini index），适用于信息增益和基尼指数都不占绝对优势的应用环境；最后，进行UCI数据实验，对比ID3算法与CART算法来验证IGGI算法的有效性与改进性。

1 两种基本决策树算法

给定一个决策系统DT=(U,C⋃D,{v c|c∈C},{I c|c∈C}),其中U={x1,x2,…,x||U}表示有限样本集，C={c1,c2,…,c|C|}表示条件属性集，D表示决策属性集，V c表示c∈C的属性值域，I c:U→vc是将对象x在属性c上赋值I c(x)的信息函数。为方便，这种决策系统也简记为决策表DT=(U,C⋃D)。相关的监督学习需要涉及条件部分与决策部分的两种粒化（设条件属性子集A⊆C）：

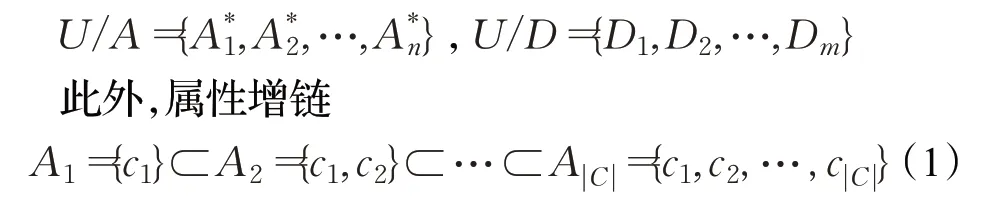
常用于探寻知识粒度层次的规律，如不确定性度量的粒化单调性[17]。

1.1 基于信息增益的ID3算法

来源于信息理论的信息熵关联于系统信息含量，能够表征样本集合的不确定性，由此可以得到经典的决策树归纳算法ID3[4]。

定义1[4]在决策表DT=(U,C⋃D)中，决策分类U/D的信息熵为：

ID3算法遍历每一个属性特征，选择具有最优信息增益的特征来划分数据，由此递归构造决策树。ID3算法操作简单，但容易导致偏移性与低精度，后续具有较多改进算法，包括C4.5算法等。

1.2 基于基尼指数的CART算法

来源于经济统计的基尼（Gini）指数关联于数据杂乱度，相关CART算法可以构造分类树[8]。

定义2[8]在决策表DT=(U,C⋃D)中，决策分类U/D的基尼指数为：

CART算法采用基尼指数来实施属性优选，由此建立分类树。此外，CART算法还可以构建回归树。

2 基于信息增益与基尼指数融合度量的决策树算法

基于上述ID3算法与CART算法，信息增益与基尼指数都适用于决策树构造。下面挖掘它们的一种深入融合度量，进而建立一个强健的决策树算法IGGI，最后采用一个决策表实例来澄清相关的机制与比较。

2.1 信息增益与基尼指数的融合度量

信息增益与基尼指数都是可以用于决策树构造的基本不确定性度量。对于决策树归纳，信息增益侧重于信息表示，对较乱数据具有更强表现力；对比地，基尼指数强调代数表示，更擅长较纯数据的分类处理。可见，信息增益与基尼指数具有异质无关性，两者的融合度量可以系统集成两者优点，从而建立更强健的决策树算法。下面采用加权线性组合来构建融合度量，其中的信息增益粒化单调性是已有的，而其他度量的粒化非单调论断都能够通过实例或实验来有效验证。

引理1信息增益具有粒化单增性，而基尼指数具有粒化非单增性，即：

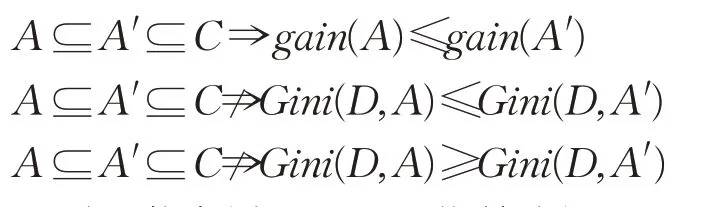
命题1信息增益与基尼指数线性无关，即：

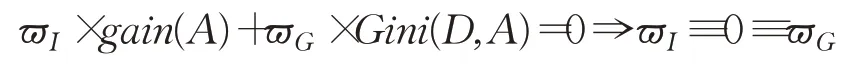
基于引理1，信息增益与基尼指数分别具有粒化单调性与粒化非单调性，相关结果将由后续数据实验中的属性增链来观测。从而命题1表明，信息增益和基尼指数具有线性无关性，该基本结论也会由实验佐证。进而，利用线性组合构建信息增益和基尼指数的融合度量是可行的、有意义的。

定义3在决策表DT=(U,C⋃D)中，D关于A⊆C的信息增益与基尼指数的融合度量（记为IgGi）定义为：

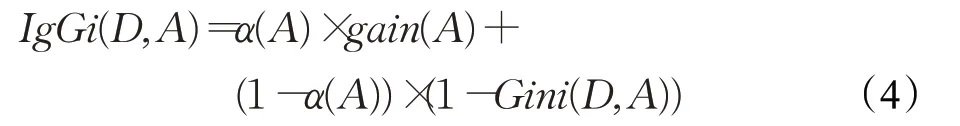
其中α(A)=||U/A/ ||U为基于条件A或知识U/A的自适应系数。

命题2融合度量IgGi具有粒化非单增性，即：

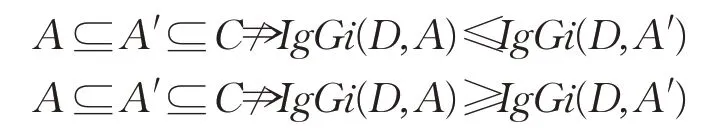
定义3构建了融合度量IgGi。观测式（4），gain(A)与1-Gini(D,A)具有表征属性集A重要性的相同方向，它们的加权系数采用了关联于知识U/A的自适应系数（自适应系数比常系数更易提升分类业绩）。融合度量IgGi深入集成了信息增益与基尼指数，知识粒度系数α(A)起着权重调节功能，通过设置双系数和为1来取得常规范围[0,1]。显然，IgGi随着信息增益增大而增大，随着基尼指数减少而增大。基于命题2，该线性集成度量具有粒化非单调性，该结论来源于引理1与定义3，并将由后续实验反映。总之，基于信息增益与基尼指数的融合度量综合了不确定性的信息表示与代数表示，能够表征属性特征分类纯性的重要功能，适用于更加宽泛数据的分类问题，下面将由此建立决策树新算法。为此，聚焦单属性A={c}，并使用简单符号gain(c)、Gini(D,c)、α(c)、IgGi(D,c)；此外，设arg表述度量m最值的属性反演作用，即∀c∈arg(·)⊆C有m(c)取得最值。

命题3设c1,c2∈C′⊆C，若α(c1)=α(c2)，则

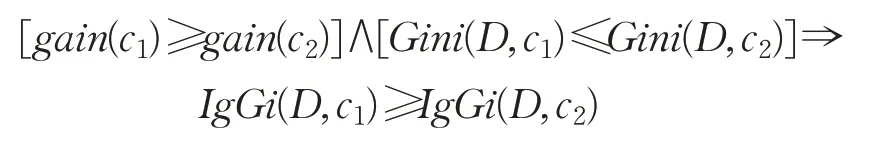
基于定义3与命题3，更大信息增益与更小基尼指数的属性具有取得更大融合度量值的倾向或可能。属性优化关联的一般结论是，信息增益的最大实现与基尼指数的最小实现没有必然联系，两者中的单个最值或同时最值与混合度量最大值也没有必然联系。由此可见，信息增益与基尼指数对决策树构造有所不同，而两者的融合度量对决策树构造具有有效性。

2.2 决策树算法IGGI

基于上述混合度量，下面自然建立相关的决策树算法（简称IGGI算法），主要利用IgGi混合度量进行特征选择，具体描述如下。

算法决策树算法IGGI

输入：决策表DT=(U,C⋃D)。

输出：决策树。

步骤1遍历相关决策树所有属性（设涉及属性范围为C′⊆C），计算相关混合度量值IgGi(D,c),∀c∈C′。

步骤4对于多个子决策表DT1,DT2,…,DT n(c′)，递归地执行上面步骤1~3，直到所有条件粒属于同一决策类或者所有条件属性被检测完。

步骤5返回决策树。

这里，算法IGGI主要采用融合度量IgGi作为决策树构造节点选择的度量函数。具体地，步骤1循环计算所有混合度量值，步骤2确定最优属性特征，步骤3依托优选属性节点进行决策表与决策树的分裂，步骤4实施决策树生成的递归归纳，步骤5最终返回决策树。考虑关联于 ||C的IgGi基本运算，步骤1~2最多涉及时间计算量2 ||C与空间存储量|C|，再加上步骤3~4涉及的上界 ||U，该算法的时间复杂性与空间复杂性的渐进分析为Ο(||C||U)，因此该算法是可行的。显然，IGGI算法具有类似于ID3算法与CART算法的框架，但是采用了更加强健的混合度量（其具有更强的不确定性表示能力），故其意味着更好的决策树分类业绩，相关的优越性将被最后的数据实验所体现与验证。

2.3 决策表实例分析

这里提供一个决策表实例来说明上述决策树算法IGGI。决策表如表1，具有13个样本、5个条件属性、1个决策属性，决策属性具有2类。

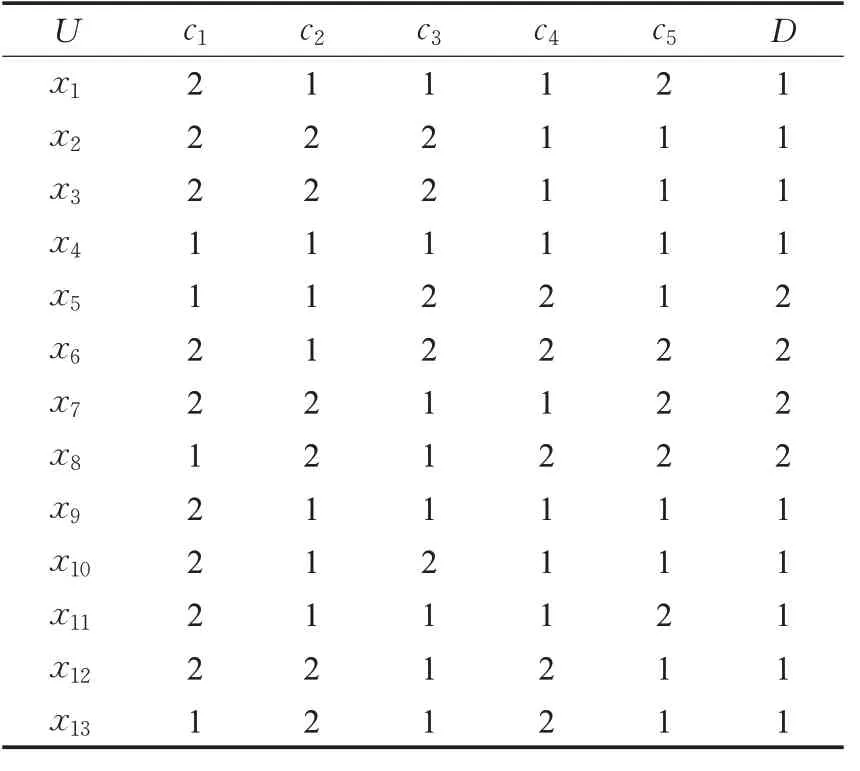
表1 决策表Table 1 Decision table

首先聚焦三种度量及其关系，为此采用式（1）的属性增链进行度量计算，表2与图1（其中α(A k)表示关联于知识粒度的自适应系数）将同时提供信息增益、基尼指数、混合度量的结果。由此，可以部分验证引理1与命题1、命题2，例如信息增益的粒化单调性、信息增益与基尼指数的线性独立性等。

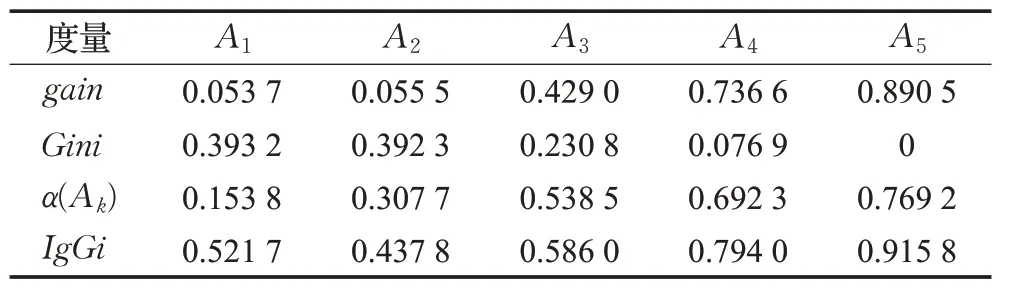
表2 基于属性增链的三种度量值（实例）Table 2 Three kinds of measure values based on attribute-increase chain（Example）

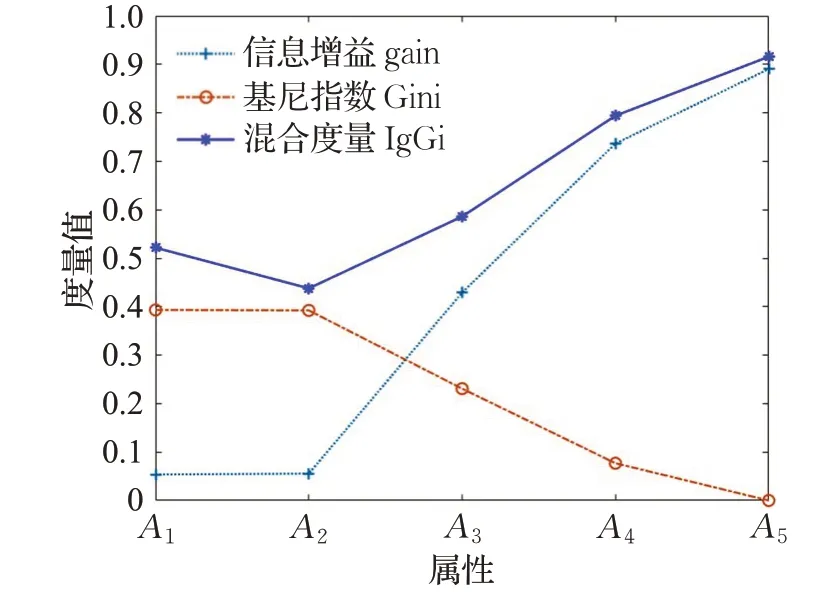
图1 基于属性增链的三种度量变化（实例）Fig.1 Three kinds of measure changes based on attribute-increase chain（Example）

下面展现算法IGGI的实施过程，并给出具体的决策树构造与结果。对于决策表1，需要计算所有单属性的混合度量值IgGi(D,ck)(k=1,2,3,4,5)，相关的过程与结果参见表3。

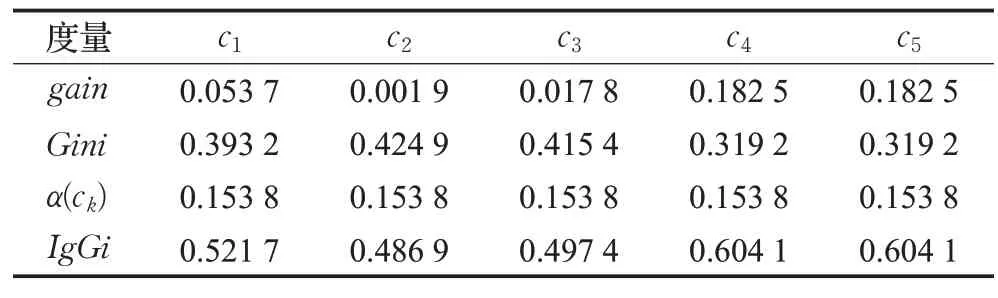
表3 基于单属性序列的三种度量值（实例）Table 3 Three kinds of measure values based on single-attribute sequence（Example）

基于表3可见，三种度量都是在c4、c5处取得最优值，该结果验证了命题3。关于算法IGGI，步骤2将选取一个混合度量最优值节点，设为c5。步骤3是建立c5为根节点，进行决策表分裂。具体地，U/{c5}具有两个类：{x2,x3,x4,x5,x9,x10,x12,x13}、{x1,x6,x7,x8,x11}，它们分别是标签为1的8元集与标签为2的5元集。由此，原来的决策表将分为两个具有4属性的子表（均不含属性c5），分别具有8元与5元。步骤4将对这两个子表递归地进行上述属性优选与决策表分裂过程。步骤5最终给出相关的决策树，如图2其具有4层6个叶子。事实上，算法ID3与CART也会得到相同的结果。相关分析说明了算法IGGI的有效性，其对比于已有两种算法的差异性与改进性将在下述数据实验中深入展现。

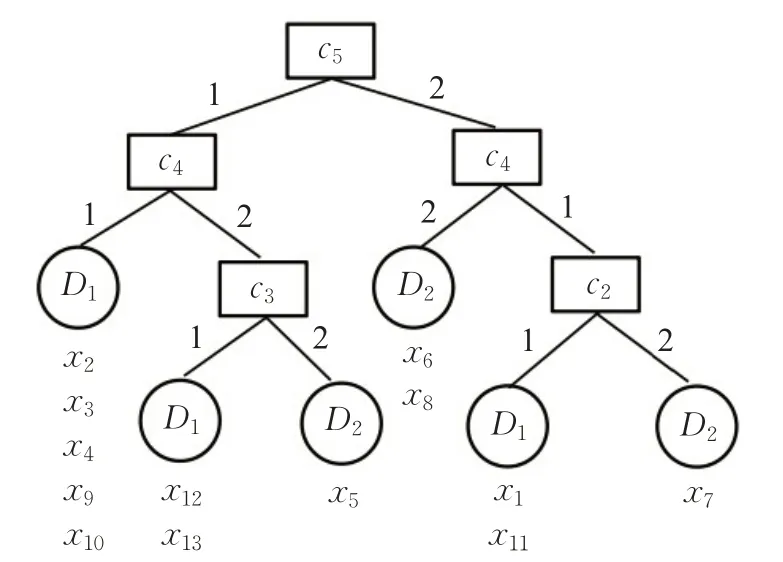
图2 基于IGGI算法的实例决策树Fig.2 Decision tree of example based on IGGI algorithm

3 数据实验验证

最后实施相关数据实验，验证IGGI算法对比于ID3算法与CART算法的有效性与先进性。为此，从UCI机器学习数据库（http：//archive.ics.uci.edu/ml）[18]中抽取6个数据集，具体信息参见表4。在实验中，首先进行数据预处理（包括删除具有缺失值的样本，进行连续数据的等距划分离散化），然后计算属性增链上的三种度量，最后实施三种决策树算法。

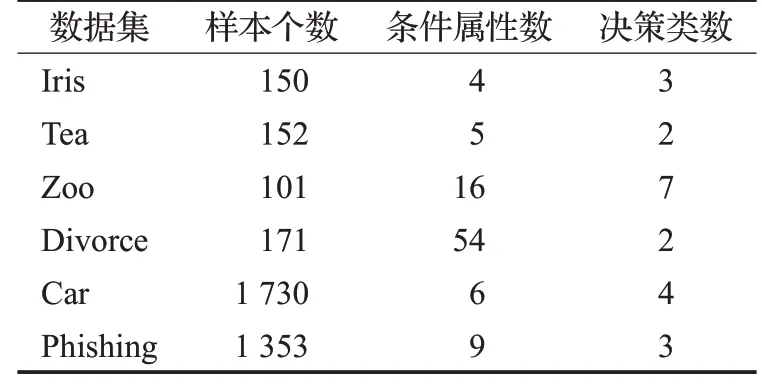
表4 实验数据集Table 4 Experimental data sets

对于自然属性增链（式（1）），相关的三种度量值描绘于图3，其中数据集Divorce在属性增链第7节点上就呈现度量最值，故只给了前面部分。由此可见引理1与命题1、命题2的理论结果。在增链方向上，信息增益是单增的，基尼指数是非单增的，两种度量是非线性相关的，而数据集Iris在(A2,A3,A4)以及数据集Zoo在(A12,A13,A14)的局部振动能够有效说明IgGi混合度量的粒化非单调性。

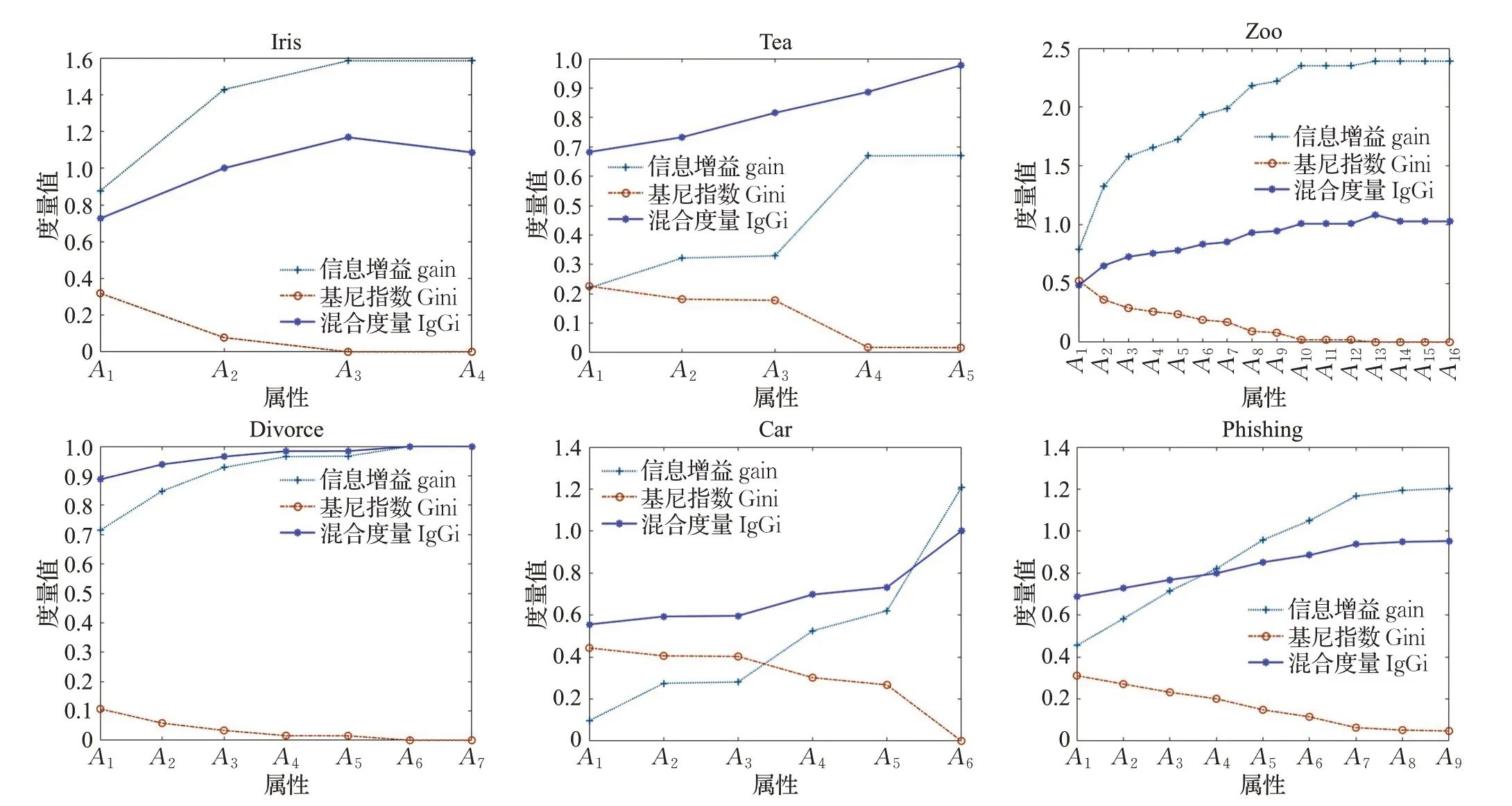
图3 基于属性增链的三种度量变化（实验）Fig.3 Three kinds of measure changes based on attribute-increase chain（Experiment）

在决策树实验中，将数据集均分为10份，随机选择9份作为训练集，1份作为测试集，进行十折交叉法验证。三种算法的最终结果如表5与图4（其中符号√标记最优值），这里关注“准确度”与“叶子数”两种经典评估指标。

基于表5与图4结果，下面对比分析ID3、CART、IGGI三种算法，从而揭示IGGI算法的相关优势。首先，考虑决策树准确度这一主要指标。在Tea、Zoo、Divorce、Car四个数据集中，IGGI算法的准确度高于其他两种算法；在Phishing数据集中，IGGI算法和ID3算法准确度一样，同时达到最优；在Iris数据集中，IGGI的结果介于CART算法与ID3算法之间，取得次优业绩。可见，IGGI算法在大部分数据集上满足准确性最优。其次，考虑叶子数这一结构指标。在Car数据集中，IGGI算法的叶子数最少，故优于其他两种算法；在Iris、Zoo两个数据集中，IGGI算法取得次优叶子数；在Tea、Divorce、Phishing三个数据集中，IGGI算法的叶子数和其他两种算法的差异并不大。对比于ID3与CART，IGGI算法在叶子数上具有最优、次优优势，且靠后时没有显著性劣势。最后，可以综合六个数据集计算结果，提供相关的统计分析；IGGI算法具有最优准确度，而其平均叶子数196对比于最优的177是可以接受的。综上，IGGI算法采用深入的度量集成与信息融合，从而追求与获取主要的决策树分类准确性，相关的计算与结果都是有效的，且一般优于ID3算法与CART算法，因此具有更强的适用性。

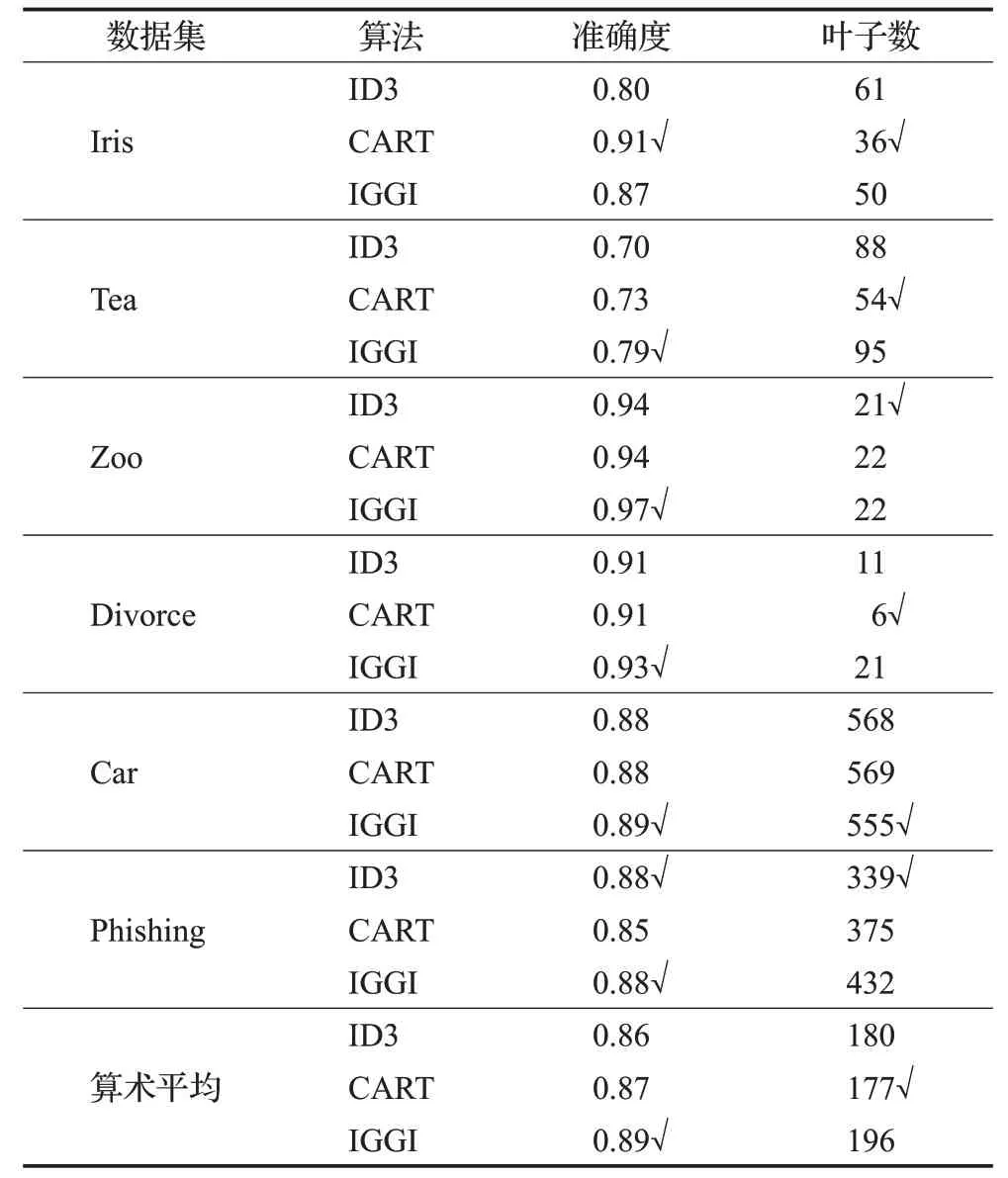
表5 三种决策树算法的实验结果对比表Table 5 Comparative table of experiment results of three decision tree algorithms

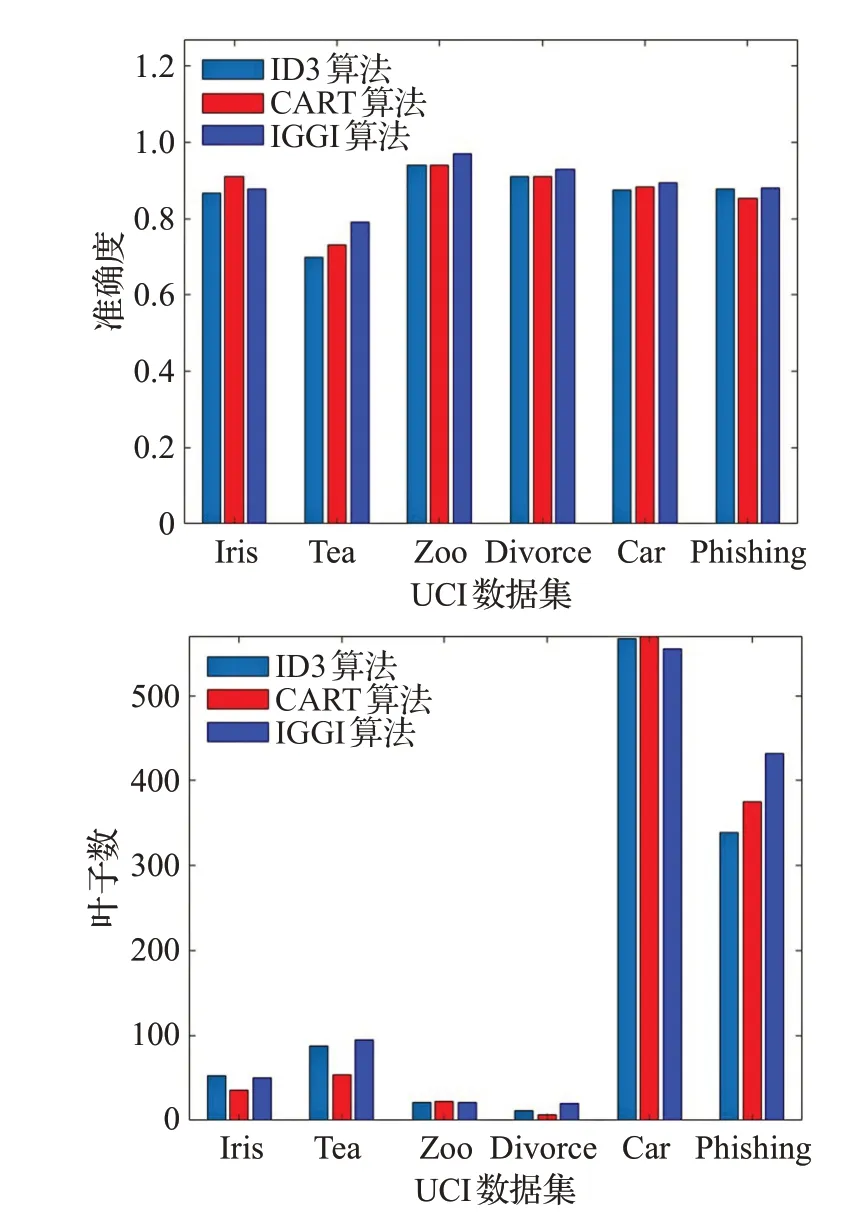
图4 三种决策树算法的实验结果对比图Fig.4 Comparative figure of experiment results of three decision tree algorithms

4 结束语

决策树算法主要依赖于不确定性度量构建，如ID3算法来源于信息增益而CART算法来源于基尼指数。本文集成信息增益与基尼指数来深入构造IgGi融合度量，进而设计了决策树分类的IGGI算法。基于理论研究与实验结果，IgGi度量与IGGI算法具有创新性、可行性、有效性；特别地，IGGI算法改进了经典的ID3算法与CART算法，具有更好的环境适应与分类业绩。接下来，IgGi度量还可以考虑结合其他不确定性度量（如属性依赖度），从而进一步提升IGGI算法的应用空间。