基于数值模拟方法的溢洪道设计
赵国强
(中工武大设计集团有限公司 新疆分公司,乌鲁木齐 830000)
0 引 言
为了宣泄水库多余的水量,防止洪水漫坝失事,确保工程安全,以及满足放空水库和防洪调节等要求,在水利枢纽中一般都设有泄水建筑物。常用的泄水建筑物有深式泄水建筑物(包括坝身泄水孔、水工隧洞、坝下涵管等)和溢洪道(包括河岸溢洪道、河床溢洪道)。由于提供高效输送水力和结构坚固的溢洪道对大坝的安全以及下游河流的生命和财产非常重要,因此在建造大型大坝时,应对溢洪道的水力稳定性进行设计分析[1]。
近年来,国内外通过室内试验和数值模拟手段对溢洪道的设计和水力性能进行了一系列研究。金辉杰[2]以落中子水电站为例,借助物理模型试验对比现状工况和优化工况的水流分布效果,优化了下溢洪道范围内流态;周望武[3]通过台阶溢洪道与锥形阀泄放管泄洪消能水工模型试验,论证了泄洪建筑物整体设计方案及下游消能防冲措施的合理性;张辉等[4]基于VOF法的RNGk-ε双方程紊流数学模型,对阶梯溢洪道水流压强特性及下游局部冲刷坑的形态和发展进行了三维数值模拟;张力鹏[5]以田家湾水库除险加固工程溢洪道陡槽续建为背景,通过水工模型试验进行溢洪道导流墙陡槽续建后溢洪道进口过流能力以及原工程段水面流态、流速与改建后溢洪道水面流态、流速的比较分析,并对溢洪道弯道段增加导流墙的优势进行总结; 武亚辉[6]采用二维水动力数学模型对某中型水库拟建溢洪道内的水流流态进行数值模拟,并利用设计方案中的成果进行模型计算结果复核,验证了该模型对溢洪道进行二维水动力数值模拟的可行性。
1 泄流量与数值假设
楔形砌块溢洪道最重要的一个设计步骤是估算通过相邻块体和孔口之间接缝的预期泄漏流量。其通常取决于3个参数:溢洪道的坡度、漫顶流量和砌块的大小。而砌块的大小又决定了每个表面单元的接缝长度。如果该排水流未能按设计流量排至下游坡脚,楔形砌块下侧会产生隆起,从而导致整个溢洪道不稳定,从而影响整个大坝的安全。
在本文的数值模型中,块体和接头被视为具有水头损失定律的连续介质,该方法广泛用于多孔材料渗流的数值模拟。其中,过水面积假设为整个断面面积,而不考虑管道的形状和分布或固体不渗透区域。本文采用式(1)中的固定水头损失定律,来模拟水流经多孔介质时发生的水头损失:
i=a·v
(1)
式中:i为水力梯度;a为渗透系数;v为渗透速度。
楔形砌块溢洪道可被视为具有接缝和孔口的管道,嵌入在固体和不透水基质(块体)中,因此整个渗透过程的水头损失定律可以通过式(1)进行描述。其中,系数a对于任何坡度和排水流量的溢洪道来说都是常数,只取决于块体的大小和形状,而块体的渗透性取决于接缝、孔口和块体组成的系统。
本次用于求解的有限元方法是根据固定网格的欧拉框架求解Navier-Stokes方程,通过添加水头损失定律作为耗散项进行修改,在微积分域中考虑多孔流体区域和非多孔流体区域。为了提高模拟效率,采用了基于边缘的方法和水平集技术来跟踪自由表面的演化。然而,由于采用正交子尺度稳定方法,因此没有模拟湍流情况。
2 水头损失定律验证
为了验证数值计算中上述水头损失定律的正确性,本文进行物理与数值试验对比分析。此次试验的溢洪道高度4.7 m,宽度0.5 m,下游坡度2∶1。流量设定为200和240 L/s,测得的渗透长度为6.5 m(32排)。本次建立的数值模型为3D模型,共划分650 000个四面体网格,楔形砌块的最大单元尺寸为0.01 m,其余计算域的最大单元尺寸为0.045 m。数值模拟时,先设置泄流流量为240 L/s,之后采用不同的渗透系数a进行模拟,最后将数值模拟中的泄漏流量与物理试验获得的泄漏流量进行比较。系数a值取两者结果之间差值达到2%以内时的值。本文中所校正的a值为8 400。图1为本次的物理与数值试验模型示意图。

图1 数值与物理试验模型
3 楔形砌块溢洪道设计步骤
渗流量的排水方式是设计楔形砌块溢洪道的一个关键方面,取决于大坝的类型。均质坝的坝体由不透水材料组成,因此必须铺设排水层以避免砌块底部的压力升高,使得整体具有足够的水力压力来驱动水流的渗透,保证坝趾而不受压力。同时,为了使砌块不受压力升高的影响,堆石料的渗透性必须使得块体底部与渗流网自由水面之间不发生接触。总体而言,楔形砌块溢洪道的设计必须确保砌块下没有可能影响其稳定性的水压。本文基于这一设计目标,根据大坝类型提出了一种设计办法。即设计一个挑坎,由一个混凝土框架组成,框架内填充多孔材料,用于分别驱动溢流和渗透流,同时还有助于支撑块体稳定。下面对整个楔形砌块溢洪道设计步骤进行详述,其中部分设计以之前的数值模拟得到排水试验为基础。主要设计步骤为:
1) 为防止大坝坡趾破坏引发滑坡,先计算饱和土坡的安全系数:
(2)
式中:Fr为坡体从坡趾滑动的安全系数;γe,sat为某一坝体材料的饱和容重;α为坡度;γw为水的容重;φ为摩擦角。
2) 根据宽顶堰流量方程计算导流堤的初始高度:
(3)
式中:q为单位泄流流量;Q为泄流总流量;B为溢洪道宽度;h为未考虑安全系数时导流墙的高度;hc0为考虑安全系数时导流墙高度;K为安全系数;g为重力加速度。
3) 计算坝趾高度:
(4)
其中:HT0为坝趾的初始高度;β为坝坡角,见图2。
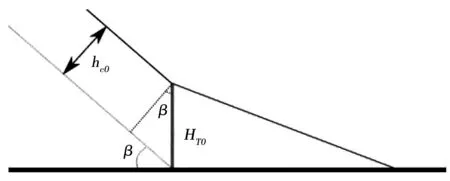
图2 各几何参数示意图
4) 计算相似系数:
(5)
式中:λ为相似因子;M为实际设计的块体质量;MB为获得渗流参数实验室测试的块体质量。
5) 更新坝趾高度:
(6)
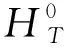
6) 更新导流墙高度(图3):
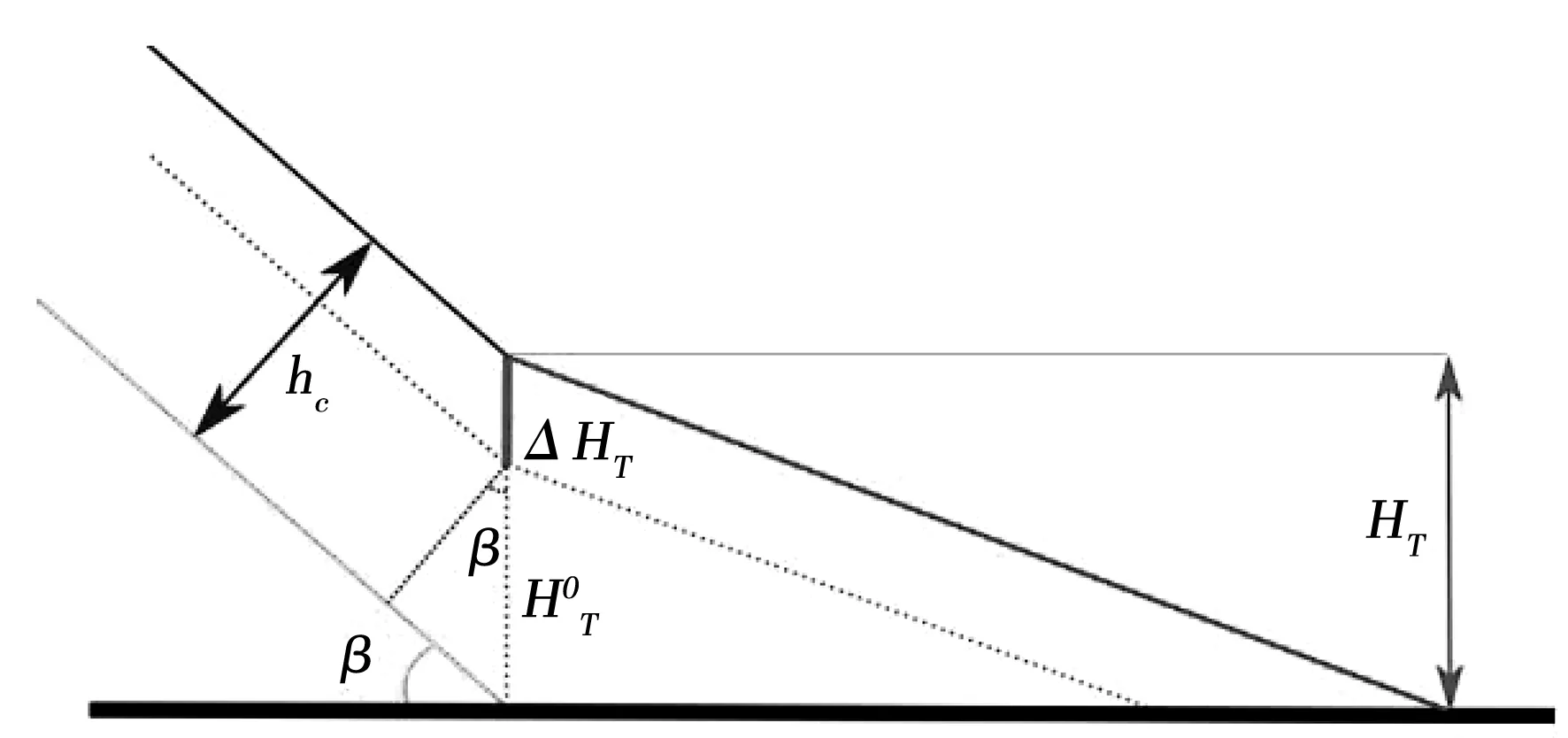
图3 更新后各几何参数示意图
hc=Ht·cosβ
(7)
在完成以上步骤后,根据设计方案计算渗流量。渗透流量取决于带砌块的衬砌区长度、坡度和砌块尺寸。该计算基于前一小节得到的数值试验结果。该试验结果可以用来训练一个神经网络,该网络允许在考虑的变化范围内计算任何坡度和流量组合的渗透流量估计值。这种方法避免了为每个坡度和流量组合拟合单独的表达式,并提供了中间值的估计值。此外,由于输入数据具有低噪声,因此训练过程简单明了。数值结果与神经网络估计值之间的最大差异为1.26%。这种方法与之前的工作中所采用的方法相同,即在数值模拟基础上获得计算闸门溢洪道流量的通用表达式,之后模拟坡脚和挑坎下的渗流考虑非线性阻力定律和检查饱和率。模拟坡脚和挑坎下的渗流中,如果以下表达式成立,则返回第(5)步,增加坡脚高度:
(8)
式中:GS为设计最大饱和率参考值;Ht为坝趾的高度;yt为挑流消能坎结构下的最大渗透高度。
如果不成立,继续检验以下表达式:
(9)
其中:yp为进入坝体的最大渗流高度,如果表达式成立,则返回第(5)步,增加坡脚高度;如果不成立则考虑非线性阻力规律的排水层渗流模拟及饱和率和抗滑稳定性验算(只适用于均质大坝)。如果下面式(10)成立,则增加排水厚度,直到表达式不成立:
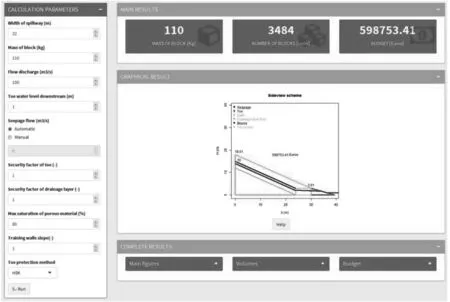
GS (10) 其中:GS为最大饱和速率输入,S为排水层饱和百分比。 之后计算排水层安全系数,不断增加排水厚度,直到达到安全系数值,计算式如下: (11) 式中:Fd为排水层安全系数;yd为进入排水层渗流高度;AB为测试时混凝土块长获得入渗数据;BB为测试块交叉长度。 在安全系数满足后,计算坝趾高度与排水层厚度之间的关系,如果式(12)为真,则返回步骤(5)增加坝趾高度: Ht>et·cos(β) (12) 式中:et为排水层厚度;β为坝坡角;Ht为坝趾高。 若坝趾与排水层厚度关系验证完毕后,计算抛填碎石直径,可采用Knauss表达式: (13) 其中:qi为渗流速度;α坝趾坡度;g为重力加速度,drr为抛填碎石平均直径。 最后,可根据现场实际情况计算材料的体积和最终预算。图4为基于R语言设计的自动化计算程序设计界面。该程序设计可以快速地对溢洪道设计的整个步骤进行寻优,允许在几秒钟内找到设计解,从一系列区块中找到一个最优经济解,并且得出最优预算解。 图4 基于R语言设计的自动化计算程序设计界面 本文提出了一种基于渗流数值模拟的楔形砌块溢洪道设计方法。首先将物理实验与根据欧拉框架求解Navier-Stokes方程的有限元结果进行对比,验证了不同流量下水头损失结果的一致性;之后基于该结果,对楔形砌块溢洪道设计步骤进行了详细叙述。整个设计方法过程包括溢洪道几何形状的不断修改、安全系数的验证、大坝抗滑性稳定性的验算。结论如下: 1) 本文提出的水头损失定律可以用于楔形砌块溢洪道的数值模拟当中,通过数值模拟中的泄漏流量与物理试验获得的泄漏流量进行比较,两者结果之间差值达到2%以内时的渗透系数取8 400较为合理。 2) 本文提出的设计步骤采用计算机交互式设计,基于R语言可对其进行迭代算法编程。结果验证,该算法允许在几秒钟内找到设计解,从一系列区块中找到一个最优经济解,能够简化和推广楔形砌块溢洪道的设计。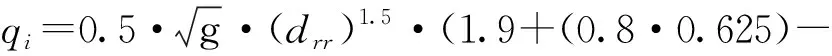
4 结 论

