基于SVMs-GA模型的微灌系统管网优化设计

刘 颖，郑荣伟，齐艳芳，陈宏彩

(1.浙江同济科技职业学院 基础教学部，杭州 311231； 2.浙江同济科技职业学院 教务处，杭州 311231；3.廊坊师范学院 理学院，河北 廊坊 065000； 4.河北省科学院 应用数学研究所，石家庄 050081；5.河北省信息安全认证技术创新中心，石家庄 050081)

1 研究背景

高效节水灌溉方式不仅可以提高水资源的利用率，还可以转变农业生产发展方式，是创建节水型社会的重要途径，也是目前破解农业生产用水瓶颈的主要方式[1]。高效节水灌溉需要动能设备和管道材料，优化输水管网的设计可以提高节水的效益和效果[2]。微灌是高效节水灌溉方式的一种，其管网系统涉及到干管、支管和毛管，管网设计、管道压力等都十分复杂。本文选择管网中最小的组成部分——1条支管及其连接的毛管组成的灌溉区域即微灌灌水小区为研究对象，在满足灌水均匀、允许系统压力差等条件下研究支、毛管的最优组合。

国内外优化管网设计主要集中于研究压力差在支、毛管的最优分配比例，很多研究认为0.45∶0.55是最优比例[2]；支、毛管的长度和管径最优[3]、支、毛管的位置最优[4-5]等。但是压力差在支、毛管的最优比例至今没有定论，且最优比例会随着管网的不同布置形式发生变化[6]。李援农等[7-9]直接计算整个系统的压力差，不再区分支、毛管的压力差分配比例，但是在计算管材成本时，先分别计算不同管径的管材最优，然后再从中选择整体最优，显然这样不利于找到整体最优解；马朋辉等[10-11]在上述基础上又综合考虑了能耗成本。管网的运行成本非常复杂，主要包括耗水量、管材成本、建设成本和能耗成本等。耗水量与种植作物的种类、气候等有关系；建设成本和能耗成本具有时效性和地域性；作物收成与作物的种类、种植方式和市场规律等有关系，这些都无法统一衡量，因此本文仅对管网的管材成本进行讨论。

本文采用支持向量机(SVM)耦合遗传算法(GA)，利用支持向量机[12-13]提高遗传算法中初始种群和遗传算子的质量，避免遗传算法早熟、收敛速度慢和容易陷入局部最优解的缺点[14]，在保持种群多样性[15-16]的同时更快地向适应度高的方向进化。

2 微灌灌水小区管网模型的建立

2.1 模型概述

在整个灌水小区中，假设支、毛管围成一个规则的矩形，毛管单向铺设时形成“梳齿”形，毛管双向铺设时形成“丰”字形。毛管均匀连接在支管上，毛管的间距为支管的标准段长，由作物的耕种间距决定；灌水器均匀连接在毛管上，灌水器的间距为毛管的标准段长，由作物种类、种植形式、土壤地质和地形条件等决定，则支、毛管的长度为标准段长与段数的乘积。因此本文的问题转化为求解支、毛管的段数。毛管单向铺设时整个灌水小区管道铺设方式和管道中的流量如图1所示。当毛管双向铺设时，示意图与图1类似。根据上述假设条件，选取支、毛管的段数为决策变量，分别建立毛管单向铺设和双向铺设时不限定灌溉面积的单位面积管材成本最低的优化模型。

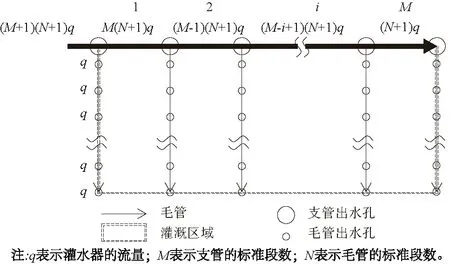
图1 毛管单向铺设时灌水小区管网、管道内流量、灌水器流量示意图Fig.1 Schematic diagram of pipe network, flow in pipe and flow of emitter in irrigation district when the lateral pipes are laid one direction

2.2 毛管单向铺设模型(模型Ⅰ)

2.2.1 目标函数

灌溉区域内的管材包括支管和毛管，其中支管由不同直径的管材构成，毛管由一种直径的管材构成，则支、毛管的总成本分别为：

(1)

(2)

式中：F1为支管的总成本(元/hm2)；a为可供选择的支管种类数；C1i为支管的单价(i=1,…,a)(元/m)；xi为第i种管径的支管的段数；m为每段支管的标准长度(m)；F2为毛管单向铺设时毛管的总成本(元/hm2)；C2为毛管的单价(元/m)；xa+1为毛管的段数；s1为支管到毛管上第一个灌水器之间的长度与每段毛管的标准长度的比例；n为毛管的标准段长(m)。

根据假设知灌溉区域为规则的矩形，所以支管的总长度和毛管的总长度分别构成了矩形的长和宽，则灌溉区域的面积为

(3)

式中As为毛管单向铺设时的灌溉面积(hm2)。

单位面积的管材成本最小为

(4)

式中Cs为毛管单向铺设时单位面积的管材成本(元/hm2)。

2.2.2 约束条件

2.2.2.1 压力约束

根据管道任意两孔口间的水头差[17-18]公式，得到整个管网上任两孔口间的水头差，上述水头差均应小于整个灌水小区允许的水头差，故有压力约束为

(5)

式中：ΔHkj为整个灌水小区第k个出水孔与第j个出水孔之间的水头差(m)；P为整个灌水小区所有的出水孔数；ΔHmax为灌水小区允许的最大水头差(m)。

2.2.2.2 非负整数约束和边界约束

决策变量为支管的标准段数，故为正整数型变量；灌溉区域为矩形，故支管、毛管的段数应≥1，因此非负整数约束和边界约束的数学表达式为

(6)

式中Z0+为正整数集。

2.3 毛管双向铺设模型(模型Ⅱ)

毛管双向铺模型与毛管单向铺设模型类似，因此模型的数学表示如下所述。

2.3.1 目标函数

毛管单向铺设模型目标函数为:

(8)

minCd=(F1+F3)/Ad。

(9)

式中：F3为毛管双向铺设时毛管的总成本(元/hm2)；xa+1为顺坡毛管的段数；xa+2为逆坡毛管的段数；s1为支管到顺坡的毛管第一个灌水器之间的长度与每段毛管的标准长度的比例；s2为支管到逆坡的毛管第一个灌水器之间的长度与每段毛管的标准长度的比例；Ad为毛管双向铺设时的灌溉面积(hm2)；Cd为毛管双向铺设时单位面积的管材成本(元/hm2)。

2.3.2 约束条件

与模型Ⅰ类似，毛管双向铺设时约束条件由压力约束、非负整数约束和边界约束构成，其中边界约束包括顺坡和逆坡两个方向的边界约束，具体见式(10)。

(10)

3 SVMs-GA算法

SVMs-GA算法首先把GA种群中的每一个个体视为向量，根据适应度的高低对个体进行多分类(SVMs)[19]，以此视为训练样本。利用SVMs算法构造适应度的判别器，在GA进化过程中，用构造好的判别器控制遗传算法中种群的选择、交叉和变异等进化算子，使种群在保持多样性的情况下，更快地向适应度高的方向进行搜索，具体流程见图2。

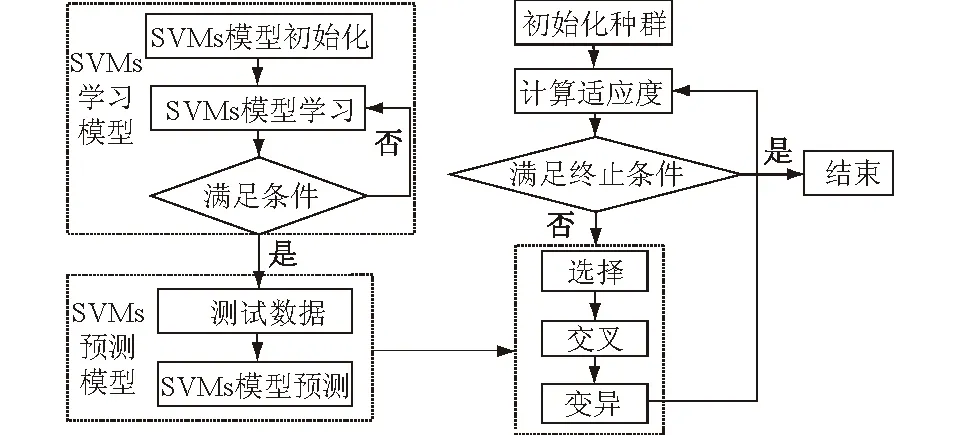
图2 SVMs-GA算法流程Fig.2 Flow chart of SVMs-GA algorithm

4 与已有文献的比较

本文选用文献[7]3.1节中的算例假设条件， 确定SVMs的Ⅰ、 Ⅱ、 Ⅲ类所属的区间分别为[0.9, 1]、[0.5, 0.9)和[0, 0.5)，以阈值0.8生成判别器。三类个体按照6∶3∶1的比例进行选择；交叉概率分别为0.2、0.5、0.9；变异概率分别为0.1、0.2、0.4；算法最大迭代次数为200，利用SVMs-GA对模型求解。

4.1 最优解的情况

利用上述算例数据和SVMs-GA算法的参数分别对模型Ⅰ和模型Ⅱ进行求解，并将求解结果和GA算法的求解结果进行对比，分别见表1和表2。

由表1可知，毛管单向铺设时，毛管的段数在22～25范围内取到最优解，由SVMs-GA算法得出的每公顷管材成本比文献[7]少了5%，灌溉面积比文献[7]增加了23%，同时本文还得出当毛管段数为25时，可以得到不错的最优解，且此时灌水面积比原来增加了近0.1 hm2。

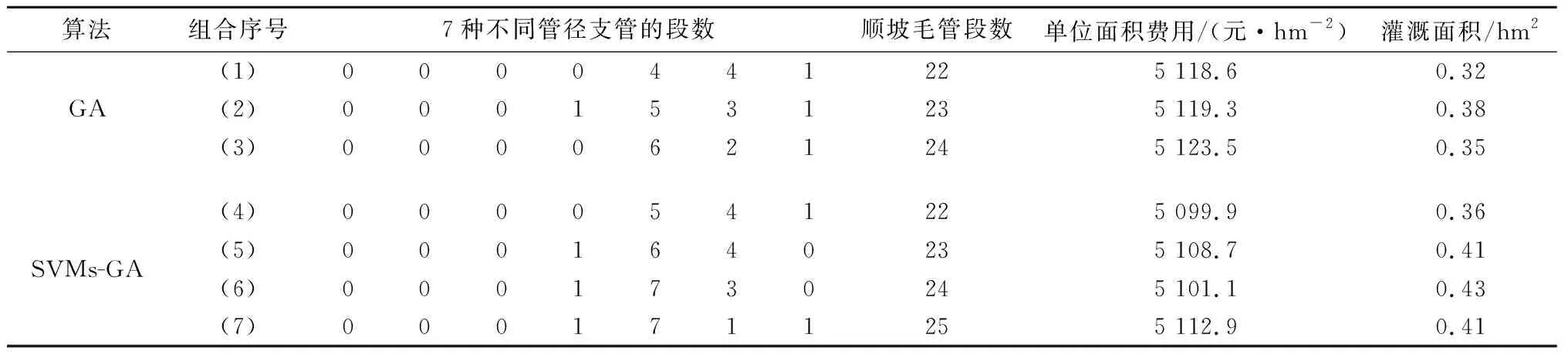
表1 毛管单向铺设时GA和SVMs-GA优化结果对比Table 1 Comparison of GA and SVMs-GA optimization results when the capillary is laid in one direction

由表2可知，毛管双向铺设时，顺坡和逆坡的毛管段数都在19～22范围内取到不错的最优解，由SVMs-GA算法得出的每公顷所有管道的单位面积成本比文献[7]少了5%，灌溉面积比文献[7]增加了20%，同时本文还得到当毛管顺坡和逆坡段数分别为22和21时，可以得到最优解，此时灌水面积与文献[7]相同。

表2 毛管双向铺设时GA优化结果和SVMs-GA优化结果对比Table 2 Comparison of GA optimization and SVMs-GA optimization results when the capillary is laid in two directions

4.2 可行域的情况

从图3可以看出，利用SVMs-GA算法计算出的最优组合中，在系统最大水头差为5.5 m的约束下，每一种组合的系统水头差均能达到5 m以上，且第(13)种组合的逆坡水头差达到了5.499 m，为系统允许的最大水头差的99.98%。说明SVMs-GA算法是在充分搜索了模型可行域的基础上取到的最优值。

图3 不同管径的管道最优组合的系统相对水头差Fig.3 System’s relative pressure difference of optimal combination of different pipe diameters

5 模型验证

以浙江省杭州市临安山核桃项目的高效节水灌溉模式为例，整个灌区面积为53.33 hm2，采用自压灌溉，灌区根据实际经验采用毛管双向铺设。微喷头流量为7.6 L/h，灌水小区允许的最大水头差为4.12 m，支管出水口间距为6 m，毛管滴头间距为6 m，支管距离毛管第1个滴头的距离为3 m，沿毛管布置方向地面坡度为0.001，沿支管布置方向地面坡度为0.05。可供选择的支管和毛管的相关参数见表3，其中单价以浙江省2020年9月份市场价为参考。

表3 可供选择的支管和毛管相关参数Table 3 Parameters of available branch and capillary

将上述数据代入模型Ⅰ和模型Ⅱ，利用SVMs-GA算法进行求解，结果见表4。

从表4可知，毛管双向铺设比毛管单向铺设管材单位面积的成本降低了6.5%，这与文献[7]—文献[9]和文献[20]的结果以及项目地区的经验铺设方式均一致。第(19)—第(22)的管网组合中灌溉面积为22.18～24.43 hm2，小于整个项目的灌溉面积53.33 hm2，因此符合模型不限定灌溉面积的假设。

2种铺设方式中，系统的水头差达到了允许的最大水头差的97.6%～99.7%，说明上述最优解是在充分搜索可行域的基础上得到的。

从表1、表2和表4可以看出，22种最优组合中，被选中的支管都集中在管径较小的几种支管，说明支管的管径越小，管材的单位面积成本越小。

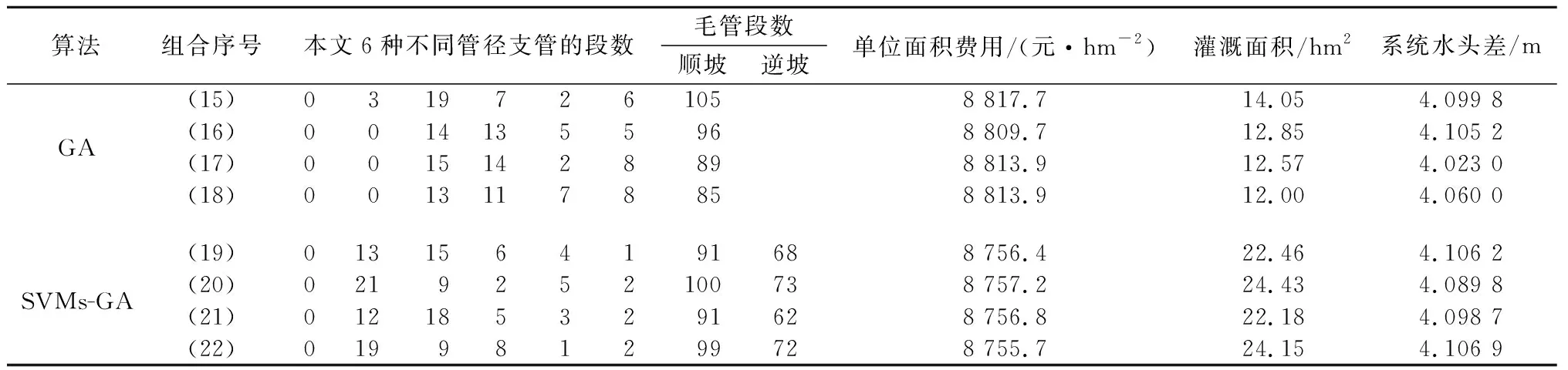
表4 山核桃项目管网优化组合方案Table 4 Optimal combination scheme of pipeline network in Carya cathayensis project

6 结 论

管材成本占微灌系统总成本的50%以上，因此优化管网设计对降低微灌系统总成本十分重要。本文以微灌管网的最小单元为研究对象，在不限定最大灌溉面积的前提下，对支、毛管的布置形式，不同直径的管材进行优化组合，利用SVMs-GA算法，在充分搜索可行域的基础上，得到单位面积管材成本的最优解，以及取到最优解时的灌溉面积。目前浙江省主推的经济型微喷灌中，单元小型化是经济型的基础，会遇到灌溉面积小于上述取到最优解时的灌溉面积，因此今后还需要对限定最大灌溉面积的情况进行研究。