基于时空网络的列车运行计划应急调整方法

段卿培， 冯小芳， 李欣

（1. 中国铁路北京局集团有限公司 调度所，北京 100860；2. 中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081；3. 北京经纬信息技术有限公司 铁路运输与调度技术中心，北京 100081）

0 引言

列车运行过程中会遇到一些外界因素干扰，无法按照计划运行，造成不同程度的晚点，如大风天气导致列车限速运行、设备故障导致区间封锁等。因此铁路运输组织除了需要制定列车运行计划，还需根据实际突发情况对列车运行计划进行相应调整。随着高速铁路的不断发展，繁忙干线上高速列车开行列数日益增长，当面临大规模扰动时，传统人工调整列车开行计划的方法使调度员面临高强度的工作挑战，且该调整方法也很难满足调度调整时效性的要求。

目前，列车运行计划调整问题的研究方法主要有：（1）基于规则的专家系统模式［1−2］；（2）基于遗传算法、模拟退火算法等智能优化算法模式［3−4］；（3）基于运筹学模型的模式，常用建模方式包括基于网络流建模［5−6］、基于替代图建模［7−8］等。鉴于网络流建模方法是针对每一列车建立独立的网络流模型，有助于区分不同等级列车，更符合我国高速铁路运输生产场景，在依照既有调度策略规律［9］的基础上，将以时空网络的网络流建模方式研究列车运行计划应急调整方法，使调度员能够快速、合理地制定调整计划，提高应急行车指挥的决策效率。

1 关键技术

1.1 时空网络

通过时空网络对时间、空间的离散化表示，构建列车所有可能时空轨迹的枚举（见图1）。网络中共有4 种节点：（1）虚拟起点，表示列车在时空网络中生成；（2）虚拟终点，表示列车在时空网络中消失；（3）到达节点，表示列车在某一时刻在车站进行到达作业；（4）出发节点，表示列车在某一时刻在车站进行出发作业。网络中共有4 种弧段：（1）虚拟起始弧，表示列车驶入时空网络表示的时空范围；（2）虚拟终止弧，表示列车驶出时空网络表示的时空范围；（3）站内停站（通过）弧，表示列车在某一车站从到达作业向出发作业的转变，可分为列车停站和列车通过；（4）站间运行弧，表示列车在区间运行。

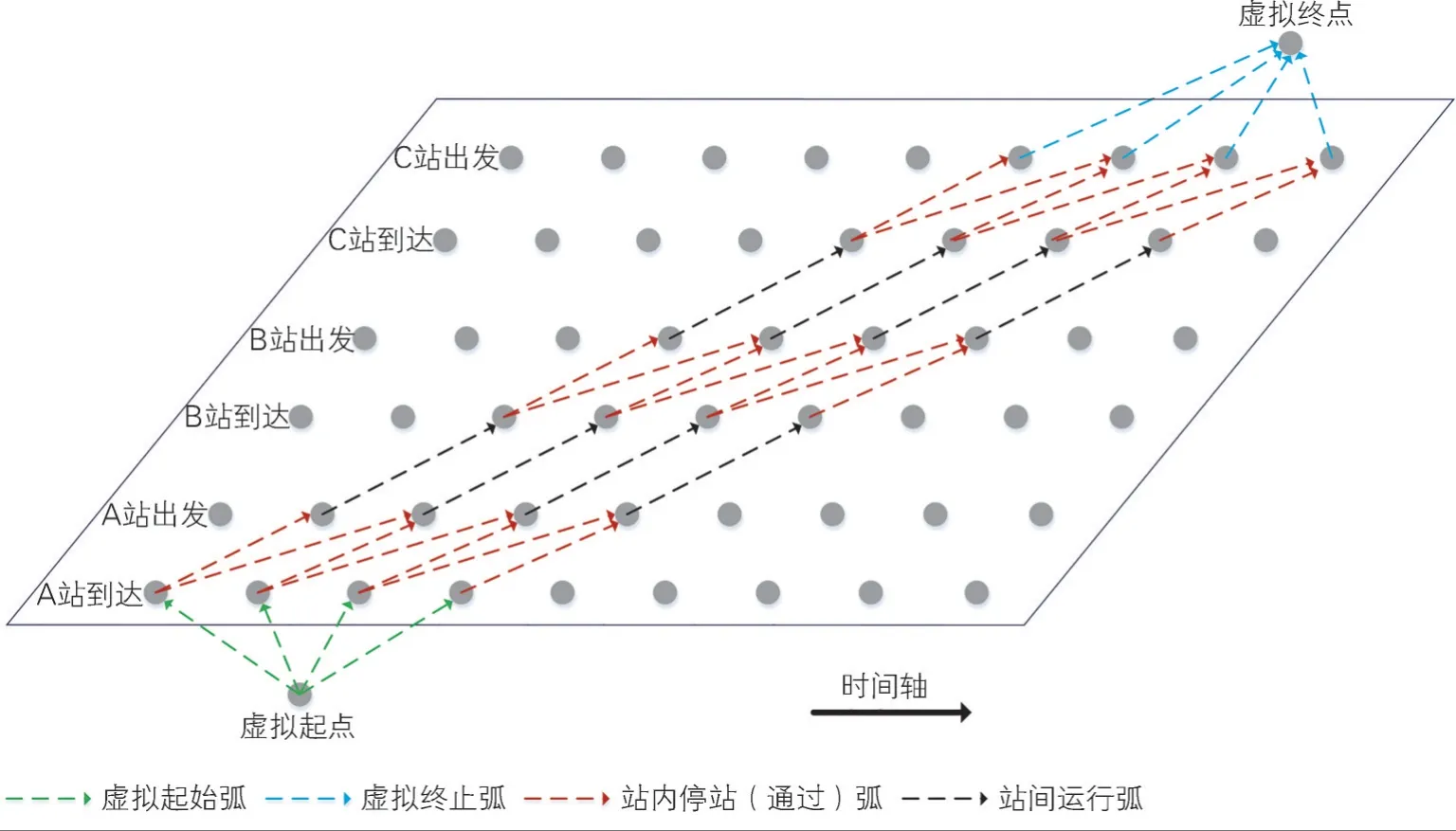
图1 时空网络示意图

在图1构建的时空网络中，节点和弧线需要满足问题约束和临时限速（封锁）命令限制，因此构建模型时，各节点和弧线需满足：（1）站间运行弧的运行时间不得小于运行时分标尺；（2）不得在列车原计划停站车站建立站内通过弧；（3）所有站内停站弧的停站时间不得小于车站最小停站时分；（4）在临时封锁命令的时空范围内不得有站间运行弧；（5）列车出发时间范围应考虑车底接续关系。其中（5）具体指：具有车底接续关系的列车，在折返站应满足最小折返作业时间要求［10］。另外，为了限制时空网络的网络规模，还需设置列车在首站的出发时间范围和沿途各站的最大作业时间。通过逐一枚举满足以上约束的时空路径，得到各列车的时空网络。由于实际运输生产环境中列车等级不同、列车停站方案不同、临时限速（封锁）命令对列车的影响范围不同，因此时空网络应参照各列车的区间运行时分标尺、技术作业时间标准、停站方案、受临时封锁（限速）的影响范围，针对每一列车构建时空网络。

时空网络中，每条弧线上占用一定数量的时空点表示列车运行过程中对股道的占用，这些时空点也被称为“时空资源”［6，11］，通过约束各时空资源至多被1列车占用的策略，保证列车间的追踪间隔时间。约束时空资源需首先定义车站“行车资源”。将车站离散为接车进路、到发线、正线和发车进路4 种类型，这4 种类型线路被称为行车资源（见图2），列车通过车站时需占用行车资源。将行车资源沿时间轴展开，得到时空资源。按对应的行车资源类别，时空资源也可分为接车时空资源、发车时空资源、股道时空资源。站间运行弧会占用发车时空资源和接车时空资源，站内停站（通过）弧会占用股道时空资源。各弧段行车资源占用的时间范围可根据最小间隔时间标准得到。由于在实际调度调整过程中，采用的最小间隔时间标准可能与编制列车运行图所采用的间隔时间标准不一致，在此所指的所有间隔时间均指调度调整中所采用的间隔时间标准。以到达间隔时间为例（见图3），最小到达间隔时间和最小到通间隔时间可分为2 部分：前车延后释放时间、后车提前占用时间。其中延后释放时间指从列车车头到达接车进路起，至接车进路解锁为止的时间。提前占用时间是指从接车进路开始办理，至列车车头到达接车进路为止的时间。发车进路占用时间范围与接车进路类似。对于到发线和股道，其占用时间范围等同于列车停留（通过）股道时长。

图2 车站“行车资源”

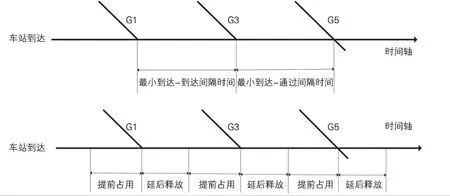
图3 最小到达间隔与占用“时空资源”转换

1.2 多商品流模型

在时空网络中，列车运行线就是1条由节点和边顺序衔接的路径，运行调整问题就是为每一列车分配1条与其他列车没有冲突关系的路径。若将1 列车视为1 支网络流，则运行调整问题可归结为时空网络上的多商品流问题［12−13］。在此基础上可构建列车运行调整问题的模型，模型参数见表1。

表1 模型参数

具体模型定义如下：式（1）表示目标函数，即总晚点时分最小。假设列车到达s点（或驶离s点）的计划时刻为t0，则|t0−t|；式（2）为流平衡约束；式（3）标记了各列车时空网络中每条时空弧所占用的时空资源；式（4）标记了列车对各时空资源占用的约束；式（5）表示任意时空资源最多只能被1列车占用。当1时，就会出现列车冲突；式（6）为决策变量的取值约束。

1.3 拉格朗日松弛算法

制约上述模型求解效率的约束是约束（5）（即式（5）），它导致各列车之间产生了大规模的组合优化，进而影响求解速度。拉格朗日松弛是处理这种组合优化问题的常用方法，它将复杂约束松弛，并将其构造为惩罚项加入目标函数中，形成拉格朗日对偶问题，从而使得原本的组合优化问题转变为针对单一个体的优化问题，降低了模型求解难度，在此采用拉格朗日松弛算法解决求解效率问题。

首先将约束（5）松弛，利用拉格朗日乘子λrs，t，构造拉格朗日对偶问题Z(D)，Z(D)的目标函数为：

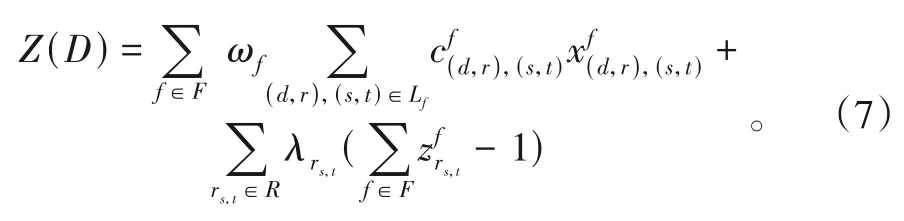
对式（7）进行恒等变换，得：

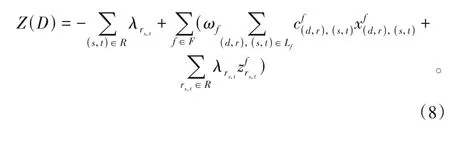
为使拉格朗日对偶问题的解逼近原问题的最优解，需要迭代更新拉格朗日乘子的值。采用次梯度法更新拉格朗日乘子：

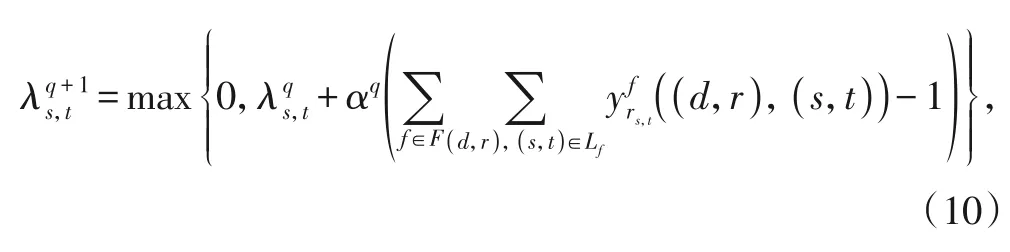
式中：q表示当前迭代次数，

一般情况下，拉格朗日对偶问题计算得到的是不可行解，还需利用启发式算法对结果进行可行化。当迭代结束后，由于拉格朗日乘子λrs，t实际上代表违背约束（5）的惩罚值，即λrs，t越大，各列车子问题求解结果在(s，t)处的冲突越大。利用式（11）可以计算列车f总冲突值CVf。

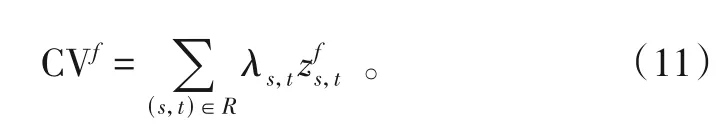
计算完毕后对各列车CVf进行排序，CVf越大代表该列车产生冲突越严重，应当在调整中优先铺画。各列车依次铺画完毕后，即得到1个可行解。

相应的拉格朗日算法，输入为模型相关输入；输出为对偶问题的解、原问题可行解。具体求解步骤如下：

步骤1：初始化。

步骤2：求解对偶问题。（1）利用最短路径算法求解拉格朗日对偶问题；（2）求解对偶问题最优解下界。

步骤3：将对偶解转换为可行解，采用基于优先级规则的实现算法将对偶解转换为可行解，并计算对偶问题最优解上界。

步骤4：计算最优解上下界的最优偏差。

步骤5：更新拉格朗日乘子。

步骤6：迭代结束条件。

2 实现方法

基于以上关键技术做后台算法支撑，设计研发了列车运行计划应急调度调整原型系统，并给出具体算例作为测试用例，借助系统直观体现调整结果，通过系统结果分析验证基于时空网络的列车运行计划应急调整方法的效果。

2.1 原型系统

系统前端基于apache tomcat 架构，采用Java 开发语言；后端基于.net framework 4.0 框架，采用C#开发语言。系统主界面见图4，可以设置故障线路、故障区间、线路封锁行别、线路封锁时间范围等选项，同时可实现调整计划发布、调整计划导出等功能。点击“运行图”按钮，可跳转至自动调整结果展示界面，通过列车运行图方式显示所有车次调整后的运行计划和正晚点情况，可分别选择不同线路行别查看，同时可以在调整结果展示界面进行人工手动调整，用户可根据实际需求调整列车运行计划。并根据晚点时长差异，分红、黄、绿3 色站址运行线（见图5）。

图4 系统主界面

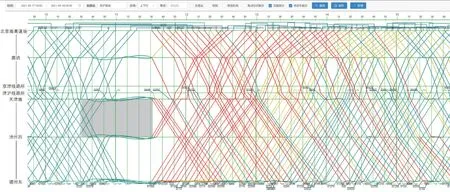
图5 调整结果展示界面及手动调整界面

2.2 算法示例

算例以京广高铁为背景构造，共包含中国铁路北京局集团有限公司管内的北京西—安阳东共12 个车站和1个线路所。本算例模拟的运输场景为：模拟徐水东站—保定东站的上行和下行区间均被临时封锁场景，模拟封锁从12：05 开始至14：05 结束。按照上述模型和算法调整后的运行图结果见图6、图7。该算例在CPU 为Intel（R）i7−10750H、内存为16G 运行环境下的优化结果见表2。

表2 算例优化结果

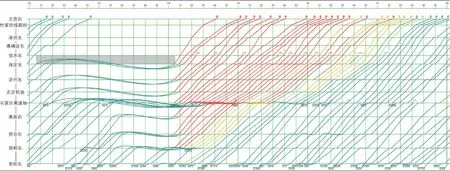
图6 优化后上行方向列车运行图

图7 优化后下行方向列车运行图

2.3 结果分析

算例求解结果中，下行方向晚点时长更长，这是由于北京西站属于折返站，大部分下行列车需依赖上行列车的车底进行作业，因此算例中下行列车发车时间范围还受到上行列车晚点的影响，晚点时长更长。

另一方面，在为各列车的时空网络划定封锁区间影响时空范围时，不仅包含徐水东站—保定东站的封锁区间，还考虑到实际现场运输指挥时，调度员通常不允许临时封锁结束时间前对车站扣车提前发车，因此在图6、图7 中，各车站在封锁时间内的扣车均未提前发车。

3 结束语

从算例求解效果看，上述基于时空网络的列车运行计划应急调整方法的模型和算法以及依此设计的列车运行计划自动调整系统，能够适应实际运输生产场景的准确性和时效性要求，对实际应急调度指挥工作具有一定指导作用，并有助于减轻调度员工作强度。