浅谈高中物理资优生能力培养
——以物理竞赛与大学先修能力要求为例
周金旺(柳州高级中学 广西 柳州 545006)
教育强国需要高中阶段就要培养更多的拔尖创新人才,示范性高中由于生源的优势将更加需要培养更多资优生.我校作为示范性高中一直致力于资优生的培养.物理学科除了正常开设全国统一的新课标课程外,还开设了物理类校本选修课程.对于物理类资优生来说主要是选修高中物理竞赛课程和中国大学先修(CAP)物理力学,而这两种课程的能力要求是不同的,高中物理竞赛是对高中的物理知识利用数学的方法进行综合分析,而大学先修物理力学课程主要是利用高等数学的知识来研究物理原理、解决物理问题,要求学生学习导数、数列极限、微积分、微分方程求解等数学知识.
本文以两个物理经典问题求解为例,来对比分析高中物理竞赛与大学先修物理力学的对能力要求所存在的区别.
1 求解绳子端点物体的速度和加速度
【问题1】如图1所示,一个人拉着轻绳的一端在水平面上以速度v0匀速向右前进,轻绳的另一端跨过定滑轮连接一重物B,不计定滑轮的质量与摩擦力,定滑轮的最高点与轻绳末端的竖直高度为h,求:当绳子与水平面夹角为θ时,重物B上升的速度和加速度的大小.

图1 问题1图示
1.1 高中物理竞赛能力要求
重物B上升的速度即绳子移动的速度,对绳子末端A的速度进行分解,如图2所示,得v=v∥=v0cosθ,如图3所示,以O点为参照系.

图2 绳端速度分解
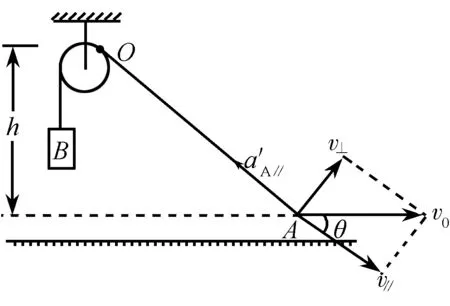
图3 O点的建立与加速度方向
绳子末端A绕O点以线速度v⊥做圆周运动,该圆周运动的加速度aAO记为a′A,沿绳子方向,即向心加速度,其大小为
以地面为参照系,根据参考系加速度变换得出A的加速度的矢量式
aA地=aAO+aO地
即
将这个矢量式分解到沿绳子方向的分矢量为
其中aO∥=aB,由于A在水平方向匀速前进,所以aA地=0,aA∥=0,得到重物B的加速度大小
以上是高中物理竞赛的能力要求,涉及到的知识点有相对速度、相对加速度的转换,速度的合成与分解,以及曲线运动中加速度计算.如果是用大学先修的物理知识,也就是主要用高等数学的相关方法来解决问题,方法如下.
1.2 大学先修物理力学能力要求


图4 直角坐标系的建立
所以重物B的加速度
以上是用大学先修物理力学的指导方法[1,2],从数学的角度建立坐标系,再利用高等数学中求导数的知识解决物理实际问题.
2 求解交叉点物体的速度和加速度
【问题2】如图5所示,水平直杆AB在半径为R的固定圆环上以速度v0匀速竖直向下运动,当运动到半径与竖直方向的角度为θ时,试求套在该直杆和圆环的交点处小环M的速度和加速度.

图5 问题2图示
2.1 高中物理竞赛能力要求


图6 小环M速度分解
再求交点处小环M的加速度,由于小环M沿圆环做圆周运动,设其法向加速度为an,则
切向加速度为aτ,由于直杆AB杆是匀速运动,在垂直于AB方向的加速度为零,如图7所示,则有

图7 小环M加速度分解
ancosθ-aτsinθ=0
解得
小环M的加速度只能是沿着AB方向,有
方向沿杆由B指向A[3].
2.2 大学先修物理力学能力要求
y方向的分速度
vMy=v0

图8 直角坐标系的建立
x方向的分加速度
负号表示方向.y方向的分加速度
方向沿杆由B指向A.
3 结束语
求解速度和加速度都是物理力学中常见的一类问题.本文以两个经典物理问题为例,依次采用物理竞赛的思想和方法以及采用大学先修物理力学的方法求解,得到相同的结果.通过对比分析,高中物理竞赛的能力要求主要是在利用高中物理的知识来建模求解,而大学先修物理力学课程对高等数学的要求较高.对于运动学和力学中的常见问题,通常都是建立恰当的直角坐标系后,坐标的变化与位移的变化相对应,利用对位移(坐标)的一阶导数求出速度,对速度求导得加速度,即位移的二阶导数求得加速度.也就是说对高等数学的能力提出了更高的要求,特别是导数、数列极限、微积分、微分方程的求解等,高中教师在指导物理资优生学生提高学科素养时要注意到两者的区别.

